-2. 解説放送
こちらの記事の解説放送です。
https://www.youtube.com/watch?v=-DbQqP7iZSE
-1. 私は誰?
秋田で
- 群知能(おそらくメイン)
- 競技プログラミング(趣味)
- DeepLearning(来年からやりそう)
を主に研究している学生のガナリヤです。
環境構築・プログラミング言語の理解を苦手としています。
随時更新していきます!
0. はじめに
群知能という最適化分野は、海外だとメジャーですが、日本ではかなり影が薄い分野です(工学系の方が多いので数理最適化などが多いのかもしれません)。
このままだと寂しいので(もっと流行って欲しい)、今回は、群知能のメジャーなフレームワークACOについてまとめようと思います。
僕はまだまだ群知能に関しても、Pythonに関してもプログラミングに関しても技術が未熟です。
ぜひ、わからない点や、ソースコードに変なところがありましたら、コメントをいただけるとありがたいです!
1. アントコロニー最適化とは?
アントコロニー最適化とは、現実の蟻の群れの行動に着目した組み合わせ問題の最適化手法です。
現実の蟻の群れは集団で行動し、巣から餌までの最短経路を発見できます。
これらの性質に着目したmarco dorigo氏が、プログラム上のシミュレーションで蟻の行動を模倣し、巡回セールスマン問題の優良解を発見したのがACOの始まりとなっています。
アントコロニー最適化は、英語だとAnt Colony Optimization(ACO)と呼ばれ、その名の通り最適化問題の最適値を小さい計算量でできるだけ良い解を求めよう!というものです。
アントコロニー最適化が適用される問題としては
- 巡回セールスマン問題
- 輸送問題
- 最小全域木
- 最小集合被覆
- Webクローラ
などなど、多くの適用できる問題があり、すべてグラフネットワークに帰結できる、という共通点があります。
2. 現実の蟻の特徴は?
まず、プログラム上のACOに入る前に、現実の蟻の特徴について考えてみましょう。
2-1. 群れで最短経路を発見する
現実の蟻は、群れで行動します。
蟻は、嬢王蟻と働き蟻に分かれていて、働き蟻がすべての業務を行っているのはご存知だと思います。
この働き蟻たちは、巣をさらに繁栄させるために、餌を巣から探しに行く必要があります。例えば、近くに落ちている昆虫の死骸を運んだり、もしくは他の昆虫と戦って殺してから死骸を運んだりします。
ここで、疑問になるのがどうやって蟻は餌を見つけているのでしょうか?
蟻たちは、人間とは異なり、声を出すこともできません。当然ハンドサインや、電話も使うことができません。
それにも関わらず、巣から餌までの最短経路を発見し、効率良く餌を巣まで運ぶことができます。
実は、蟻たちは人間には見えないフェロモンという情報を自分が通った経路に分泌しながら、餌を運びます。
すると、蟻はフェロモンの強い・より溜まっている経路を選択しやすい性質があるため、より多くの蟻が往復する最短経路に蟻が集まり、結果として蟻たちは直接意思疎通することなく、最短経路を効率良く発見することができます。
この、「直接意思疎通は取らないが、フェロモンを環境に分泌し、環境のフェロモンを知覚することで意思疎通を取る」という性質を、シミュレーションにしたのがACOとなっています。
2-2. 非常に馬鹿だが賢い
このように、蟻たちは群れでもっともフェロモンがよく貯まる最短経路をすばやく効率的に発見することができ、非常に賢いです。
しかし、これはある意味嘘であり、1匹1匹それぞれの蟻は非常に頭が悪いです。
というのも、蟻は非常に頭の容量が小さく、フェロモンの強い方向により進みます。
非常にシンプルな行動しか行なえません。
そのため、偶然、蟻たちがまん丸にお互いがお互いを追いかけるようにフェロモンを分泌してしまうと、それぞれが最短経路だと勘違いし続けてフェロモンが円形に溜まってしまい、そのまま永遠と回り続けた挙げ句死んでしまいます。
このように確かに蟻の群れは賢いですが、蟻それぞれは非常にシンプルなルールでしか動いていないため、ある意味バカであるといえます。
「群れだと賢いが、各個体はシンプルなルールで動いている」、というのは群知能の大事な特徴となっています。
これによって、組み合わせ問題が複雑になったり、スケールが大きくなっても、各エージェントはシンプルだが、群れとして最適化を行うことができ、汎用的に最適値を求めることができます。
3. ACOのイメージは?
これまで見てきたように、蟻は最短経路を群れとしてフェロモンを媒介とすることで発見しています。
この特徴を、グラフネットワークにおいて、シミュレーション化したものがACOとなっています。
3-1. グラフネットワークにモデリング
コンピュータ上でのシミュレーションを行うために、ACOを適用する前に組み合わせ問題を、必ずグラフネットワークに置き換えます。
グラフネットワークの頂点の数が$V$, 辺の数が$E$とし、このグラフを$G=(V, E)$と表すこととします。
また、頂点$(i, j)$を結ぶ辺を移動するのにかかる時間を$w_{i, j}$と表すこととします。$t$を移動開始してからの経過時間とします。
例えば、巣である頂点$1$から、餌の頂点$4$までの最短経路を見つける、ということをしばらく考えてみましょう。
(普通は、NP困難な組み合わせ最適化問題として名高いTSP問題をACOでは基準としますが、まずは簡単な最短経路発見問題を考えてみます。)
3-2. 蟻の確率的選択
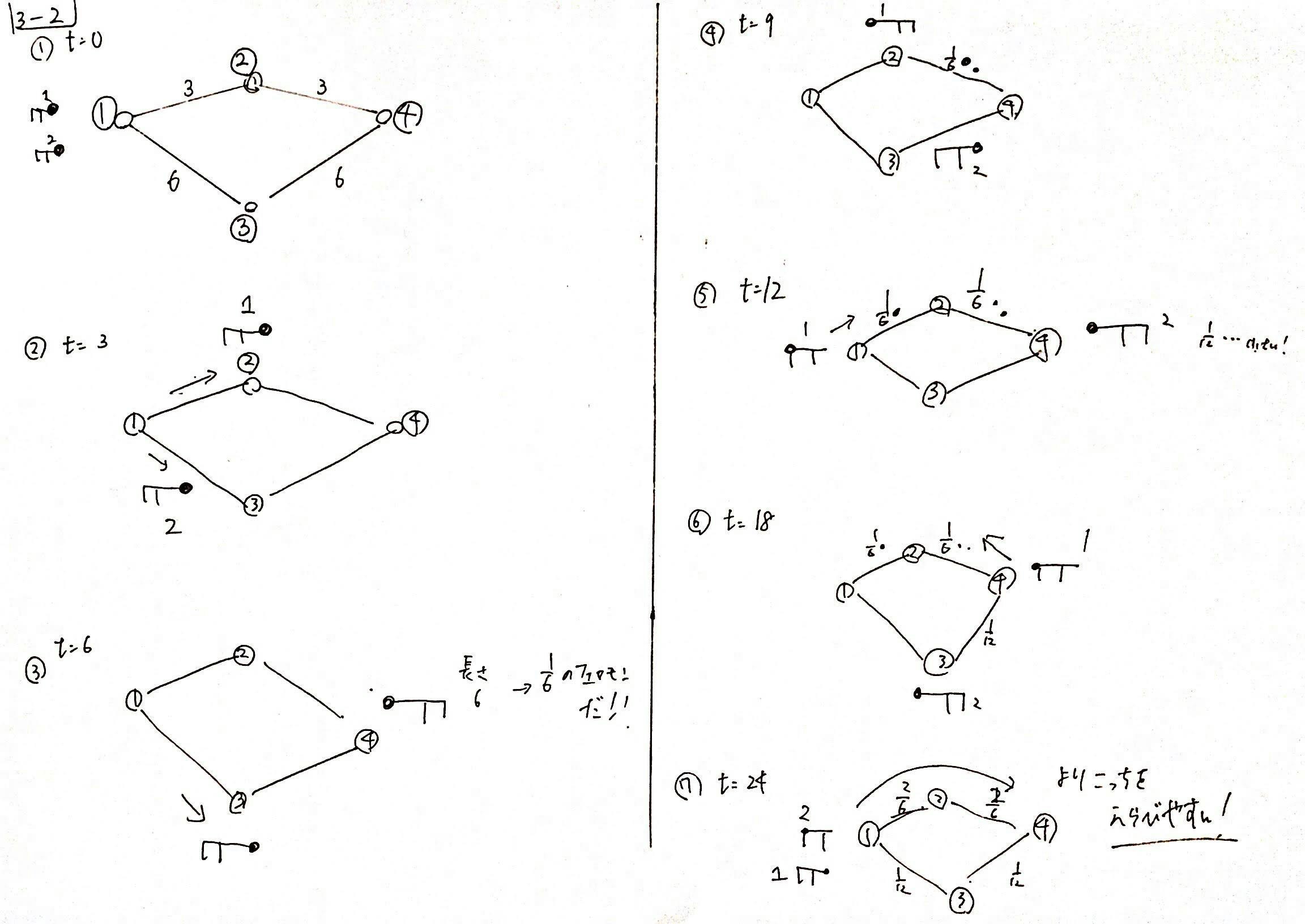
蟻(エージェント)が現在$2$匹、巣である頂点$1$にいるとします。
蟻たちは、巣$1$から移動を開始し、頂点$4$までの最短経路を発見しなくてはなりません。
まず、蟻たちは頂点$1$から移動を始めますが、フェロモンがどちらの辺にもありません。($e = (1, 2), (1, 3)$)
よって、蟻たちはそれぞれランダムに$1/2$の確率でどちらかの辺を選択します。
蟻は$2$匹いるため、頂点$2, 3$それぞれに$1$匹ずつ移動した場合を考えてみましょう。
蟻$1$は上の道を、蟻$2$は下の道を選んだようです。
$t=3$秒目では、早くも蟻$1$が頂点$2$にたどり着き、頂点$4$方向に進みました。
$t=6$秒目では、それぞれの蟻が頂点$4, 3$につき、蟻$1$のほうが目的地にすばやくたどり着きました。
このように、最短経路ほどより早く蟻はたどり着きます。
蟻$1$は以下のように考えました。
「僕が移動を開始して長さ$6$の移動で付いた。なので、$1/6$だけのフェロモンを帰りに分泌していこう。」
よって、蟻$1$は上記のフェロモン量を分泌しながらもと来た道を帰ります。
$t=9$秒目では、蟻$1$は早速フェロモンを分泌しています。
$t=12$秒目では、蟻$1$は巣に戻り、蟻$2$はようやく目的地に付きました。
蟻2は、長さ$12$もかかったので、帰り道には$1/12$しかフェロモンを分泌しないようです。
このように移動距離がながければ長いほど、分母が大きくなるため、帰り道のフェロモンが小さくなってしまいます。(フェロモンが大きいほどより選択されやすいので、移動距離が長いとフェロモンが小さい、つまり選択されづらくなります。うれしいですね。)
また、蟻$1$は、再び巣に向かいますが、辺$(1, 2), (1, 3)$を見ると、どうやら自分が分泌したフェロモンのある上の経路のほうがフェロモンがよく溜まっているようです。
そのため、上の経路をより大きい確率で選択氏、再び巣に向かいます。
(**ここで大事なのが、必ず上の経路を選択するわけではなく、小さい確率ですが下の経路も選択します。この確率による選択によって、局所解に陥ることを避けます。**この理由はこの節の最後に説明します。)
$t=18$では、蟻1は上の経路を選択するようです。これも同様に確率によって、より上の経路を選びやすいためです。
$t=24$では、蟻が両方もどり、上の経路のほうがより多くフェロモンが積まれています。
このように、蟻はフェロモン確率で道を選択し、これによって自然と最短経路に蟻が集まります。
これは、最短経路を通る蟻のほうがよりフェロモンを多くため、多くの蟻がそのフェロモンに釣られる、という正のフィードバックが起こるためです。
3-3. フェロモンの蒸発
上記のままでは、実はまだ完璧なACOのアイディアに至っていません。
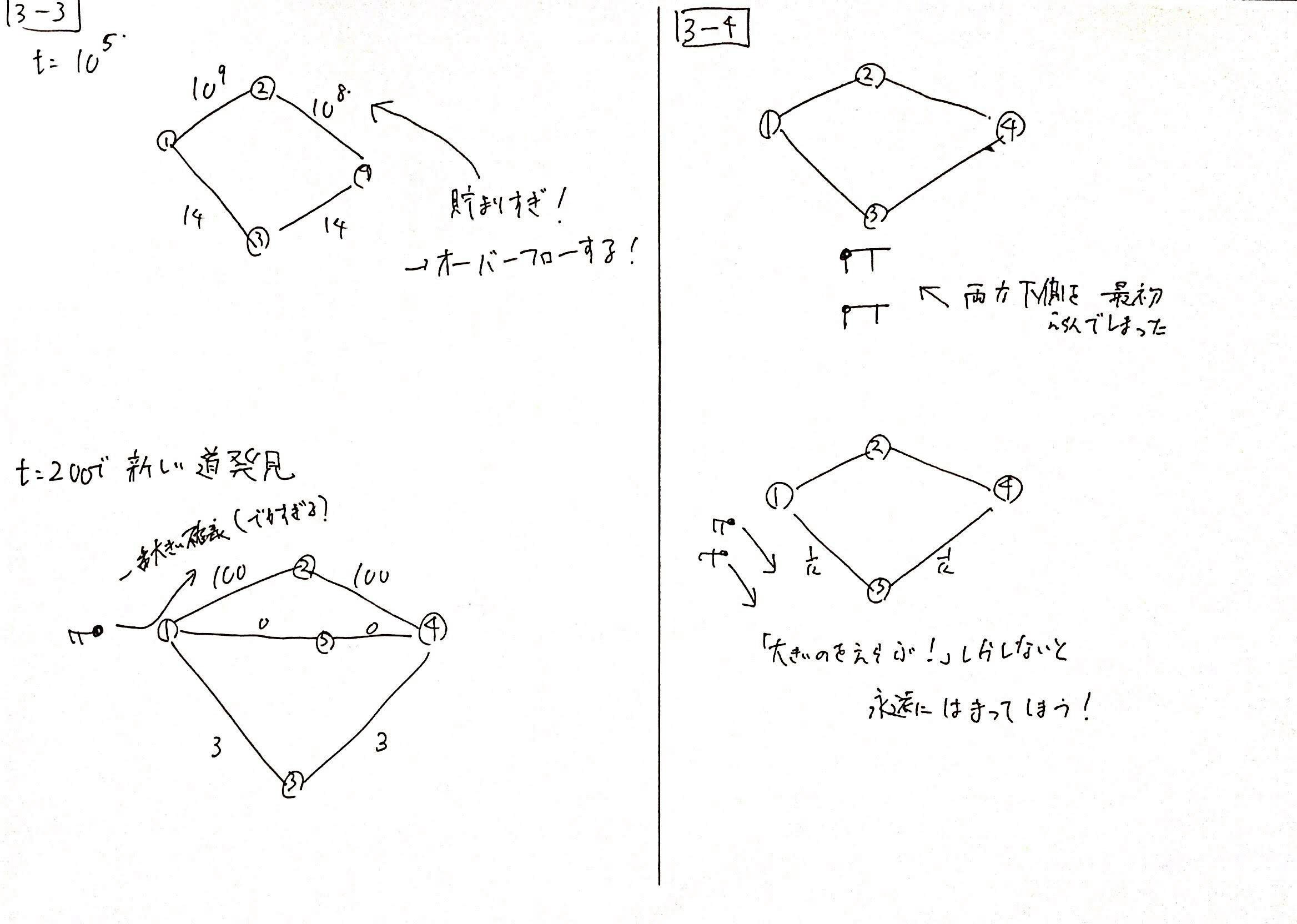
$t=10^5$秒目を考えてみます。
このとき、辺に溜まっているフェロモンが圧倒的な量になってしまう可能性があります。
実際のACOは蟻の数$N$が$N=100$などもっと多いため、このままではオーバーフローする可能性も避けられません。
また、もっとこのままでは駄目な理由として過去に溜まったフェロモンが永遠に残り続けて新しい可能性を閉ざしてしまうというものがあります。
$t=200$秒目で、実は中央に新しく道ができた、という状況を考えてみます。(例えば、溜まっていた水たまりが蒸発して道になったなど)
しかし、蟻は確率選択で道を選びますが、上の経路の値が大きすぎるため、中央の経路をなかなか選べません。結果として、本当はもっとよい経路があるのに、遠い経路のみを永遠にたどってしまいます。
そこで、フェロモンの蒸発という概念を取り入れます。
ACOでは、経過時間・サイクル$t$が$1$進むごとに、辺に溜まっているフェロモンが蒸発していきます。
具体的には、蒸発率${\rho}=0.9$などにします。
すると、例えば、$=200$で$100$のフェロモンが溜まっていても時間が経つにつれて
$200{\to}2000.9{\to}2000.9^2{\to}200*0.9^3$のようにどんどん$1$秒経過ごとに、フェロモンが蒸発し、現在の状態を重視になります。
この蒸発率は非常に大事なパラメータ・概念であり
${\rho}=0.1$のように小さすぎるとすぐにすべての辺のフェロモンが小さくなってしまって、完全なランダム選択と変わらなくなってしまいます。(フェロモンでせっかく最短経路を効率的に探せるのにこれでは無駄になってしまいます。)
また、${\rho}=0.9999$のように大きすぎると、フェロモンが一切蒸発せず、局所解に陥る可能性が非常に高いです。
3-4. 確率選択の嬉しさ
蟻はフェロモンの大きさによって、よりフェロモンの大きい道を、より大きい確率で選びますが、これの嬉しさは何でしょうか?
一番フェロモンの大きい経路を選ぶのは駄目なのでしょうか?
以下のような画像のように、最初の蟻たちがすべて下の経路を選んだ場合を考えてみます。
すると、永遠に下の経路を選び続けて、より良い上の経路を見つけることができません。
よって、確率選択をする嬉しさが分かると思います。
4. ACOの特徴
ACOのイメージを見てきました。
このように、ACOは、蟻たちが最短経路を発見する過程を、確率選択でシミュレーションする、というものに置き換えた最適化法になっています。
それでは、ACOの特徴とはどういうものがあるのでしょうか?
4-1. たくさんの蟻
ACOでは、多くの蟻を模したエージェントを、グラフネットワーク$G=(V, E)$上を移動させます。
これによって、もしどれかのエージェントが良くない経路を通ったとしても他のエージェントがより良い経路を通れば、群れ全体としては優良解を発見することができます。
このように、群れによって助け合うことで、大まかな最適解をミスなく求めることができます。
4-2. NP問題に強い
ACOが使用される問題は、ほとんどがNP困難と呼ばれる計算量が無限大にかかる、圧倒的に難しい問題です。
数理計画法などでは、小さいサイズでしか解けなかったり、そもそも解けないみたいな状況もあります。
しかし、ACOは必ず最適解を求められないし、毎回求まる答えが少し違う(確率選択なので)、というデメリットはありますが、
最適解に近い解を、小さい計算量で求めることができる!という特徴があります。
4-3. 変化のある問題に強い
ACOは、非常に変化のある問題に強いという特徴があります。
というのも、3で見てきたように、フェロモンの蒸発や確率選択という仕組みがあるため、シミュレーション中に急に問題設定(頂点数や辺の繋がり方)が変わっても、そのまま解き続けることができます。
しかし、数理計画法などの静的な計算方法は変化に弱いです。
そのため、ACOなどの群知能は変化に強いというメリットがあります。
(ただし、必ず変化を発見できるわけではありません。確率選択であり、局所解に陥って永遠に出れない可能性もあります。)
5. ACOモデル
ここまでだいぶ長くなってしまいました。
ついに、ACO・Ant Colony Optimizationの中身に入っていきます。
3, 4では最短経路について考えていましたが、ACOの実際のモデルは巡回セールスマン問題を考えていきます。
巡回セールスマン問題の詳細については、上記のWikipediaのリンクを参照ください。
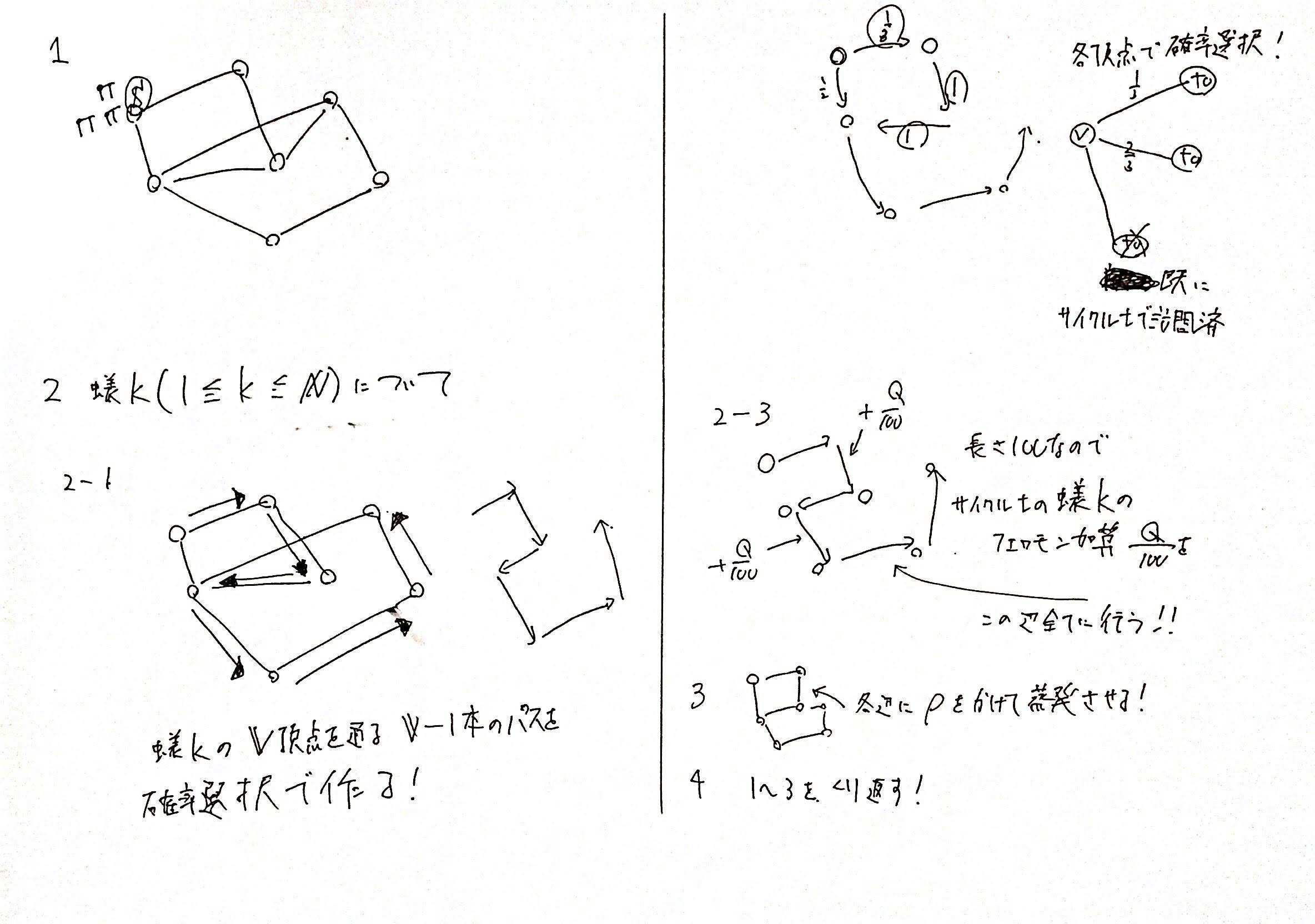
ACOで巡回セールスマン問題を解く際には、以下のような手順で行います。
- 蟻(エージェント)$N$体を、始点である$S$に配置する。
- サイクル$t$では、各蟻$k$ごとに以下の操作をする。
- 蟻$k$は、現在の頂点から移動できるかつまだ訪問していない頂点を結ぶ辺を、フェロモンによる確率で選択する。
- 2-1の処理を、$V$頂点すべて通るまで行う。(もしすべて通ることができない、つまり$V$頂点すべてをたどっていないのに、移動できる頂点がなくなったら、2-1をもう一度はじめから繰り返す。)
- サイクル$t$で、蟻$k$が通った$V-1$辺の長さの合計を計算する。(これを短くしたい)
- $Q / 長さの合計$を、蟻$k$が通ったパスに、サイクル$t$における蟻$k$の加算分としてフェロモンをグラフの辺に足す。
- 2の操作が$N$体分終わったら、フェロモンの蒸発を各辺ごとに行う。
- 規定サイクル数になるまで1~3を繰り返す。
という手順になります。
ここで大事なのが、蟻$k$、つまりエージェント$1$体ごとに$1$個の組み合わせ最適化問題の解を構築します。
つまり、この巡回セールスマン問題においては、蟻$k$ごとに、$V$頂点通るパスを確率選択で構築し、このパスが巡回セールスマンの解候補となります。
このように、蟻自体が通るパスが$1$個の解候補になるということに注意してください。(これらの解候補(巡回セールスマン問題だと通ったパスとその長さ)のうち、最も良いものを探す(最短距離)を見つけるのが目的です。)
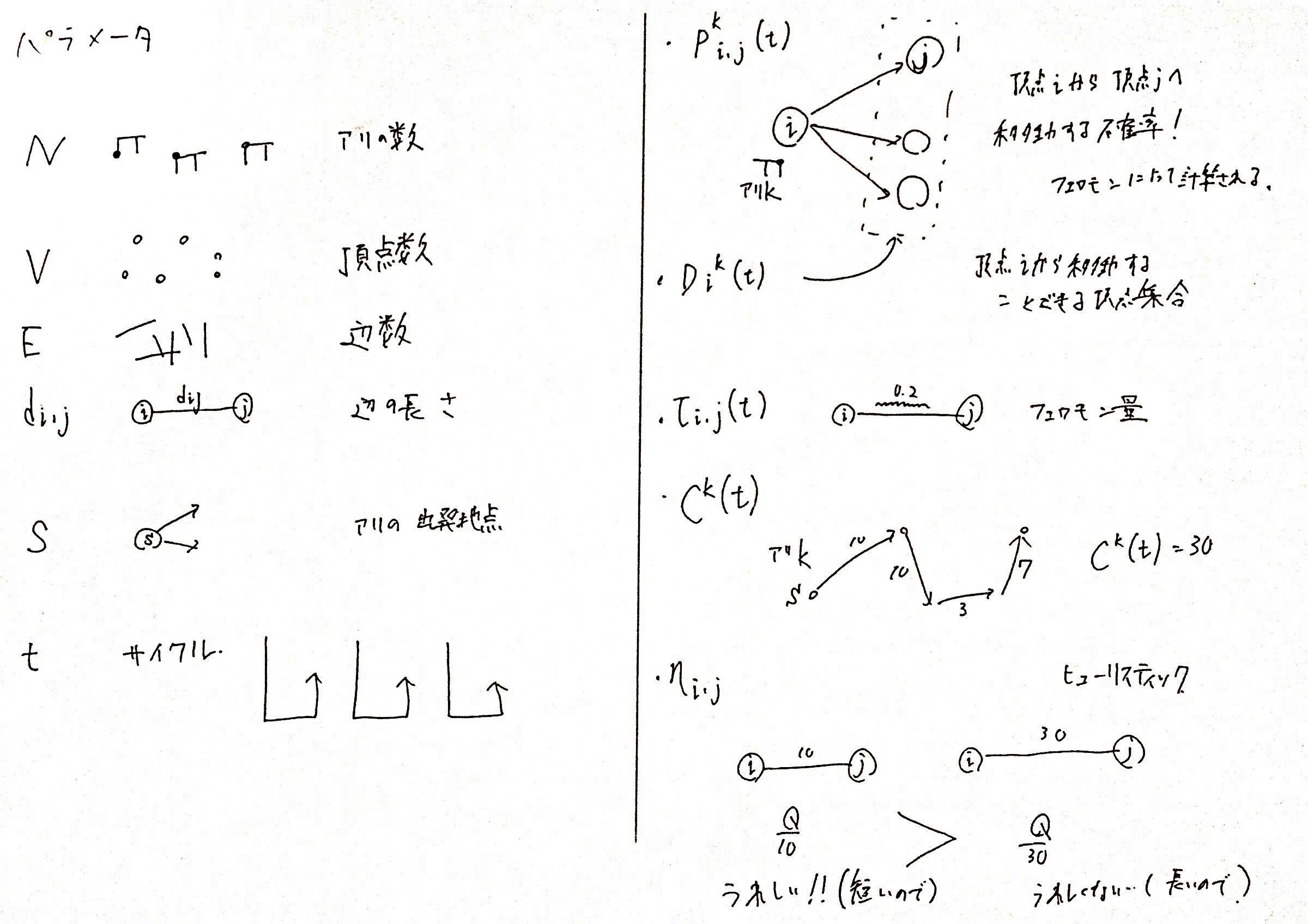
5-0. パラメータ
アントコロニー最適化では、非常に多くのパラメータが出てくるため以下にまとめます。
- $N$
- 蟻の数
- $V$
- グラフ$G=(V, E)$の頂点数
- $E$
- グラフ$G=(V, E)$の辺数
- $d_{i, j}$
- 頂点$i, j$を結ぶ辺$(i, j)$の長さ
- $S$
- 蟻が出発する頂点
- $t$
- サイクル$t$
- 「$N$体の蟻が始点$S$から移動して$N$個の巡回パスが構築され、その巡回パスの長さによってフェロモンを加算し、その後蒸発させる」までを$1$サイクルとして表す。
以上が直感的にわかりやすいもので共通して出てきます。
以下は、ACOの式に出てくるものであり、ACOの式を直接見たほうがわかりやすいかもしれません。
- $p_{i, j}^k(t)$
- サイクル$t$において、蟻$k$が頂点$i$にいるとき、頂点$j$を選ぶ確率
- フェロモンによって計算される
- $D_i^k(t)$
- サイクル$t$において、蟻$k$が頂点$i$にいるとき、頂点$i$から移動できる頂点集合
- すでに蟻$k$がサイクル$t$で訪問した頂点は含まれない
- ${\tau}_{i, j}(t)$
- サイクル$t$において、頂点$i, j$を結ぶ辺$(i, j)$に溜まっているフェロモン量
- $C^k(t)$
- サイクル$t$において、蟻$k$が構築した巡回パスの合計の長さ
- ${\eta}_{i, j}$
- 頂点$i, j$を結ぶ辺$(i, j)$のヒューリスティック値
- 辺$(i, j)$の嬉しさを表し、${\eta}_{i,j}$の値が大きいほど解が良くなるので、その辺を選びたいイメージ
- 巡回セールスマン問題では、${\eta}_{i,j} = {\frac{Q}{d_{i, j}}}$とすることが多い
- 上記だと辺の長さが短いほどヒューリスティック値が大きくなるため、より選びたくなる(移動経路を短くしたいので)
5-1. ACOの式
ACOの基本形では主に$3$つの式が出てきます。
5-1-1. 蟻kのパス選択確率式
ACOでは、$1$サイクルごとに、各蟻$k$がそれぞれ一個の巡回パスを構築します。
その際、蟻$k$が今いる頂点$i$から次のどの頂点に移動するかは、フェロモンによって決定されます。
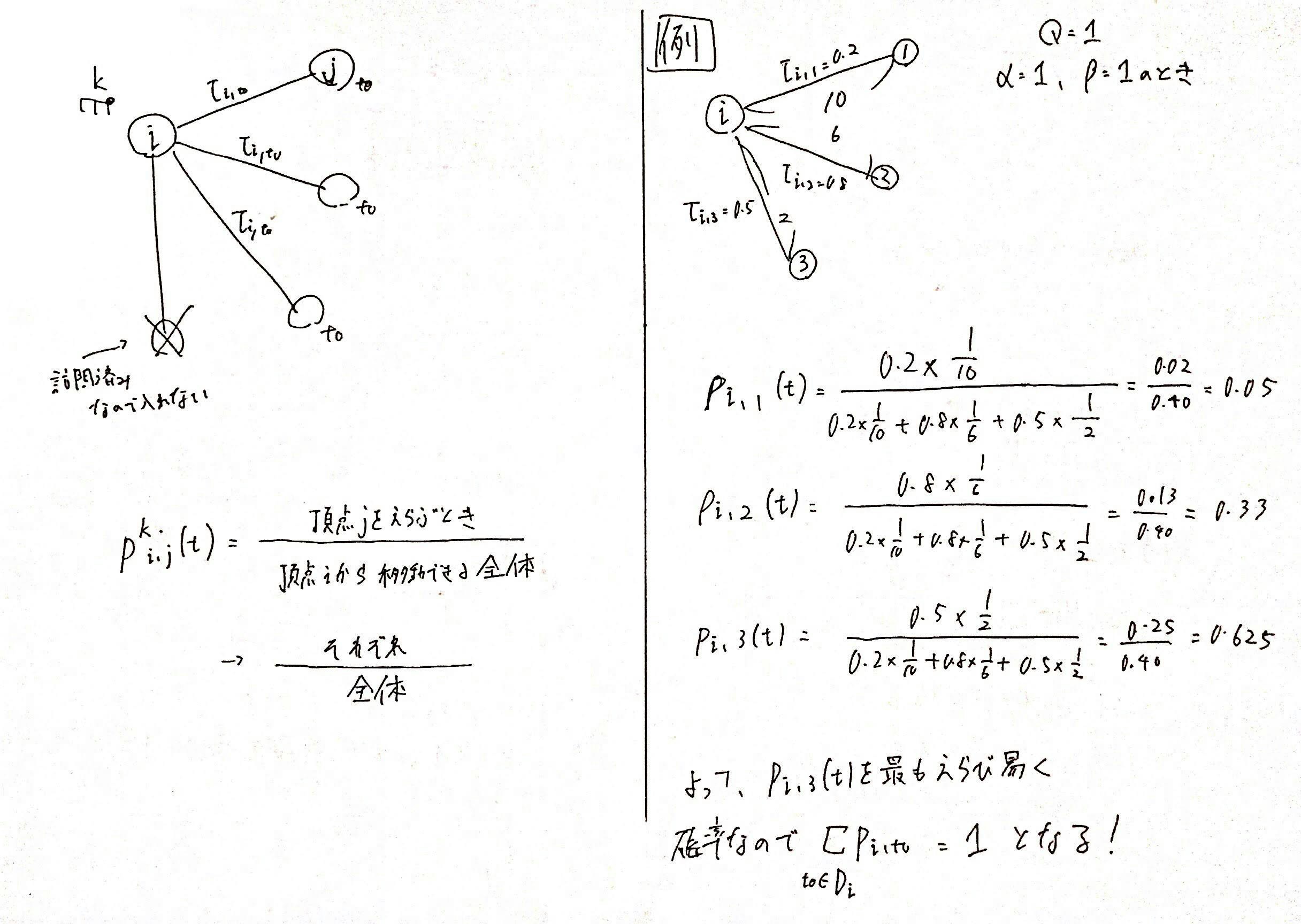
$$p_{i, j}^k(t) = {\frac{[{\tau}_{i, j}(t)]^{\alpha}[{\eta}_{i, j}]^{\beta}}{{\sum}_{to{\in}D_i} \ [{\tau}_{i, to}(t)]^{\alpha}[{\eta}_{i, to}]^{\beta}}}$$
$p_{i, j}^k(t)$は、サイクル$t$において、蟻$k$が頂点$i$にいるとき、そこから移動できる(まだ訪問していない)頂点$j$を選ぶ確率を表しています。
...よくわからないですね。
上の式は非常に複雑っぽく見えますがこれはただ
$$p_{i, j}^k(t) = {\frac{頂点jを選んだときの値}{(頂点jを選んだときの値)の合計(頂点iから移動できる分すべて)}}$$
となっています。
分子の$[{\tau}_{i, j}(t)]^{\alpha}[{\eta}_{i, j}]^{\beta}$は、フェロモンとヒューリスティックの値をかけ合わせたものになっています。
${\alpha}, {\beta}$はフェロモン、ヒューリスティックをどれくらい重視するかのパラメータで人間がプログラム上で設定しなければなりません。
フェロモンが大きいほど、分子の項は大きくなります。(フェロモンが大きいということは、より有望であると考えられるので)
また、ヒューリスティックが大きいほど(辺$(i, j)$が短いほど)、巡回パスが短くなる可能性が高いので、分子の項は大きくなります。
この${\alpha}, {\beta}$の設定によって、フェロモンを重視した探索をするか、もしくは辺の長さを重視して短い辺を強く選んでいくか?は、ユーザが決めなければなりません。
分母は、分子の値を頂点$i$から行ける分計算して足し合わせたものとなります。
よって、各蟻ごとに、各頂点で以上の計算を毎回行い、確率を求めて、どれかの辺を確率で選んで移動し、また上記の計算を行い確率を求めて、どれかの辺を確率で選んで移動し
を繰り返し、蟻$k$が一個の巡回パスを構築します。
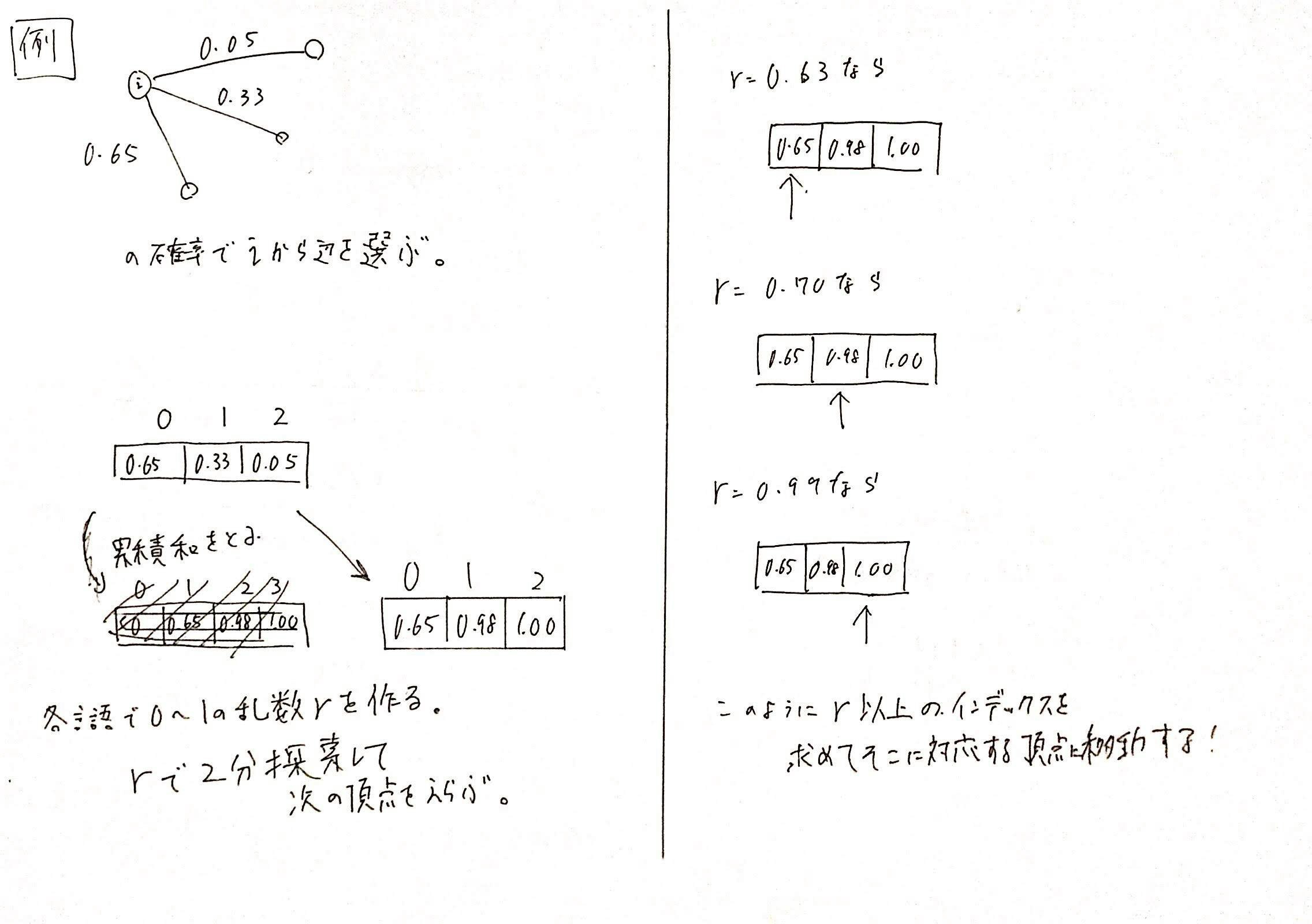
どう確率で辺を選ぶのか?
ここで、どう実際に確率で辺を選ぶのか?について考えましょう。
上の画像の例で考えます。(辺の長さが、図と一致していませんがご愛嬌です。)
頂点$i$から移動できる確率を配列に入れて、累積和と取ります。
(累積和が初めてのかたは検索するとおそらくでてきます。)
あとは、乱数$r = [0, 1)$を作って、二分探索をすればよいです。
こうすると、次に移動するべき頂点を選ぶことができます。
5-1-2. フェロモン計算式
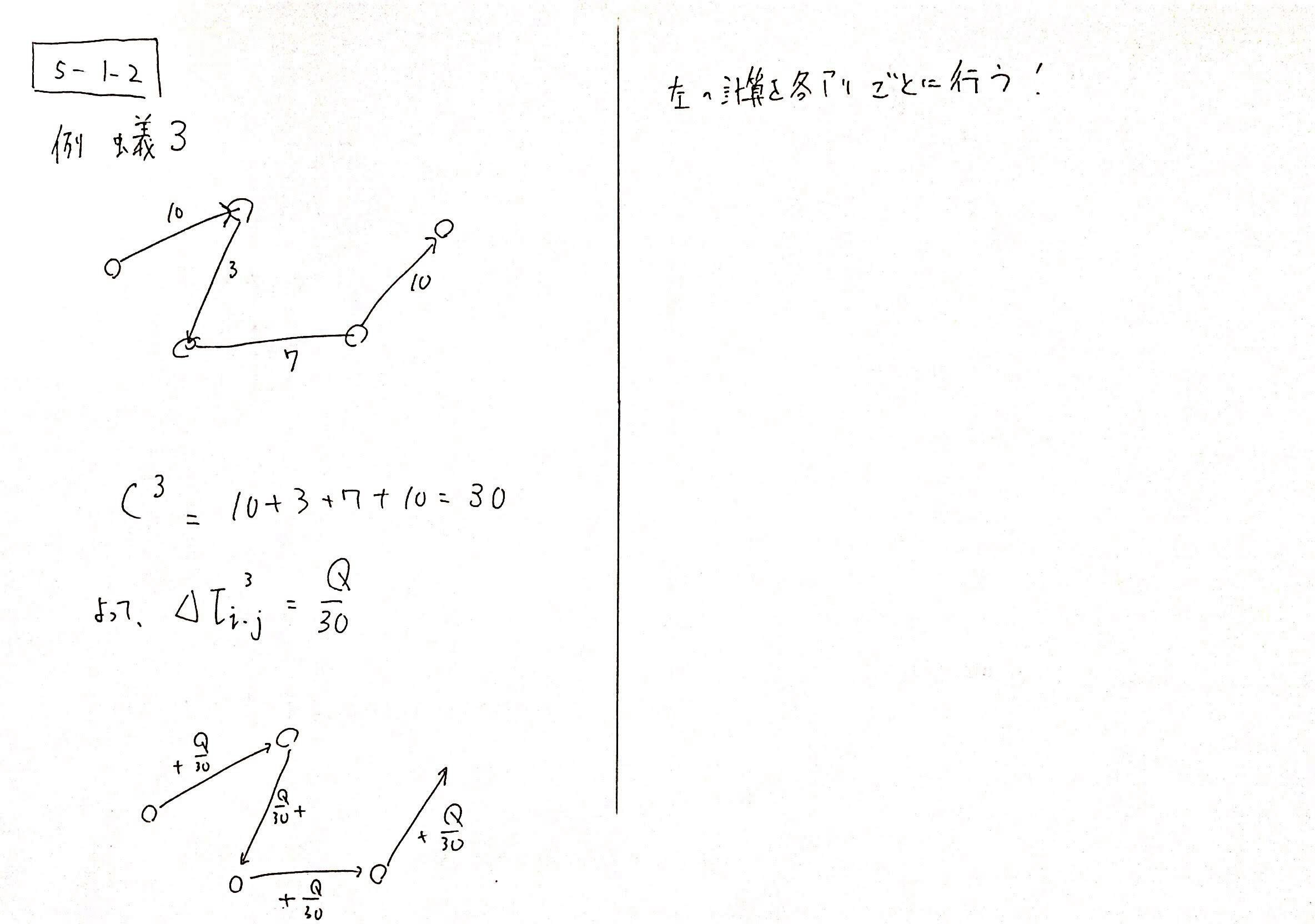
サイクル$t$で、蟻$N$体それぞれが巡回パスを構築したあとは、その巡回パスを元に、フェロモンをさらに加算します。(分泌するイメージです。)
蟻$i$が、通ってきた各辺に分泌するフェロモン量${\Delta}{\tau}_{i, j}^k$は以下のように計算されます。
$${\Delta}{\tau}_{i, j}^k = {\frac{Q}{C^k}} $$
ただし、${\Delta}{\tau}_{i, j}^k$は、蟻$k$がサイクル$t$で通ったパスにしかフェロモンが分泌されません。
例えば、$1{\to}2{\to}3{\to}4$のように移動したとき、$1{\to}2, 2{\to}3$などには蟻$k$によって分泌されますが、$1{\to}4$などの辺には分泌されません。
上記の式で、$C^k$は蟻$k$が通った巡回パスの長さの合計です。
そのため、巡回パスの長さが短ければ短いほどより多くのフェロモンが分泌されます。
$Q$はユーザが決めるパラメータです。
5-1-3. フェロモン更新式
最後にフェロモン更新式です。
この式は各サイクルの最後に行います。
つまり
- 各蟻が確立選択で巡回パスを構築する
- 各蟻の巡回パスの長さを計算して、加算するフェロモン量を計算する。
- 各道ごとにフェロモンを更新する(いまここ)
の、最後の部分になっています。
フェロモン更新式は以下のようになります。
$${\tau}_{i, j}(t+ 1) = {\rho}{\cdot}{\tau}_{i, j}(t) + {\sum}_{i=1}^N {\Delta}_{i, j}^k$$
このフェロモン更新式は各辺$(i, j)$ごとに実行するイメージです。
難しいので順番に見ていきます。
まず左辺の${\tau}_{i, j}(t+ 1)$は、次のサイクル$t+1$の各辺に貯まるフェロモンを表しています。
つまり、右側の値を計算して左辺に代入することで、次のサイクルを表します。
よって、あとは右辺の計算式を理解することになります。
まず、${\rho}{\cdot}{\tau}_{i, j}(t) $です。
${\tau}_{i, j}$は辺$(i, j)$に溜まっているフェロモン量を表しているのでした。
そして${\rho}$は蒸発率を表し、**どれぐらい今回のフェロモン量を加味するか?**を表します。
${\rho} = 0$なら、今回計算した新しい${\sum}_{i=1}^N {\Delta}_{i, j}^k$のみが次回のフェロモンになります。
${\rho} = 1$なら、今回計算した新しい${\sum}_{i=1}^N {\Delta}_{i, j}^k$に加えて、このサイクル$t$で残っていた${\tau}_{i, j}(t)$を完全に残すことになります。そのため、一切値は減らず永遠にフェロモンが増え続けます。
3-3で記述したとおり、可能な限り今回計算したフェロモンの値を加味しながら、これまでのフェロモン情報も利用したいです。
そのため、${\rho}=0.9$ぐらいにするのが通例なようです。
ついに${\sum}_{i=1}^N {\Delta}_{i, j}^k$の部分ですが、これは単純で辺$(i, j)$について、各蟻$k$が今回加算する分のフェロモンを合計しているだけです。
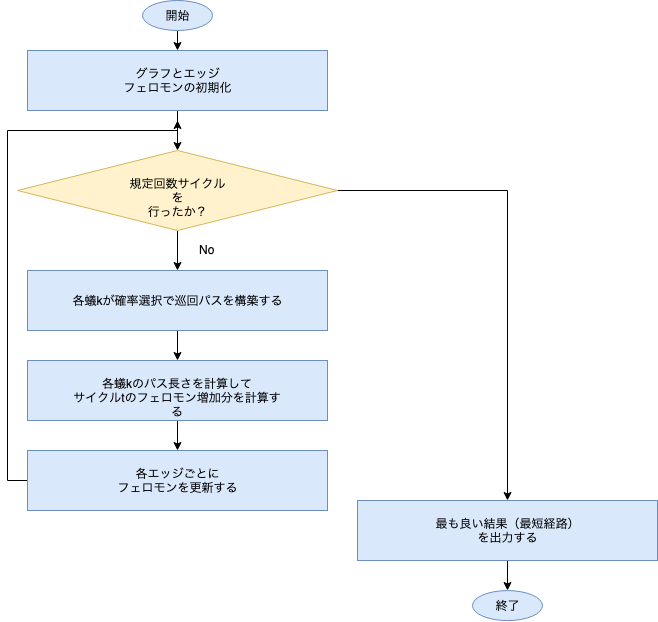
5-2. ACOのフローチャート
最後にフローチャートを見てみましょう。
実際は
「各エッジごとにフェロモンを更新する」
のあとに
「現時点で最もよい最短経路を構築した蟻$k$のパス・長さを保存する」
というものがありますが、省いています。(シンプルさのため)
6. ソースコード
それではPythonによる実装を見てみます。
ただ、あまり美しいものではないですが...(参照を使いまくっているため)
ソースコードのリポジトリはPyACOです。
pip install PyACO
でインストールして使用することができます。
6-0. 仕組み
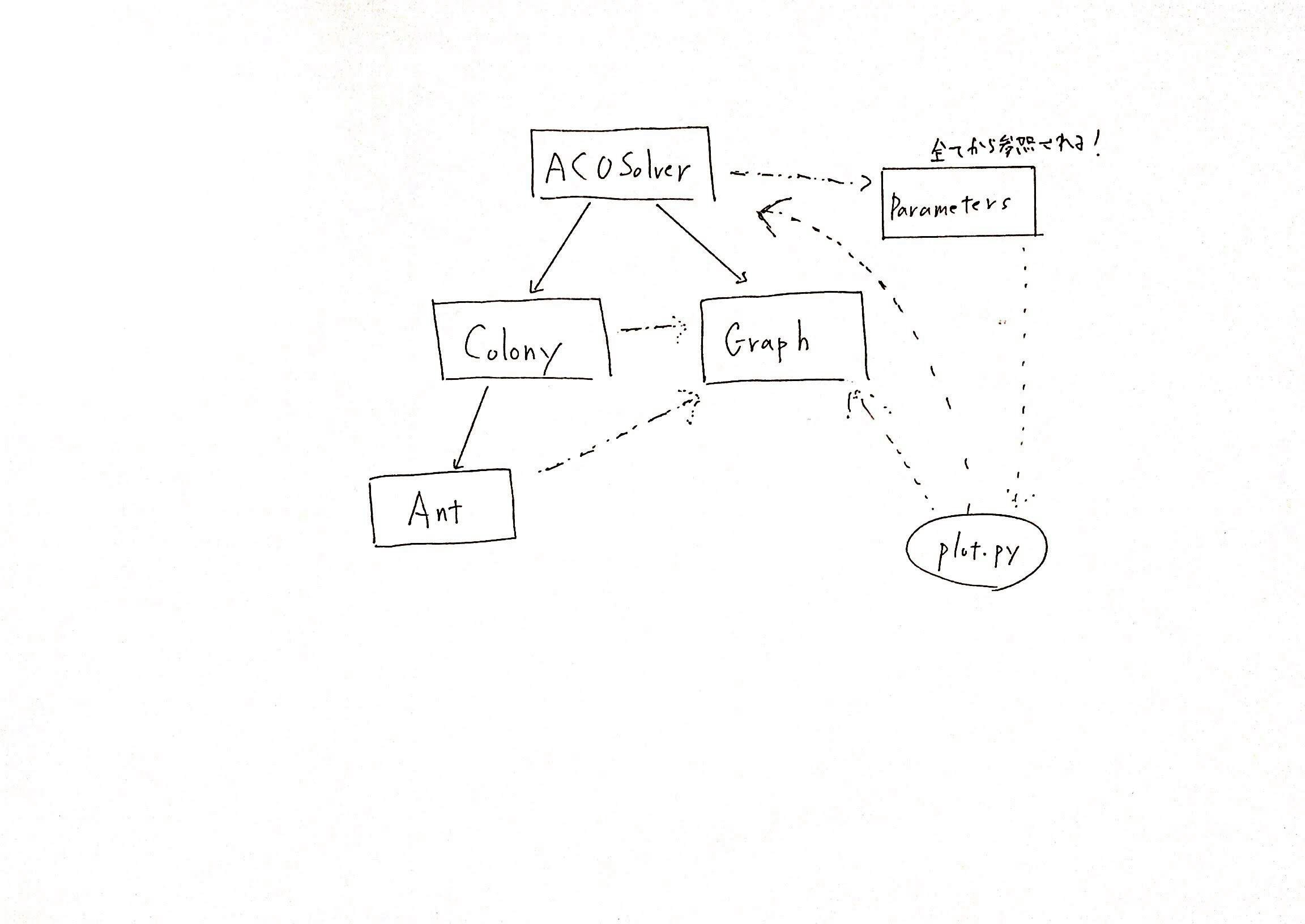
PyACOではいくつかのクラスに分割して作成されています。
- ACOSolver
- Parameters
- Colony
- Graph
- Ant
- plot
です。
ACOSolverは文字通り、main.pyから呼び出すソルバークラスで、ACO全体を管理します。
パラメータの初期化や、実際に実行するaco_runメソッドなどが記述されていたりします。
Parametersはあらゆるクラスから参照されるパラメータを保存するクラスです。
Pythonだと、クラスは必ず参照型になるので、ACOで使用するパラメータをすべて一個のクラスのメンバに保存して使用しています。
Colonyは、蟻Antを管理するクラスです。蟻を直接ACOSolverが管理すると複雑になるため、一個間に挟むために$N$体の蟻を一括管理するColonyクラスを用意しています。
Graphを参照しています。
Graphは、その名の通りグラフのクラスです。
各頂点の座標や各頂点間の距離、各頂点間のフェロモン量などを保存しています。
Antは、蟻のクラスです。Colonyから指示を出されて、実際にGraphクラスを参照してグラフ上を移動したり、構築したパスの長さを計算したりします。
plotはMatplitlibで、良いパスなどを描画するためのファイルです。
main.pyから
from PyACO.ACOSolver import ACOSolver
# Solverインスタンス
aco_solver = ACOSolver(num_of_ants=30, num_of_vertexes=50, Q=100, alpha=3, beta=5, rou=0.9, max_iterations=300,
initial_vertex=0, tau_min=0, tau_max=3000, ant_prob_random=0.1, super_not_change=30, plot_time=0.2)
# 実行
aco_solver.run_aco()
とすることで、ACOを実行できます。
6-1. ACOSolver
from PyACO.Parameters import Parameters
from PyACO.Colony import Colony
from PyACO.Graph import Graph
from PyACO import plot
class ACOSolver:
def __init__(self, num_of_ants, num_of_vertexes, Q, alpha, beta, rou, max_iterations, initial_vertex, tau_min,
tau_max, ant_prob_random, super_not_change, plot_time):
self.mC_parameters = Parameters(num_of_ants, num_of_vertexes, Q, alpha, beta, rou, max_iterations,
initial_vertex, tau_min,
tau_max, ant_prob_random, super_not_change, plot_time)
self.m_graph = Graph(self.mC_parameters)
self.m_colony = Colony(self.m_graph, self.mC_parameters)
self.m_best_ant = None
self.m_super_ant = None
self.m_cnt_super_not_change = 0
plot.init_plot()
def run_aco(self):
for T in range(self.mC_parameters.mC_max_iterations):
self.__update_aco()
self.__reset_aco()
if self.m_super_ant is None:
self.m_super_ant = self.m_best_ant
if self.m_super_ant[0] > self.m_best_ant[0]:
self.m_super_ant = self.m_best_ant
else:
self.m_cnt_super_not_change += 1
# 答えが局所解に陥ったら強制的にフェロモンを初期化する
if self.m_cnt_super_not_change > self.mC_parameters.mC_super_not_change:
self.reset_pheromones()
self.m_cnt_super_not_change = 0
print(T, self.m_super_ant)
plot.play_plot(self.m_graph.m_coordinates, self.m_super_ant[1], self.m_best_ant[1],
self.mC_parameters.mC_plot_time)
def reset_pheromones(self):
self.m_graph.reset_graph_when_stagnation()
def __update_aco(self):
self.m_colony.update_colony()
self.__update_next_pheromones()
self.m_best_ant = self.m_colony.get_best_ant_path()
def __reset_aco(self):
self.m_colony.reset_colony()
self.m_graph.reset_graph()
def __update_next_pheromones(self):
num_of_vertexes = self.mC_parameters.mC_num_of_vertexes
rou = self.mC_parameters.mC_rou
tau_min = self.mC_parameters.mC_tau_min
tau_max = self.mC_parameters.mC_tau_max
for i in range(num_of_vertexes):
for j in range(num_of_vertexes):
self.m_graph.m_edge_pheromone[i][j] = self.m_graph.m_edge_pheromone[i][j] * rou + \
self.m_graph.m_edge_next_pheromone[i][j]
for i in range(num_of_vertexes):
for j in range(num_of_vertexes):
self.m_graph.m_edge_pheromone[i][j] = min(tau_max, max(self.m_graph.m_edge_pheromone[i][j], tau_min))
ACOSolverクラスです。
init
initでは、初期化を行っています。
パラメータやグラフ、コロニーの初期化を行い、参照を保存しています。
run_aco
run_acoを外部からされると、mC_max_iterations回ACOのサイクルの実行を行います。
mCは、メンバ変数かつ**変更しないで〜**という意味のconstのCをつけています。PythonにConstが無いのが怖いです。
m_super_antはこれまでの$0$~$T$サイクルで最も良い結果を出した蟻の情報を保存しています。
m_best_antは今回の$T$サイクルで最も良い結果を出した蟻の情報を保存しています。
reset_pheromones
フェロモンをリセットします。
フェロモンはGraphクラスにあるので、Graphにフェロモンをリセットするよう指示を出しています。
__update_aco
メソッドに__が付いている場合、このクラス内でしか使用されないprivateメソッドです。
外部から呼び出されません。
updateという名前が紛らわしいですが、サイクル$t$における一連処理の実行を表しています。
コロニーに処理を依頼し、フェロモンを更新して、最も良い蟻の情報を取得します。
__update_next_pheromones
フェロモンを更新します。
サイクル$t+1$用に更新しています。
基本的にはフェロモン更新式と同じですが${\tau}_{min}, {\tau}_{max}$というものが出てきています。
これは、フェロモンの下限と上限を決めることで、局所解に陥ることを避ける効果があります。
MIN MAX Antと呼ばれます。
6-2. Parameters
class Parameters:
def __init__(self, num_of_ants, num_of_vertexes, Q, alpha, beta, rou, max_iterations, initial_vertex, tau_min,
tau_max, ant_prob_random, super_not_change, plot_time):
self.mC_num_of_ants = num_of_ants
self.mC_num_of_vertexes = num_of_vertexes
self.mC_Q = Q
self.mC_alpha = alpha
self.mC_beta = beta
self.mC_rou = rou
self.mC_max_iterations = max_iterations
self.mC_initial_vertex = initial_vertex
self.mC_tau_min = tau_min
self.mC_tau_max = tau_max
self.mC_ant_prob_random = ant_prob_random
self.mC_super_not_change = super_not_change
self.mC_plot_time = plot_time
パラメータを集めるクラスです。
6-3. Colony
from PyACO.Ant import Ant
from copy import deepcopy
class Colony:
def __init__(self, graph, parameters):
self.m_num_of_ants = parameters.mC_num_of_ants
self.m_parameters = parameters
self.m_graph = graph
self.m_ants = [Ant(self.m_graph, self.m_parameters) for i in range(self.m_num_of_ants)]
def update_colony(self):
self.__construct_ants()
self.__calc_next_pheromones()
def get_best_ant_path(self):
length = 1e20
path = []
for ant in self.m_ants:
if ant.calc_all_path_length() < length:
length = ant.calc_all_path_length()
path = deepcopy(ant.m_visited_path)
return [length, path]
def reset_colony(self):
for ant in self.m_ants:
ant.reset_ant()
def __construct_ants(self):
for ant in self.m_ants:
ant.construct_path()
def __calc_next_pheromones(self):
for ant in self.m_ants:
ant.calc_next_pheromone()
ACOSolverクラスから指示をもらって、Antをまとめて管理するクラスです。
init
初期化をします。
グラフなどの参照を保存します。
update_colony
ACOSolverから、サイクルを実行するように呼び出されます。
蟻たちに実際にパスを構築させて、フェロモンの分泌量を計算します。
get_best_ant_path
蟻たちのうち、もっとも良いパスを取得します。
reset_colony
蟻たちを毎回のサイクルごとに初期化する必要があるため、そのための関数です。
__constructs_ants
蟻たちにパスを構築するよう指示を出します。
__calc_next_pheromons
フェロモンをありたちに計算してもらいます。
つまり、構築したパスの長さを計算して、$Q$を割っています。
6-4. Graph
Graphクラスです。
import random
import math
class Graph:
def __init__(self, parameters):
self.m_num_of_vertexes = parameters.mC_num_of_vertexes
self.m_coordinates = [None] * self.m_num_of_vertexes
self.m_edge_length = [[0 for j in range(self.m_num_of_vertexes)] for i in range(self.m_num_of_vertexes)]
self.m_edge_pheromone = [[0 for j in range(self.m_num_of_vertexes)] for i in range(self.m_num_of_vertexes)]
self.m_edge_heuristics = [[0 for j in range(self.m_num_of_vertexes)] for i in range(self.m_num_of_vertexes)]
self.m_edge_next_pheromone = [[0 for j in range(self.m_num_of_vertexes)] for i in
range(self.m_num_of_vertexes)]
self.m_parameters = parameters
self.__prepare_graph()
def __prepare_graph(self):
for i in range(self.m_num_of_vertexes):
self.m_coordinates[i] = (random.uniform(0, 1000), random.uniform(0, 1000))
for i in range(self.m_num_of_vertexes):
for j in range(self.m_num_of_vertexes):
self.m_edge_length[i][j] = Graph.__calc_edge_length(self.m_coordinates[i], self.m_coordinates[j])
for i in range(self.m_num_of_vertexes):
for j in range(self.m_num_of_vertexes):
if i < j:
self.m_edge_pheromone[i][j] = self.m_parameters.mC_Q / self.m_edge_length[i][j]
self.m_edge_pheromone[j][i] = self.m_parameters.mC_Q / self.m_edge_length[i][j]
for i in range(self.m_num_of_vertexes):
for j in range(self.m_num_of_vertexes):
if i < j:
h = self.m_parameters.mC_Q / self.m_edge_length[i][j]
self.m_edge_heuristics[i][j] = h
self.m_edge_heuristics[j][i] = h
def reset_graph(self):
self.m_edge_next_pheromone = [[0 for j in range(self.m_num_of_vertexes)] for i in
range(self.m_num_of_vertexes)]
def reset_graph_when_stagnation(self):
for i in range(self.m_num_of_vertexes):
for j in range(self.m_num_of_vertexes):
if i < j:
self.m_edge_pheromone[i][j] = self.m_parameters.mC_Q / self.m_edge_length[i][j]
self.m_edge_pheromone[j][i] = self.m_parameters.mC_Q / self.m_edge_length[i][j]
@staticmethod
def __calc_edge_length(p1, p2):
dx = (p1[0] - p2[0]) ** 2
dy = (p1[1] - p2[1]) ** 2
return math.sqrt(dx + dy)
ほとんどのクラスから参照されます。
__prepare_graph
グラフの情報を初期化します。一回だけinitから呼ばれるのみです。
m_coordinatesは各頂点の座標です。
m_edge_lengthは各頂点間の距離です。
m_edge_pheromoneは各頂点間のフェロモン量です。最初は$Q / edge_{i,j}$で初期化しています。
m_edge_heuristicsは各頂点間の辺のヒューリスティック値です。$h_{i,j}$と式だと表されていました。
reset_graph
グラフ情報をリセットします。
ただし、m_edge_pheromoneなどはフェロモン情報なので消しません。
リセットするのは、m_edge_next_pheromoneの次のフェロモン量を計算するための一時配列のみです。
reset_graph_when_stagnation
蟻たちが構築したパスに変化が訪れなくなり局所解に陥ったときに強制的にフェロモンを初期化します。
ACOSolverから呼ばれます。
6-5. Ant
import random
import bisect
class Ant:
def __init__(self, graph, parameters):
self.m_graph = graph
self.m_visited_vertex = [False for i in range(parameters.mC_num_of_vertexes)]
self.m_visited_path = []
self.m_num_of_vertex = parameters.mC_num_of_vertexes
self.m_parameters = parameters
self.m_init_vertex = parameters.mC_initial_vertex
def construct_path(self):
self.m_visited_path.append(self.m_init_vertex)
self.m_visited_vertex[self.m_init_vertex] = True
for i in range(self.m_num_of_vertex - 1):
# 現在の頂点
v = self.m_visited_path[-1]
# 頂点vから移動できる頂点と確率を求める
to_vertexes, to_prob = self.__calc_prob_from_v(v)
to = -1
# もし一様乱数よりも小さいなら、完全ランダムで選ぶ
if random.random() < self.m_parameters.mC_ant_prob_random:
to = to_vertexes[random.randint(0, len(to_vertexes) - 1)]
else:
# 確率選択を行う
random_p = random.uniform(0.0, 0.999999999)
to = to_vertexes[bisect.bisect_left(to_prob, random_p)]
# toは次に向かう頂点で、pathに追加する
self.m_visited_path.append(to)
self.m_visited_vertex[to] = True
def calc_next_pheromone(self):
length = self.calc_all_path_length()
Q = self.m_parameters.mC_Q
for i in range(self.m_num_of_vertex - 1):
self.m_graph.m_edge_next_pheromone[self.m_visited_path[i]][self.m_visited_path[i + 1]] += Q / length
def calc_all_path_length(self):
length = 0
for i in range(self.m_num_of_vertex - 1):
length += self.m_graph.m_edge_length[self.m_visited_path[i]][self.m_visited_path[i + 1]]
return length
def __calc_prob_from_v(self, v):
# 確率の合計(分母)
sumV = 0
# 行き先候補情報
to_vertexes = []
to_pheromones = []
alpha = self.m_parameters.mC_alpha
beta = self.m_parameters.mC_beta
for to in range(self.m_num_of_vertex):
# すでに訪ねていたら
if (to == v) or self.m_visited_vertex[to]:
continue
# フェロモン分子の計算
pheromone = self.m_graph.m_edge_pheromone[v][to] ** alpha * self.m_graph.m_edge_heuristics[v][to] ** beta
sumV += pheromone
# 候補に足す
to_vertexes.append(to)
to_pheromones.append(pheromone)
# 分母で割る
to_prob = [x / sumV for x in to_pheromones]
# 確率の累積和を取る
for i in range(len(to_prob) - 1):
to_prob[i + 1] += to_prob[i]
# 行き先の頂点集合と確率を返す
return to_vertexes, to_prob
def reset_ant(self):
self.m_visited_vertex = [False for i in range(self.m_parameters.mC_num_of_vertexes)]
self.m_visited_path = []
蟻のクラスです。
init
m_visited_vertexは、$N$個の頂点のうち、このサイクル$t$においてどの頂点を訪ねたか?をTrue, Falseで管理します。
一方、m_visited_pathは実際に通った順番で頂点を配列に追加していきます。
construct_path
実際にパスを構築します。
現段階のコードでは、$V{\times}V$の各頂点間にエッジがある場合しか想定していません。
折をみて、エッジがたまにない場合のコードに更新します。
# もし一様乱数よりも小さいなら、完全ランダムで選ぶ
if random.random() < self.m_parameters.mC_ant_prob_random:
to = to_vertexes[random.randint(0, len(to_vertexes) - 1)]
上記のコードですが、これはmC_ant_prob_randomよりも一様乱数が小さいなら、これまで説明した確率によるパス選択をやめて、完全にランダムに次の頂点を選択します。
つまり、$5$頂点次の候補があれば、${\frac{1}{5}}$の確率で選択します。
このコードを書くことによって、完全なランダム選択も行うことで、局所解に陥り辛くなります。
ただ、この完全なランダム選択の割合を増やしすぎると、フェロモン関係なくランダムに移動するだけになってしまうため注意です。
__calc_prob_from_v
頂点$v$から次に移動できる頂点への各移動確率を計算します。
頂点$v$から行ける頂点集合$to$について、分子の値を計算しながら分母、つまり合計を計算し、最後に割っています。
calc_all_path_length
蟻$k$のパスの長さを計算します。
Graphを参照して計算します。
calc_next_pheromone
蟻$k$について、通ったパスのフェロモンの分泌量を計算します。
Graphのm_edge_next_pheromoneは今回分泌するフェロモンを貯める一時配列で
あとで、ACOSolverの__update_next_pheromonesで、m_edge_pheromonesに加算されます。
6-6. plot
plotクラスです。
import matplotlib.pyplot as plt
def init_plot():
plt.ion()
plt.title("ACO")
plt.xlim(0, 1000)
plt.ylim(0, 1000)
plt.xlabel("x")
plt.ylabel("y")
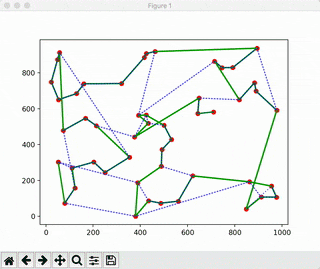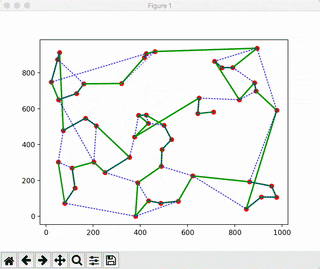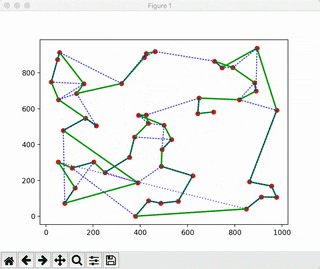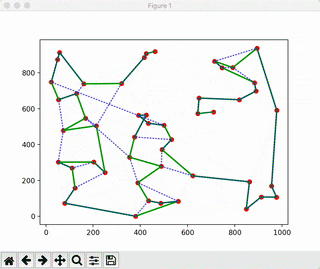
def play_plot(coordinates, super_path, best_path, plot_time):
X = [xy[0] for xy in coordinates]
Y = [xy[1] for xy in coordinates]
plt.plot(X, Y, "o", c="red")
super_x = [[coordinates[super_path[i]][0], coordinates[super_path[i + 1]][0]] for i in range(len(coordinates) - 1)]
super_y = [[coordinates[super_path[i]][1], coordinates[super_path[i + 1]][1]] for i in range(len(coordinates) - 1)]
best_x = [[coordinates[best_path[i]][0], coordinates[best_path[i + 1]][0]] for i in range(len(coordinates) - 1)]
best_y = [[coordinates[best_path[i]][1], coordinates[best_path[i + 1]][1]] for i in range(len(coordinates) - 1)]
plt.plot(super_x, super_y, c="green", linewidth=2)
plt.plot(best_x, best_y, c="blue", ls=":", alpha=0.7)
plt.draw()
plt.pause(plot_time)
plt.cla()
plotをします。
7. ソースコードの配布
pip install ACO
でインストールできます。
バージョンアップを予定しています。
8. ACOの拡張
色々とACOの内容を見てきました。
しかし、これは最もシンプルなACOです。
そのほかにどのようなACOの発展版があるのでしょうか?
8-1. Max-Min ACO
ソースコードにも出てきましたが、フェロモンの更新時に
下限と上限を定めます。
これによって、フェロモンが少なすぎて選択されない、もしくはフェロモンが多すぎて選択されすぎる道の出現を避けることで、局所解に陥ることを避けることができます。
ここでいう局所解に陥るというのは、同じパスばかり選択肢してさらにより良い解を発見できないという意味です。
8-2. ASbest
普通のACOでは、フェロモンの更新時に普通は$N$体の蟻全部についてフェロモンの分泌計算を行い、フェロモンを更新します。
一方、ASbestは、サイクル$t$において、最もよい結果を残した蟻のみがフェロモンの更新を行います。
(ちなみにASとはAnt-SystemでMarco Dorigo氏が開発した最初のACOをAnt-Systemと呼びます。)
これによって、より良い蟻がフェロモンをさらに強化し、素早く処理を行うことができます(局所解におそらく陥りやすいです)
8-3. ASrank
ASbestの弱点を補ったACOです。
ASbestでは最も良い結果のみを残した蟻でフェロモン分泌を行いますが、ASrankでは蟻をそれぞれソートして重み付けをしてフェロモン分泌を行います。
これによって、ASbestよりも局所解を避けながら、効率良く探索を行えます。
9. ACOの応用例
ACOは、TSPでよくベンチマークテストが取られますが、現実の応用問題にも適用することができます。
9-1. 輸送問題
ヤマト運輸などのトラック運営会社では、効率良く運送パスを求めることが求められます。
適当に運送していたらいくら経っても運送が終了しません。
そこで、ACOを利用して、運送パスを求めることが可能です。(可能らしいです、まだ論文を理解できてないので...)
ACOの特徴であるロバスト性や、変化に強いという点から、トラックの運転手さんが急に再配達を頼まれた際の新しい経路構築などで有効であると考えられます。
9-2. ネットワークパケット問題
ネットワークでは、日に日に通信されるデータ量が増加しています。
そこで、ACOをネットワークのパケットの輸送パス計算に利用することで、特定のリンクに通信が集中することを避けることが可能となります。
また、現在非常にIoTの発展によって注目されている、メッシュネットワーク・ワイヤレスセンサネットワークなどでACOを利用しようとする研究が増えています。
9-3. 集合被覆問題
集合をどうカバーするか?に使えるようです。
論文はやくよまないといけないです...
9-4. 最小全域木
最小全域木をどうやらACOで求めることができるようです。
ちょっとどうやっているか想像つかないので、論文早く読まないといけません。
おそらく、ACOで求めるメリットは動的にグラフの状態が変わる場合に最小全域木を求めたい!というときに有効なのだと思います。
まとめ
ACOについて見てきました。
ACOを含む群知能は、人工知能やDeepLearningなどと比べるとそこまで名前が知られている技術ではありません。
しかし、人間は生物から多く学ぶべきことがあり、人間にはできないことを彼らは群れとして実現しています。
これからの研究では、AIやDeepLearningに、群知能が複合されて、さらに強い効果を出すのではないかと考えています。