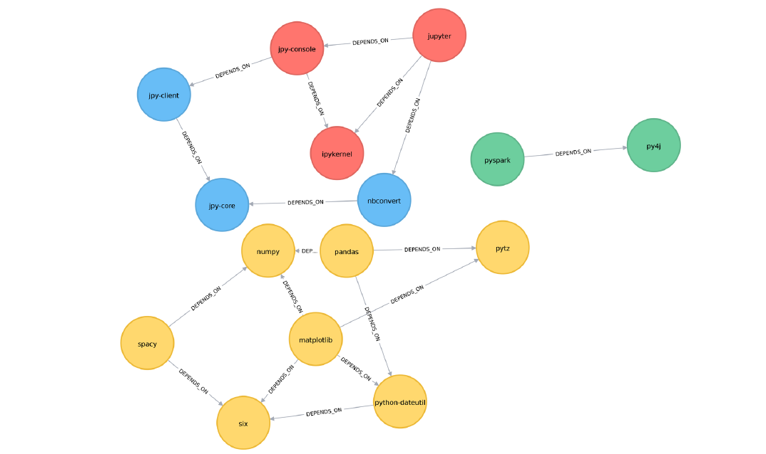
はじめに
UL Systems Advent Calendar 2019 - 10日目。
本日は、グラフアルゴリズムについてご紹介したいと思います。
NoSQLの1つのカテゴリーとして存在感を増しているグラフデータベースですが、純粋なデータベースとしての機能(データの保存、データの取出し)以外にもビジュアライゼーション機能やグラフアルゴリズム機能が組み込みで提供されるケースが増えてきました。グラフデータベースとして人気の高い1 Neo4j も分析用のグラフアルゴリズムをデフォルトで組み込み、今やデータベースというより、データプラットフォームとして進化を続けています。
といわけで、本日はグラフアルゴリズムについてお話していきたいと思います。
その前に、グラフデータベースとは? を知りたい方は、本日紹介する Neo4j と Oracle PGX の説明スライドをご参照下さい。
[ 異次元のグラフデータベースNeo4j ]
https://www.slideshare.net/ssuser78387c/neo4j-119992868
[ Oracle Labs 発! Parallel Graph AnalytiX(PGX)]
https://www.slideshare.net/oracle4engineer/oracle-labs-pgx
グラフアルゴリズムのカテゴリー
まずは、グラフアルゴリズムについて代表的なカテゴリーをざっくりと紹介します。
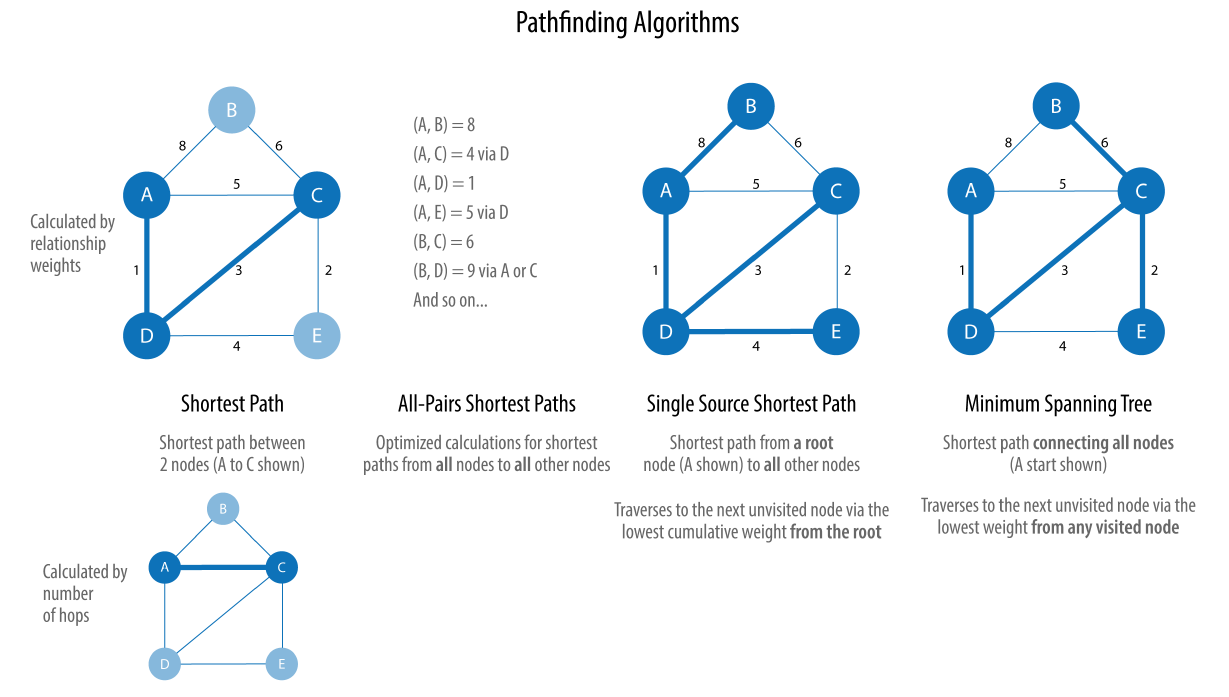
経路探索
ノード間に存在する様々な経路を求めるアルゴリズムです。
あるノードからあるノードへの到達可能性や、最短経路の探索など経路に関するアルゴリズムは、日常生活の中でもお馴染みであり比較的にポピュラーなカテゴリーと言えます。
最短経路は距離に関心を寄せているわけですが、例えば 問題設定を時間や金額に読み替えると、最速経路や最安経路に様変わりできます。また2点間だけでなくグラフ上の全ノードを繋ぐ経路を求めたり、色々な経路探索の仕方があります。
書籍: O'reilly Graph Algorithms: Practical Examples in Apache Spark and Neo4j より
コミュニティ検出
グラフ構造をもとに各ノードがどのようなコミュニティに属しているのか(形成しているのか)を検出するアルゴリズムです。
統計的機械学習の教師無し学習のクラスタリングと似ています。統計的機械学習のクラスタリングでは、データの属性値をヒントにクラスターを見つけていきますが、グラフアルゴリズム流のコミュニティ検知は関係性をヒントにしてコミュニティを見つけていきます。ノード間の関係はエッジで与えられているので、各ノード間の関係性をもとに どのノードとどのノードが同じコミュニティに属しているかを推察していきます。
書籍: O'reilly Graph Algorithms: Practical Examples in Apache Spark and Neo4j より
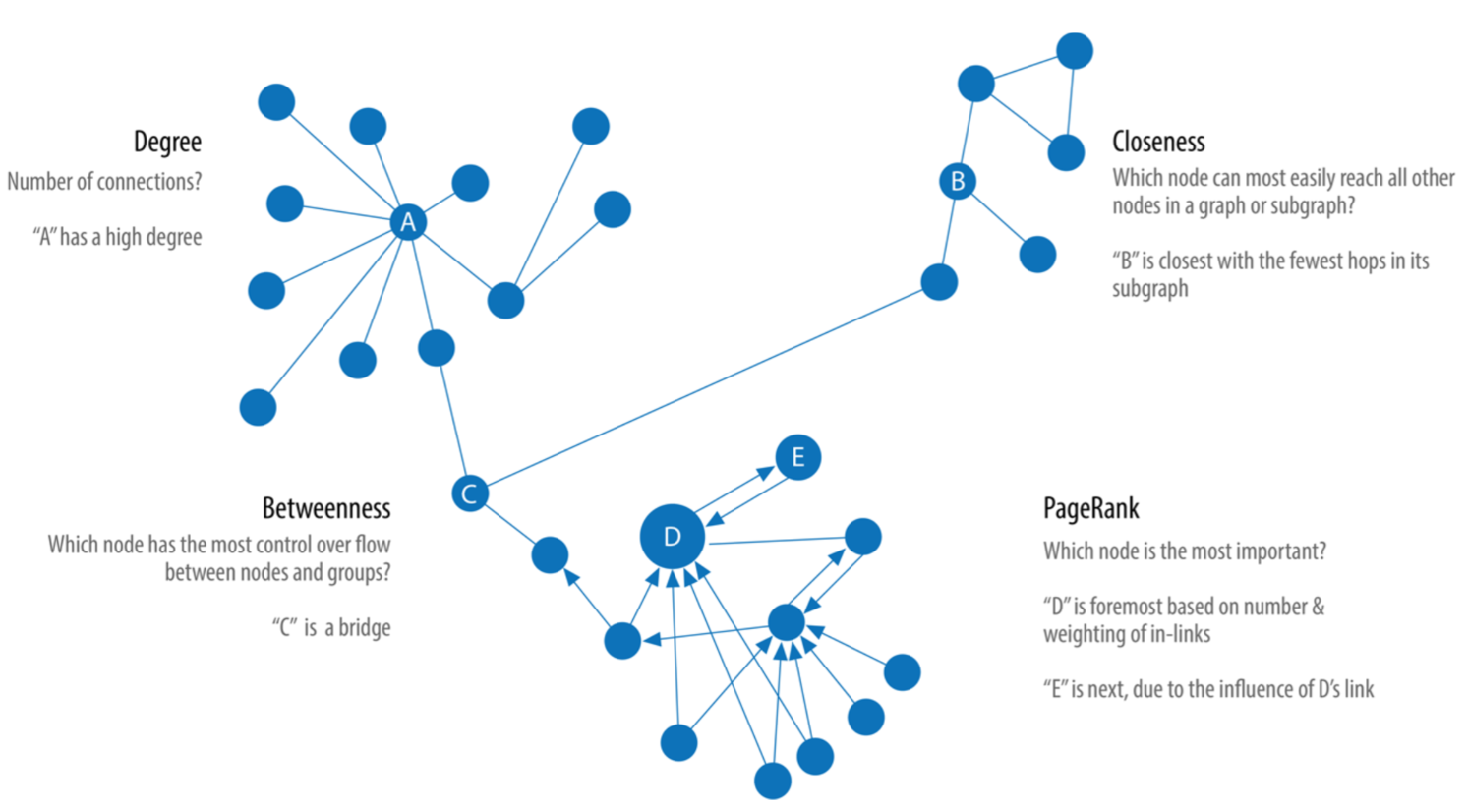
中心性
ある尺度で見たときに、そのノードまたはエッジがどれだけ中心的な(重要な)役割を果たしているかの指標値です。
指標には色々なものがあり、接続性、近接性、離心性、媒介性などが挙げられます。
具体的にどんな中心性があるかは、後ほど紹介していきます。
書籍: O'reilly Graph Algorithms: Practical Examples in Apache Spark and Neo4j より
構造指標
数値データの集合に対して平均や標準偏差といった記述統計量があるように、グラフの世界でもグラフの性質を示すような評価値があります。
例えばごく単純なところだと、グラフの密度、半径、直径、次数の分布 といったものがあります。各種の構造指標を用いることで、そのグラフの特徴を表現することができます。
前出の中心性は、各ノードに注目した指標(点中心性)として語られることが多いですが、構造指標のアルゴリズムではグラフ構造全体に対する指標を求めます。
その他
その他、周囲の関係性からノード間の潜在的なリンクの存在を予測する『リンク予測』といったカテゴリーもあります。 (例: SNSの「〇〇さんと友達ですか?」的なやつ。リンクの予測。)
また近年では、DeepWalk など Deep Learning と絡めたグラフアルゴリズムも登場してきており、機械学習とグラフの親和性について見聞きする機会も多くなってきました。
続いて、グラフデータベース製品(今回紹介するのは、Neo4j と Oracle PGX)が、どんなアルゴリズムを提供しているかを 一口メモ形式で紹介していきます。
Neo4j 組み込みのグラフアルゴリズム
[ The Neo4j Graph Algorithms User Guide ]
https://neo4j.com/docs/graph-algorithms/current/
公式サポートされているアルゴリズム
以下、アルゴリズムの名称は上記のサイトに記載されている名称に従っています。
コミュニティ検出
-
Weakly Connected Components:
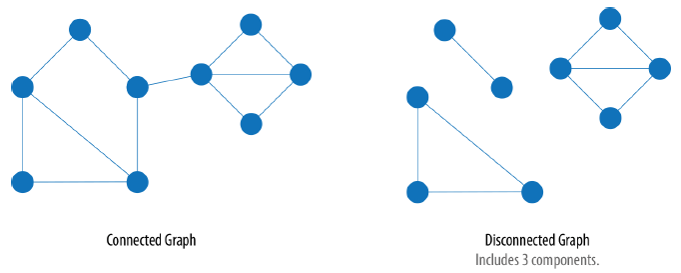
エッジの向きを気にせず、連結2 している極大のサブグラフ(連結成分)を求める。
無向グラフ3の場合、もともとエッジの向きを気にする必要はない。有向グラフ4の場合でエッジの向きを考慮する場合は、後出のStrongly Connected Components を参照のこと。
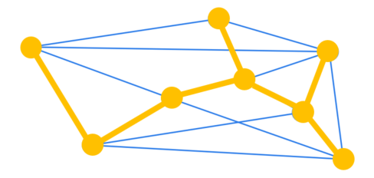
左下図の場合 連結成分は1つ、右下図の場合 連結成分は3つになる。下図のような小さいグラフだと連結成分を見つけることは一見して自明なことに感じるが、大きなグラフの場合、連結成分を識別することは自明ではなく、アルゴリズムの出番となる。
連結成分は、ノード同士の繋がりの強さなどの高度な評価はさておき、最低限 繋がり合っているノード同士という意味ではコミュニティの基礎的な単位と捉えることができる。
書籍: O'reilly Graph Algorithms: Practical Examples in Apache Spark and Neo4j より
-
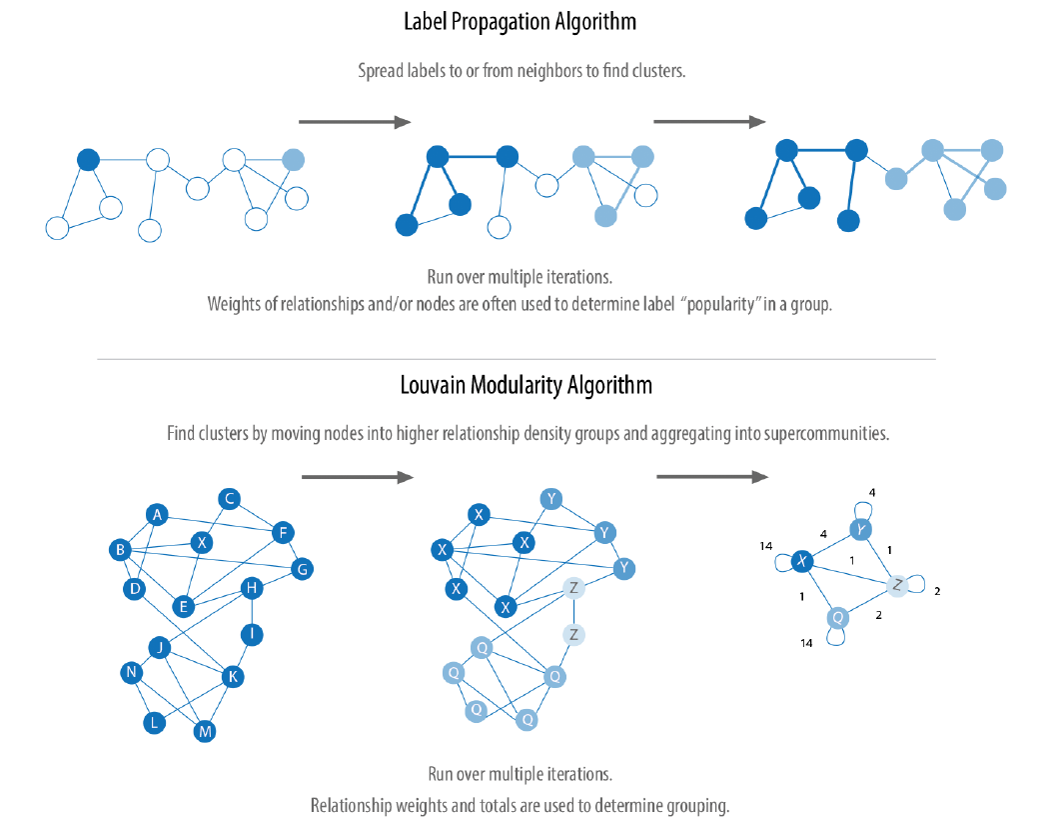
Label Propagation:
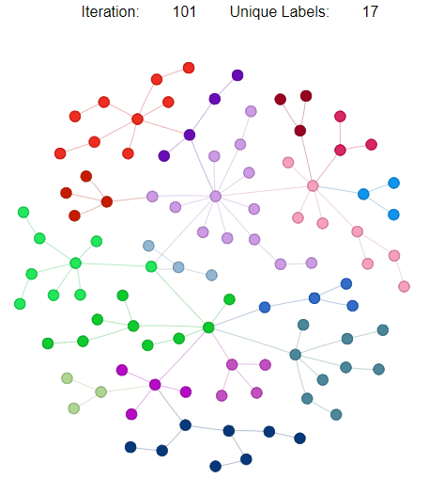
最初に各ノードに一意のラベルを割り当て、エッジ伝いにそのラベルを伝播させていく。
具体的な流れは、あるノードをランダムにピックして、そのノードが隣接しているノード達の中で一番多いラベルを自分自身のラベルとして採択する。つまり、自分の周囲のラベルによる多数決で自分自身のラベルを採択していく。
これを各ノードに対して繰り返し実行していくと、リンク関係にあるノード同士が徐々に同じコミュニティになっていき、ラベルが淘汰されていく。("朱に交われば赤くなる" の様な挙動)
ラベルの変動が無くなる(収束)か、指定したイテレーション回数に到達した時点で終了。最終的に同一のラベルになったノード同士が同じコミュニティに属するという手法。仕組みは至ってシンプル。検出するコミュニティ数を最初に指定するタイプではなく、処理の過程でコミュニティ数が淘汰されていくタイプのクラスタリング。
書籍: O'reilly Graph Algorithms: Practical Examples in Apache Spark and Neo4j より
-
Louvain:
2つの処理フェーズからなる手法。こちらもコミュニティ数は与えなくても、自然と淘汰される。
まず、前出のLabel Propagation 同様に最初に各ノードに一意のラベルを割り当てる。
この状態からフェーズ1 を開始。まず あるノードをランダムを選択して、そのノードが隣接しているノード達のラベルの中から、もし採択したら Modularity(説明は後出。コミュニティ分割の良さの指標値)が一番向上するラベルを自分自身のラベルとして採択する。
これをLabel Propagation と同様に、各ノードに対して繰り返し適用していき、Modularity の向上が収束した時点でフェーズ1 が終了。Label Propagation では周囲のラベルの多数決で自分自身のラベルを決めたが、Louvain では Modularityを指標に決める。この時点で、ひとまず第一段階のコミュニティ分割(同一ラベル同士が同じコミュニティ)がなされる。
次にフェーズ2 を開始。フェーズ1 で同一コミュニティとして括られたノードを仮想的な1つのノードと仮定して、1コミュニティ= 1ノード に集約したグラフを準備。フェーズ2では、この集約した仮想のグラフに対して、同様にノード(コミュニティ)をランダムにピックしては、周囲のノード達のうちModularity の向上が一番見込めるノード(コミュニティ)のラベルを採択していく。こちらも、Modularity の向上が収束した時点でフェーズ2 が終了。以上、Modularity を指標に2段階で階層的(ノード → コミュニティ → コミュニティ同士の融合)にコミュニティを検出する手法。
中心性
-
PageRank:
もともと、Googleの創業者が各Webページ(ノードに相当)の重要度を測る際に考案。
最初に、各ノードに対して等しい得点(重要度のランク)と、ノードとリンク関係を基にした得点の遷移則(後述)を設定する。そして、(ランダムウォークのように)その遷移則のもとで得点を繰り返し遷移させ、最終的に収束した得点でノードの重要度を測る。遷移則として、多くのノードからリンクされるノードや、得点の高いノードからリンクされるノードには高い得点が集まるように設定する。一方でリンクを乱発するノードの1つのリンクからは少ない得点しか移動しない。このような設定のもとで、最終的に高い得点が集まったノードを重要度の高いノードとみなす中心性の指標。
その他 多くのアルゴリズムをラインナップ
上の4つの他にも未だ公式にサポートされていないながらも、非常に多くのアルゴリズムがラインナップされています。
また最短経路のアルゴリズムも、Cypher Query の構文の中に組み込まれています。
[ Neo4j Labs Graph Algorithms ]
https://neo4j.com/docs/graph-algorithms/current/labs-algorithms/
(not officially supported)
※ 今後、Neo4j Labs のアルゴリズムについても調査したいが、、、今回はスキップにて御免。
Oracle PGX 組み込みのグラフアルゴリズム
[Oracle PGX Built-In Algorithms]
https://docs.oracle.com/cd/E56133_01/latest/reference/analytics/builtins.html
以下、アルゴリズムの名称は上記のサイト記載されている名称に従っています。
(カテゴライズは私の方で、多少 アレンジしています。)
グラフ探索・経路探索
-
Graph Traversal Algorithms:
指定されたノードを起点に、幅優先探索5 または 深さ優先探索6 を用いて与えられた深さまでノードを単純に探索する。ノードに対するフィルター条件なども指定可能。探索して訪れたノードには起点からの深さを記録する。つまるところ、幅優先探索・深さ優先探索を実行するアルゴリズム。 -
Reachability Algorithms:
2つのノード間(始点ノードと目的ノード)を指定したホップ数7 以内で到達できるか否かを求める。実装としては、始点ノードから幅優先探索を実施して、指定した深さ以内で目的ノードを見つけることができるかで判定している。 -
Dijkstra Algorithms:
ダイクストラ法8で最短経路(経路上のエッジの重み9 の和が最小の経路)を求める。後出のBellman-Ford 法より効率がよいが、重みに負の値が含まれている場合は適用できない。 -
Bidirectional Dijkstra Algorithms:
双方向探索10にダイクストラ法を適用して最短経路を求める。従来のダイクストラ法の様にスタート地点から逐次的に経路を確定するだけでなく、ゴール地点からもスタート地点に向けて同時に経路を探索することでトータルで探索コストを抑えて最短経路を求める。スタート地点だけから探索すると、ゴールに至るまでの探索範囲が広くなりがちだが、ゴール地点からも同時に探索することで双方の探索が重なったときに経路を特定できる。最悪のケースでの探索コストは従来の探索と同じだが、実用上 従来より良いパフォーマンスとのこと。 -
Bellman-Ford Algorithms:
ベルマン–フォード法11で最短経路(経路上のエッジの重み9 の和が最小の経路)を求める。重みに負の値が含まれていても適用可能。但し、重みの総和が負となる閉路がある場合は適用不可。重みの総和が負の閉路がある場合、それをひたすらグルグルしておけばよいので最短経路が求まらなくなる。 -
Hop Distance Algorithms:
エッジの重みは利用せずに、ホップ数7 をもとにした最短経路を求める。
言い換えると、エッジの重みを一律 1 とみなしたときの最短経路でもある。 -
Fattest Path:
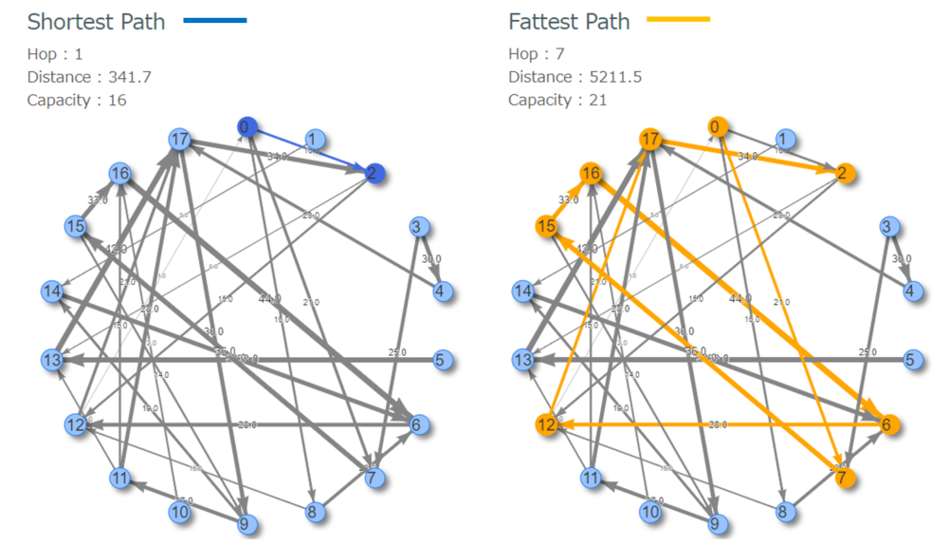
最短経路ではなく、最大流経路(経路上に登場するエッジの重み9 の最小値が最大の経路)を求める。距離ではなく 幅に関心があるときに利用。例えば、距離として多少 遠回りしてもいいから幅が太くて最大限の物を運べる経路を確保したいときなどの用途。
[ サンプル: ノード0 → ノード2 への最短経路・ホップ数・最大流経路の比較 ]
※ 見えにくいが、エッジ上の数値がCapacity(幅)。Distanceは平面上の距離。
-
Prim's Algorithm:
最小全域木12 (グラフの全ノードを繋ぐ木のうちで、エッジの重みの総和が最小の木)を求める。前出までの出発地-目的地のような2ノード間の経路探索ではなく、全ノードを結ぶ上での最短経路を求める。
コミュニティ検出
-
Weakly Connected Components (WCC):
Neo4j の節での前出の通り。 -
Strongly Connected Components:
有向グラフ4 において、エッジの向きを考慮した上で連結2 している極大のサブグラフ(連結成分)を求める。Weakly Connected に、"エッジの向き" という条件が加わっている。エッジの向きを考慮した連結成分を求めるときは、こちらを利用する。 -
Conductance Minimization (Soman and Narang Algorithm):
前出のLabel Propagation の類似アルゴリズム。Label Propagation ではラベル採択の際に多数決(自分と隣接するノード達が持つラベルで一番多いもの)を利用していたが、当該アルゴリズムでは単純な多数決ではなく、トライアングルの数に関係する重みでラベルを採択する。
トライアングルの数え上げについては、後出のTriangle Counting、Local Clustering Coefficientを参照のこと。実際にLCC と似た数値でエッジに重みづけを行い、その重みをラベル採択時に活用している。これにより、自分との繋がりがより強いラベルを優先的に採択するようになる。 -
Infomap:
※ すみません、現在 理解が追い付いていません。アルゴリズム自体はコミュニティ検出のアルゴリズムで、最終的に得られるものは 各ノードへ割り当てられるコミュニティID になる。 -
Matrix Factorization:
グラフを利用したマッチングのアルゴリズム。
ショッピングサイトのレコメンドエンジンのように、ユーザーのノード集合と、商品アイテムのノード集合からなる2部グラフ13を定義する。単純にユーザーとアイテムの隣接行列を作成しても、巨大でスパースな隣接行列になるだけなので、このアルゴリズムでは、最急降下法を利用してユーザーとアイテムの各ノードに対して次元数を抑えた特徴ベクトルを生成していく。(すみません、ここの特徴ベクトルの作成の仕方は理解が追い付いていない。。)
ひとたび特徴ベクトルを作成すると、ある一人のユーザーの特徴ベクトルと、ある1つのアイテムの特徴ベクトルの内積をとることで、マッチングのスコアが算出できるという仕組み。
あとは、あるユーザー1人を固定して全アイテムに対する内積を取れば、その人に合う商品アイテムのスコアがずらりと分かる。各ノードに対して、特徴ベクトルを埋め込むのが特徴的な手法。
中心性
-
Closeness Centrality Algorithms:
近接中心性。「自ノード」と「自ノード以外の全ノード」との距離の総和の逆数。
距離総和の逆数なので、他の皆からの距離が近くて全体の中心的な位置にいるほど高くなる指標。逆に隅っこに位置して、他の皆からも総じて距離が遠いノードは、相対的に値が低くなる。グラフの中において、皆から平均的に近いノードはどのノードかに相当する指標なので、大勢の人との待ち合わせ場所を平等に決めるのには向いている指標かも... -
Degree Centrality Algorithms:
次数中心性。単純に当該ノードに何本のエッジが接続されているかの指標。
また、次数の大きいノードのことを"ハブ"と呼ぶ。多くの方面との路線を運航する空港をハブ空港というが、それと同じ意味合い。SNSにおけるインフルエンサーは多くの次数を有しており、鉄道路線においては新宿駅などが多くの次数を有している。次数が多いノードはネットワークに対して強い影響力を持っており、それだけ注目に値するノードとなる。
逆に言うと、悪意を持った攻撃の対象にもなりやすい。ネットワーク上のノードをランダムに攻撃するより、次数の高いノードから順番に攻撃したた方がネットワーク全体が麻痺しやすい。
(※ 詳しくは参考書籍の『複雑ネットワーク』を参照のこと。) -
Eigenvector Centrality:
固有ベクトル中心性。次数中心性を拡張した指標。次数中心性では単に当該ノードだけの次数だけに着目していたが、固有ベクトル中心性は周囲のノードの次数も加味した上で中心性を定める。つまり、仮に自分自身の次数は少なくても周囲のノードの次数が高い場合は、自身の中心性としては高く評価される。
固有ベクトル中心性の例えとして(例えとして妥当かどうか自信はないが...)
多くのファンを持つ有名歌手 ジャスティン・ビーバー氏が、ピコ太郎氏を紹介したことでピコ太郎氏の注目度が一気に上昇した。言い換えると、多くの次数を持つノードからのリンクが発生したことで、次数の少ないノードであっても中心的なノードになった。これは前出の次数中心性や、後出の媒介中心性だけでは捉えられない事象。
固有ベクトル中心性の求め方は、隣接行列の固有ベクトルを求めることで得られる。但し、非連結や非強連結のグラフに適用しにくいという側面があり、それらに対応を施した1つが前出のPageRank(Damping Factor の適用) でもある。 -
Vertex Betweenness Centrality Algorithms:
媒介中心性。自ノード以外の任意の2ノード間の最短経路候補上に、自ノードが何回登場するかで決まる指標。自ノード以外のノード間を結ぶ最短経路上に登場する回数が多いほど高くなる。グラフの中のノードを当ノードがどれだけ中継(媒介)しているかの指標となる。また、仮に当ノードがグラフから失われた場合、残されたノード間の最短経路の構成に大きな影響(東西で分裂が発生するなど)を与えるため要所となるノード。
前出の次数中心性との関係でいうと、次数中心性と媒介中心性は必ずしも相関するとは限らない。ハブとして高密度ではあるが最短経路上にそのハブが多く登場するとは必ずしも限らないし、逆も然り。 -
PageRank Algorithms:
Neo4j の節での前出の通り。
PGX では従来のPageRankに加えて、Weighted PageRankや、Personalized PageRank も利用可能。従来のPageRank では、ページやリンクについて重要度の偏りを持たせず公平に初期化する。一方、Weighted PageRank では各リンクに対して重要度の重みづけを設定する。また、Personalized PageRank は特定のノード(重要なページ)に対してあらかじめ高いランクを割り当てる。Weighted PageRank はリンクに対して、Personalized PageRank はノードに対して、重要度の設定にあらかじめ偏りをつけて調整した PageRank の手法 。 -
Random Walk with Restart:
ランダムウォーク。指定された起点ノードから指定された回数分だけランダムウォークを繰り返す。
あるノードから複数のエッジが伸びている場合、それらのエッジを等確率で選択して接続先のノードに移動する。行き止まりのノードに到達した場合は、あらかじめ指定された確率で起点ノードにワープする。以上を指定回数だけ繰り返して、各ノードには訪問回数を記録する。起点ノードから到達しやすいノード(関係性の強いノード)ほど、確率的に訪問回数が多くなる。 -
Hyperlink-Induced Topic Search (HITS):
※ すみません、現在 理解が追い付いていません。 -
Stochastic Approach for Link-Structure Analysis (SALSA) Algorithms:
※ すみません、現在 理解が追い付いていません。
構造指標
(補足)
以下の構造指標の中でコミュニティ構造に関する指標も登場するが、それらの指標はあくまで既に各ノードに対してコミュニティのラベルリングがされているグラフが前提となる。
よって、前出のコミュニティ検知のように、これから未知のコミュニティを求めるためのアルゴリズムではない旨を補足しておく。どちらかというと、コミュニティ検出のアルゴリズムの中でコミュニティを導出する際に、構造指標を用いる。(Louvain の中で Modularityを利用。)
-
Degree Distribution Algorithms:
ノードの次数のヒストグラムを求める。グラフ内のノードの次数の分布が分かる。
スケールフリーネットワーク14の様に一部の少数のノードの次数が非常に高くて 大多数のノードの次数が低い分布や、ランダムネットワークのように次数がポアソン分布に従うようなケースなど、グラフが対象とするドメインの違いによって特徴的な分布を取り得る。現実世界にある様々なネットワークもスケールフリー性を有していることが多い。インターネットもその1つ。この辺りの話は私の拙い文章なんかよりも複雑ネットワーク関連の参考書籍に興味深く描かれている。 -
Cycle Detection Algorithms:
閉路15 の存在有無を求める。 -
Eccentricity Algorithms:
各ノードの離心数とグラフの直径・半径を求める。離心数とは、自ノードから一番離れたノードへの距離である。グラフの中で最も離れた2点の距離(全ノードの中で最も大きい離心数)をグラフの直径という。
当アルゴリズムの実装とは直接関係ないが、離心数の逆数を指標値にした離心中心性という中心性指標もある。近接中心性と似ているが、近接中心性は平均的な近さに対して、離心中心性は一番遠いノードでもどれくらい近いかを示している。近接:Average距離 の近さ、離心:Max距離 の近さ という違いがある。 -
Triangle Counting:
グラフの中に存在するトライアングル16の全数を数え上げる。トライアングルの数え上げは、次項のLocal Clustering Coefficient (LCC) にも関係ある数値。
トライアングルがあるということは、友達の友達とも、また友達という関係が成り立っておりその周囲で強い繋がりが形成されている兆しにもなる。ただ、三角形ではなく四角形の繋がり(友達の友達の友達とも、また友達)でもいいわけだが数え易さ的に三角形の方が数えやすく採用されることが多い。
(詳しくは、参考書籍の『複雑ネットワーク 基礎から応用まで』にて言及されている。) -
Local Clustering Coefficient (LCC)
各ノードに対して、そのノードを含むトライアングルの数をもとにした係数を算出する。
ノードv の次数をk とすると、ノードvを含むトライアングルの数の理論的最大値は、k * (k-1) / 2 になる。ノードv のLocal Clustering Coefficient とは、以下の値。
ノードv の LCC = ノードvを含むトライアングルの数 / (k * (k-1) / 2)
つまり、ノードv を含むトライアングルの数を先ほどの理論的最大値で割ったもので、ノードv の周りにどれくらいの割合でトライアングルが発生しているかになる。なぜトライアングルを利用するのかについては、前項で触れている。 -
K-Core:
k-coreとは、どの頂点も次数がk以上からなる極大の連結サブグラフである。もし、比較的にkの大きいk-coreが存在したら、そこは次数が高いノード同士が連なっている状態となっている。ある種、金持ちの知り合いもまた金持ちみたい構造となっている。実際にリッチクラブ係数なるものもある(詳しくは、参考書籍の『Pythonと複雑ネットワーク』に言及があります)。k-coreは単純に次数だけを評価しているので、同じ k-coreに所属しているノード同士がお互いに高密度で繋がっているかもしれないし、そうではないかもしれないが、一定の次数以上のノードが連なっているというのは、周囲とは異なる構造の1つとして捉えることができる。 -
Conductance:
コミュニティ構造に対する指標。あるコミュニティが内側に閉じているか、外側に開いているかの相対的な指標。評価方法はシンプルで、対象のコミュニティが持っている全リンクの合計数と、対象のコミュニティから異なるコミュニティへのリンクの合計数の比率で表現される評価値。異なるコミュニティとのリンクの割合が多いコミュニティは、評価値が高くなる指標設計。
Conductanceに相当する日本語訳が分からないが、、ぱっと調べた限りでは " 回路における電流の流れやすさ " とあり、コミュニティ間における情報の流れやすさと捉えればよいのかな!? -
Partition Conductance:
前出のConductance をグラフ全体に拡張したアルゴリズム。前出のConductance はある1つのコミュニティに対して算出した値になるが、Partition Conductance は、Conductanceの計算を全コミュニティに適用して、そのConductanceの総和をコミュニティの数で割ったもの。つまり、グラフ内に存在する各コミュニティのConductance の総和平均に相当する。 -
Modularity:
コミュニティ分割の良さの指標。Q値とも呼ばれる。コミュニティ検出の評価の際によく用いられる指標。
同一コミュニティ内は密結合で、コミュニティ外とは疎結合の構造ほど評価値が高くなる指標設計。システムのアーキテクチャやソースコードの"モジュール"とも通ずるところがある。具体的には、同一コミュニティ内のノード同士を結ぶエッジの割合が相対的に多く発生しているかを比較した値となっている。PGX の当該アルゴリズムの実装は有向グラフを想定したものとなっている。 -
Topological Ordering Algorithms:
DAG17 において、ノード間の依存関係(エッジの向き)を保ってノード集合をソートする。最終的に求まるものは、ソート済みのノードの配列。
例えば、ノードをタスク、エッジをタスクの依存関係だとみなすと、ノードA → ノードCへのエッジは、タスクC を実行するにはタスクA の完了を待ってからという依存関係をグラフとして表現できる。このように依存関係を表現したグラフに対してトポロジカルソートを実施すれば、どの順序でタスクを実行すれば依存関係を必ず保って全タスクを実行できるかが求まる。
リンク予測
-
Adamic-Adar index:
もともとSocial Networksを対象に、2人のユーザーの間にリンク(友人関係)が潜在的に存在するか否かの予想をする際に提案された指標。基本的には共通の友人が多いほど高くなる指標だが、例えば 有名人(不特定多数の人との間にリンクがあるようなノード)を介したような繋がりに対してはあまり高く評価しないことで、その2人の間に実際に直接的な友人関係があるかを予想する。 -
WTF (Whom To Follow) Algorithm:
※ すみません、現在 理解が追い付いていません。
まとめ
以上、グラフデータベース(Neo4j, Oracle PGX)に組み込まれているグラフアルゴリズムについて、一口メモ形式でざっとご紹介しました。(説明の絵や式が少なくて、すみません。説明の不備などありましたら、ご指摘下さい。)
また、今回 Neo4j や PGX を中心に紹介しましたが、他のグラフデータベースとしては TigerGraph にもグラフアルゴリズム用のテンプレート(サンプルコード)が準備されています。
ご参考までに下記リンクを載せておきます。
TigerGraph
ではでは。
参考書籍
-
O'reilly Graph Algorithms: Practical Examples in Apache Spark and Neo4j
https://neo4j.com/graph-algorithms-book/ -
ネットワーク分析 Rで学ぶデータサイエンス 8
https://www.kyoritsu-pub.co.jp/bookdetail/9784320113152 -
複雑ネットワーク 基礎から応用まで
https://www.kindaikagaku.co.jp/information/kd0363.htm -
ネットワーク科学の道具箱
https://www.kindaikagaku.co.jp/information/kd0346.htm -
Pythonと複雑ネットワーク
https://www.kindaikagaku.co.jp/information/kd0602.htm
-
DB-Engines: https://db-engines.com/en/ranking/graph+dbms ↩
-
ダイクストラ法: https://ja.wikipedia.org/wiki/ダイクストラ法 ↩
-
ベルマン–フォード法: https://ja.wikipedia.org/wiki/ベルマン–フォード法 ↩
-
トライアングル: 異なる3ノードを結ぶ長さ3の閉路。 ↩
-
DAG(有効非巡回グラフ): https://ja.wikipedia.org/wiki/有向非巡回グラフ ↩