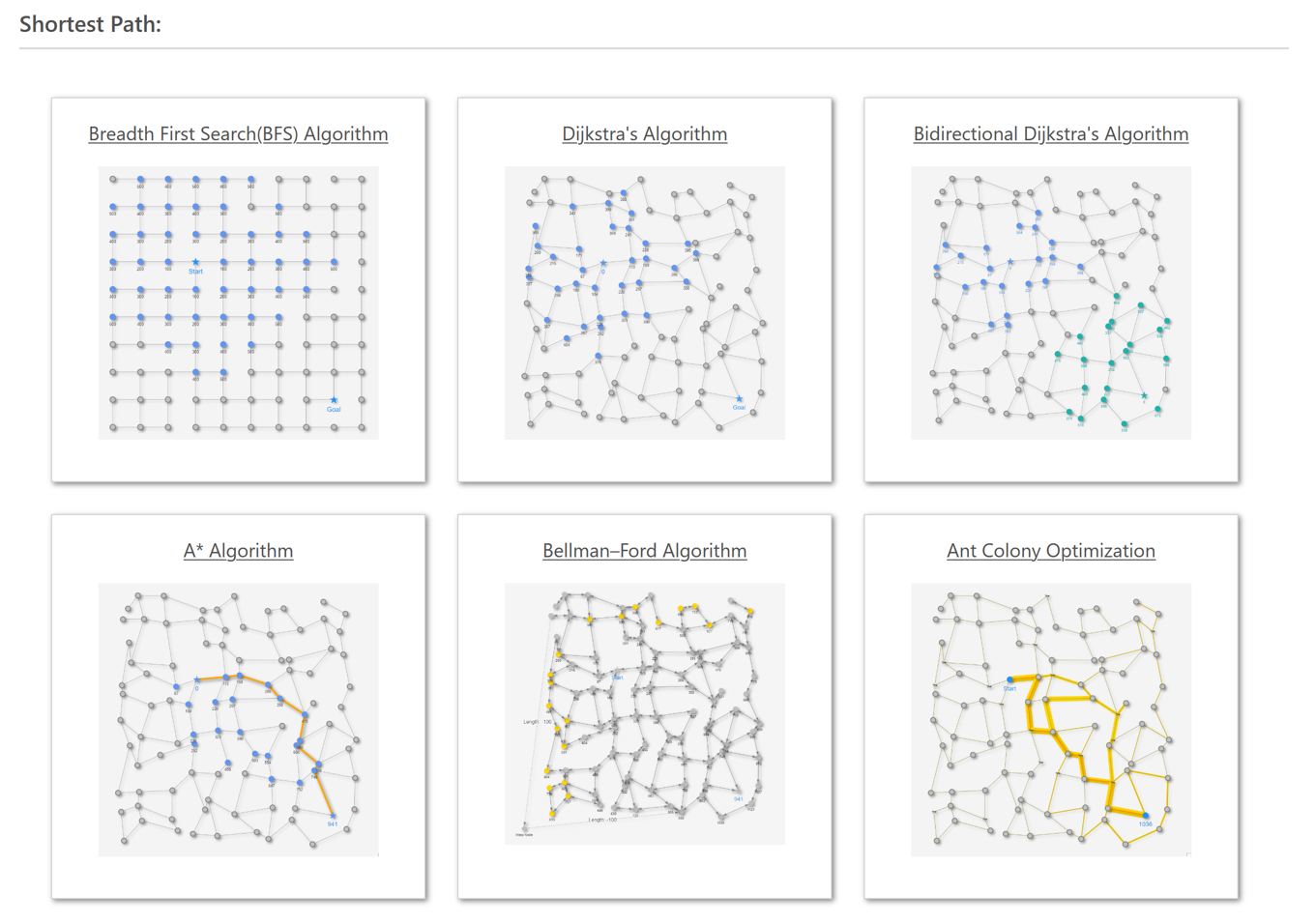
はじめに
UL Systems Advent Calendar 2020 - 20日目。
当記事では、2点間(単一始点-単一終点)の最短経路アルゴリズムについて紹介していきたいと思います。
最短経路アルゴリズムというとグラフ理論に属する話になりますが、当記事ではそういった込み入った話はさておき、単純に与えられた迷路に対してStart地点からGoal地点までの2点間の最短経路を求める過程を視覚的に楽しむぞ!をモットーに説明していきます。また、一口に2点間の最短経路アルゴリズムと言っても多くの手法が存在します。それぞれの最短経路アルゴリズムの特徴について紹介していきたいと思います。
当記事で紹介する最短経路アルゴリズムのリストは以下です。順々に紹介していきます。
- 幅優先探索
- ダイクストラ法
- 双方向ダイクストラ法
- A* 法
- ベルマン-フォード法
- Ant Colony 最適化
当記事で使うもの
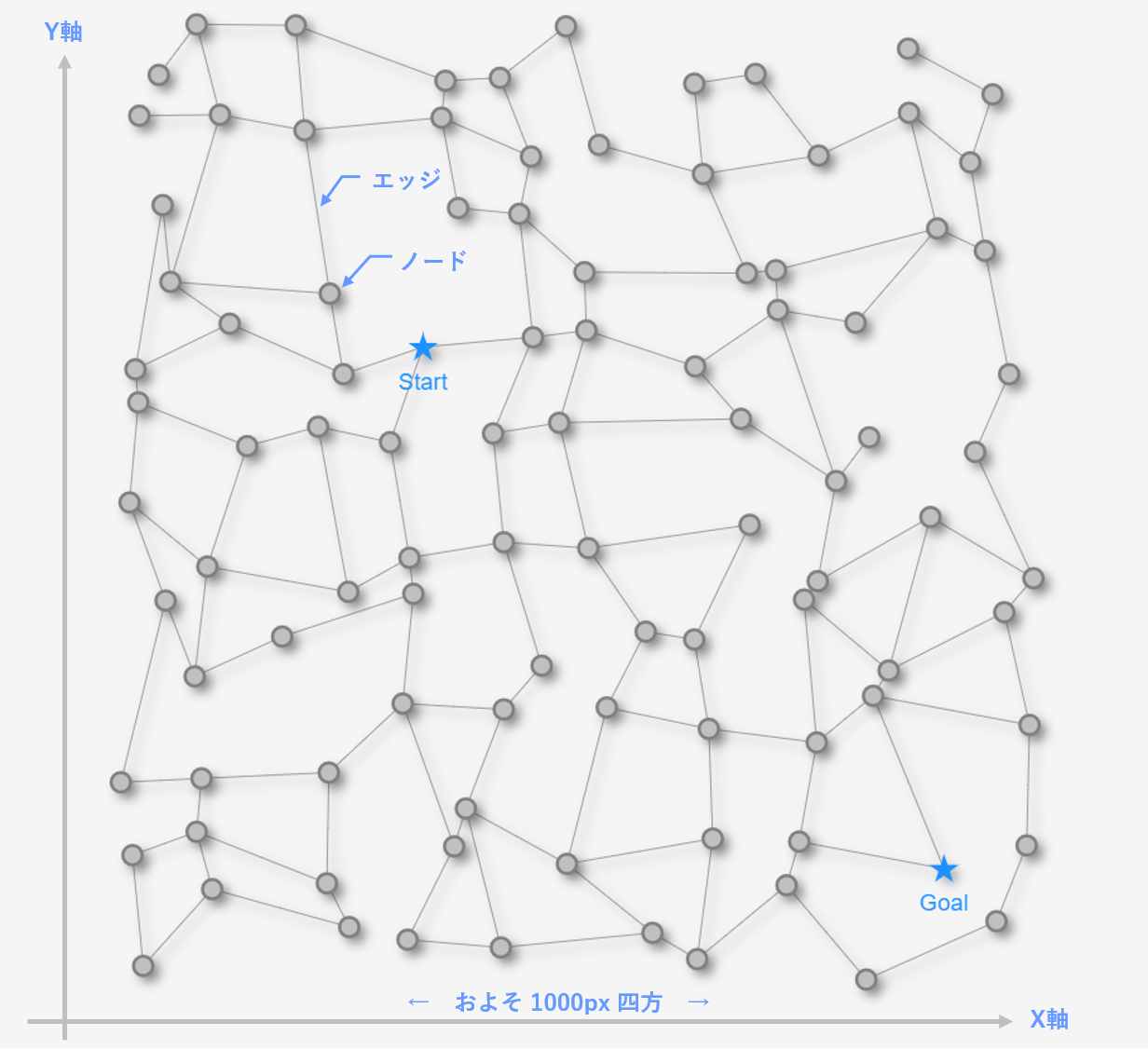
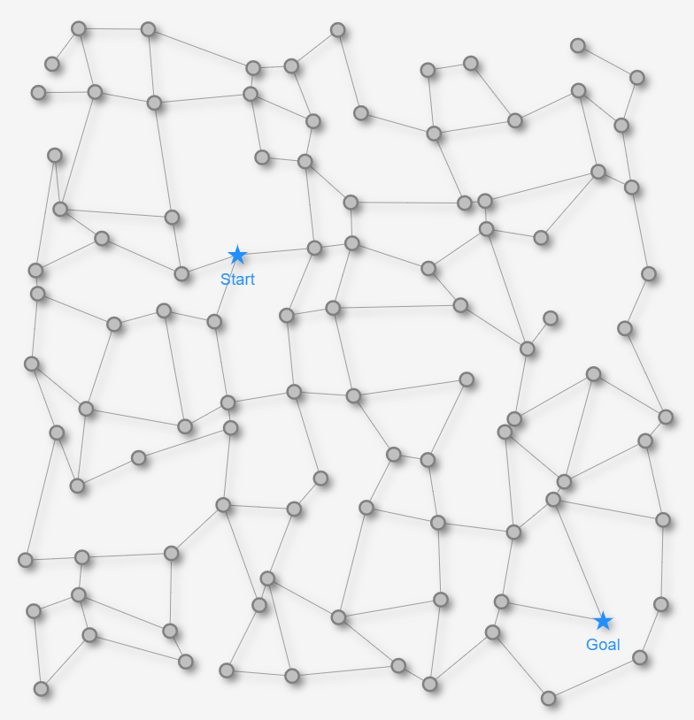
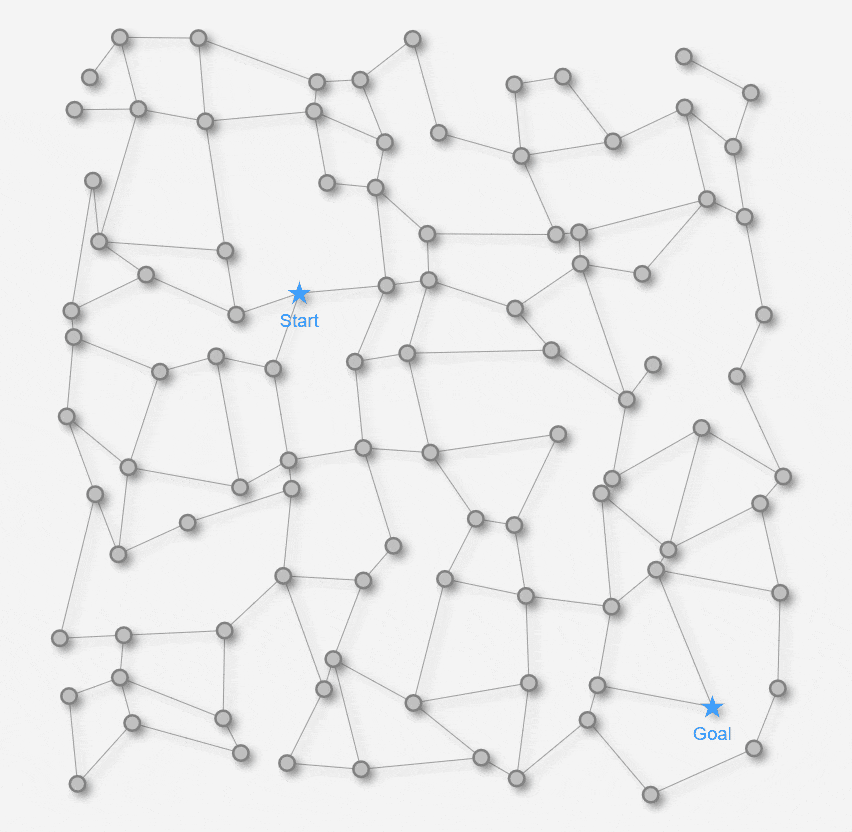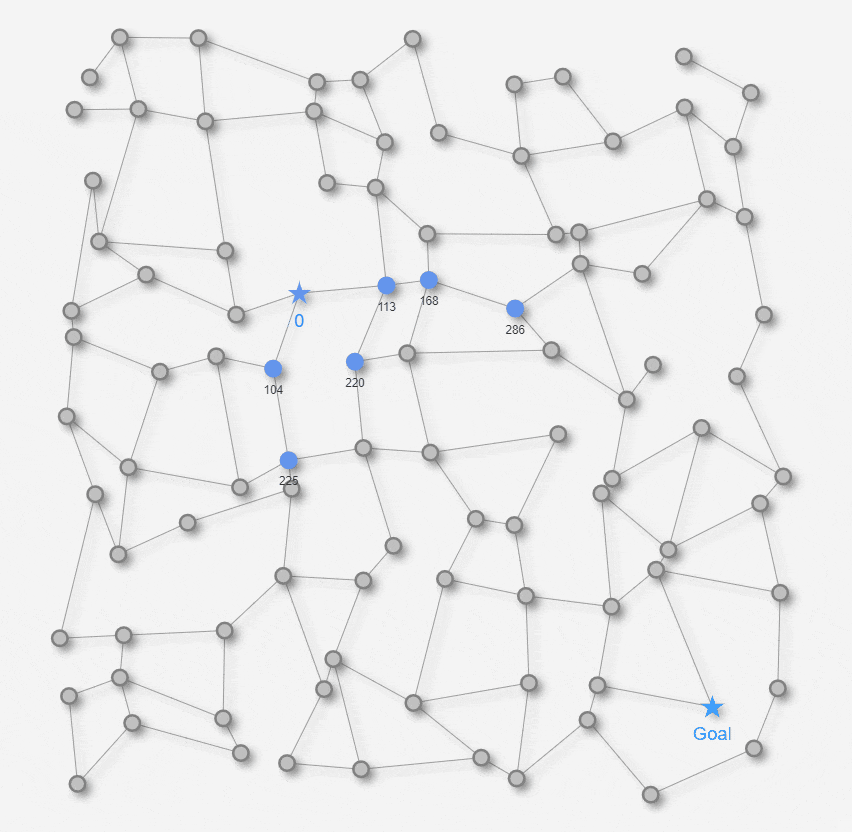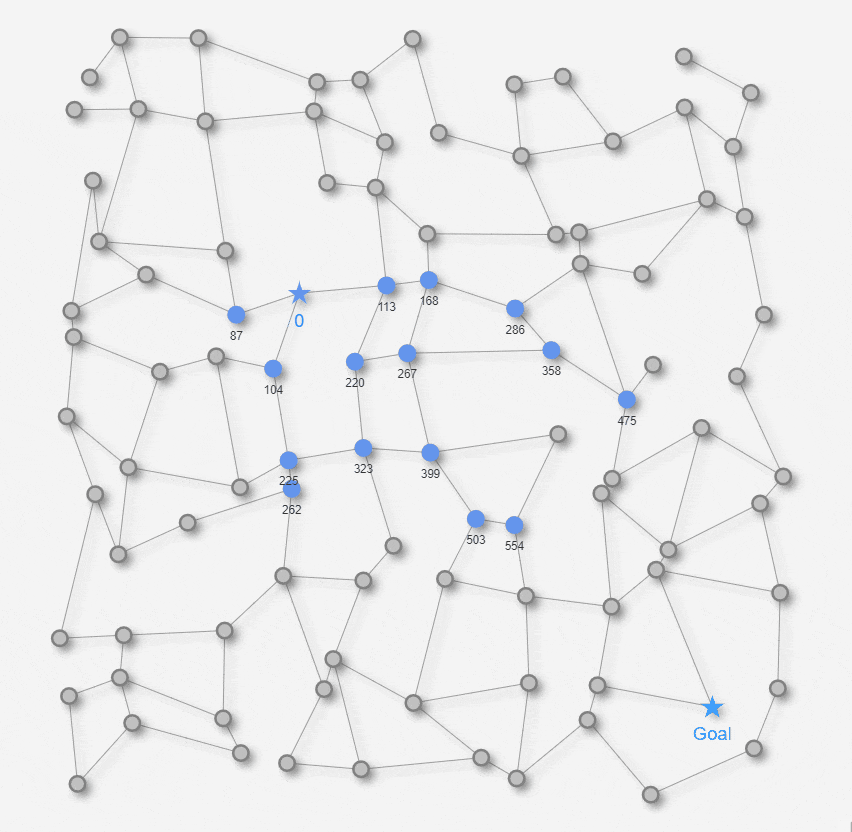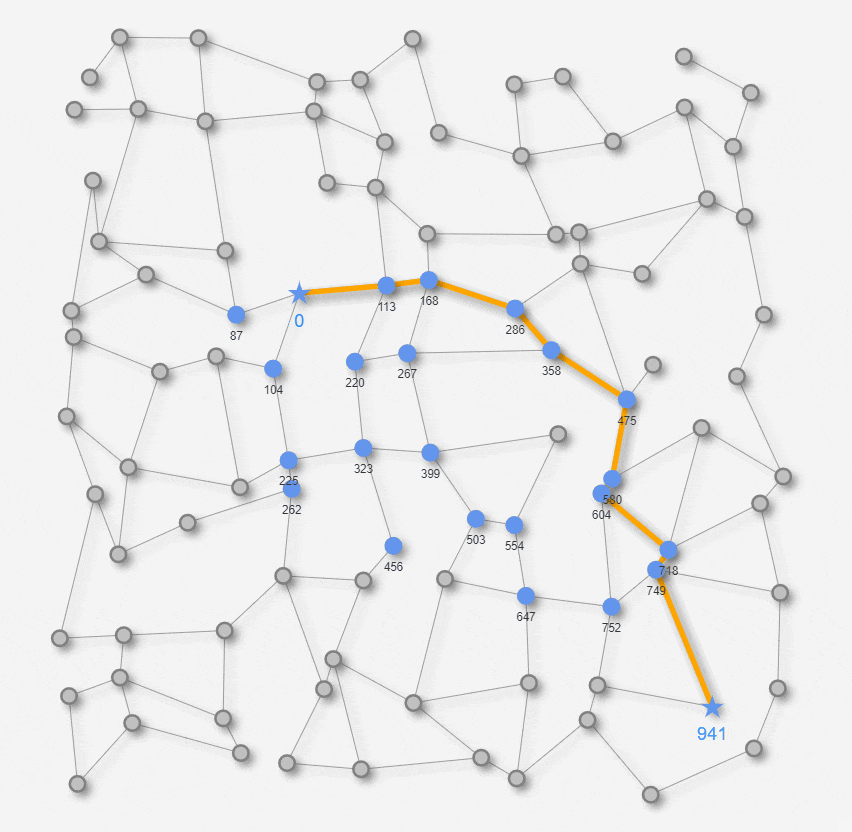
最短経路を求める舞台となる「迷路」として、以下の2種類の迷路を用意します。
いずれも約1000px 四方の平面の迷路です。★マークのStart地点から★マークのGoal地点を目指します。
以降の記事の中で使う用語・前提は、以下になります。
- ノード: 上の迷路の **●マーク をノード(頂点)**と呼ぶことにします。
- エッジ: 上の迷路の **●マーク と ●マークを結ぶ線をエッジ(辺)**と呼ぶことにします。
- エッジの長さ: 今回 平面上の迷路を利用しているので、エッジの両端ノード間の距離とします。当記事での距離は、ピクセル上のx座標とy座標を基準にしたユークリッド距離とします。また、当記事では特記がない限りはエッジの長さは0以上を想定します。
- エッジの通行の向き: 当記事の迷路は特記がない限り、エッジは相互通行とします。つまりエッジの両端ノードのどちらからでも、もう片方へのノードに進むことが出来ます。逆に一方通行のエッジが登場する際は明記します。
- 最短経路: StartノードからGoalノードを結ぶ経路上のエッジの長さの総和が最小になる経路 のことを指します。今回の迷路は見ての通り StartノードからGoalノードへは到達可能であることを前提として、到達できないケースのハンドリングは省略します。
以降の記事の中で登場するアルゴリズム・可視化のコードは、以下になります。
-
言語: TypeScript
-
可視化用ライブラリ: vis-network
また、各アルゴリズムのステップを可視化したGIFアニメーションを挿絵として入れています。
記事の文章より、そちらを見ていただけるとイメージが掴みやすいかもしれません。
参考にさせていただいた資料
-
データ構造とアルゴリズム
https://www.kyoritsu-pub.co.jp/kenpon/bookDetail/9784320120341 -
アルゴリズム図鑑 絵で見てわかる26のアルゴリズム
https://www.shoeisha.co.jp/book/detail/9784798149776 -
進化計算アルゴリズム入門 生物の行動科学から導く最適解
https://www.ohmsha.co.jp/book/9784274222382/ -
Neo4j: Path finding algorithms
https://neo4j.com/docs/graph-data-science/current/algorithms/pathfinding/ -
Oracle PGX: Built-In Graph Algorithms
https://docs.oracle.com/cd/E56133_01/latest/reference/analytics/builtins.html
それでは本題へ。
幅優先探索
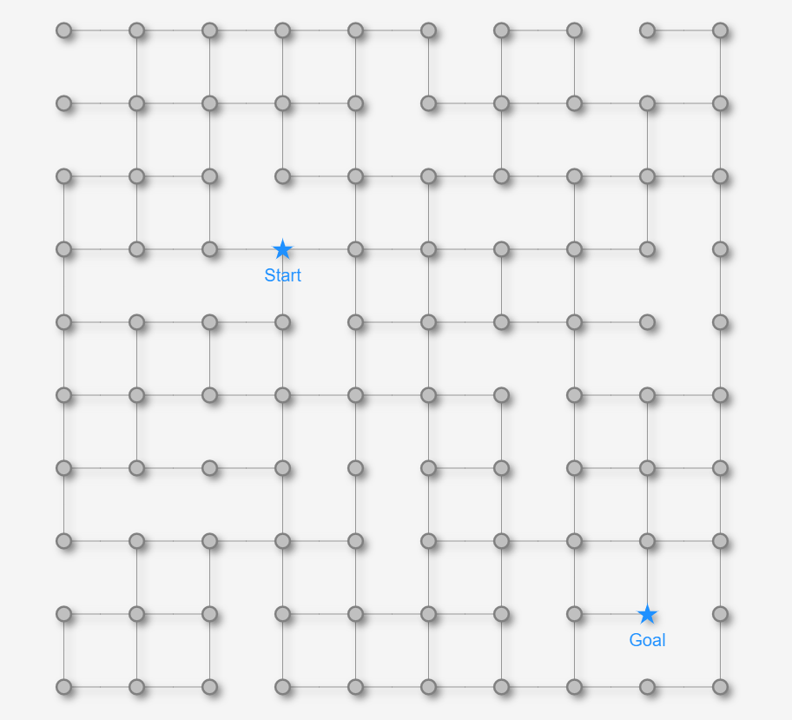
最初に紹介するのは幅優先探索アルゴリズムです。幅優先探索アルゴリズム自体は最短経路専用のアルゴリズムというよりかは、全ノードを網羅的に探索したり、ノード間の到達可能性(Reachability)を判定したりするのに利用されるアルゴリズムです。しかし、ある条件下では最短経路問題にも適用できます。その条件とは全てのエッジの長さが同一のケースです。例えば、下記のような格子状の迷路を考えます。このケースで幅優先探索のアルゴリズムを適用してみます。
この迷路の場合、エッジの長さは全て等しいのでStarノードからGoalノードに至るまでの経路に登場するエッジの数(※ 以降、経路上のエッジの数をホップ数と呼ぶことにします。)が最も少ない経路を見つければ、それがイコール最短経路になります。幅優先探索アルゴリズムを利用して最短経路を見つける流れが次になります。
1. 以下の初期化を行う。
1-1. キューQ を空にする。
1-2. 全ノードを "未探索"のステータスにする。
2. Startノードを キューQ に追加する
3. キューQ が空でない限り、以下の探索処理をループ。
3-1. キューQ からノードu を取り出す。 (※ 初回は Startノードがノードu に該当する。)
3-2. ノードu に隣接している全ての "未探索" ステータスのノードv に対して、以下を実施。
(1) ノードv に対して、以下の設定を行う。
• ステータスを "探索済み" に変更。
• "経路元ノード" として、ノードu を設定。
(2) ノードv が Goalノードの場合:
探索終了して4. へ。
(3) ノードv が Goalノードでない場合:
ノードv を キューQ に追加して、3. のループを継続。
4. Goalノードから順々に経路元ノードを辿る経路(終着はStartノード)を
最短経路として出力。
流れを簡単に説明します。探索のメイン処理は上記 3. のループ処理です。3.のループ処理の初回ループは、3-1. のノードu としてStartノードが取り出されます。そして、3-2. でStardノードを起点に隣接している全ノードを探索します。これらのノードはStartノードから1ホップで到達できるノードとしてキューに追加されます。キューに追加された1ホップのノード達は、3.のループ処理の過程においてどこかのタイミングで(3-1.のノードuとして)取り出されます。そこで取り出さたノードから隣接している未探索のノードはStartノードから2ホップで到達できるノードとしてキューに追加されます。これを繰り返していき Nホップ目でGoalノードが見つかれば、StartノードからGoalノードまでは 最短 Nホップで到達できるということになり、この時点で探索を打ち切ります。待て待て、Nホップ未満の経路が後から見つかる可能性があるじゃないかと不思議に思うかもしれません。しかし 幅優先探索の場合、1ホップ到達ノード、… 2ホップ到達ノード、 …、Nホップ到達ノード の順に追い越すことなく各ノードがキューQ に追加されていくので、仮に Nホップ未満の経路が存在すれば 既に探索済みノードになっています。
まとめると、Startノードを起点に同心円状というか、渦巻き状に探索エリアを広げていってGoalノードが見つかり次第 ホップ数と経路を確定させます。まるで潜水艦映画に出てくる敵艦を探索するソナーのようなイメージです。ソナーと言われても…と思うので、実際に幅優先探索アルゴリズムの動きをGIFアニメで見てみましょう。
上のアニメでは、"探索済み" のステータスになったノードが青色に変わります。Startノードを起点に渦巻き状に青色が広がっていく様子が見て取れます。ノードの下側に表示される数値がStartノードからの距離(ホップ数 × 100px)になります。最終的にGoalノードが青色に変われば最短経路が確定してオレンジ色の線で最短経路を表示します。以上が幅優先探索のアルゴリズムの動きになります。
余談ですが、探索アルゴリズムには幅優先探索以外に 深さ優先探索 というアルゴリズムもあります。こちらは、言うならば行き止まりにぶつかるまで真っすぐ探索して行き、行き止まりに出くわすと直前の分岐点まで戻って未だ探索してない方の分岐ルートを同様に行き止まりに出くわすまで探索するというのをひたすらに繰り替えします。さながら、家庭用のあのお掃除ロボットのような動きでしょうか(あくまで、個人の感想です)。幅優先探索が渦巻きの様に広がって探索していくみたいなのに対して、深さ優先探索は一点突破をひたすら繰り返しながら1つ1つ潰していくような探索イメージです。
幅優先探索 まとめ
-
エッジの長さが全て等しい場合に適用可能。
-
最短距離というか、最短ホップ経路を見つけ出す。
ダイクストラ法
幅優先探索アルゴリズムが適用できるのは、あくまで先ほどの格子状グラフみたいに全てのエッジの長さが同一というケースに限られます。当然 世の中そのような問題設定ばかりではなく、むしろエッジの長さが様々であるケースの方が普通でしょう。では 以下の迷路ように各々のエッジの長さが異なる場合は、どうやって最短経路を求めればいいでしょうか?
こういった場合に適用できる有名な最短経路アルゴリズムとしてダイクストラ法があります。ダイクストラ法はエッジの長さがそれぞれ異なっていても、長さが非負の値でさえあれば適用できます。(逆に エッジの長さがマイナスの値!? のケースについては、後述のベルマン-フォード法で扱います。)
[事前補足]
• Startノードからノードn に至る暫定最短距離を distance(n) と表記する。
1. 以下の初期化を行う。
1-1. Startノードs に対して distance(s) = 0 を設定。
1-2. Startノード以外の全ノードn に対して、 distance(n) を ∞ (無限大)に初期化。
( ※ 最初、Startノードから各ノードへの最短距離は不明なため、∞で初期化 )
1-3. 距離未確定ノード集合U に全ノードを追加する。
2. 距離未確定ノード集合Uが空でない限り、以下の探索処理をループ。
2-1. 距離未確定ノード集合U から distance(u) が最小となるノードu を取り除く。
このとき、ノードu のdistance(u) を実際の最短距離として確定する。
(※ 初回のノードu としてStartノードが該当する。distance = 0 で最小となるため。)
(1) ノードu がGoalノード場合:
探索終了して3. へ
2-2. ノードu に隣接している全てのノードv に対して、以下を実施。
(1) distance(v) > distance(u) + uv間のエッジの長さ となる場合:
• distance(v) ← distance(u) + uv間のエッジの長さ に更新
• ノードv の"経路元ノード"として、ノードu を設定
3. Goalノードから順々に経路元ノードを辿る経路(終着はStartノード)を
最短経路として出力。
流れを簡単に説明します。探索のメイン処理は上記 2. のループ処理です。2. のループ処理は次のような動きになります。2-1. でそのループ時点で距離未確定ノード集合U のうち暫定最短距離 distance(u) が最小となるノードu を取り出します。特に初回ループは、distance=0となるStartノードがノードu に該当します。この時点でノードu の暫定最短距離を実際のノードu の最短距離として確定させます。そして、2-2. でそのノードu と隣接しているノードv に対して、ノードuを介してノードvに到達する距離がこれまで記録されているノードvの暫定最短距離より短かければノードvの暫定最短距離を更新し、経路元ノードにノードu を設定します。
この 2. の処理ループを回していくと、ループ毎に最短距離が確定したノードu が1つ決まり、一方で距離未確定ノード集合U に残っているノードは1つ減っていきます。 また、2-2. でノードv の暫定最短距離も随時更新されていきます。このループ処理の過程で、2-1. のノードu としてGoalノードが取り出されたら、その時点でGoalノードの最短距離が確定します。あとはGoalノードから経路元ノードを辿れば、それが最短経路になるという流れです。
アルゴリズムの過程で不思議に思うところとして、2. のループ中に 2-1. で取り出されたノードu の暫定最短距離を実際のノードu の最短距離として確定するところです。初回ループや2巡目であれば、Startノード自身やStartノードと直接隣接しているノードがノードu に該当するので自明ですが、実はループが任意のN巡目であっても、このタイミングで取り出されたノードu は実際の最短距離として確定できることが数学的帰納法で証明されているようです。
まとめると、Startノードの近傍から探索を開始して、その時点での暫定最短距離が最小となっているノードの距離を確定させ、そこから隣接しているノードづてに探索エリアを徐々に広げて行きます。その探索の過程で、Goalノードが引っかかればGoalノードまでの距離と経路を確定します。Startノードの近傍から探索をしていくという点では先ほどの幅優先探索と似ていますが、個々のエッジの長さを加味する点は幅優先探索には無い点です。百聞は一見にしかずということで、こちらもアルゴリズムの動きを見てみましょう。
上のアニメでは、最短距離が確定したノード(アルゴリズム過程の2-1. のノードu )が青色に変わります。ノードの下側に表示される数値が、確定したStartノードからの距離になります。最終的にGoalノードの距離が確定済みになれば最短経路が確定して、最短経路がオレンジ色の線で表示されます。以上がダイクストラ法のアルゴリズムの動きになります。
ダイクストラ法 まとめ
-
最短経路問題で有名なアルゴリズム。
-
個々のエッジの長さが違っていても、非負(0 以上)であれば適用できる。
-
Startノードの近傍のノードから順々に距離を確定して、Goalノードが確定したタイミングで処理終了。
双方向ダイクストラ法
先ほどのダイクストラ法は、Startノードの近傍から順々に各ノードへの距離を確定していき、最終的にGoalノードへの距離を確定するというステップで最短経路を見つけました。逆転の発想で、GoalノードからStartノードへ向けての経路探索も同時に始めてみたらどうなるでしょうか。それが、この節で紹介する双方向ダイクストラ法になります。Startノードからだけ経路探索を始めるのではなく、同時にGoalノードからStartノードへ向けての経路探索も始めて、双方向からの探索が最初に合流した時点で最短経路を確定するというアルゴリズムです。まるでトンネル工事の開通の瞬間みたいなイメージですね。
1. ノード集合S とノード集合G を空にする。
2. 以下の独立した2つの探索処理を並行して始める。
2-A. Startノード起点にダイクストラ法を開始して、
Startノードからの距離が確定したノード(※ 前節ダイクストラ法の 2-1. のノードu)を
集合S に追加する。
2-B. Goalノード起点にダイクストラ法を開始して、
Goalノードからの距離が確定したノード(※ 前節ダイクストラ法の 2-1. のノードu)を
集合G に追加する。
3. 2. での探索中に、ノード集合SとG の両方に含まれるノードm(合流ノード)を検知したら、
2. の探索を終了して4. へ。
4. Startノード → 合流ノードm までの最短経路と、合流ノードm → Goalノードまでの最短経路とを
繋げた経路を最終的な最短経路として出力。
では、双方向ダイクストラ法の動きを見てみましょう。
双方向ダイクストラ法のステップ ( GIFアニメーション )
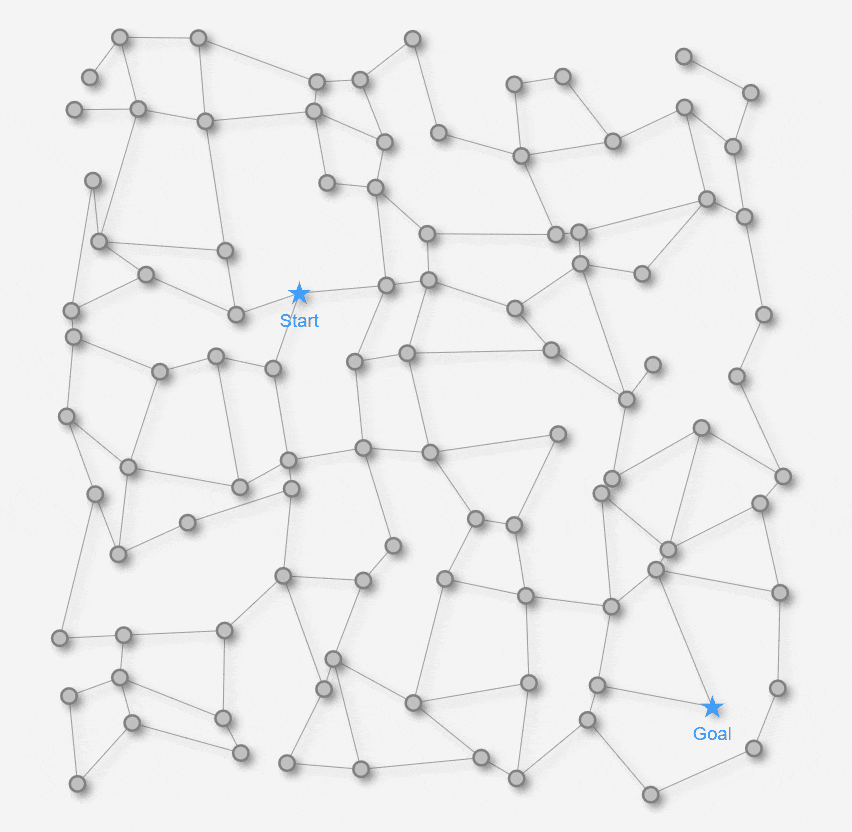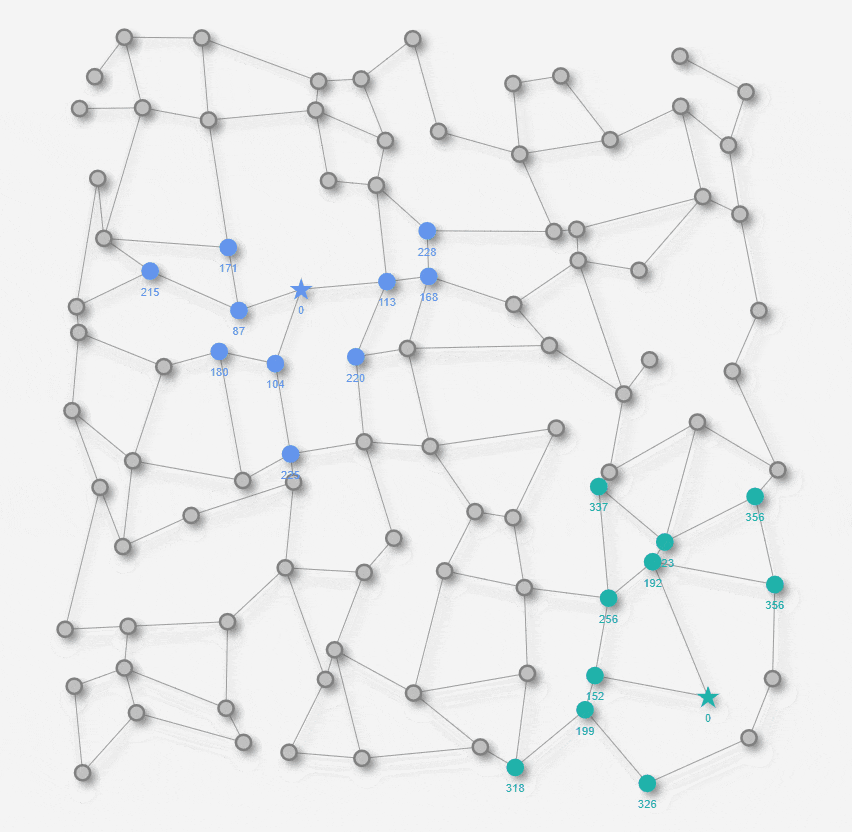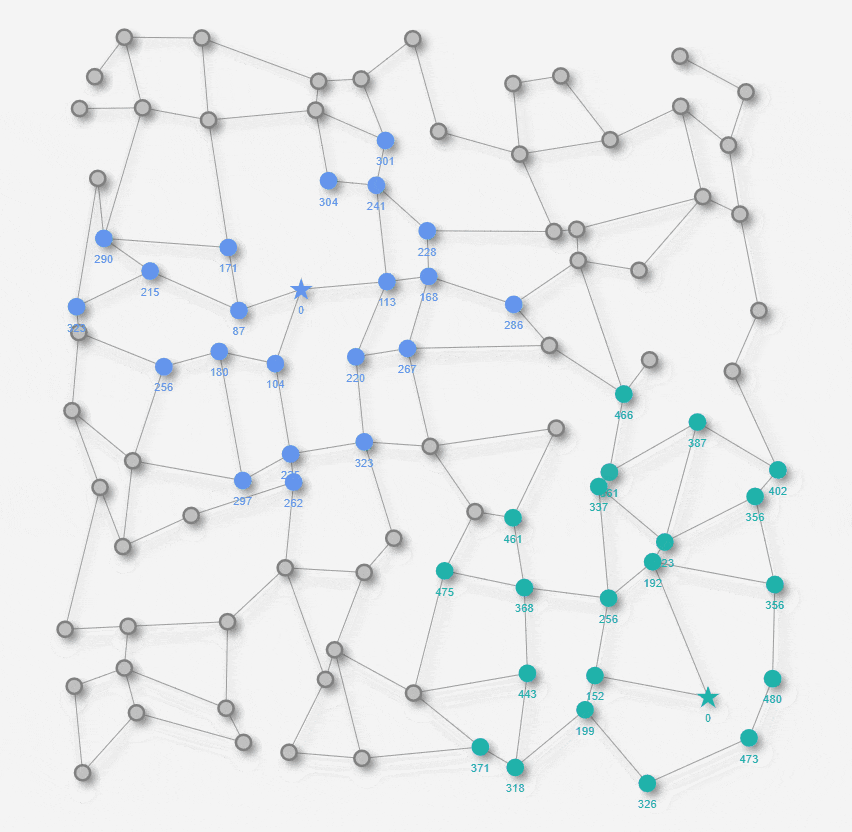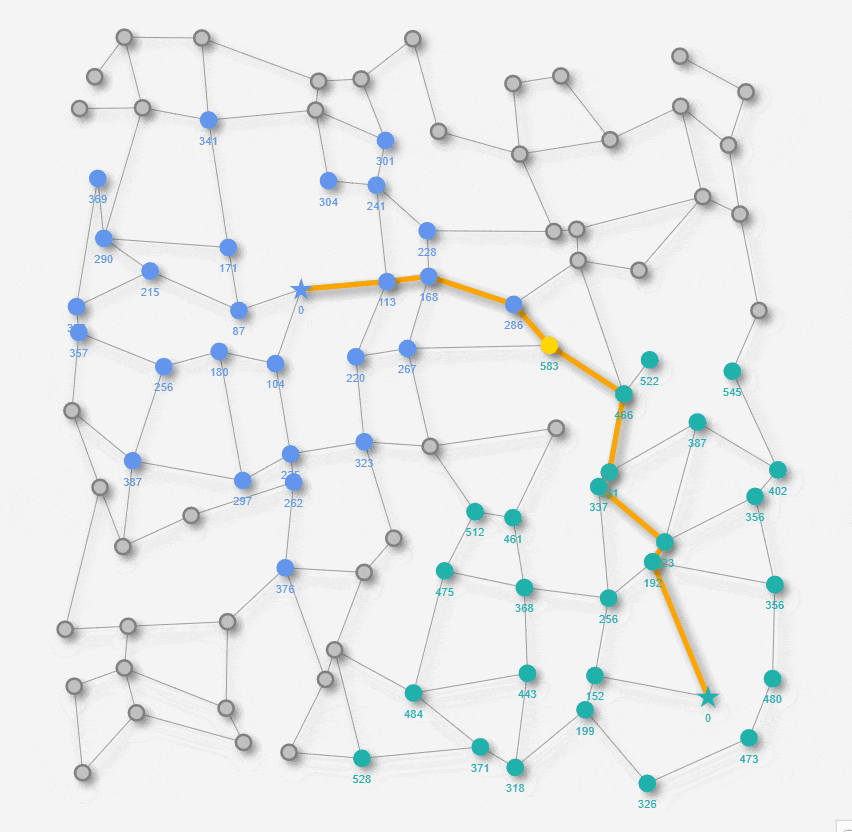
上のアニメでは、Startノード起点のダイクストラ法で 距離が確定したノードが青色に変わります。Goalノード起点のダイクストラ法で 距離が確定したノードが緑色に変わります。青色および緑色ノードの下側に表示される数値は、それぞれStartノード / Goalノードからの確定した距離になります。青色ノード陣営 と 緑色ノード陣営が最初に重なった合流ノードを黄色で表示します。そして最終的に、Startノードから合流ノードの経路と、合流ノードからGoalノードとを繋げた経路が、最短経路としてオレンジ色で表示されます。Startノードからの探索とGoalノードからの探索の双方が接近していくように探索するので、探索の半径が比較的小さいタイミングでも最短経路を見つけることが出来ました。 以上が双方向ダイクストラ法のアルゴリズムの動きになります。
双方向ダイクストラ法 まとめ
-
StartノードとGoalノードの双方向からダイクストラ法を開始して、双方の探索の合流点を見つけ出す。
-
双方向処理のオーバーヘッドはあるが、探索の半径が短くなる分 結果として探索エリアが狭くて済む。
A*(A-start) 法
双方向ダイクストラ法の合流もなかなかドラマチックではありますが、ここでダイクストラ法について、ふと思うことがあります。Startノードから経路探索を開始するとして、明らかにGoalノードと逆方向のノードまで探索するのって無駄じゃない?かと思うわけです。もちろん、それは我々が今この迷路を上から俯瞰できるからそう思えるわけで、現在いるノードとその隣接ノードぐらいしか見えない迷路の真っ只中に居る状況だったら、どの方向への探索が無駄かというのは当然 分かりません。
では、仮に何らかの形でそちらの方向の探索は無駄だよ というヒント情報(※ ヒューリスティック情報と呼びます)を与えることができれば、優先的に探索すべき経路の方向を絞り込めるのではないかと思えるわけです。例えば、もし 目的地は東の方向にあるというヒント情報があれば、西方向への探索の優先度は落とせるわけです。もし GPSなどで現在地と目的地の緯度・経度が分かれば、目的地に近づいているのか、離れていっているのかが分かるわけです。ダイクストラ法にこういったヒント情報を組み込んだ手法の1つに、A(A-star)法*があります。それでは、アルゴリズムの流れを見ていきましょう。
[事前補足]
・Startノードからノードn に至る暫定最短距離を distance(n) と表記する。
・ノードn とGoalノード間の x, y座標上の直線距離を heuristic(n) と表記する。
1. 以下の初期化を行う。
1-1. Startノードs に対して distance(s) = 0 を設定。
1-2. Startノード以外の全ノードn に対して、 distance(n) を ∞ (無限大)に初期化。
( ※ 最初、Startノードから各ノードへの最短距離は不明なため、∞で初期化 )
1-3. 距離未確定ノード集合U に全ノードを追加する。
2. 距離未確定ノード集合Uが空でない限り、以下の探索処理をループ。
2-1. 距離未確定ノード集合U から distance(u) + heuristic(u) が最小となるノードu を取り除く。
( このとき、ノードu のdistance(u) を実際の最短距離として確定する。)
(1) ノードu がGoalノード場合:
探索終了して3. へ
2-2. ノードu に隣接している全てのノードv に対して、以下を実施。
(1) distance(v) > distance(u) + uv間のエッジの長さ となる場合:
• distance(v) ← distance(u) + uv間のエッジの長さ に更新
• ノードv の"経路元ノード"として、ノードu を設定
3. Goalノードから順々に経路元ノードを辿る経路(終着はStartノード)を
最短経路として出力。
流れを簡単に説明します。全体の流れは、ダイクストラ法と同様ですが、異なる箇所は 2-1. でのノードu を取り出すときの評価方法が異なります。ダイクストラ法では、Startノードからの当該ノードまでの距離 distance(u) のみで評価していましたが、A* 法では distance(u) + heuristic(u) で評価しています。heuristic(u) は ノードu からGoalノードへの直線距離なので、Goalノードから離れているノードの場合はheuristic(u) が大きくなります。結果として 2のループ処理の過程で、2-1. にて取り出さるタイミングが相対的に後になります。逆に、Goalノードに近いノードの場合 heuristic(u) が小さくなり相対的に早いタイミングで取り出されます。これが探索の方向付けとなり、Goalに近づくような形で探索の範囲が広がっていきます。実際に、A*アルゴリズムの動きを見てみましょう。
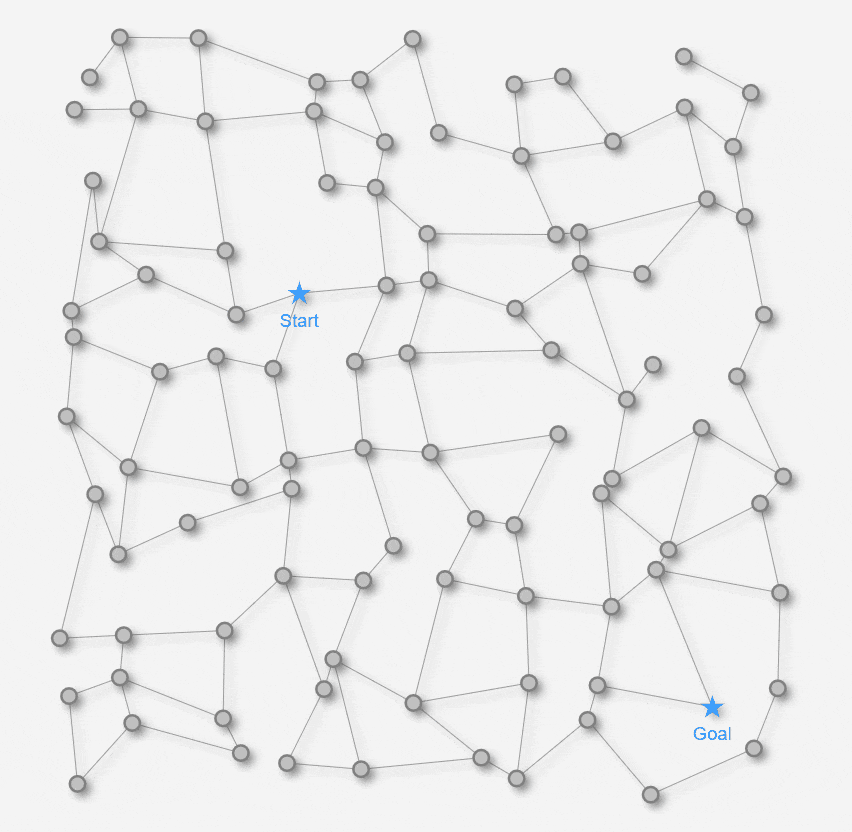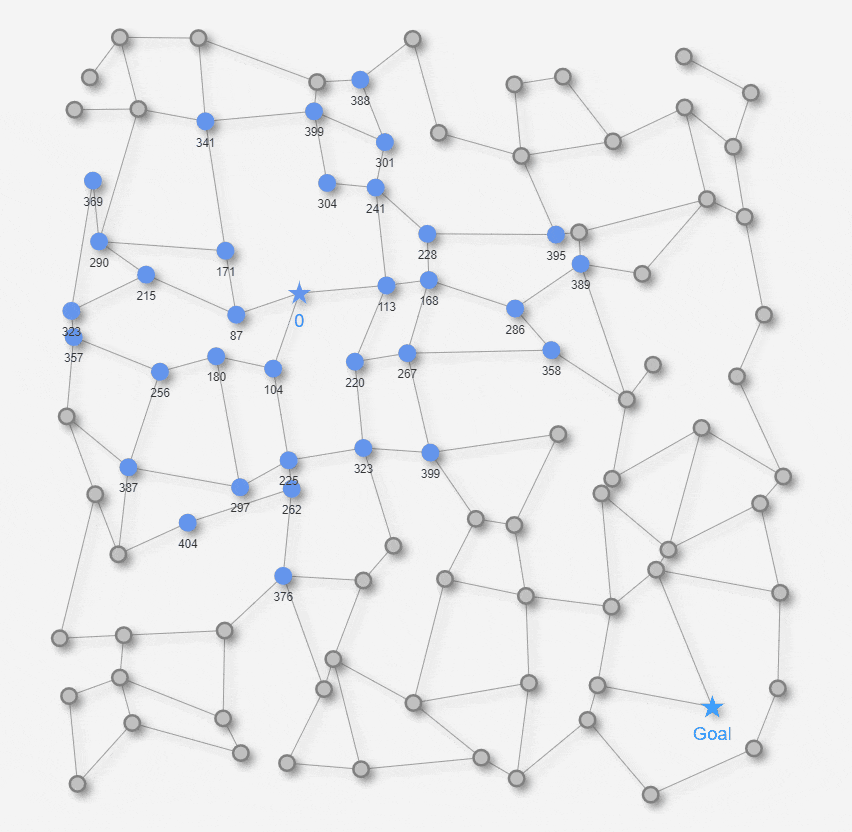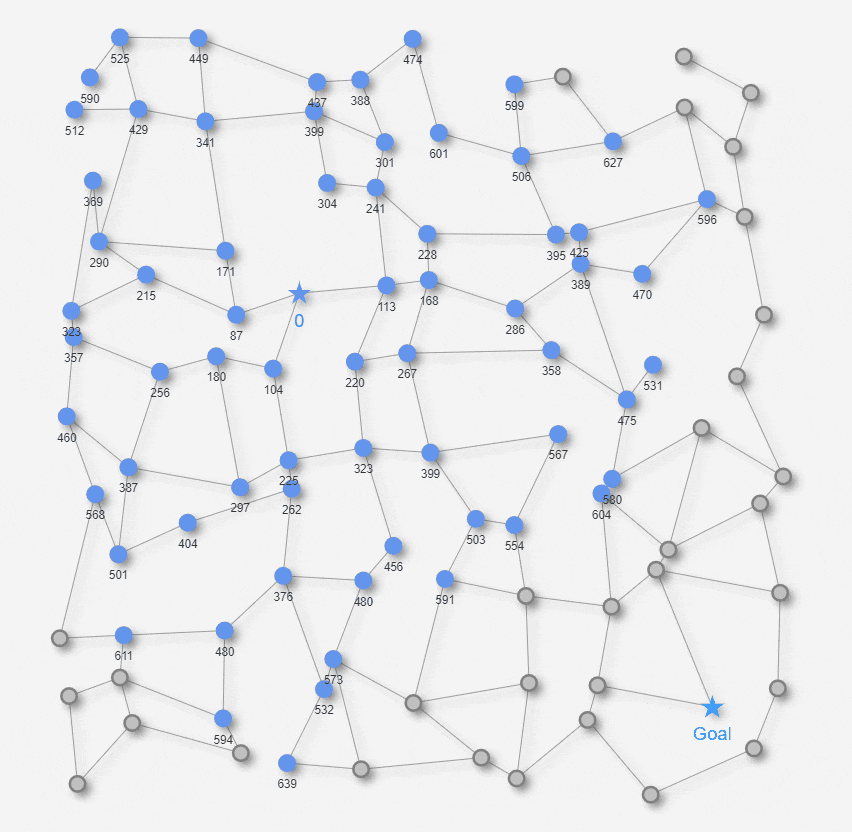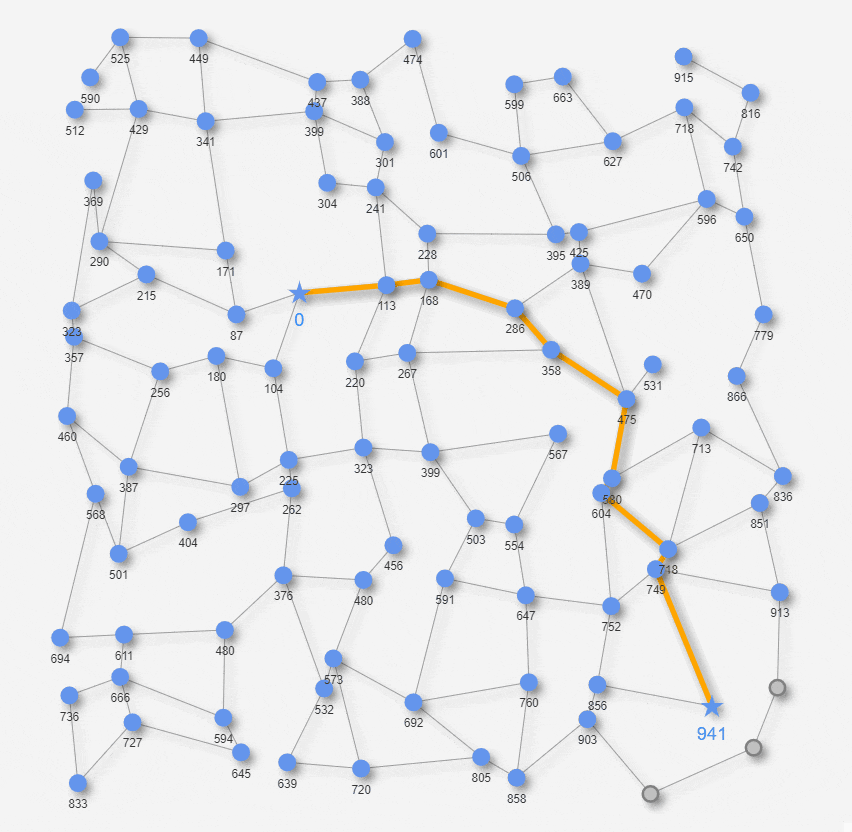
上のアニメもこれまで同様に、距離が確定したノードが青色に変わります。ノードの下側に表示される数値がStartノードからの確定した距離になります。どうでしょうか、Startノードを起点に距離を確定していくステップ自体はダイクストラ法と同じですが、探索する方向付けがダイクストラ法のようにStartノードの近傍から順々に探索するのではなく、Goalノードに近づく方向を優先的に探索しているのが見て取れます。A* 法の場合、Goalに関するヒント情報が与えられているので、そのヒントをもとに早めにGoalノードを探索の網目にかけることが出来ます。逆に言うと、妥当なヒント情報を定義できないケースでは適用が難しく、更にあまりにも実際のコストからかけ離れたヒント情報を与えると正しい解が得られません。今回は平面上の迷路問題なのでヒント情報として直線距離という手頃な定義で済みましたが、妥当なヒント情報を定義できるか否かが一つポイントになります。以上が、A*(A-star)法になります。
A*(A-start) 法 まとめ
-
ダイクストラ法の改良版で、Goalノードに向かって探索エリアを広げて行くので探索が効率的。
-
適切なヒューリスティック情報が定義できれば適用できる。
ベルマン-フォード法
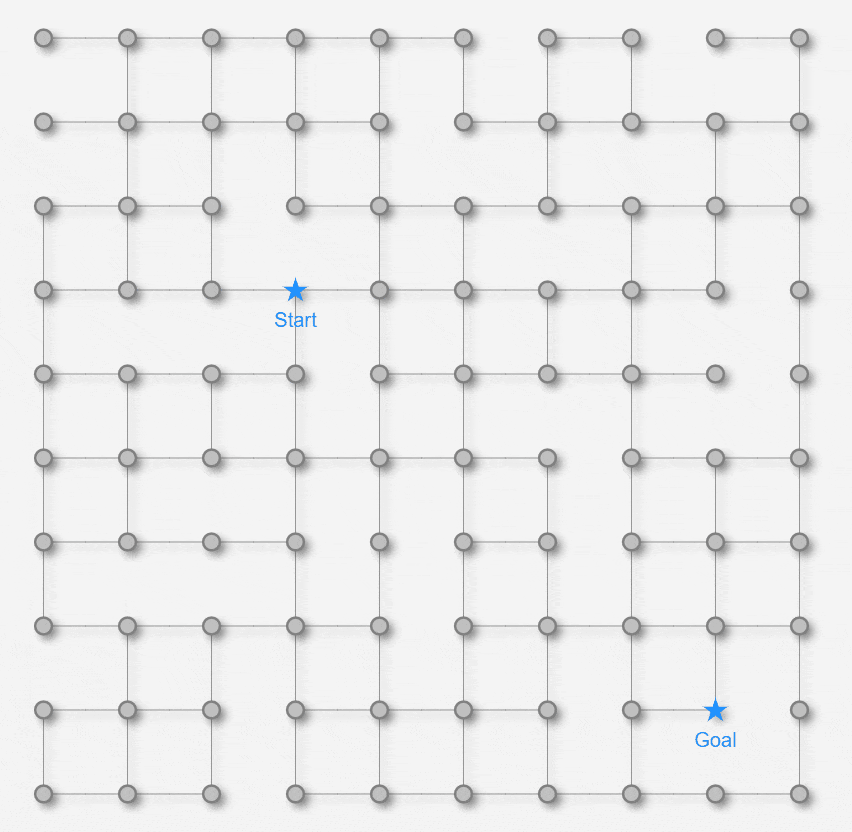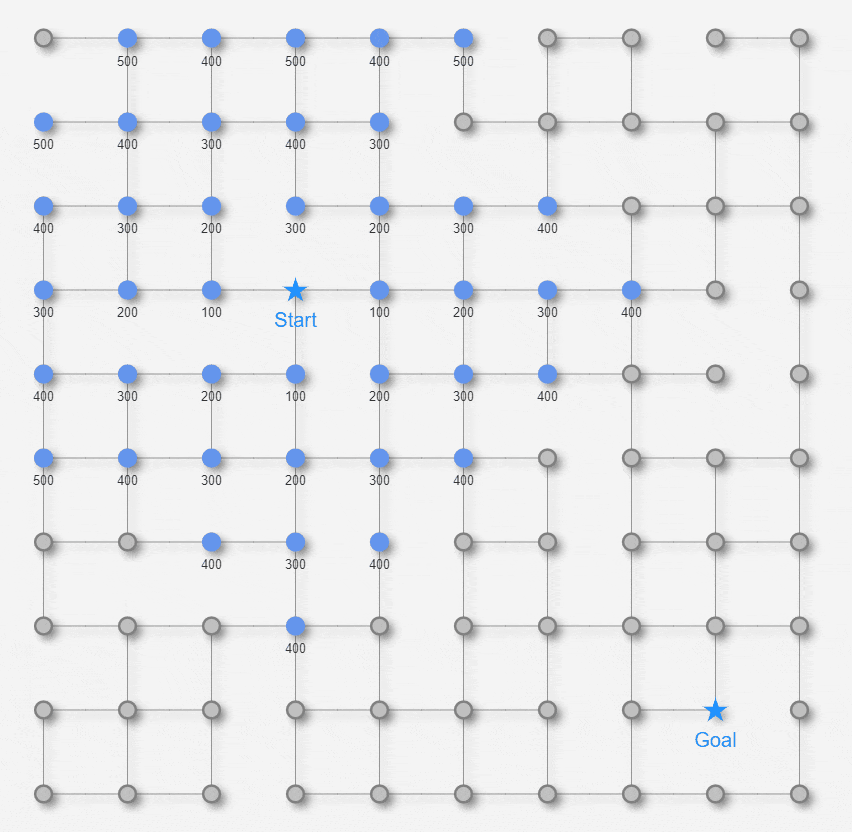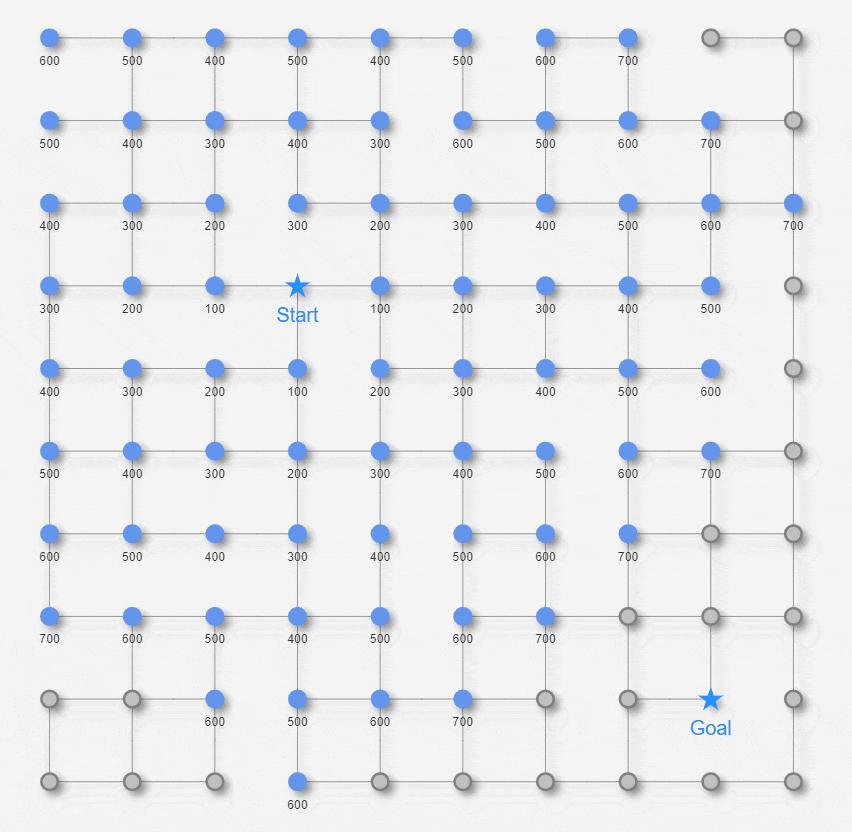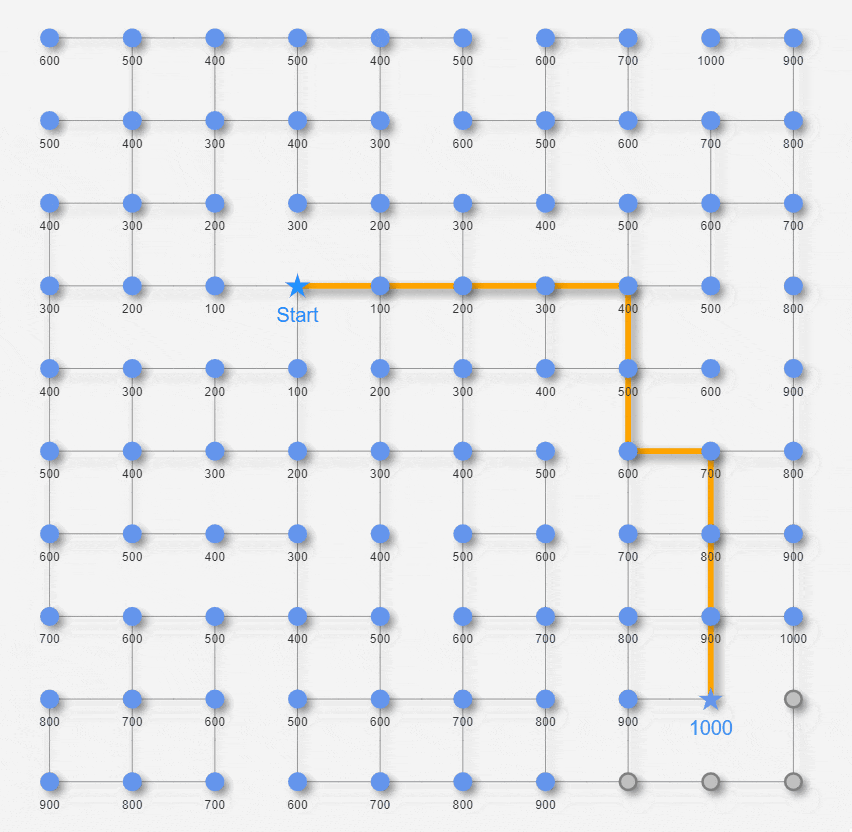
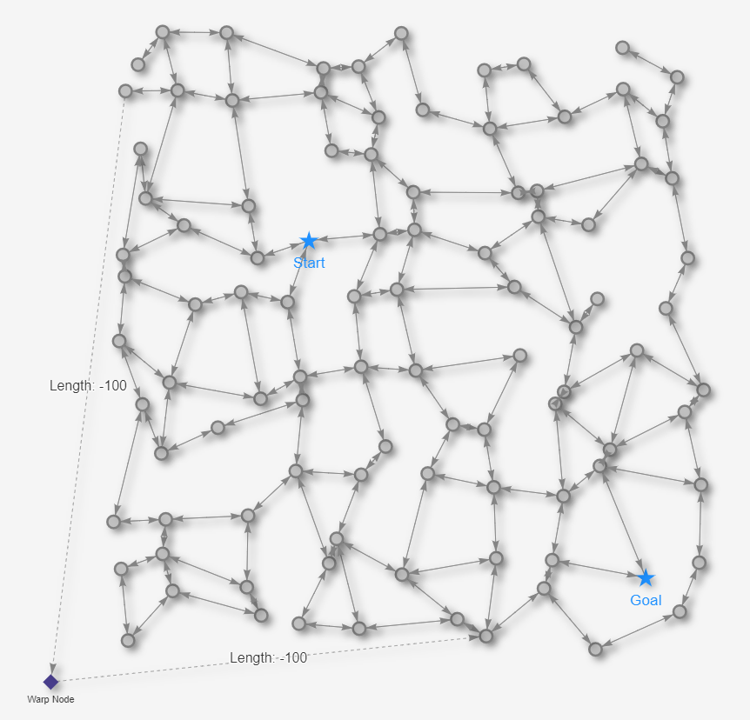
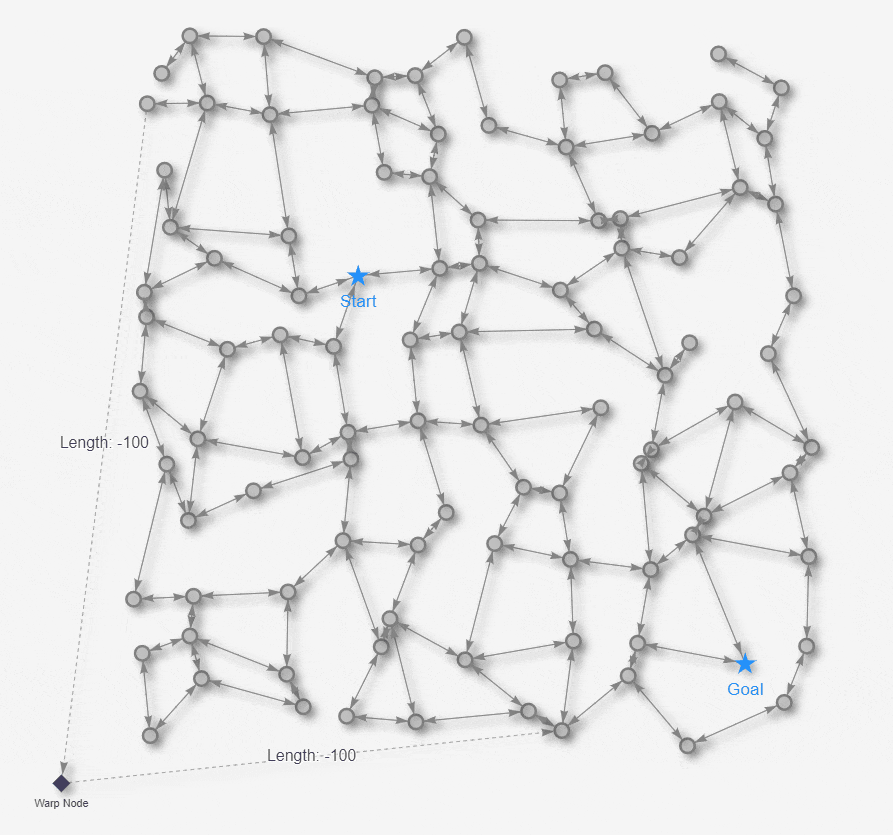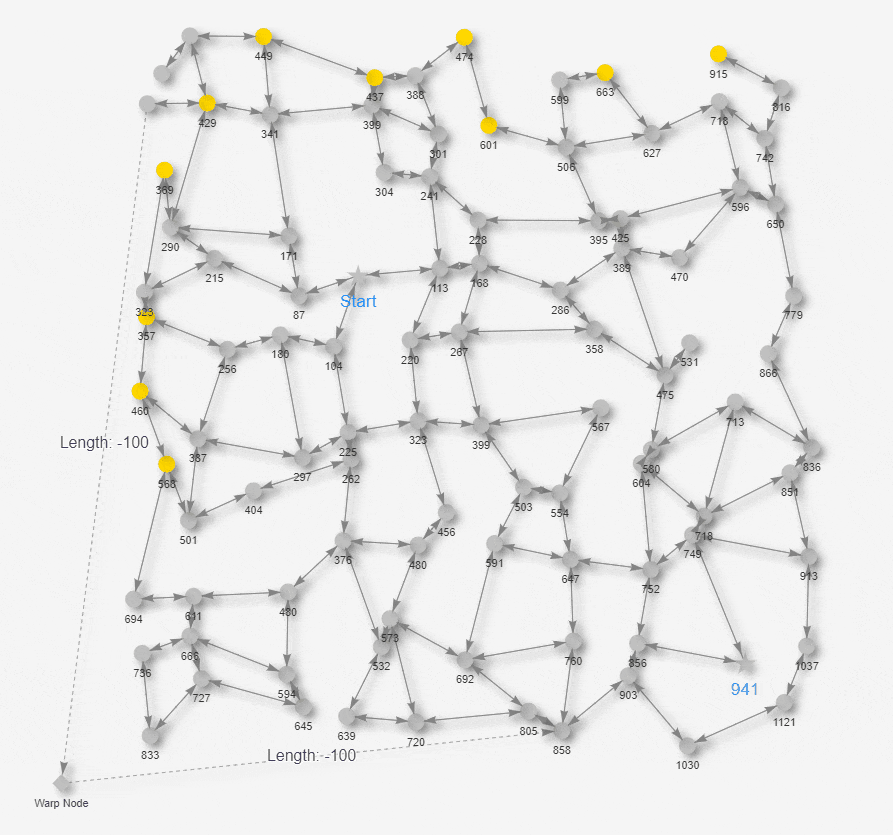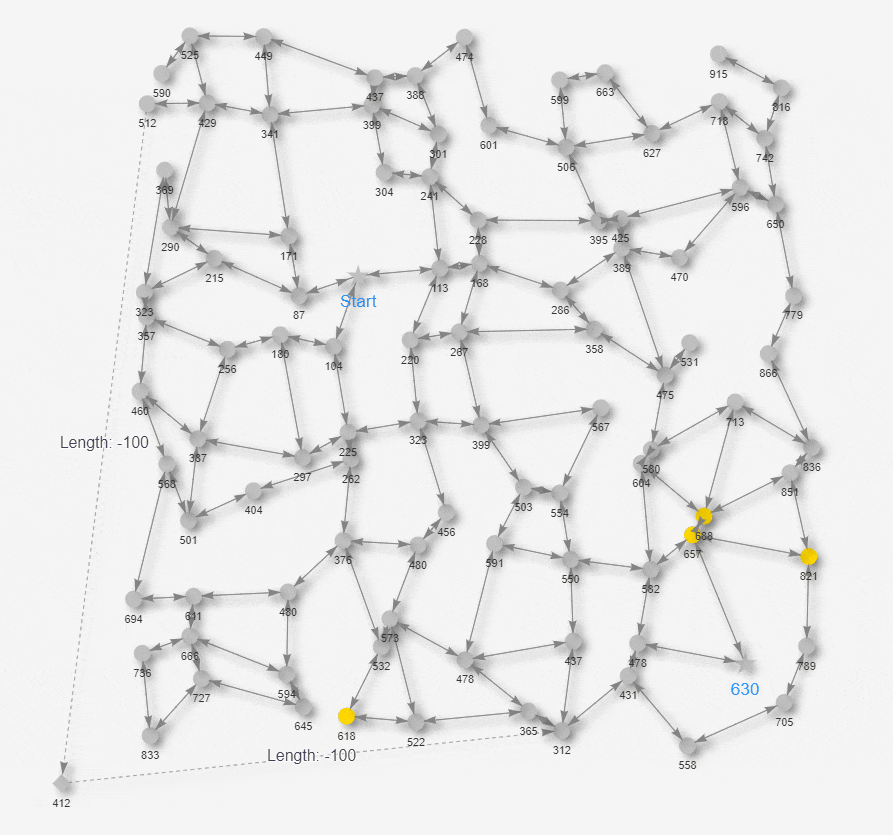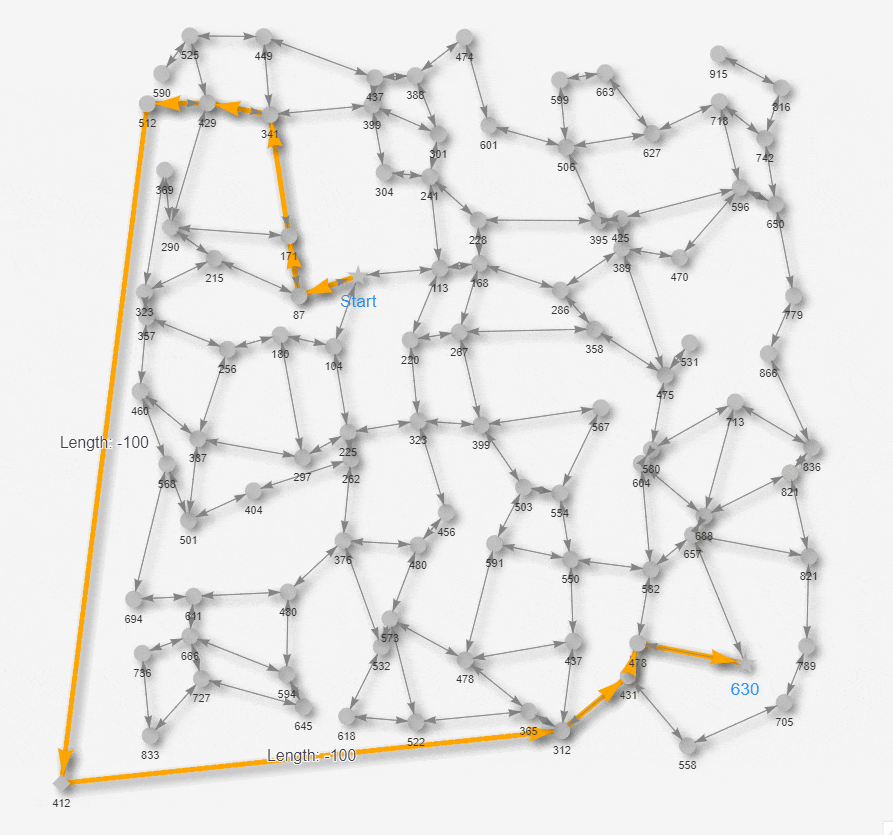
これまで見てきた最短経路アルゴリズムは、エッジの長さが0以上であることを仮定して適用してきましたが、エッジの長さがマイナスの場合でも適用できるアルゴリズムとしてベルマン-フォード法があります。そもそも、エッジの長さがマイナスになるユースケースってどういうケースなの!? か興味深いけど想像も難しいところではありますが…。今回、以下の図のように今までの迷路に架空のワープノード(菱形)を左下に加えて、更にこのワープノードをつたうエッジの長さをマイナス100 としました。つまり このエッジを通過すると、これまでの距離がマイナス100 されるというSF映画さながらの時空の歪みならぬ距離の歪みを発生させるという設定です。
ベルマン-フォード法で、このワープ経路も考慮して最短経路を見つけ出せるのか やってみたいと思います。と、その前にもう1点だけ。今回の迷路については、明示的にエッジの通行の向きを導入します。 エッジの矢印→の向きにしか移動できません。←の矢印と→の矢印の両方があるエッジは相互通行で、片方しか矢印がないエッジは一方通行です。今回 一方通行にしたエッジは、先ほどの長さマイナス100のエッジのみです。仮に これらのエッジを相互通行にすると、この両端ノードを永遠と行ったり来たりするだけで経路の長さがひたすら小さくなって解が求まらなくなるためです。このように、迷路内にグルグル回るといくらでも距離の和がマイナスになるような経路(経路長が負の閉路)が存在する場合は適用できません。
それでは、ベルマン-フォード法でこのワープ経路も考慮して最短経路を見つけ出せるのかやってみます。
[事前補足]
• Startノードからノードn に至る暫定最短距離を distance(n) と表記する。
1. 以下の初期化を行う。
1-1. Startノードs に対して distance(s) = 0 を設定。
1-2. Startノード以外の全ノードn に対して、 distance(n) を ∞ (無限大)に初期化。
( ※ 最初、Startノードから各ノードへの最短距離は不明なため、∞で初期化 )。
2. 以下の探索処理を N回 ループ。 (※ ここで、Nの値は迷路内の全ノードの個数。)
2-1. 迷路の内の全てのノードu に対して、以下を実施。
(1) ノードu → ノードv の向きで隣接している全てのノードv に対して、以下を実施。
distance(v) > distance(u) + uv間のエッジの長さ となる場合:
• distance(v) ← distance(u) + uv間のエッジの長さ に更新
• ノードv の"経路元ノード"を、ノードu に更新
2-2. 上記 2-1. の実行結果にもとづき、以下を実施。
A. 更新が収束した場合(= 全てのノードu において、distance(v) の更新が一度も発生しなかった):
distance(v) の更新が収束したので 3. へ
B. 更新が収束していない場合:
B-1. 現在の2. のループ回数が N-1回目以下なら、2. のループ処理を継続。
B-2. 現在の2. のループ回数が N回目なら、経路長がマイナスの閉路が存在。(異常終了)
3. Goalノードから順々に経路元ノードを辿る経路(終着はStartノード)を
最短経路として出力。
ベルマン-フォード法のステップ ( GIFアニメーション )
上のアニメで黄色になっているノードは、アルゴリズムの過程で暫定最短距離の更新が走っているノードです。ベルマン-フォード法の場合、ダイクストラ法のようにGoalノードが取り出された時点で探索を即打ち切らず、ノード全体の暫定最短距離の更新が収束するまで待つ必要があります。距離の更新が発生しなくなったタイミング、すなわち 黄色のノードが無くなったタイミングで最短経路が確定します。最終結果を見ると、これまでの正規のユークリッド距離より、ワープノード経由で短くなった距離がGoalノードの下に出力されています。以上がベルマン-フォード法を利用して、長さマイナスのエッジを含んだ最短経路探索の動きになります。
ベルマン-フォード法 まとめ
-
ダイクストラ法と違い、長さがマイナスのエッジが存在しても最短経路を見つけ出す。
(※ 但し、経路長がマイナスになる閉路が存在する場合は解が求まらない。) -
ダイクストラ法と違い、全てのノードの最短距離の更新が収束するまでは処理を打ち切れない。
Ant Colony 最適化
最後にご紹介するのはAnt Colony 最適化です。ここまでのアルゴリズムは、決定論的なアプローチで1ノードづつ距離を確定していきました。ここで紹介するアントコロニー最適化はそれとは趣が異なり、ある確率に基づきランダムウォークを繰り返していき、確率論的なアプローチでもって近似的な最短経路を求めていきます。このアルゴリズムのモデルとなっているのが、その名称からもお察しのとおり蟻(Ant)の採餌行動です。
蟻は巣から出て、餌を見つけるとその餌を巣へと持ち帰り、その帰巣の過程でフェロモンを地面に残します。他の蟻達はフェロモンのある経路を優先的に探索して、同様に餌を見つけるとフェロモンを地面に残して帰巣します。加えて このフェロモンは揮発性のため、時間のかかる長い経路の場合はフェロモンが揮発してしまい地面に残りにくく、短い経路の方が地面にフェロモンが残りやすくなります。結果として、より短い経路を中心に蟻が集まり、その経路が強化されていくというモデルです。これを最短経路のアルゴリズムとして昇華したのがAnt Colony最適化アルゴリズムです。詳しく知りたい方は、当記事の導入で紹介した「進化計算アルゴリズム入門 生物の行動科学から導く最適解」を参考になさって下さい。
Ant Colony 最適化は、あくまでフェロモン量に応じた確率的な経路選択シミュレーションなので、上記のやり方で必ず最短経路が見つかることが保証されているわけではありません。また、シミュレーションのやり方にも自由度があると思います。細部は省いていますが、今回 自分が取り組んでみたシミュレーションの流れを次に記します。
1. 以下の初期化を行う。
1-1. 現在までに見つかった暫定最短経路のエッジ順列S を空にする。
1-2. 全エッジに対して、フェロモン値の初期値(0より大きい値)を設定する。
2. Ant N 匹を以下のルールで、一定時間(または一定回数)の間
独立してランダムウォークさせ続ける。
また、単位ステップ毎に全エッジ上のフェロモン値を、揮発率 v(1未満)で減衰させる。
Antのルール:
A. Startノードからランダムウォークを開始する。
• 探索開始にあたって、エッジの訪問順列P を空にする。
B. 今いるノードから隣接しているノードに、次の要領で移動する。
確率ε で (1) ランダム選択 を実施し、 確率 1-ε で (2) フェロモン量に応じた選択 を実施。
(※ ε-greedy 法。通常、ε には小さい確率を設定。)
(1) ランダム選択: (色々な道を試してみる選択)
隣接しているエッジ達から一様ランダムに1つエッジを選択。
選択したエッジの反対側ノードへ移動。
エッジの訪問順列P に選択したエッジを追加。
(2) フェロモン量に応じた選択: (フェロモンの道しるべを活用する選択)
隣接しているエッジ達に付与されているエッジ量に正比例する確率で隣接エッジを1つ選択。
選択したエッジの反対側ノードへ移動。
エッジの訪問順列P に選択したエッジを追加。
C. Goalノードに到達した場合、以下の処理を行う。
C-1. エッジの訪問順列P の経路の長さ に反比例する量のフェロモンを
訪問順列P 内のエッジ上のフェロモン値に加算する。
C-2. エッジの訪問順列P の経路の長さ < 暫定最短経路のエッジ順列S の経路の長さ の場合:
暫定最短経路のエッジ順列S ← Antのエッジの訪問順列 P に更新
C-3. A. から繰り返す。
3. 2. での一定時間(または一定回数)が終了したら、暫定最短経路のエッジ順列S を
最短経路として出力する。
それでは、Ant Colony 最適化の動きを見てみましょう。これまでと同じ迷路に蟻を30匹ほどランダムウォークさせてみます。
Ant Colony 最適化のステップ ( GIFアニメーション )
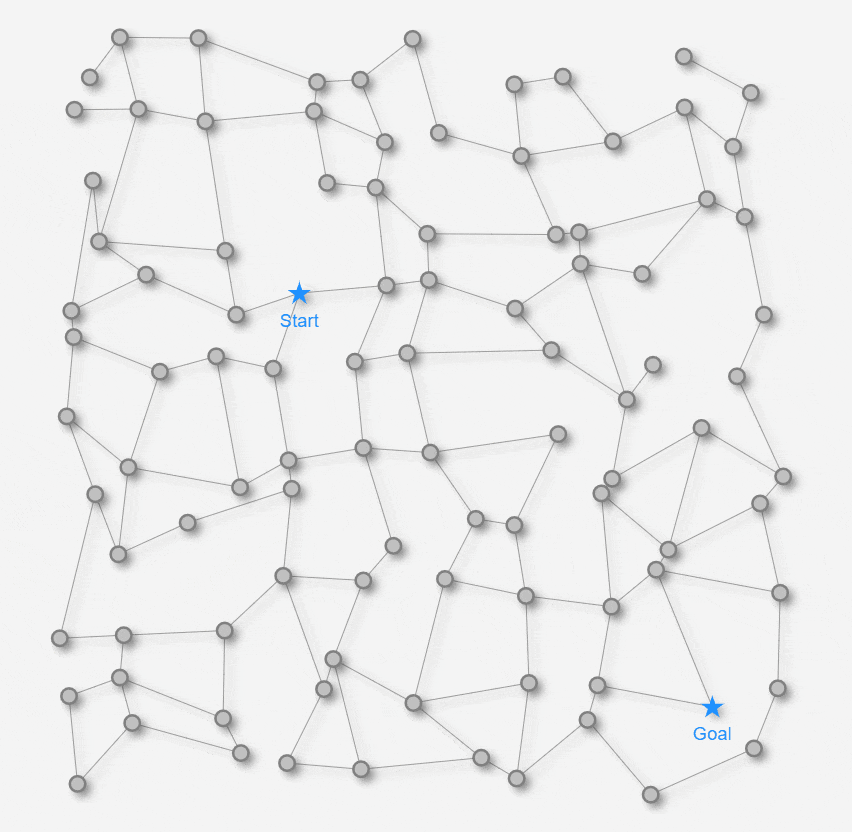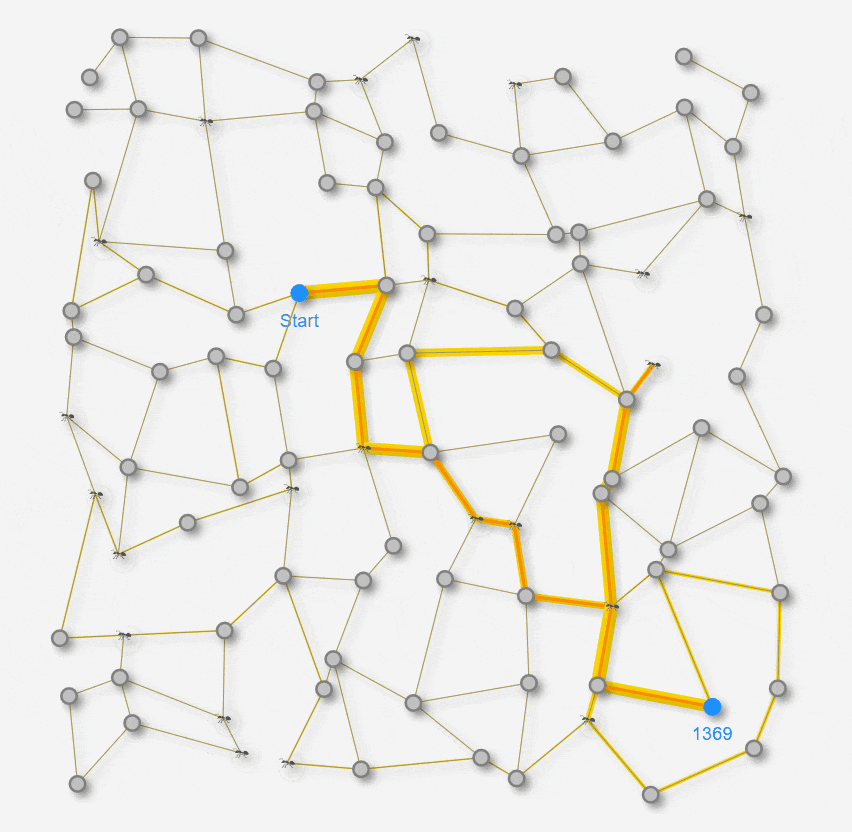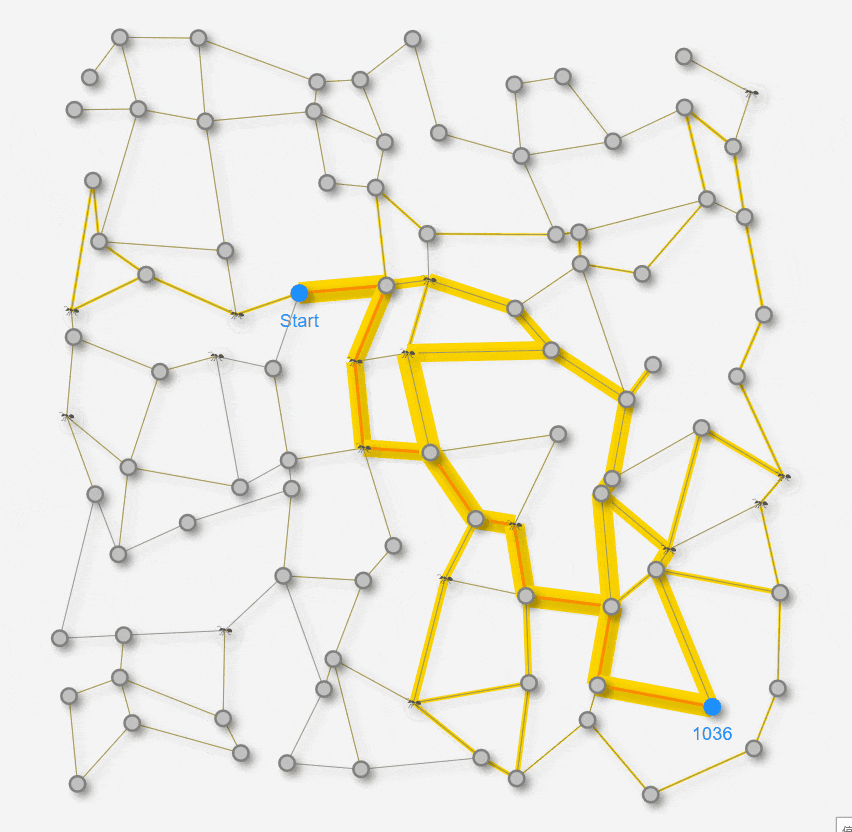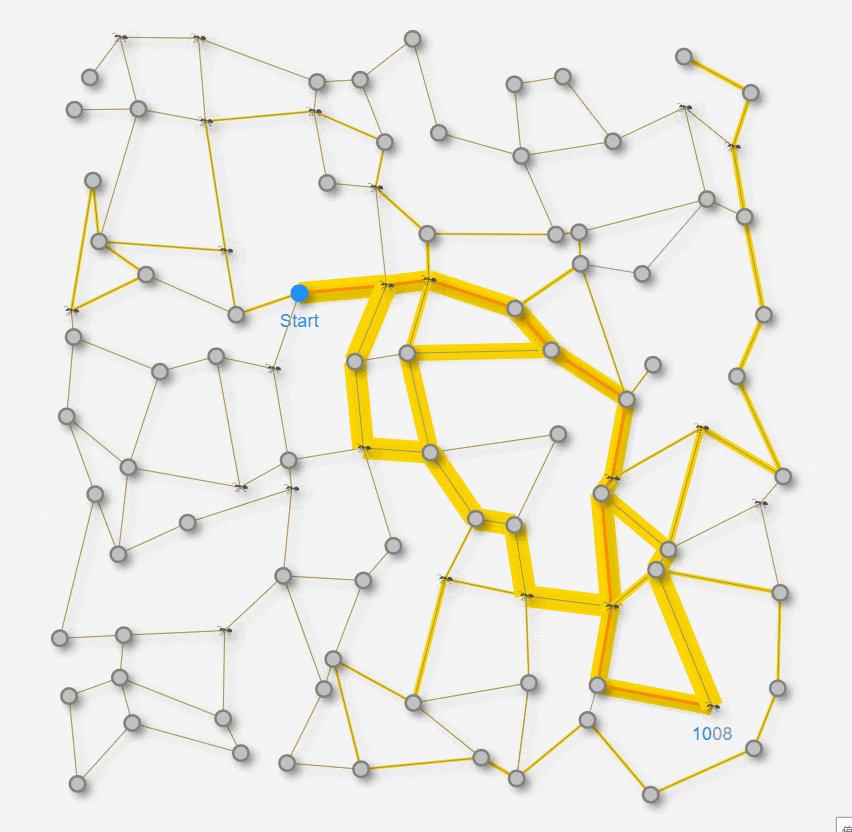
上のアニメでは蟻が移動したノードに蟻のアイコンが表示されます。蟻が迷路上を探索している様子が見てとれると思います。エッジの周りの黄色の背景がフェロモン量を表しています。黄色の背景が太いほど、現在 多くのフェロモンが残っていることを示しています。ステップの経過とともに揮発率に応じてフェロモン量が減衰していきます。もちろん、蟻達が再度 そのエッジを辿ってGoalすると再度 フェロモンを加増します。こうやって、フェロモンの揮発と加増が繰り返されていきます。オレンジ線は、これまでに蟻が見つけた暫定 最短経路を表示しています。新しくもっと短い経路が見つかれば、オレンジの経路は更新されます。以上を一定時間 シミュレーションした模様が上記のアニメーションになります。
最短経路を見つけるというのは、人類だけでなく昆虫にとっても重要な関心事ということを認識しました。蟻さん、賢い!
Ant Colony 最適化 まとめ
-
蟻の採餌行動をもとにした、ランダムウォークベースの経路探索。
-
より短い経路上のエッジが確率的に選択されやすくするアプローチ。
まとめ
当記事では以下の 2点間(単一始点-単一終点)の最短経路アルゴリズムについて、そのステップが目で追えるように可視化にフォーカスして紹介してきました。一方で、各アルゴリズムの計算量については詳しく触れられてませんので、冒頭の参考資料等にあたっていただければと存じます。
- 幅優先探索
- ダイクストラ法
- 双方向ダイクストラ法
- A* 法
- ベルマン-フォード法
- Ant Colony 最適化
Start地点からGoal地点への最短経路を見つけるというシンプルな目的ながら、各アルゴリズムの探索方法の特徴であったり、適用可能・不可能なケースなど様々あるなと改めて感じました。また、今回 視覚化やイメージのし易さを念頭に「迷路」を題材に選びましたが、「辺の長さ(距離としてのコスト)」を時間やお金のコストと捉え直すと、最短経路問題は 最速経路問題 や 最安経路問題 としても捉えることが出来ます。電車乗換えなどがよい例で、最速経路や最安経路など検索してくれますよね。普段 何気なく目にしているモノ(駅や線路など)でもノードやエッジとして見立てると、色々と面白い発見があるかもしれません。
記事は以上になります。ありがとうございました。
また、記事内のアルゴリズムに対する誤認識などありましたらご指摘下さい。