どうも、こんにちは森の生活者のガマ仙人です。
単振動の微分方程式
$$\frac{d^{2}}{d t^{2}} x{\left (t \right )} = - ω^{2} x{\left (t \right )}$$
をsympyで解くと次のようになります。
from sympy import *
init_printing(use_latex=True)
x = Symbol('x') #振動の位置
w = Symbol('ω') #角速度
t = Symbol('t') #時間
# 単振動の微分方程式を定義する
eq = Eq(x(t).diff(t,2), -w**2*x(t))
# 微分方程式を解いてみよう
ans =dsolve(eq,x(t))
# 結果を表示してみる
display(ans)
{x{\left (t \right )} = C_{1} e^{- i t ω} + C_{2} e^{i t ω}}
これだと慣れている人にはいいのですが
ワシのような一般人にはちょっと目に痛いです。
sin(t)とcos(t)が入り混じった式のほうが親近感がありますよね。
そこで
これを置き換えてみようと思ったのでした。
で、オイラーの公式
e^{i x}=cos{x}+isin(x)
を使って置き換えのため.replaceメソッドでいろいろやってはみたのですが
eix=lambda t: (cos(t) + i*sin(t))
ans.replace(exp(i*x),eix)
こういう書き方はできないようっすね
絶望的な気分でリファレンスを読んでいたらいいのを見つけました。
.rewariteメソッドです。
これを使うとexp->sinとか
またその逆とかいろいろできそうなんです。
ans.rewrite(sin)
ってやると、あら不思議。
こんな感じで変換されるのね。
ちょっと感動してしまった。
x{\left (t \right )} = C_{1} \left(- i \sin{\left (t ω \right )} + \cos{\left (t ω \right )}\right) + C_{2} \left(i \sin{\left (t ω \right )} + \cos{\left (t ω \right )}\right)
というわけで、とりあえずはこれでOKなんだけどね
せっかくだからもう少しシンプルにしたいですよね。
そこで積分定数C1,C2を複素共役でくくってやればよいわけですよね。
C1=(a+ib)/2
C2=(a-ib)/2
これを式に代入してやると次のような結果になります。
a,b,C1,C2 = symbols(['a','b','C1','C2'])
ans3 =ans2.subs([(C1,(a+I*b)/2),(C2,(a-I*b)/2)])
ans3
x{\left (t \right )} = \left(\frac{a}{2} - \frac{i b}{2}\right) \left(i \sin{\left (t ω \right )} + \cos{\left (t ω \right )}\right) + \left(\frac{a}{2} + \frac{i b}{2}\right) \left(- i \sin{\left (t ω \right )} + \cos{\left (t ω \right )}\right)
でこれをsimplifyで簡略化しますと
ans4=simplify(ans3)
ans4
x{\left (t \right )} = a \cos{\left (t ω \right )} + b \sin{\left (t ω \right )}
となるわけです。
いわいる普通の振動の式になりましたね。
めでたしです。
いやあ、ここまでくるのに結構時間がかかりました。
おまけですが
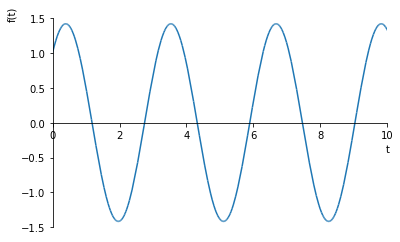
結果をグラフにしてみましょう。
ω=2,a=1.b=1としたグラフです。
plot(ans4.rhs.subs([(w,2),(a,1),(b,1)]),(t,0,10))
ちょっと駆け足で説明してしまいましたが
補足説明が必要な部分もありそうです。
気が付いたら加筆、修正しますね。
以上。