これは【unityプロ技②】 Advent Calendar 2019の18日目の記事です。

こんな感じの「風に揺れる布シェーダー」をUnityで実装したので、簡単に解説します。

頂点シェーダーで揺らめく布を実装しました。
元のMeshは適度に分割したGridで、縦方向に折りたたむことも可能です。
解析的に法線を導出しているので、モバイルでも余裕で動作するくらい負荷が軽量です。#Unity3D #CreativeCoding #Shader #HLSL pic.twitter.com/79XgCc44q6
— がむ (@gam0022) October 30, 2019

軽さの秘訣

このシェーダー、なんとモバイルでも余裕で動作するくらい軽量です！

その軽さの秘訣は、次の3点です！

布の動きを頂点シェーダーで計算
- スキニングの計算やクロスの物理シミュレーションが不要
解析的に法線を導出
- 数値解を求めるよりも計算量を削減
計算をなるべく頂点シェーダーで行う
- （Meshによるが）ピクセル数よりも頂点数の方が少ない
- 頂点シェーダーで動きや法線を計算することで、GPUの計算量を削減

環境

2018.4.13f1 (LTS)
Build-in Rendering Pipeline

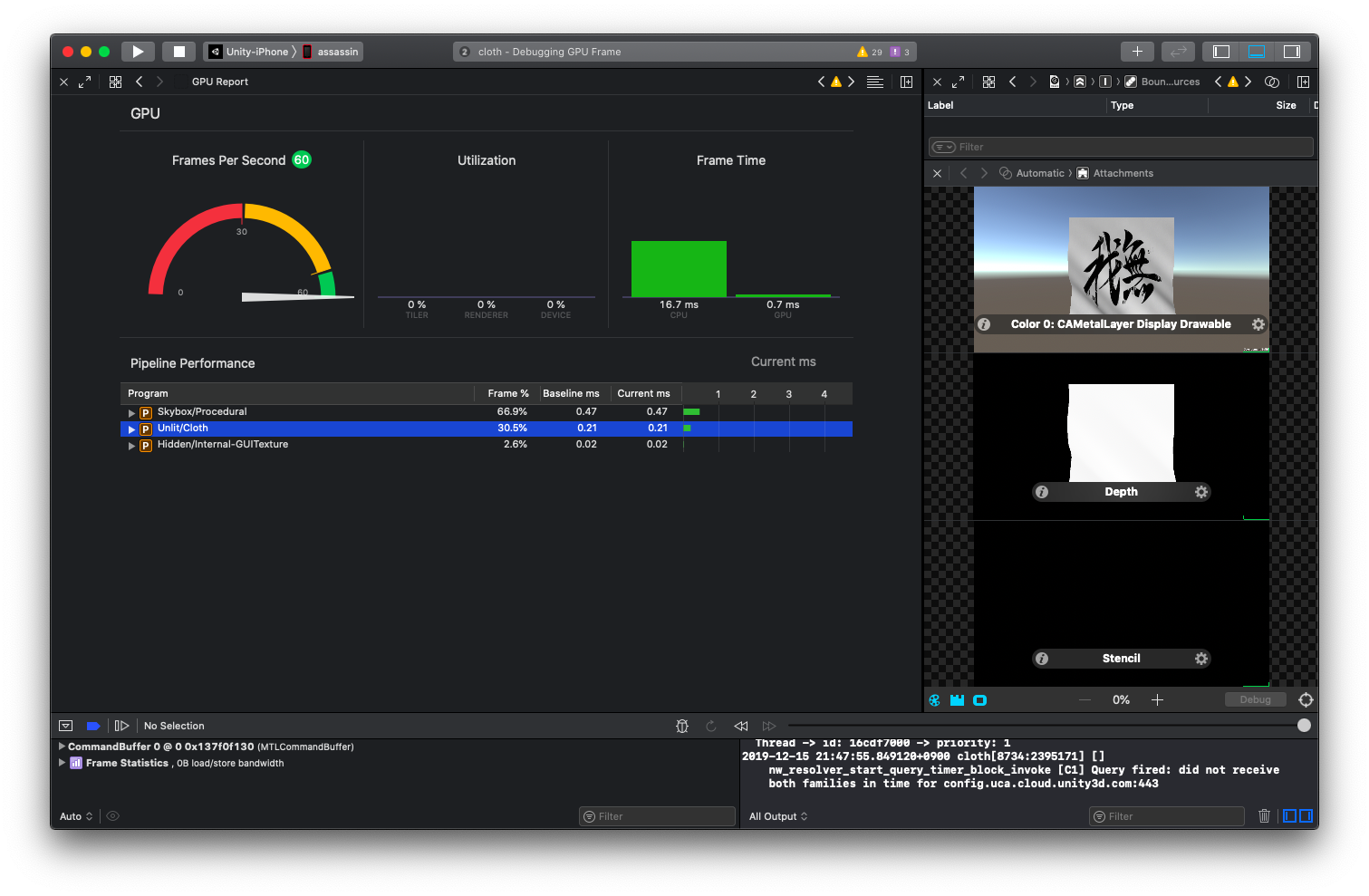
GPU負荷の実機計測

iPhone8 と Xcode11.3 でGPU負荷を計測したところ、布シェーダーの実行時間は 0.21 ms でした。

これはUnity標準のSkyboxの半分以下のGPU負荷です。

また、iPhoneは前のフレームのGPU負荷によってGPU性能が可変のようなので、最大のGPU性能を発揮したときは、さらに実行時間が減ると思われます。

シェーダ全文

シェーダー全文とUnityプロジェクトはGitHubに公開しています。

GitHubおよび本記事に登場するソースコードはMIT Licenseです。

シェーダー解説

実装を踏まえながら、シェーダーを解説していきます。

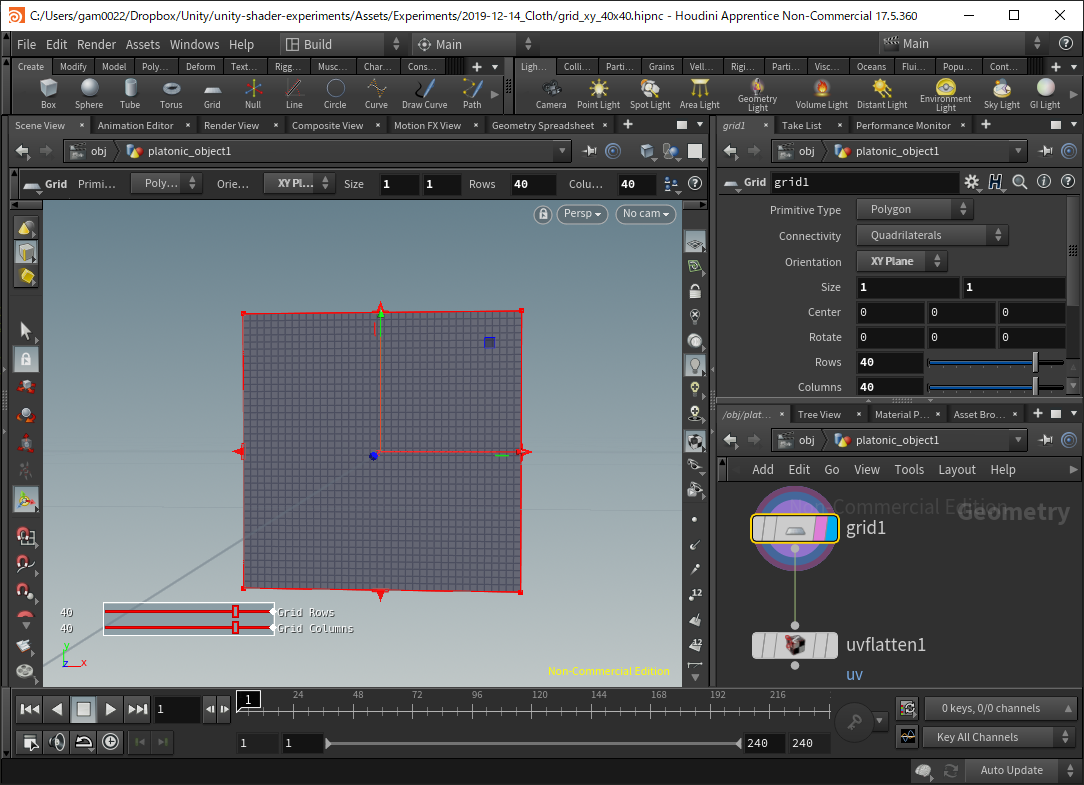
Meshの準備

1x1の大きさのGridをつくります。分割数は 40x40 くらいが丁度いいです。UVも必要です。

Houdiniの場合は、GridノードとUV Flattenノードで作れます。

頂点シェーダーの解説

まず、頂点シェーダーから実装を解説していきます。

頂点シェーダー

v2f vert(appdata v)
{
    v2f o;

    // UVの斜め方向のパラメータを t と定義します
    float t = v.uv.x + v.uv.y;

    // 周波数とスクロール速度から t1 を決定します
    float t1 = _WaveFreq1 * t + _WaveSpeed1 * _TIME;

    // 波の高さ wave1 を計算します
    float wave1 = _WaveAmplitude1 * sin(t1);

    // wave1 を t1 で偏微分した dWave1 を計算します
    float dWave1 = _WaveFreq1 * _WaveAmplitude1 * cos(t1);

    // wave1 と同様にして wave2 を計算します
    float t2 = _WaveFreq2 * t + _WaveSpeed2 * _TIME;
    float wave2 = _WaveAmplitude2 * sin(t2);
    float dWave2 = _WaveFreq2 * _WaveAmplitude2 * cos(t2);

    // 上部を固定するための値を計算します
    float fixTopScale = (1.0f - v.uv.y);

    // 2つの波を合成して、頂点座標に反映します
    float wave = fixTopScale * (wave1 + wave2);
    v.vertex += wave;

    // 波（位置）を偏微分した勾配から、法線を計算します
    float dWave = fixTopScale * (dWave1 + dWave2);
    float3 objNormal = normalize(float3(dWave, dWave, -1.0f));
    o.normal = mul((float3x3)unity_ObjectToWorld, objNormal);

    o.vertex = UnityObjectToClipPos(v.vertex);
    o.uv = TRANSFORM_TEX(v.uv, _MainTex);

    return o;
}

波の動きの計算とMeshの変形

まず最初に波の動きを計算します。

今回は単純に2つの sin 波（wave1 と wave2）の重ね合わせて波を作り出しました。

// 1つ目の波
float t1 = _WaveFreq1 * t + _WaveSpeed1 * _TIME;
float wave1 = _WaveAmplitude1 * sin(t1);

// 2つ目の波
float t2 = _WaveFreq2 * t + _WaveSpeed2 * _TIME;
float wave2 = _WaveAmplitude2 * sin(t2);

// 2つの波を合成して、頂点座標に反映します
float wave = fixTopScale * (wave1 + wave2);
v.vertex += wave;

波が1つだけだと動きが非常に単調になってしまうので、振幅と周波数が違う複数の波を重ねることで、より自然な波の動きにしています。
これは非整数ブラウン運動やfBm と呼ばれる有名なシェーダーのテクニックです。
また、波の振幅と周波数はプロパティ化して、インスペクタで微調整できるようにすると便利です。

最後に、波の高さを頂点座標に加算することで、波の動きに合わせてMeshを変形します。

解析的な法線の導出

いよいよ 最重要ポイントである解析的な法線の導出 の解説です。

一言で説明すると、陰関数を偏微分した勾配から法線を計算しています。

波の関数は z 方向の高さマップなので、次の式で表されますが、

z = f(x, y)

変形によって陰関数となります。

g(x, y, z) = f(x, y) - z = 0

xy平面の斜め方向を t と定義します。
こうすることで、xとyの偏微分の結果が同じになるので、計算量を少しだけ減らせます。

t = x + y\\
g(t, z) = f(t) - z = 0

// UVの斜め方向のパラメータを t と定義します
float t = v.uv.x + v.uv.y;

また、t に周波数と時間によるスピードの影響を加えて、 t1 = _WaveFreq1 * t + _WaveSpeed1 * _TIME と定義します。

// 周波数とスクロール速度から t1 を決定します
float t1 = _WaveFreq1 * t + _WaveSpeed1 * _TIME;

ここで、

a = _WaveFreq1
b = _WaveAmplitude1
c = _WaveSpeed1 * _TIME
- tに依存しない定数とみなせるので、まとめて変数にします

と変数をおくと、

wave1 = _WaveAmplitude1 * sin(_WaveFreq1 * t + _WaveSpeed1 * _TIME)

は

wave1 = b * sin(a * t + c)

となるので、wave1 を t で偏微分します。

\frac{\partial}{\partial t} g(t,z ) = \frac{\partial}{\partial t} (b \sin(a t + c) - z) = \frac{\partial}{\partial t} b \sin(a t + c) = a b \cos(a t + c)

以上により、 wave1 を偏微分した dWave1 の解析解が求まり、HLSLで実装すると以下のようになります。

位置を偏微分

// 波の高さ wave1 を計算します
float wave1 = _WaveAmplitude1 *  sin(t1);

// wave1 を t1 で偏微分した dWave1 を計算します
float dWave1 = _WaveFreq1 * _WaveAmplitude1 * cos(t1);

dWave2 も同様に計算ができて、wave1 と wave2 はそれぞれ独立しているので、それぞれ微分してから足し合わせても同じ結果になります。

また、g を z で偏微分をすると -1 の定数になります。

\frac{\partial}{\partial z} g(t, z) = \frac{\partial}{\partial z} f(t) - z = -1

以上により、法線 $n$（勾配）を計算するための、波の関数の偏微分が求まりました。

n = (\frac{\partial}{\partial t} g(t, z), \frac{\partial}{\partial t} g(t, z), \frac{\partial}{\partial z} g(t, z)) = (a b \cos(a t), a b \cos(a t), -1)

HLSLにすると、こうなります。

// 波（位置）を偏微分した勾配から、法線を計算します
float dWave = fixTopScale * (dWave1 + dWave2);
float3 objNormal = normalize(float3(dWave, dWave, -1.0f));
o.normal = mul((float3x3)unity_ObjectToWorld, objNormal);

フラグメントシェーダーの解説

フラグメントシェーダーでは、頂点シェーダーで求めた法線とDirectionalLightからライティング計算をして、最終的なピクセルの値を決定します。

フラグメントシェーダー

half4 frag(v2f i) : SV_Target
{
    half4 col = tex2D(_MainTex, i.uv);
    col *= _TintColor * _LightColor0;

    // DirectionalLight によってライティングします
    half diffuse = saturate(dot(i.normal, _WorldSpaceLightPos0.xyz));

    // 影の強さを _ShadowIntensity で調整します
    // _ShadowIntensity = 0.5 で Half-Lambert と同じ効果が得られます
    half halfLambert = lerp(1.0, diffuse, _ShadowIntensity);
    col.rgb *= halfLambert;

    return col;
}

カスタムシェーダーからDirectionalLightを利用

DirectionalLightのパラメータは次のから取得できます。

ワールド空間の方向：_WorldSpaceLightPos0.xyz から
ライトのカラー：_LightColor0

これらのパラメータをシェーダーから参照するためには、Tagsに "LightMode" = "ForwardBase" を指定する必要がありました。

Tagsに"LightMode"を指定

    Tags{
        "Queue" = "Geometry"
        "RenderType" = "Opaque"
+       "LightMode" = "ForwardBase"
        "IgnoreProjector" = "True"
    }

少し一般化した Half-Lambert

ライティングには少し一般化した Half-Lambertを用いました。

まずは法線とライトの内積から完全拡散反射を計算します。

half diffuse = saturate(dot(i.normal, _WorldSpaceLightPos0.xyz));

このままだと、陰影がハッキリしすぎて不自然なので、 _ShadowIntensity というパラメータで陰影の強さを調整できるようにしました。

_ShadowIntensity = 0.5 で Half-Lambert の計算式と同値になります。

half halfLaumber = lerp(1.0, diffuse, _ShadowIntensity);

簡易なライティングですが、計算量と品質のバランスは取れており、モバイルなら必要十分だと思います。

さらに軽量化が必要な場合は、このライティング処理を頂点シェーダーで行うという方法もありますが、シェーダーの見通しの良さを重視して、今回はピクセルシェーダーで実装しました。

おわりに

いかがでしたでしょうか？

「短いシェーダーと簡単な数式だけでも、ちゃんと揺れる布を実装できるんだ！」
というのが伝われば幸いです。

レイマーチングでも、 陰関数を偏微分した勾配から法線を導出 するテクニックが有名ですが、それと同じ理論で法線を導出しています。

レイマーチングでは、距離関数を数値的に偏微分する必要があるため、距離関数を複数回（4～6回）評価する必要がありますが、
今回は波の式を単純化することによって、解析的に偏微分を行って計算量を減らしました。

数学の知識を応用すると、シェーダーをシンプルかつ軽量に実装ができます！

数学をつかって複雑な課題をシンプルに解決できたときの快感が、私は好きです。

[Unity] モバイルでも動く！風に揺れる布シェーダー（解析的な法線導出）