LoginSignup
68
60

More than 5 years have passed since last update.

Three.jsAdvent Calendar 2016Day 8
@gam0022(Sho Hosoda)inKLab 株式会社

three.jsの組み込みuniform/attributeの紹介

Last updated at Posted at 2016-12-08

この記事は、Three.js Advent Calendar 2016 8日目の記事です。

はじめに

みなさんはthree.jsのカスタムシェーダを使った経験はありますか？

three.jsでは、THREE.ShaderMaterialからカスタムシェーダを利用できます。具体的にはTHREE.ShaderMaterialのコンストラクタで頂点シェーダとフラグメントシェーダを指定してMaterialを生成できます。

THREE.ShaderMaterialと似たようなクラスにTHREE.RawShaderMaterialがあります。
THREE.ShaderMaterialではビルドインのuniform/attributeの定義がシェーダの先頭に挿入されますが、THREE.RawShaderMaterialでは挿入されないという違いがあります。

three.jsでカスタムシェーダをバリバリ使いこなす人は、意図しないコードが挿入されるのを避ける目的でTHREE.RawShaderMaterialを使うケースが多いかもしれませんね！

ちなみにTHREE.ShaderMaterialでも組み込みのuniform/attributeが定義されていないだけなので、定義を自分で宣言することで使用できます。例えば、THREE.RawShaderMaterialのフラグメントシェーダにuniform vec3 cameraPosition;と宣言すれば、実際にカメラのグローバル座標を受け取ることができます。

THREE.RawShaderMaterialしか使わないにせよ、three.jsにどのような組み込みuniform/attributeが存在するのかを把握することは、three.jsを理解する上では有用だと考えます。

そこで、この記事ではthree.jsの組み込みのuniform/attributeを紹介します。

なお、three.jsのバージョンは執筆時点の最新のr82になります。

three.js r82の組み込みuniform/attribute

以下がthree.js r82の組み込みuniform/attributeです！ バーン！（効果音）

three.js r82の組み込みuniform/attribute - gist

長すぎて見辛いので、本文ではなく外部のgistのリンクの形にさせていただきました。

「えっ…？長すぎでは？（困惑）」と思った方もいるでしょう。THREE.ShaderMaterialを使うと、何もしなくてもこんな大量のコードが埋め込まれます。ビックリしちゃいますよね。

ちなみに、WebGL InspectorというGoogle Chrome拡張をインストールして、実際にWebGLに渡されたシェーダのコードを調査しました。

three.jsの組み込みuniform/attributeの解説

いきなり長いGLSLのコードを貼り付けて申し訳ございません。
ここからはthree.jsの組み込みuniform/attributeの解説をしていきます。

精度(precision)について

まずは先頭から見ていきましょう。
頂点シェーダもフラグメントシェーダも精度は highp です。

precision highp float;
precision highp int;

モデルやカメラの行列

WebGLの座標系について

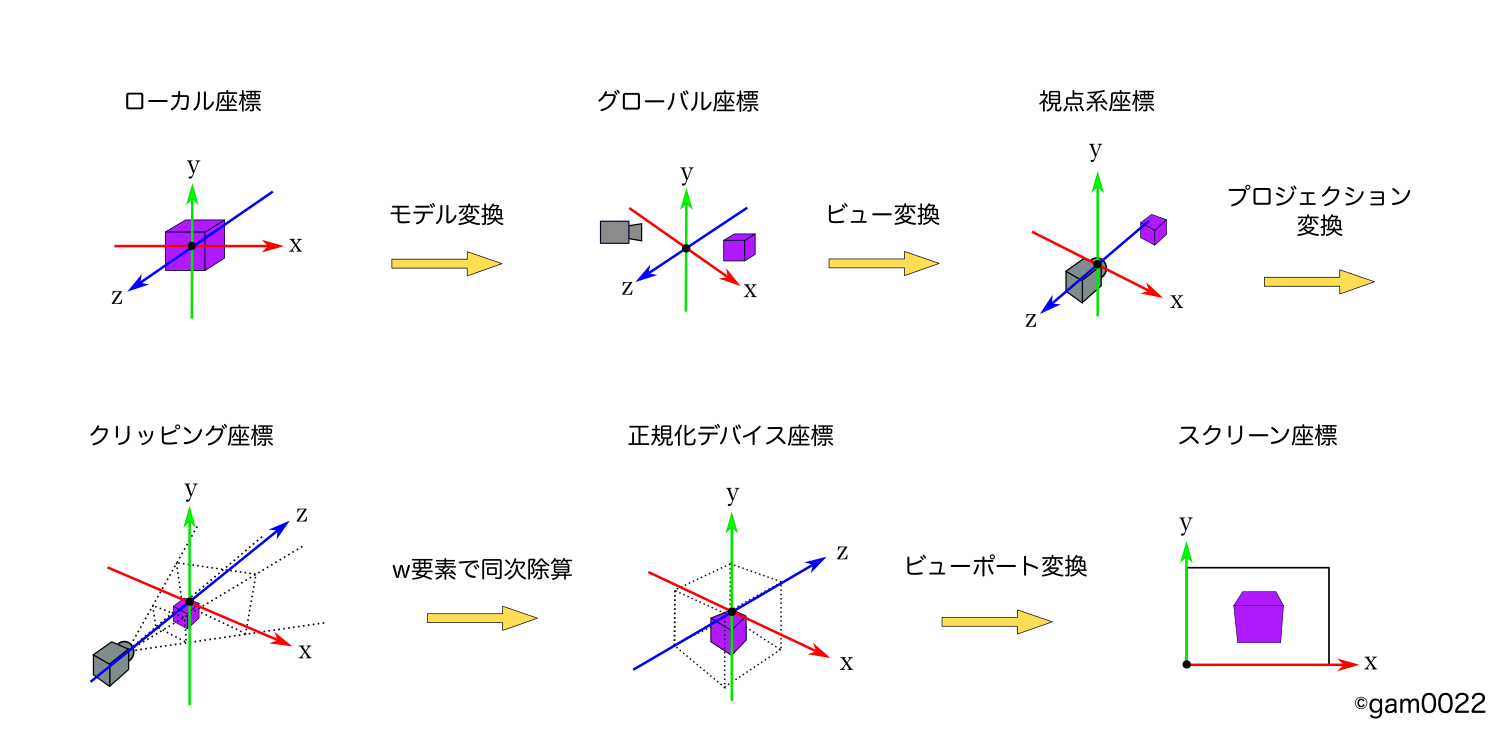
モデルやカメラの行列の紹介の前に、図をつかって軽くWebGLの座標系について整理します。

coordinate_system.png

（この図はInskscapeを使って頑張って描きました。）

WebGLを含む3DCGのAPIの描画の裏側では、ローカル座標からスタートし、スクリーン座標がゴールとなる頂点の座標の変換が行われています。

まずは6つ座標系を知っておきましょう。

ローカル座標
モデリングソフトが出力したオブジェクトそのままの頂点の座標です。
つまり物体の原点からみたポリゴンの頂点の座標がローカル座標です

グローバル座標（別名ワールド空間）
オブジェクトを平行移動や回転や拡大縮小すると、頂点の座標も連動して変化します。
シーンの中心を原点とみなした座標がワールド座標です

視点系座標（別名ビュー空間）
カメラの位置を向きを原点とみなした座標が視点系座標です

クリッピング座標
カメラの視野の範囲であるピラミッド形の空間をクリッピング空間と呼びます（視錐台と呼ぶこともあります）。
このクリッピング空間の中心とした座標系がクリッピング座標です。
頂点シェーダで gl_Position に書き込む座標がクリッピング座標となります

正規化デバイス座標
クリッピング座標を-1.0〜1.0に収まるように正規化した座標です。
このときに-1.0〜1.0に収まらない座標は描画されません

スクリーン座標（別名ウィンドウ座標）
2次元のスクリーン上の座標系です。これがディスプレイ上で目に見える座標になります。
フラグメントシェーダで gl_FragCoord として参照できる座標がスクリーン座標となります。

組み込みで定義される、モデルやカメラの行列

以下は頂点シェーダで実際に定義されるモデルやカメラの行列です。
コメント内に詳しい解説を追記しました。

// 頂点シェーダで定義されるモデルやカメラの行列
uniform mat4 modelMatrix;      // モデル行列。モデルをローカル座標からグローバル座標に変換します。
uniform mat4 modelViewMatrix;  // モデルビュー行列。ローカル座標から視点系座標の変換します。modelViewMatrix = viewMatrix * modelViewMatrix
uniform mat4 projectionMatrix; // カメラのプロジェクション行列。日本語で透視変換行列とも呼びます。視点系座標からクリッピング座標に変換します。
uniform mat4 viewMatrix;       // カメラのビュー行列。カメラのモデル行列の逆行列です。
uniform mat3 normalMatrix;     // ローカル座標の法線を視点系座標に変換する行列です。
uniform vec3 cameraPosition;   // カメラのグローバル座標。

カメラのビュー行列と座標はフラグメントシェーダでも定義されています。

// フラグメントシェーダで定義されるモデルやカメラの行列
uniform mat4 viewMatrix;
uniform vec3 cameraPosition;

頂点情報

頂点情報は以下の4つです。頂点情報なので、頂点シェーダでしか定義されていません。
頂点カラーは#ifdefで囲まれているので、未使用の場合は宣言されません。

// 頂点情報
attribute vec3 position;// 頂点のローカル座標
attribute vec3 normal;  // 頂点のローカル空間での法線の向き
attribute vec2 uv;      // 頂点のUV
#ifdef USE_COLOR
    attribute vec3 color; // 頂点カラー
#endif

色の変換や補正の関数

uniform/attributeに加えて、色を変換や補正のための関数がフラグメントシェーダに定義されています。

トーンマッピング

トーンマッピングは、HDRからLDRへのカラー値のマッピングをする変換のことです。

つまり、8bitを超える範囲の浮動小数点のHDR画像を、通常のカラーディスプレイで表示できる8bitのLDR画像に変換する処理です。

three.jsでは、以下の4種類のトーンマッピングの関数が用意されています。

  • LinearToneMapping(toneMapping)
  • ReinhardToneMapping
  • Uncharted2ToneMapping
  • OptimizedCineonToneMapping

これらのトーンマッピングの実際の動作は公式サンプルから確認できます。

three.jsのデフォルトでUncharted2ToneMappingがあるのは面白いですよね。
PS3の名作ゲーム「Uncharted 2」で実際に使用されているトーンマッピングです。
詳しくはもんしょさんのUncharted 2式Filmicトーンマップに解説があります。

#define TONE_MAPPING
#define saturate(a) clamp( a, 0.0, 1.0 )
uniform float toneMappingExposure;
uniform float toneMappingWhitePoint;
vec3 LinearToneMapping( vec3 color ) {
    return toneMappingExposure * color;
}
vec3 ReinhardToneMapping( vec3 color ) {
    color *= toneMappingExposure;
    return saturate( color / ( vec3( 1.0 ) + color ) );
}
#define Uncharted2Helper( x ) max( ( ( x * ( 0.15 * x + 0.10 * 0.50 ) + 0.20 * 0.02 ) / ( x * ( 0.15 * x + 0.50 ) + 0.20 * 0.30 ) ) - 0.02 / 0.30, vec3( 0.0 ) )
vec3 Uncharted2ToneMapping( vec3 color ) {
    color *= toneMappingExposure;
    return saturate( Uncharted2Helper( color ) / Uncharted2Helper( vec3( toneMappingWhitePoint ) ) );
}
vec3 OptimizedCineonToneMapping( vec3 color ) {
    color *= toneMappingExposure;
    color = max( vec3( 0.0 ), color - 0.004 );
    return pow( ( color * ( 6.2 * color + 0.5 ) ) / ( color * ( 6.2 * color + 1.7 ) + 0.06 ), vec3( 2.2 ) );
}

vec3 toneMapping( vec3 color ) { return LinearToneMapping( color ); }

ガンマ補正

ディスプレイにRGBの強さをそのまま渡すと、RGBの値は線形に出力されずに、中央の値が落ち込んだカーブで出力されて暗めの結果になります。
このディスプレイが実際に出力する色のカーブの形をディスプレイの特性とも呼びます。
ディスプレイのRGBの出力を線形に近づけるために補正が「ガンマ補正」です。

ガンマ補正を自分で実装しても良いですが、LinearToGammaという組み込みの関数も利用できます。

ガンマ補正の他にも、sRGB/RGBE/RGBM/RGBD/LogLuvとRGBを相互に変換する関数まであります。

vec4 LinearToLinear( in vec4 value ) {
    return value;
}
vec4 GammaToLinear( in vec4 value, in float gammaFactor ) {
    return vec4( pow( value.xyz, vec3( gammaFactor ) ), value.w );
}
vec4 LinearToGamma( in vec4 value, in float gammaFactor ) {
    return vec4( pow( value.xyz, vec3( 1.0 / gammaFactor ) ), value.w );
}
vec4 sRGBToLinear( in vec4 value ) {
    return vec4( mix( pow( value.rgb * 0.9478672986 + vec3( 0.0521327014 ), vec3( 2.4 ) ), value.rgb * 0.0773993808, vec3( lessThanEqual( value.rgb, vec3( 0.04045 ) ) ) ), value.w );
}
vec4 LinearTosRGB( in vec4 value ) {
    return vec4( mix( pow( value.rgb, vec3( 0.41666 ) ) * 1.055 - vec3( 0.055 ), value.rgb * 12.92, vec3( lessThanEqual( value.rgb, vec3( 0.0031308 ) ) ) ), value.w );
}
vec4 RGBEToLinear( in vec4 value ) {
    return vec4( value.rgb * exp2( value.a * 255.0 - 128.0 ), 1.0 );
}
vec4 LinearToRGBE( in vec4 value ) {
    float maxComponent = max( max( value.r, value.g ), value.b );
    float fExp = clamp( ceil( log2( maxComponent ) ), -128.0, 127.0 );
    return vec4( value.rgb / exp2( fExp ), ( fExp + 128.0 ) / 255.0 );
}
vec4 RGBMToLinear( in vec4 value, in float maxRange ) {
    return vec4( value.xyz * value.w * maxRange, 1.0 );
}
vec4 LinearToRGBM( in vec4 value, in float maxRange ) {
    float maxRGB = max( value.x, max( value.g, value.b ) );
    float M      = clamp( maxRGB / maxRange, 0.0, 1.0 );
    M            = ceil( M * 255.0 ) / 255.0;
    return vec4( value.rgb / ( M * maxRange ), M );
}
vec4 RGBDToLinear( in vec4 value, in float maxRange ) {
    return vec4( value.rgb * ( ( maxRange / 255.0 ) / value.a ), 1.0 );
}
vec4 LinearToRGBD( in vec4 value, in float maxRange ) {
    float maxRGB = max( value.x, max( value.g, value.b ) );
    float D      = max( maxRange / maxRGB, 1.0 );
    D            = min( floor( D ) / 255.0, 1.0 );
    return vec4( value.rgb * ( D * ( 255.0 / maxRange ) ), D );
}
const mat3 cLogLuvM = mat3( 0.2209, 0.3390, 0.4184, 0.1138, 0.6780, 0.7319, 0.0102, 0.1130, 0.2969 );
vec4 LinearToLogLuv( in vec4 value ) {
    vec3 Xp_Y_XYZp = value.rgb * cLogLuvM;
    Xp_Y_XYZp = max(Xp_Y_XYZp, vec3(1e-6, 1e-6, 1e-6));
    vec4 vResult;
    vResult.xy = Xp_Y_XYZp.xy / Xp_Y_XYZp.z;
    float Le = 2.0 * log2(Xp_Y_XYZp.y) + 127.0;
    vResult.w = fract(Le);
    vResult.z = (Le - (floor(vResult.w*255.0))/255.0)/255.0;
    return vResult;
}
const mat3 cLogLuvInverseM = mat3( 6.0014, -2.7008, -1.7996, -1.3320, 3.1029, -5.7721, 0.3008, -1.0882, 5.6268 );
vec4 LogLuvToLinear( in vec4 value ) {
    float Le = value.z * 255.0 + value.w;
    vec3 Xp_Y_XYZp;
    Xp_Y_XYZp.y = exp2((Le - 127.0) / 2.0);
    Xp_Y_XYZp.z = Xp_Y_XYZp.y / value.y;
    Xp_Y_XYZp.x = value.x * Xp_Y_XYZp.z;
    vec3 vRGB = Xp_Y_XYZp.rgb * cLogLuvInverseM;
    return vec4( max(vRGB, 0.0), 1.0 );
}

vec4 mapTexelToLinear( vec4 value ) { return LinearToLinear( value ); }
vec4 envMapTexelToLinear( vec4 value ) { return LinearToLinear( value ); }
vec4 emissiveMapTexelToLinear( vec4 value ) { return LinearToLinear( value ); }
vec4 linearToOutputTexel( vec4 value ) { return LinearToLinear( value ); }

モーフターゲットとスキニング

モーフターゲットとスキニングに用いられる頂点情報も定義されています。
#ifdefで囲まれているので、未使用の場合は宣言されません。

#ifdef USE_MORPHTARGETS
    attribute vec3 morphTarget0;
    attribute vec3 morphTarget1;
    attribute vec3 morphTarget2;
    attribute vec3 morphTarget3;
    #ifdef USE_MORPHNORMALS
        attribute vec3 morphNormal0;
        attribute vec3 morphNormal1;
        attribute vec3 morphNormal2;
        attribute vec3 morphNormal3;
    #else
        attribute vec3 morphTarget4;
        attribute vec3 morphTarget5;
        attribute vec3 morphTarget6;
        attribute vec3 morphTarget7;
    #endif
#endif
#ifdef USE_SKINNING
    attribute vec4 skinIndex;
    attribute vec4 skinWeight;
#endif

最後に

軽めの記事にするつもりだったのに、組み込みuniform/attributeの紹介だけで、けっこうな文量になってしまいました…汗

カメラやモデルの行列などはシェーダを書くときに意識すると思いますが、それ以外は知らない人も多かったのではないでしょうか？

three.jsを普通に使っていても、組み込みのuniform/attributeに触れる機会は稀だと思います。
もしも、この記事を読んで意外な発見がありましたら、嬉しいかぎりです。

それでは、three.jsで楽しいシェーダライフを送りましょう！

68
60
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
68
60