dFdxとdFdyとは
GLSLにはdFdx/dFfyというフラグメントシェーダで使える組み込み関数があります。
dFdx/dFfyによって、X方向・Y方向の偏微分が計算できます。
偏微分というと、難しそうな印象を受けるかもしれませんが、単なるスクリーン上のピクセル単位の画素値(本当は任意の値)の差分です。
そもそもdFdx/dFfyとは?という方は、先にコチラをご覧になることをお勧めします。
レイマーチングの法線の計算をdFdxとdFdyで行う
dFdxとdFdyによって、スクリーン上での微分から法線を求めることができます。
これで法線が求まるのは単純に面白いですね。同じことをしてる人は見たことがないです。
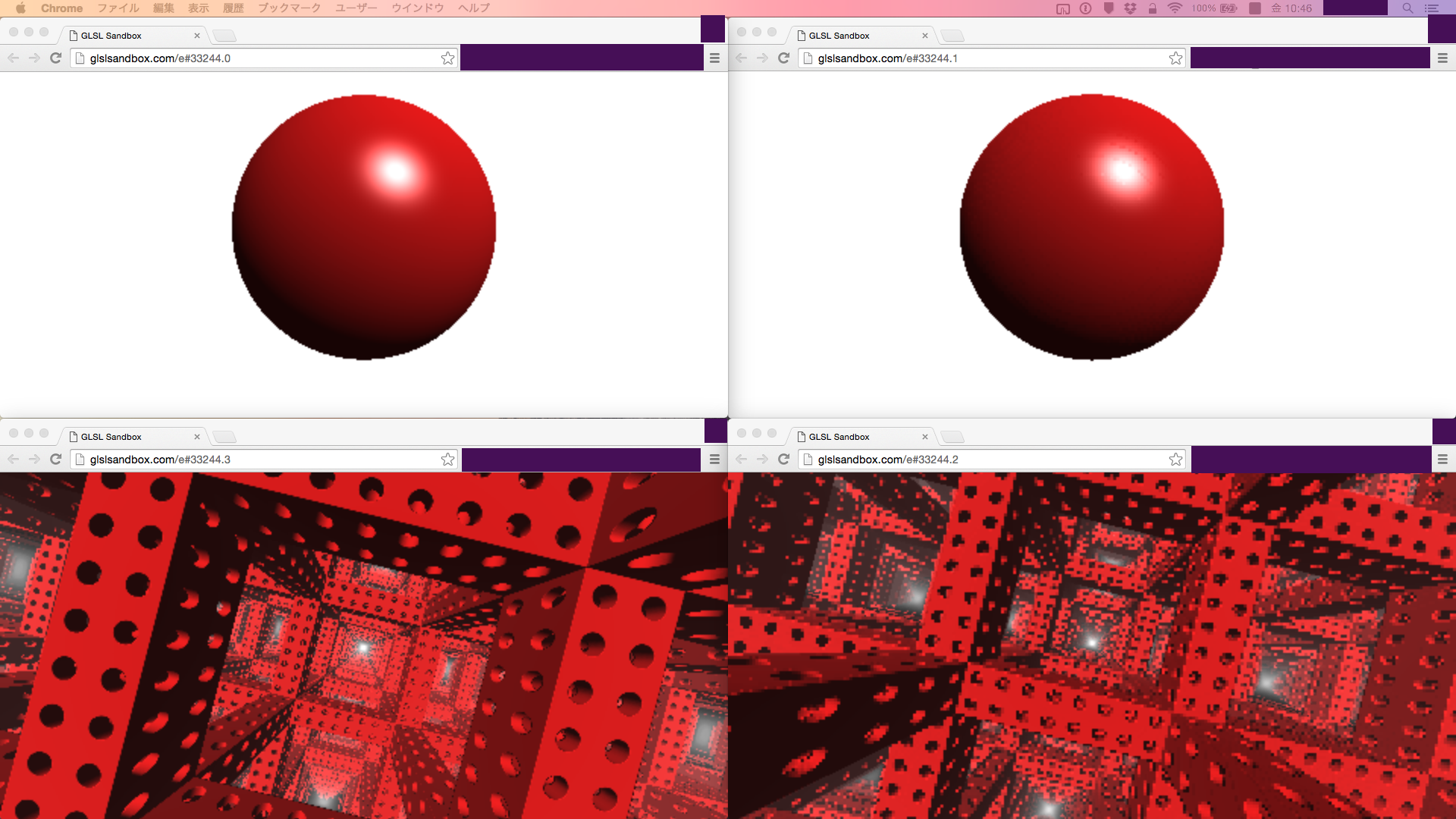
これはレイマーチングの例の比較した画像です。左側が距離関数の勾配による法線、右側がdFdx/dFfyによる法線です。
ただし、2x2にブロックに解像度が落ちてしまい、結果が汚くなるので、実用性があるかどうかは不明です。
距離関数の勾配による法線の導出
一般的にはレイマーチングの法線は距離関数の勾配で求めます。今まではこの方法しか見たことがありませんでした。
const float EPS = 0.001;
vec3 getNormal(vec3 p) {
return normalize(vec3(
sceneDist(p + vec3(EPS, 0.0, 0.0)) - sceneDist(p + vec3(-EPS, 0.0, 0.0)),
sceneDist(p + vec3(0.0, EPS, 0.0)) - sceneDist(p + vec3( 0.0, -EPS, 0.0)),
sceneDist(p + vec3(0.0, 0.0, EPS)) - sceneDist(p + vec3( 0.0, 0.0, -EPS))
));
}
距離関数は形状を陰関数表現したものとも言えます。また、陰関数における勾配が法線となる性質があります。
つまり、距離関数をワールド空間上のXYZに偏微分することで勾配が求まり、この勾配が法線ベクトルとなります。
詳しい話は、次のスライドの63ページあたりに簡単に解説しています。
dFdx/dFfyによる法線の導出
さて、本題のdFdx/dFfyによる法線の計算について説明します。
以前の記事のエッジ検出の例では、スカラー値の微分をしましたが、普通にベクトルも微分できます。
さらに微分する対象が画素値である必要も無いです。今回はレイと物体との交点の座標をスクリーン上で微分しています。
vec3 getNormal(vec3 p) {
vec3 dx = dFdx(p);
vec3 dy = dFdy(p);
return normalize(cross(dx, dy));
}
上の関数で法線が求まる仕組みを簡単に説明します。
物体の交点座標を微分すると接線になります。そして、XとYの2方向の接線があれば接平面が一意に決まり、接線の外積から法線も導出できるという仕組みです。
どちらの手法も偏微分で法線を求めますが、微分する対象が異なります。表にまとめるとこうなります。最終的にはどちらも法線になるのも面白いですね。
| 手法 | 偏微分される関数 | 偏微分する変数 | 偏微分した後の処理 |
|---|---|---|---|
| 距離関数の勾配による法線の計算 | 距離関数 | ワールド空間上のXYZ | 勾配(偏微分した値を並べる) |
| dFdx/dFdyによる法線の計算 | 交点座標 | スクリーン空間上のXY | 外積 |