鉄道路線データを可視化し、最短経路問題を解く (Python+Pandas+NetworkX)

はじめに

路線図とグラフネットワークの相性は良く、路線図で何か考えようとしたときに、だれでも思いつく最短経路問題について触れます。

鉄道の路線図を単純なグラフ問題に落とし込み、ダイクストラ法を使って最短経路を求めます。PythonのライブラリNetworkXにはダイクストラ法が組み込まれており、便利なので今回はそちらを採用します。

プログラムはGoogle Colaboratoryにアップロードしているのでブラウザ上で実行することができます。こちら
https://nbviewer.jupyter.org/github/galileo15640215/train/blob/master/train_dijkstra.ipynb

流れ

路線図とはいっても、いきなり全国のデータを扱うのは規模が大きすぎますし、全国の路線を考える前にまずは小規模の問題として東京メトロの路線を抽出し、作成します。

順番
・データの加工
・東京メトロ圏内の路線図
・東京メトロ圏内の最短経路
・全国の路線図
・全国の最短経路

必要なデータ

駅データ.jp https://ekidata.jp/ から
事業者データ company20200309.csv
路線データ line20200306free.csv
駅データ station20200316free.csv
接続駅データ join20200306.csv
をダウンロードします。(2020年5月1日現在のCSVファイル名)

こちらをもとに必要なデータを作っていきます。

プログラム

#必要なモジュール
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
import networkx as nx

#csvファイルからpandsa形式のテーブルを作成
station = pd.read_csv("station20200316free.csv")
join = pd.read_csv("join20200306.csv")
#pref = pd.read_csv("pref.csv")
line = pd.read_csv("line20200306free.csv")
company = ("company20200309.csv")

ここまで、必要なデータをPandasテーブルに入れました。

東京メトロ版

次に東京メトロのみのデータを抽出します。

#全国の駅から東京メトロの駅のみ抽出する 東京メトロ...company_cd == 18
metro = station[["station_cd", "station_name", "line_cd", "lon", "lat"]]
metro = pd.merge(metro, line, on = 'line_cd')
metro = metro[metro["company_cd"] == 18]
metro = metro[["station_cd", "station_name", "line_cd", "lon_x", "lat_x", "line_name", "line_color_c", "line_color_t"]]
lon = metro["lon_x"]
lat = metro["lat_x"]
metro["lon"] = lon
metro["lat"] = lat
metro = metro[["station_cd", "station_name", "line_cd", "lon", "lat", "line_name"]]

#東京メトロの接続辺を抽出する 路線...line_cd == 28001---28010
metro_join = join[(join["line_cd"]==28001)|(join["line_cd"]==28002)|(join["line_cd"]==28003)|(join["line_cd"]==28004)|(join["line_cd"]==28005)|(join["line_cd"]==28006)|(join["line_cd"]==28007)|(join["line_cd"]==28008)|(join["line_cd"]==28009)|(join["line_cd"]==28010)]
metro_join = metro_join[["station_cd1", "station_cd2"]]

ここから東京メトロの路線図のグラフを作成します。

#グラフの宣言
G = nx.Graph()
#頂点を駅名にする
G.add_nodes_from(metro["station_name"])
#plotの座標を設定
pos={}
for i, j, k in zip(metro["station_name"], metro["lon"], metro["lat"]):
  pos[i] = (j, k)
#リストeにstation_nameとstation_cdを格納し、リンクさせる
e = []
for i, j in zip(metro["station_name"], metro["station_cd"]):
  e.append([i, j])
#グラフに辺情報を加える
for i, j in zip(metro_join["station_cd1"], metro_join["station_cd2"]):
    for k in e:
      if k[1] == i:
        for l in e:
          if l[1] == j:
            G.add_edge(k[0], l[0])
#グラフの出力の設定
plt.figure(figsize=(10,10),dpi=200)
plt.title('東京メトロ', fontsize=20)
plt.axes().set_aspect('equal', 'datalim')
nx.draw_networkx(G, pos, node_color='b', alpha=0.8, node_size=10, font_size=5, font_family='IPAexGothic')
plt.show()

東京メトロの路線図を可視化することができました。ここから最短経路問題を解くために必要な情報をグラフに与えます。

グラフに情報を与える

#辺に重みとして駅間の距離を持たせるためのデータ作成
dist = []
cd1_lat = []
cd1_lon = []
cd2_lat = []
cd2_lon = []
not_exist = [] #joinテーブルには存在しているが、stationテーブルには存在していないstation_cdを格納
for i, j in zip(metro_join["station_cd1"], metro_join["station_cd2"]):
  flag = True
  for k, l, m in zip(metro["station_cd"], metro["lat"], metro["lon"]):
    if i == k:
      cd1_x = l
      cd1_y = m
      cd1_lat.append(l)
      cd1_lon.append(m)
      flag = False
    if j == k:
      cd2_x = l
      cd2_y = m
      cd2_lat.append(l)
      cd2_lon.append(m)
  if flag:
    not_exist.append([i, j])
    #print(i, j)
  else:
    dist.append(((cd1_x-cd2_x)**2 + (cd1_y-cd2_y)**2)**0.5)
#このまま実行するとエラー ValueError: Length of values does not match length of index
#どうやら"station_cd" == 2800701と2800702はstationテーブルに存在しておらず、joinテーブルから不要なので削除
#以下2行は...metro_join = metro_join[metro_join["station_cd1"] != 2800701]...と等価
for i in range(len(not_exist)):
  metro_join = metro_join[metro_join["station_cd1"] != not_exist[i][0]]
#joinテーブルに列を追加
metro_join["cd1_lat"] = cd1_lat
metro_join["cd1_lon"] = cd1_lon
metro_join["cd2_lat"] = cd2_lat
metro_join["cd2_lon"] = cd2_lon
metro_join["distance"] = dist

グラフに辺の重みを与えていきます

#nodes is station_name
#グラフに辺の重みを与える
for i, j, m in zip(metro_join["station_cd1"], metro_join["station_cd2"], metro_join["distance"]):
    for k in e:
      if k[1] == i:
        for l in e:
          if l[1] == j:
            G.add_edge(k[0], l[0], weight=m)

最短経路問題を解くために必要なNetworkXのライブラリ、Networkx.dijkstra_path()は日本語の頂点に対応していないようです。頂点をstation_nameからstation_cdへ変更し、新たにグラフを宣言します。

#nodes is station_cd
G = nx.Graph()
G.add_nodes_from(metro["station_cd"])
pos={}
for i, j, k in zip(metro["station_cd"], metro["lon"], metro["lat"]):
  pos[i] = (j, k)
for i, j, m in zip(metro_join["station_cd1"], metro_join["station_cd2"], metro_join["distance"]):
  G.add_edge(i, j, weight=m)
#station_cdを頂点にしたときに、同名のstation_nameでも路線ごとにstation_cdが設定されているため、このままでは他の路線との接続辺を持っていない
#そこで、重み0として同名の駅を接続させる
for i, j in zip(metro["station_name"], metro["station_cd"]):
  for k, l in zip(metro["station_name"], metro["station_cd"]):
    if i == k and j != l:
      G.add_edge(j, l, weight=0)

#スタートとゴールの駅を設定
st_name = "荻窪"
go_name = "西船橋"
#station_nameからstation_cdを検索
for i, j in zip(metro["station_name"], metro["station_cd"]):
  if i == st_name:
    st = j
  if i == go_name:
    go = j
#最短経路を探索
dij = nx.dijkstra_path(G, st, go)
out = []
for k in range(len(dij)):
  for i, j in zip(metro["station_name"], metro["station_cd"]):
    if j == dij[k]:
      out.append(i)
print(out)
#最短経路用のグラフを宣言
G_root = nx.Graph()
G_root.add_nodes_from(dij)
pos_root = {}
for l in dij:
  for i, j, k in zip(metro["station_cd"], metro["lon"], metro["lat"]):
    if l == i:
      pos_root[l] = (j, k)
for i in range(len(dij)-1):
  G_root.add_edge(dij[i], dij[i+1])

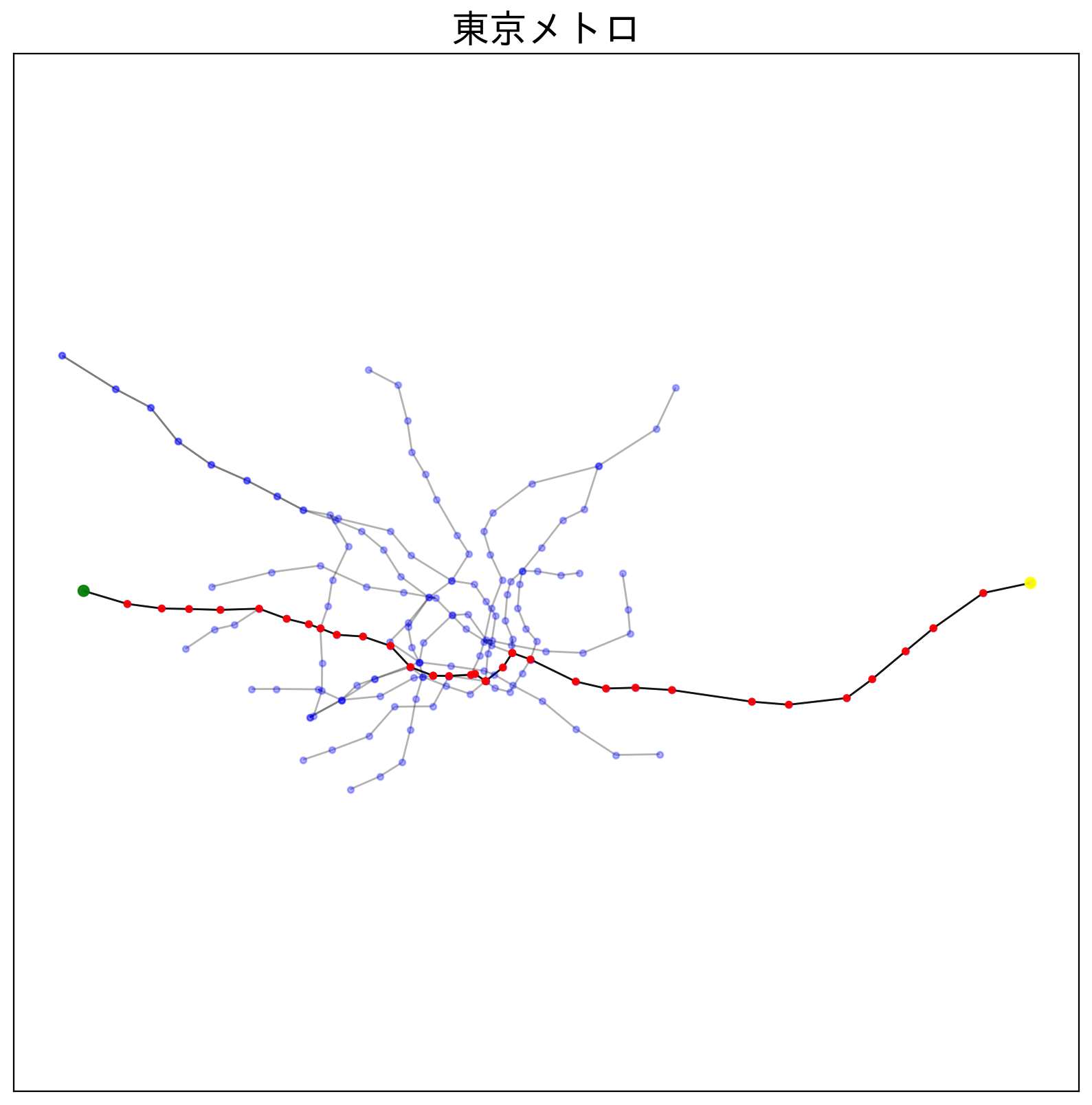
plt.figure(figsize=(10,10),dpi=200)
plt.title('東京メトロ', fontsize=20)
plt.axes().set_aspect('equal', 'datalim')
nx.draw_networkx(G, pos, node_color='b', alpha=0.3, node_size=10, with_labels= False)
c = ['green' if n==st else 'red' if n!=go else'yellow' for n in G_root.nodes()]
n_size = [30 if n==st else 10 if n!=go else 30 for n in G_root.nodes()]
nx.draw_networkx(G_root, pos_root, node_color=c, alpha=0.9, node_size=n_size, with_labels= False)
plt.show()

実行結果
['荻窪', '南阿佐ケ谷', '新高円寺', '東高円寺', '新中野', '中野坂上', '西新宿', '新宿', '新宿三丁目', '新宿御苑前', '四谷三丁目', '四ツ谷', '赤坂見附', '国会議事堂前', '国会議事堂前', '霞ケ関', '日比谷', '日比谷', '銀座', '銀座', '京橋', '日本橋', '日本橋', '茅場町', '門前仲町', '木場', '東陽町', '南砂町', '西葛西', '葛西', '浦安', '南行徳', '行徳', '妙典', '原木中山', '西船橋']

東京メトロでの最短経路を描画することができました。
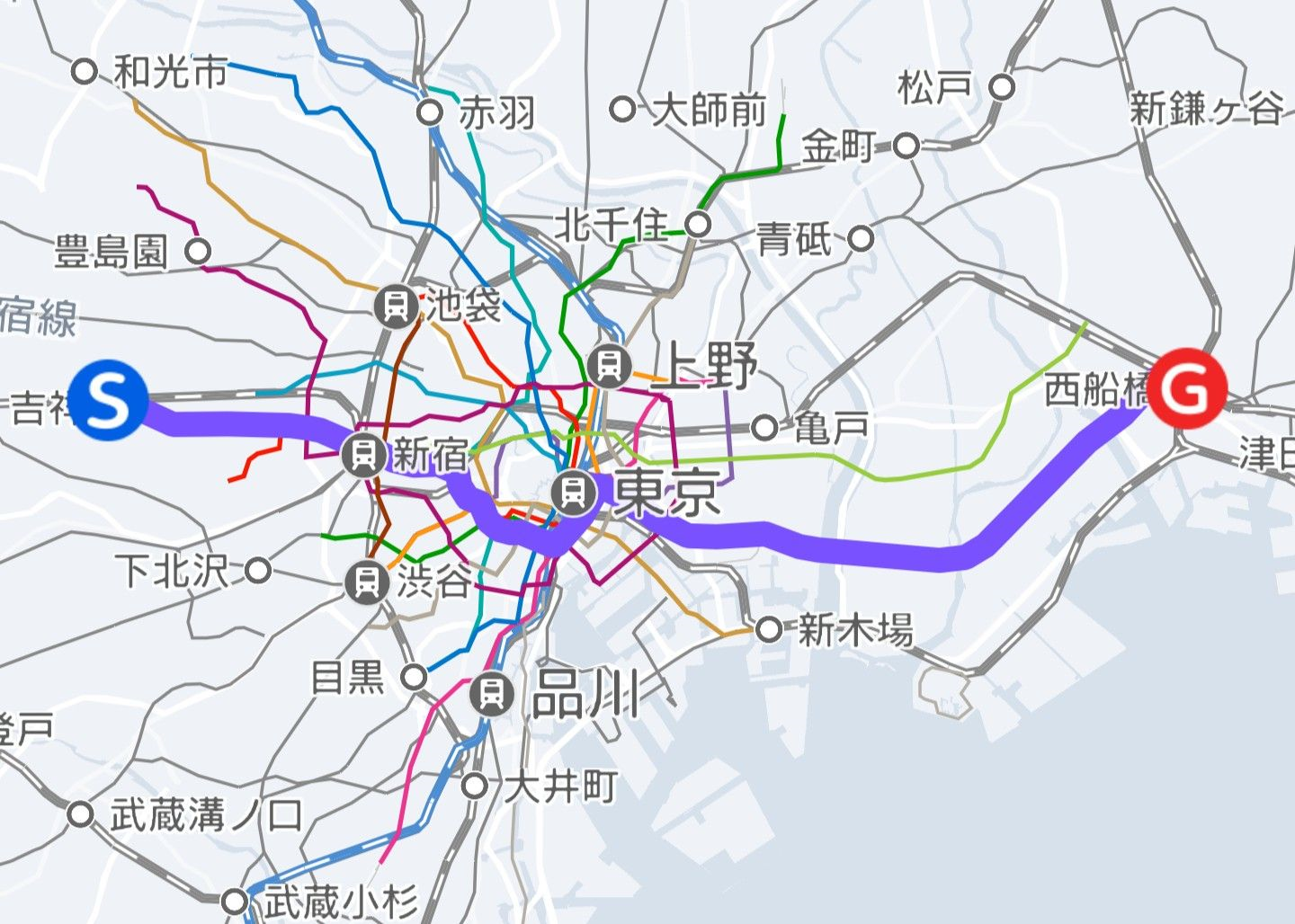
実際の優秀な乗換案内アプリと比べてどうでしょうか。

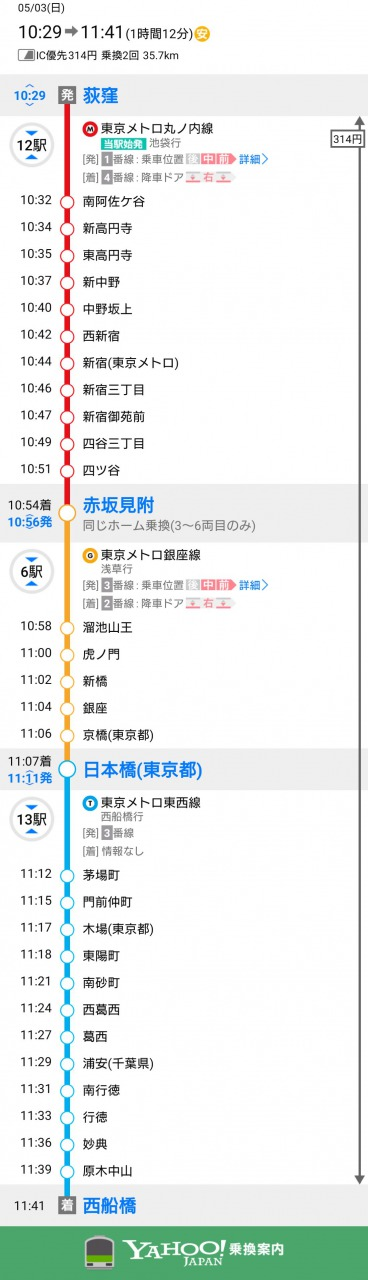
プログラムの方は乗換が多くなってしまっています。
ですが、東京メトロのような小規模なものだと経路はほぼ一致しています。

次に、全国版

全国でもやることは同じです。

zen_join = join
zen = station[["station_cd", "station_name", "line_cd", "lon", "lat"]]
zen = pd.merge(zen, line, on='line_cd')
zen = zen[["station_cd", "station_name", "line_cd", "lon_x", "lat_x", "line_name"]]
lon = zen["lon_x"]
lat = zen["lat_x"]
zen["lon"] = lon
zen["lat"] = lat
zen = zen[["station_cd", "station_name", "line_cd", "lon", "lat", "line_name"]]
cd1_lat = []
cd1_lon = []
cd2_lat = []
cd2_lon = []
dist = []
not_exist = []
for i, j in zip(zen_join["station_cd1"], zen_join["station_cd2"]):
  flag = True
  for k, l, m in zip(zen["station_cd"], zen["lat"], zen["lon"]):
    if i == k:
      cd1_x = l
      cd1_y = m
      cd1_lat.append(l)
      cd1_lon.append(m)
      flag = False
    if j == k:
      cd2_x = l
      cd2_y = m
      cd2_lat.append(l)
      cd2_lon.append(m)
  if flag:
    not_exist.append([i, j])
    #print(i, j)
  else:
    dist.append(((cd1_x-cd2_x)**2 + (cd1_y-cd2_y)**2)**0.5)
#stationテーブルに存在しておらず、joinテーブルから不要なので削除
for i in range(len(not_exist)):
  zen_join = zen_join[zen_join["station_cd1"] != not_exist[i][0]]# & zen_join["station_cd2"] != not_exist[i][1]]
zen_join["cd1_lat"] = cd1_lat
zen_join["cd1_lon"] = cd1_lon
zen_join["cd2_lat"] = cd2_lat
zen_join["cd2_lon"] = cd2_lon
zen_join["distance"] = dist

#nodes is station_cd
G = nx.Graph()
G.add_nodes_from(zen["station_cd"])
pos={}
for i, j, k in zip(zen["station_cd"], zen["lon"], zen["lat"]):
  pos[i] = (j, k)
for i, j, m in zip(zen_join["station_cd1"], zen_join["station_cd2"], zen_join["distance"]):
  G.add_edge(i, j, weight=m)
for i, j, m in zip(zen["station_name"], zen["station_cd"], zen["lat"]):
  for k, l, n in zip(zen["station_name"], zen["station_cd"], zen["lat"]):
    if i == k and j != l and m == n:
      #print(i, j, k, l)
      G.add_edge(j, l, weight=0)
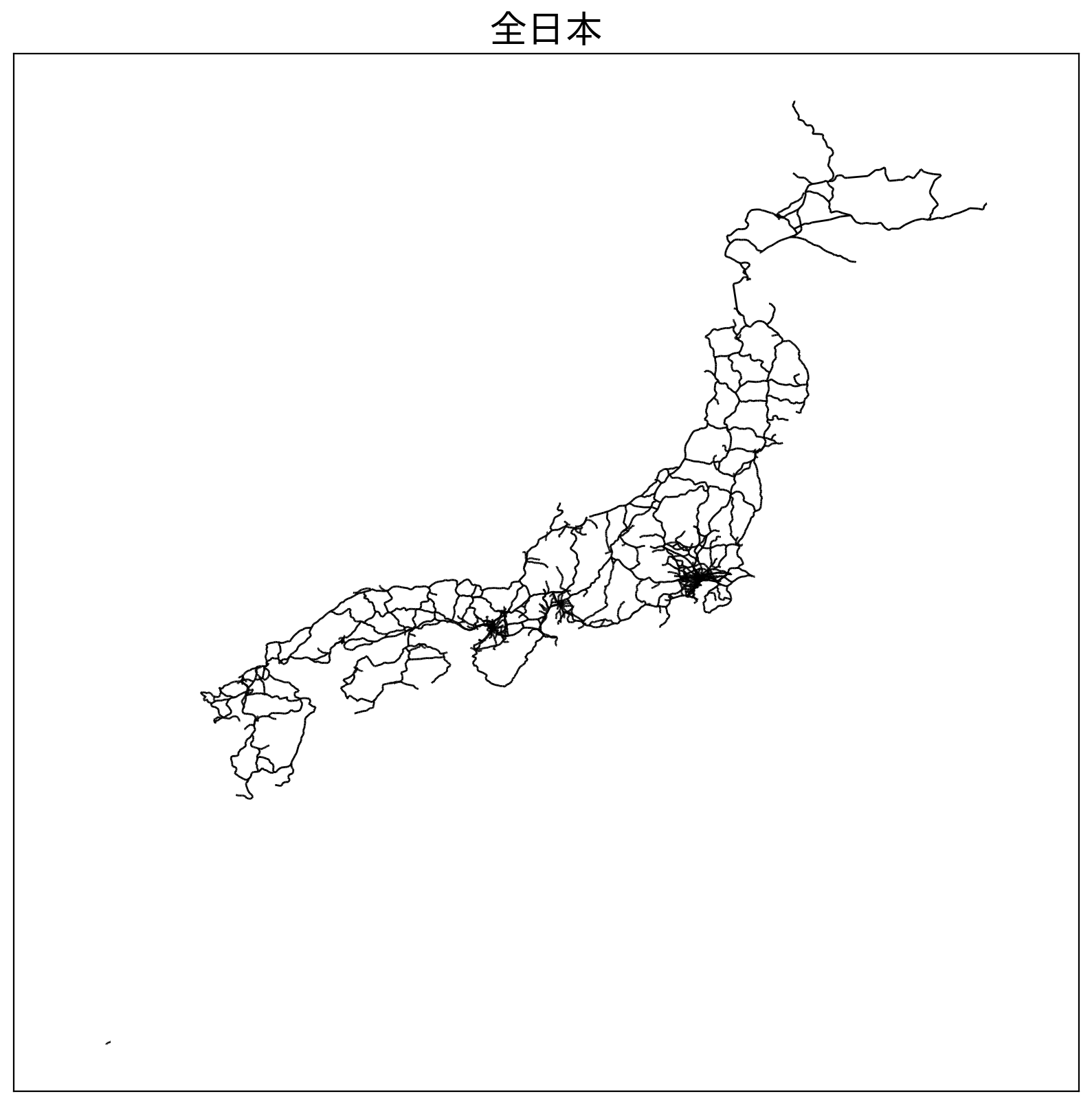
plt.figure(figsize=(10,10),dpi=200)
plt.title('全日本', fontsize=20)
plt.axes().set_aspect('equal', 'datalim')
nx.draw_networkx(G, pos, alpha=0.0, with_labels=False)
nx.draw_networkx_edges(G, pos)
plt.show()

st_name = "根室"
go_name = "鹿児島"
for i, j in zip(zen["station_name"], zen["station_cd"]):
  if i == st_name:
    st = j
  if i == go_name:
    go = j
dij = nx.dijkstra_path(G, st, go)
out = []
for k in range(len(dij)):
  for i, j in zip(zen["station_name"], zen["station_cd"]):
    if j == dij[k]:
      out.append(i)
print(out)

#nodes is station_cd
plt.figure(figsize=(50,50),dpi=200)
G_root = nx.Graph()
G_root.add_nodes_from(dij)
pos_root = {}
for l in dij:
  for i, j, k in zip(zen["station_cd"], zen["lon"], zen["lat"]):
    if l == i:
      pos_root[l] = (j, k)
for i in range(len(dij)-1):
  G_root.add_edge(dij[i], dij[i+1])

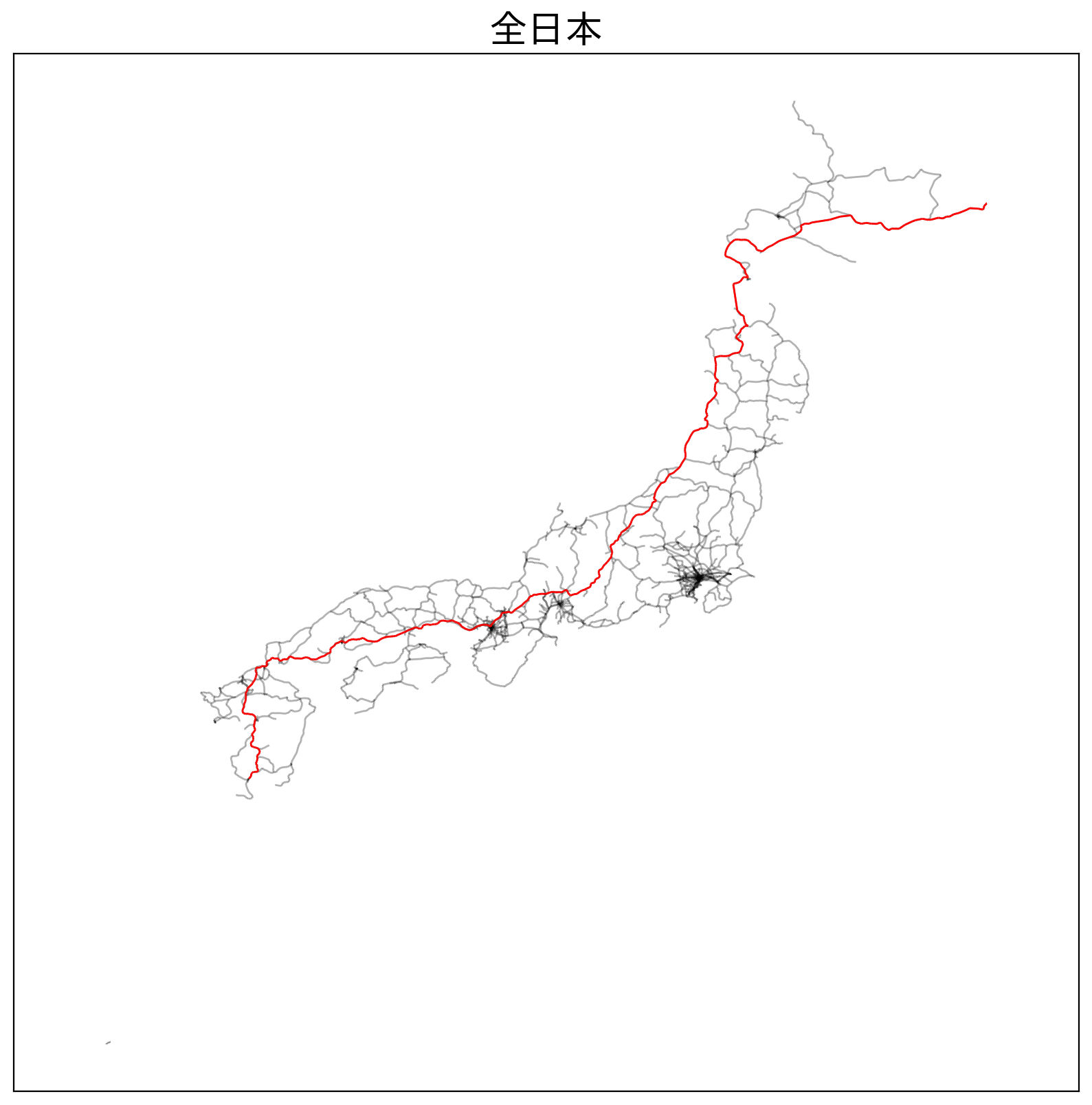
plt.figure(figsize=(10,10),dpi=200)
plt.title('全日本', fontsize=20)
plt.axes().set_aspect('equal', 'datalim')
nx.draw_networkx(G, pos, alpha=0.0, with_labels=False)
nx.draw_networkx_edges(G, pos, alpha=0.3)
nx.draw_networkx(G_root, pos_root, alpha=0.0, with_labels=False)
nx.draw_networkx_edges(G_root, pos_root, alpha=1.0, edge_color='r')
plt.show()

完成。実際に乗り継いでいくのは非現実的で、相当な電車好きでない限り地獄です。
できました。北海道新幹線のおかげで青函トンネルを通って本州まで行くことができます。
時間最短でいえば、東北新幹線、東海道新幹線を乗り継ぐのが当たり前ですが、経路最短の場合、東北新幹線を使わずに在来線で日本海側に出るようです。

まとめ

今回の辺情報は距離でしたが、それを時間にすると乗換案内の最短時間のようなものができます。時間データを作成出来たらやってみたいと思います。
To be continued...

参考にしたサイト

鉄道路線データをグラフとしてCytoscapeで可視化する 1
https://qiita.com/keiono/items/29286f49b15a5b13c987
駅データの加工はこちらを参考にしています。