はじめに
PCA(主成分分析)について勉強した内容をまとめています。
数学的な理論については前回の投稿に記載しています。今回は、Numpyのみを使用したPCAの自力実装を行い、sklearnの処理の再現を目指します。
参考
主成分分析の理解と実装に当たっては、下記を参考にさせていただきました。
- 多変量解析法入門 著者; 永田 靖, 棟近 雅彦 出版社; サイエンス社
- 多変量解析のはなし 著者; 有馬 哲, 石村 貞夫 出版社; 東京図書
- [sklearnのドキュメント]
(https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html)
PCAを自力実装する
今回使用するデータ
今回はsklearnの中にデータセットとして用意されている、ボストン住宅価格のデータセットを用いて検証を行います。
まず下記のように、データを読み込みます。
from sklearn.datasets import load_boston
import pandas as pd
# データの読み込み
boston = load_boston()
# pandasのデータフレーム形式に変換
df = pd.DataFrame(boston.data, columns=boston.feature_names)
各説明変数のデータのカラムはこのようになっています。
今回はこれらの変数の主成分の導出に取り組んでいきます。
| カラム | 説明 |
|---|---|
| CRIM | 町ごとの一人当たりの犯罪率 |
| ZN | 宅地の比率が25,000平方フィートを超える敷地に区画されている。 |
| INDUS | 町当たりの非小売業エーカーの割合 |
| CHAS | チャーリーズ川ダミー変数(川の境界にある場合は1、それ以外の場合は0) |
| NOX | 一酸化窒素濃度(1000万分の1) |
| RM | 1住戸あたりの平均部屋数 |
| AGE | 1940年以前に建設された所有占有ユニットの年齢比率 |
| DIS | 5つのボストンの雇用センターまでの加重距離 |
| RAD | ラジアルハイウェイへのアクセス可能性の指標 |
| TAX | 10,000ドルあたりの税全額固定資産税率 |
| PTRATIO | 生徒教師の比率 |
| B | 町における黒人の割合 |
| LSTAT | 人口当たり地位が低い率 |
| MEDV | 1000ドルでの所有者居住住宅の中央値 |
理論編の復習
主成分の求め方の復習をします。
| 個体と変数 | $x_{1}$ | $x_{2}$ | ・・・ | $x_{p}$ |
|---|---|---|---|---|
| 1 | $x_{11}$ | $x_{21}$ | ・・・ | $x_{p1}$ |
| 2 | $x_{12}$ | $x_{22}$ | ・・・ | $x_{p1}$ |
| ・・・ | ・・・ | ・・・ | ||
| n | $x_{1n}$ | $x_{2n}$ | ・・・ | $x_{pn}$ |
このようなデータがあった時、まずデータの分散共分散行列$S$を求めます。
{
\begin{split}\begin{aligned}
s=
\begin{bmatrix}
s_{1}^2 & s_{12} & \cdots & s_{1p} \\
s_{12} & s_{2}^2 & \cdots & s_{2p} \\
\vdots \\
s_{1p} & s_{2p} & \cdots & s_{p}^2
\end{bmatrix} \\
\end{aligned}\end{split}
}
そして、この分散共分散行列$S$の固有値$\lambda$とその固有ベクトルを求めます。
{
\begin{split}\begin{aligned}
\begin{bmatrix}
s_{1}^2 & s_{12} & \cdots & s_{1p} \\
s_{12} & s_{2}^2 & \cdots & s_{2p} \\
\vdots \\
s_{1p} & s_{2p} & \cdots & s_{p}^2
\end{bmatrix} \\
\end{aligned}\end{split}
\begin{split}\begin{aligned}
\begin{bmatrix}
a_{i1} \\
a_{i2} \\
\vdots \\
a_{1p}
\end{bmatrix}
\end{aligned}\end{split}
=
\begin{split}\begin{aligned}
\lambda_{i}
\begin{bmatrix}
a_{i1} \\
a_{i2} \\
\vdots \\
a_{1p}
\end{bmatrix}
\end{aligned}\end{split}
}
こちらは変数の数だけ固有値を持ち、固有値を下記のように並べ替えた時に**最大固有値に属する固有ベクトルから順に第1主成分の係数、第2主成分の係数...**という感じになっていくのでした。
$\lambda_{1} \geq \lambda_{2} \geq \lambda_{3} \dots \geq \lambda_{p} \geq 0$
より詳細な解説は前回の投稿の投稿をご確認ください。
今回は、こちらの処理をPythonで実装していきます。
主成分分析モデルの実装
下記が主成分分析モデルの自力実装を行った結果です。
class PCA:
def __init__(self):
#データの標準化
self.standardscaler = None
#分散共分散行列
self.v_cov = None
#固有値
self.eig = None
#固有ベクトル
self.eig_vec = None
def fit(self, x):
#データを標準化する
self.standardscaler = (x - x.mean())/x.std(ddof=0)
#データの分散共分散行列を求める
self.v_cov = np.cov(self.standardscaler.T, bias = 0)
#分散共分散行列の固有値と固有ベクトルを求める
self.eig, self.eig_vec = np.linalg.eig(self.v_cov)
#各主成分と変数の固有ベクトルをマトリクス化
self.pca_matrix = pd.DataFrame(self.eig_vec.T, columns = df.columns)
self.pca_matrix.index = ['PC' + str(i+1) for i in self.pca_matrix.index]
self.pca_matrix = self.pca_matrix.T
self.pca_matrix.loc['固有値'] = list(self.eig)
#寄与率を求める
self.pca_matrix.loc['寄与率'] = self.pca_matrix.loc['固有値'] / self.pca_matrix.loc['固有値'].sum()
self.pca_matrix['']=(['固有ベクトル']*len(la) + ['',''])
self.pca_matrix = self.pca_matrix.set_index('', append = True).swaplevel()
def transfer(self, n_components):
#PCA(主成分)空間にデータを写像する
return np.dot(self.standardscaler, self.eig_vec[:,:n_components])
検証
上記の自力実装のモデルと、sklearnの結果が一致しているか検証します。
自力実装の結果
ボストン住宅価格のデータセットの説明変数の主成分分析を行います。
pca = PCA()
pca.fit(df)
pca.pca_matrix
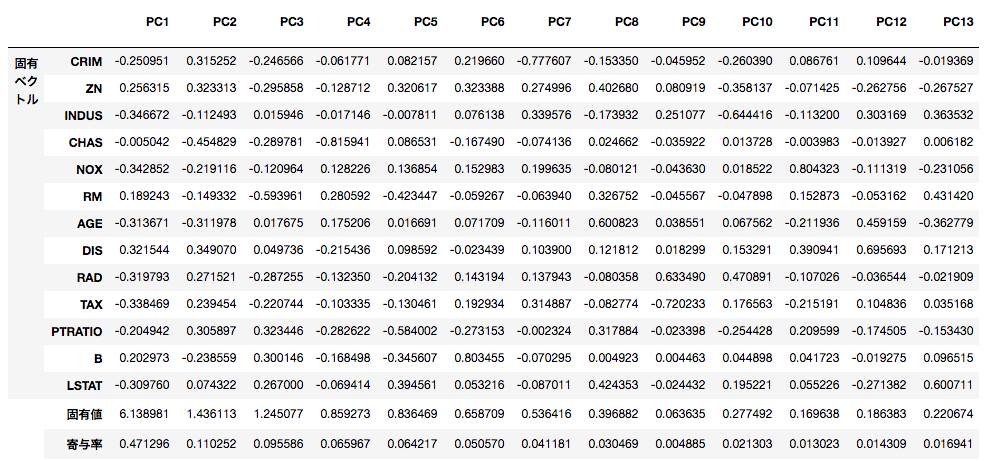
まず、下記のような形に出力できるようにしました。
各主成分の固有ベクトル、固有値、寄与率を一目で見ることができます。
続いて、主成分空間への写像(次元の圧縮)を行います。
今回は13次元ある変数を3次元に圧縮します。
print(pca.transfer(n_components = 3))
すると出力はこのような感じになります。
[[ 2.09829747 -0.77311275 -0.34294273]
[ 1.45725167 -0.59198521 0.69519931]
[ 2.07459756 -0.5996394 -0.1671216 ]
...
[ 0.31236047 -1.15524644 0.40859759]
[ 0.27051907 -1.04136158 0.58545406]
[ 0.12580322 -0.76197805 1.294882 ]]
無事に3次元に圧縮できているようです。
続いて、sklearnでも同様の結果が出ているかを検証します。
sklearnの結果
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# データの標準化を行う
st = StandardScaler()
st.fit(df)
df_ss = st.transform(df)
# データの標準化を行う
pca = PCA(n_components = 3)
pca.fit(df_sk)
# 固有値を出力
print(pca.explained_variance_)
# 寄与率を出力
print(pca.explained_variance_ratio_)
出力するとこのような感じになります。
一行目が第4主成分までの固有値、二行目が第4主成分までの寄与率です。
自力実装のモデルで導出した数値と一致していることがわかります。
[6.1389812 1.43611329 1.2450773 ]
[0.47129606 0.11025193 0.0955859 ]
それでは、sklearnのモデルで主成分空間に写像(次元圧縮)してみます。
print(pca.transform(df_norm))
出力はこちら。
符号自体は逆になっているのですが、それ以外は一致しています。
符号についてですが、逆であっても問題なく次元圧縮できていると捉えて問題ありません。
sklearnの場合、導出した固有ベクトルの符号自体が既に自力実装のものと逆になっているのですが、そもそも固有ベクトルのスカラー倍は全て固有ベクトルなので、その時点で$-1$倍してしまえば完全に一致します。
(という認識で合っているはずなのですが、問題あればご指摘ください。。。)
[[-2.09829747 0.77311275 0.34294273]
[-1.45725167 0.59198521 -0.69519931]
[-2.07459756 0.5996394 0.1671216 ]
...
[-0.31236047 1.15524644 -0.40859759]
[-0.27051907 1.04136158 -0.58545406]
[-0.12580322 0.76197805 -1.294882 ]]
また、実はsklearnでは固有値ではなく特異値(SVD)という考え方を用いて主成分を導出しています。
この条件下では等価な処理をしているという認識で問題ないようなのですが、データが異なってくると処理が変わってくる場合があるようなので、ここは引き続き勉強していこうと思います。
Next
特異値分解など他の次元圧縮系のアルゴリズムの理解も深めていきたいですが、また別系統の機械学習アルゴリズムに手を出していくかもしれないです。