凝集型(階層型)クラスタリングを理解する

#はじめに
凝集型クラスタリングについて勉強した内容をまとめました。
最も簡単で基礎的なクラスタリングアルゴリズムです。

##参考
凝集型クラスタリングの理解に当たって下記を参考にさせていただきました。

• 言語処理のための機械学習入門 (自然言語処理シリーズ)　高村 大也 (著), 奥村 学 (監修)　出版社; コロナ社
• sklearnの凝集型クラスタリングについてのドキュメント　
• scipyの凝集型クラスタリングについてのドキュメント　

#階層型クラスタリング概要
##凝集型クラスタリングとは何か
「単純に最も似ているもの同士をくっつければいいのでは？」という人間的な直感をそのままクラスタリング手法に当てはめたアルゴリズムがこの**「凝集型クラスタリング」**です。
一般的には凝集した状態を上、ばらばらの状態を下とみなすので、**ボトムアップクラスタリング(bottom-up clustering)**とも呼ばれています。

はじめは下記(a)のようにバラバラの状態にあり、この時点では全てはたがいに異なるクラスタに属しています。そこから(b)→(c)→(d)と進むに従って少しずつ大きなクラスタが形成されていきます。

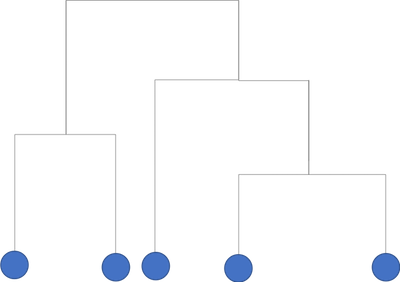
また、このプロセスを一つの図で表したものが**樹形図(dendrogram)**です。

クラスタリングのプロセスは樹形樹の下から上に向かって進みます。
二つの線が交わっている箇所でクラスタ同士の融合が起こります。交わる箇所の高さが融合の順序を表していて、低いほど先に融合が発生したことを表しています。
この樹形樹をある高さで切るとクラスタの集合が得られます。

##クラスター同士の距離の測り方
各ベクトル同士の類似度であれば、単純にそのベクトル同士のユークリッド距離で計算すれば問題ありません。ただ、それが**複数のベクトルから成るクラスター同士の類似度であればその測り方は自明ではありません。**以下ではクラスタ同士の類似度を測るための主要な方法をご紹介します。

• クラスター$u$とクラスター$v$の距離を$d(u,v)$と表記します。
• クラスター$u$は$|u|$個のベクトルで構成されており、中には各ベクトル$u[1],...,u[|u|-1]$が含まれているとします。クラスター$v$もクラスター$v$の場合と同様とします。
• 各ベクトル同士の距離は$dist(u[1],v[1])$といったように記載します。

###単純連結法(single-link method)

d(u,v) = \min(dist(u[i],v[j]))

ベクトル$i$はクラスター$u$内のベクトルで、ベクトル$j$はクラスター$v$内のベクトルです。
各々のクラスターの中で最も近いベクトル同士の距離をそのクラスター同士の距離とする方法です。

###完全連結法(complete-link method)

d(u,v) = \max(dist(u[i],v[j]))

ベクトル$i$はクラスター$u$内のベクトルで、ベクトル$j$はクラスター$v$内のベクトルです。
各々のクラスターの中で最も遠いベクトル同士の距離をそのクラスター同士の距離とする方法です。

###重心法(centroid)

c_{u} = \frac{1}{|u|}\sum_{i=1}^{|u|} u[i] \\
c_{v} = \frac{1}{|v|}\sum_{i=1}^{|v|} u[v] \\
d(u,v) =  dist(c_{u},c_{v})

ベクトル$c_{u}$とベクトル$c_{v}$はそれぞれクラスター$u$とクラスター$v$の重心ベクトルです。
各々のクラスターの重心ベクトル同士の距離をそのクラスター同士の距離とする方法です。

###ウォード法(centroid)

d(u,v) =  L(u \cup v) - L(u) -L(v) 

$L(u)$と$L(v)$はそれぞれクラスターの重心とクラスター内の各サンプルとの距離の距離の2乗和を表しています。また、$L(u \cup v)$はクラスター$u$とクラスター$v$が結合した時のクラスターの重心とクラスター内の各サンプルとの距離の2乗和を表しています。
ウォード法は2つのクラスターを統合する際に、クラスター内の平方和が最小となるようにクラスターを形成する手法になっています。

###クラスター同士の距離の測り方まとめ
クラスター同士の距離の測り方として主要なものを紹介しました。sklearnやscipyのライブラリでは引数でどの手法を使用するか選択できます。どちらもデフォルトではウォード法が指定されており、ウォード法が最も汎用的に使用できる手法とされているようです。

#階層型クラスタリングをライブラリを用いて実装
##使用するデータセット
今回はsklearnで読み込むことができるirisのサンプルデータセットを使います。
こちらはアヤメの品種についてのデータセットで、「target」と「target_names」には花の種類分けとそれぞれの名前が格納されており、「data」 には 4 つの特徴量(ガクの長さ、幅、花弁の長さ、幅)が格納されています。

import pandas as pd
import numpy as np
import scipy
from sklearn import datasets

dataset = datasets.load_iris()
dataset_data = dataset.data
dataset_target = dataset.target
target_names = dataset.target_names

##クラスターの形成
まずはscipyを用いて階層型クラスタリングを行います。

from scipy.cluster.hierarchy import linkage,dendrogram,fcluster
#引数でウォード法を指定
Z = linkage(dataset_data, method='ward', metric='euclidean')
pd.DataFrame(Z)

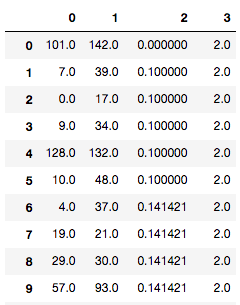
ここの処理で出力されるZの中身ですが、下記のようになっています。
1列と2列目が結合されたクラスターの番号、3列目がそのクラスター間の距離、4列目が結合後に新しくできたクラスターの中に入っている元のデータの数を表します。

##樹形図の描画
下記で樹形図を描画することが可能です。

import matplotlib.pyplot as plt
fig2, ax2 = plt.subplots(figsize=(20,5))
ax2 = dendrogram(Z)
fig2.show()

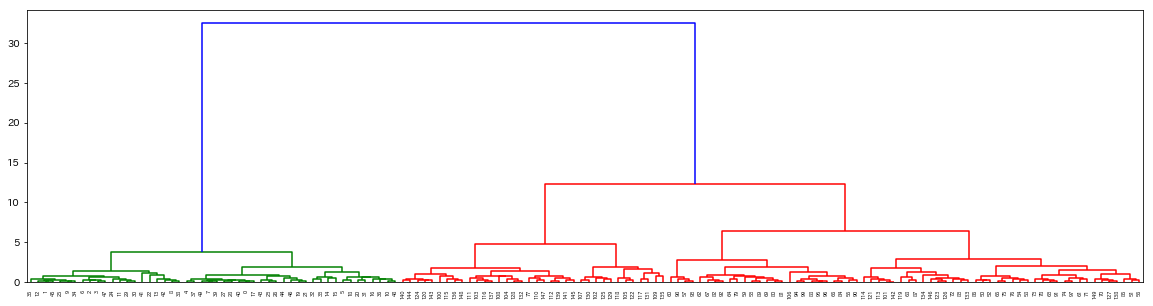
出力はこちらです。
下の方が非常に細かくて見づらくなっていますが、階層構造に描画できていることがわかります。

##クラスタリングを実施
下記でクラスタリングを実施することが可能です。

#引数のcriterionにてクラスタリングのやり方を指定
#引数のtで閾値を指定（今回は最大クラスタ数を指定）
F = fcluster(Z, t = 3, criterion = 'maxclust')
print(F)

出力はこちらです。それぞれのデータにクラスタリングされたラベルが貼られていることがわかります。

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
       3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
       3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 2, 2, 2, 2, 3, 2, 2, 2,
       2, 2, 2, 3, 3, 2, 2, 2, 2, 3, 2, 3, 2, 3, 2, 2, 3, 3, 2, 2, 2, 2,
       2, 3, 3, 2, 2, 2, 3, 2, 2, 2, 3, 2, 2, 2, 3, 2, 2, 3], dtype=int32)

ちなみに、sklearnでも同様のクラスタリングが可能です。

from sklearn.cluster import AgglomerativeClustering
agg = AgglomerativeClustering(n_clusters = 3)
print(agg.fit_predict(dataset.data))

同様の結果が出力されていることがわかります。

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2,
       2, 2, 2, 0, 0, 2, 2, 2, 2, 0, 2, 0, 2, 0, 2, 2, 0, 0, 2, 2, 2, 2,
       2, 0, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0])

ちなみにsklearnでは樹形図を描画することができないので、樹形図を描画されたい方はscipyを使用してください。

#Next
次はクラスタリングアルゴリズムの王道、「k-means法」についてまとめたいと思います。