はじめに
統計を勉強していると必ず出てくる指数分布ですが、例の確率分布の式が中々頭に入ってこなかったので確率分布の導出から丁寧に追って理解しようと考えました。イメージを掴むためにPythonで描画も行います。
参考
指数分布の理解とその分布の描画を行うに当たって下記を参考にさせていただきました。
- 【大学数学】指数分布(具体例やその意味、ポアソン分布との関係)【確率統計】
- 統計学入門 (基礎統計学Ⅰ) 東京大学教養学部統計学教室
- Maximum Likelihood for the Exponential Distribution, Clearly Explained! V2.0
指数分布の理解
指数分布とは何か
\begin{equation}
f(x)=
\left\{
\begin{aligned}
&\lambda \mathrm{e}^{-\lambda x} &(x\geq0) \\
&0 &(x<0)\\
\end{aligned}
\right.
\end{equation}
指数分布とは単位時間当たりに平均$\lambda$回起こる事象の発生間隔が$x$単位時間である確率を表す確率分布です。確率密度関数は上記のように与えられます。
指数分布は下記のような例に用いられます。
- 災害が発生する間隔
- 故障時間が一定であるシステムの偶発的な故障が発生する間隔
- 店においてある客が来てから次の客が来るまでの間隔
また、期待値が$\frac{1}{\lambda}$で分散が$\frac{1}{\lambda^2}$であるという性質があります。
指数分布のかたち
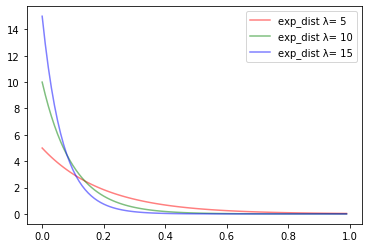
それでは実際に分布を描画します。
下記の3つの例を考えて「次の客が来店するまでの時間間隔の確率分布」を描画してみます。
- 1時間当たり平均5人が来店する店($\lambda = 5$)
- 1時間当たり平均10人が来店する店($\lambda = 10$)
- 1時間当たり平均15人が来店する店($\lambda = 15$)
import numpy as np
import matplotlib.pyplot as plt
def exp_dist(lambda_, x):
return lambda_ * np.exp(- lambda_*x)
x = np.arange(0, 1, 0.01)
y1= [exp_dist(5,i) for i in x]
y2= [exp_dist(10,i) for i in x]
y3= [exp_dist(15,i) for i in x]
plt.plot(x, y1, color="red"
,alpha=0.5, label="exp_dist λ= %d" % 5)
plt.plot(x, y2, color="green"
,alpha=0.5, label="exp_dist λ= %d" % 10)
plt.plot(x, y3, color="blue"
,alpha=0.5, label="exp_dist λ= %d" % 15)
plt.legend()
plt.show()
**$\lambda$の値が小さければ小さいほど減少の仕方は緩やかになりますが$\lambda$の値がどうであれ必ず単調減少する、というところがポイントです。**間隔的にも1時間で平均5人お客さんが来る店よりも、平均15人来る店の方が、次のお客さんが間隔空けずにすぐに来るであろうということがわかると思います。
また更にポイントなのが**$\lambda$の値がどうであれ$x=0$に近いほど確率密度が高くなるということです。すぐに次のお客様が来る確率が最も高いというのはおかしいのではないか?という違和感がある方もいらっしゃると思いますが、これは指数分布の無記憶性**という性質に由来しています。何かが1回起きたかから次も起きやすいということではなくて、完全にランダムで発生している事象と捉えるため、発生しない時間がずっと続くよりもすぐに発生する確率の方が高くなるということです。(前の事象が発生したか否かについては完全に忘れ去れているという意味で無記憶)
指数分布の累積分布関数
私たちの日常の感覚としてより知りたいのは、次のお客さんがきっかり10分後に来る確率、よりも10分以内に来る確率の方だと思います。そこで事象の発生間隔が$x$単位時間以内である確率を考えます。確率を足し合わせる、つまり積分をして求める必要があります。
{\begin{eqnarray}
F(x) &=& \int_0^x f(x) dx \\
&=& \int_0^x \lambda \mathrm{e}^{-\lambda x} dx \\
&=& \lambda\int_0^x \mathrm{e}^{-\lambda x} dx \\
&=& \lambda\left[\frac{1}{-\lambda}\mathrm{e}^{-\lambda x}\right]^x_0 \\
&=& -\mathrm{e}^{-\lambda x} - (-1) \\
&=& 1 - \mathrm{e}^{-\lambda x} \\
\end{eqnarray}}
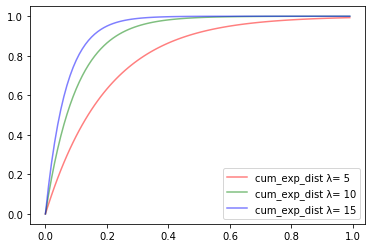
この累積分布関数もまた下記の3つの例を考えて描画してみます。
- 1時間当たり平均5人が来店する店($\lambda = 5$)
- 1時間当たり平均10人が来店する店($\lambda = 10$)
- 1時間当たり平均15人が来店する店($\lambda = 15$)
def cum_exp_dist(lambda_, x):
return 1 - np.exp(-lambda_ * x)
x = np.arange(0, 1, 0.01)
y1= [cum_exp_dist(5,i) for i in x]
y2= [cum_exp_dist(10,i) for i in x]
y3= [cum_exp_dist(15,i) for i in x]
plt.plot(x, y1, color="red"
,alpha=0.5, label="cum_exp_dist λ= %d" % 5)
plt.plot(x, y2, color="green"
,alpha=0.5, label="cum_exp_dist λ= %d" % 10)
plt.plot(x, y3, color="blue"
,alpha=0.5, label="cum_exp_dist λ= %d" % 15)
plt.legend()
plt.show()
このような1を最大値として単調増加しているグラフになることがわかります。
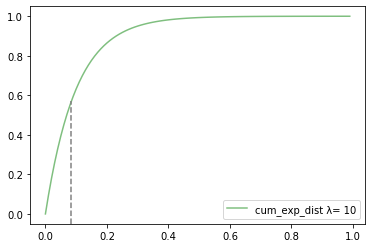
1つ具体例をあげて確率を計算してみます。
ex)1時間に平均10人来店する店で5分以内に次のお客さんが来店する確率
{\begin{eqnarray}
F(x) &=& 1 - \mathrm{e}^{-10・\frac{1}{12}} \\
&=& 0.565
\end{eqnarray}}
グラフ上では下記のポイントにあたります。
指数分布の導出
それでは指数分布の導出を考えていきます。
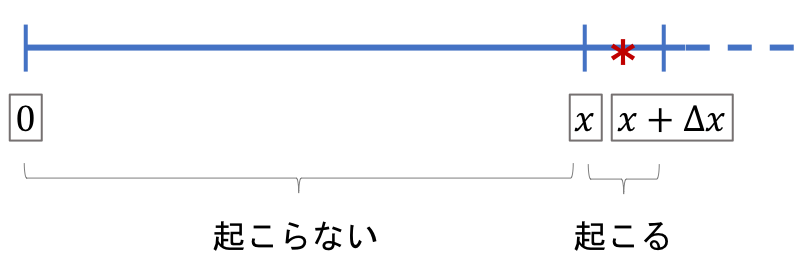
時間$x$までは事象が発生しない状況が続き、$x$と$x+Δx$の区間で初めて事象が発生すると考えます。($Δx$は微小区間)その時、$x$と$x+Δx$の区間で初めて事象が発生する確率は下記の等式で表すことができます。
f(x)Δx = (1 - F(x))・\lambdaΔx
$f(x)Δx$はそもそもの確率密度関数の定義から$Δx$の間に事象が発生する確率を表しているとわかります。また右辺は$x$までに事象が発生しない確率($(1 - F(x))$)と、$x$から$x+Δx$の間に事象が発生する確率($\lambdaΔx$)を掛け合わせています。
無記憶性により、$x$までに事象が発生する確率と$x$から$x+Δx$の間に事象が発生する確率は独立であるため、そのまま掛け合わせることができます。
それでは$\lambdaΔx$がどこから来ているのかを以下で書いていきます。
微小区間$Δx$は1単位時間を$n$等分($n$は十分に大きい)しているものなので下記が成り立ちます。
Δx・n=1
今回は単位時間に平均$\lambda$回起こる事象を考えてることから、上記式を用いて各々の微小区間において事象が発生する確率を考えると以下のようになります。
p = \frac{\lambda}{n} = \lambdaΔx
これで$\lambdaΔx$の意味がわかりました。それでは最初にあげた式を展開していきます。
{\begin{eqnarray}
f(x)Δx &=& (1 - F(x))・\lambdaΔx \\
f(x)&=& \lambda - \lambda F(x) \\
f'(x)&=& -\lambda f(x)
\end{eqnarray}}
2行目から3行目の展開では両辺を$x$で微分しています。
$f'(x)= -\lambda f(x)$は微分方程式の形になっていますが、微分をしても形が変わらない関数であるということを考えると簡単に指数関数であることがわかります。
f(x) = C・\mathrm{e}^{-\lambda x}
$C$は定数なので何でもよいのですが、これを積分すると累積分布関数になる必要があります。従って、必然的に$\int_0^∞f(x)=1$であるという制約がかかります。その制約を用いて定数$C$の値を定めます。
{\begin{eqnarray}
\int_0^∞f(x) &=& \int_0^∞ C・\mathrm{e}^{-\lambda x} \\
&=& C\int_0^∞ \mathrm{e}^{-\lambda x} \\
&=& C\left[\frac{1}{-\lambda}\mathrm{e}^{-\lambda x}\right]^∞_0 \\
&=& C\left[\frac{1}{-\lambda}\mathrm{e}^{-\lambda x}\right]^∞_0 \\
&=& -C(\frac{1}{-\lambda})\\
&=& \frac{C}{\lambda}\\
\\
1 &=& \frac{C}{\lambda}
\end{eqnarray}}
$\int_0^∞f(x)=1$という制約があるため、
{\begin{eqnarray}
1 &=& \frac{C}{\lambda} \\
C &=& \lambda \\
\end{eqnarray}}
上記から$f(x) = \lambda \mathrm{e}^{-\lambda x}$を導き出すことができました。
指数分布のパラメータの最尤推定
続いて指数分布のパラメータの最尤推定を考えていきます。
最尤推定とはあるパラメータ$\theta$に従う確率密度関数を$f(x;\theta)$とした時、尤度関数$L(\theta;x)=f(x;\theta)$が最大となるような推定量$\theta=\hat\theta$を最尤推定量と呼びます。
$\lambda = \theta$の指数分布に独立に従うを乱数を生成した時$x_1,x_2,\cdots,x_n$が出力されたとします。この時の$\lambda = \theta$の最尤推定量を考えます。
L(\theta ; x) = \theta \mathrm{e}^{-\theta x}
今回データが$x_1,x_2,\cdots,x_n$と$n$個与えられており、それらはすべて独立に生成されたものであるため、尤度関数は下記のように表すことができます。
\begin{eqnarray*}L(\theta ;x_1,x_2,\cdots,x_n)=
L(\theta ;x_1)×L(\theta ;x_2)×\cdots ×L(\theta ;x_n)
\end{eqnarray*}
上記を指数分布に当てはめると下記のようになります。
\begin{eqnarray*}L(\mu,\sigma ;x_1,x_2,\cdots,x_n)=
\displaystyle\prod_{k=1}\theta\mathrm{e}^{-\theta x}
\end{eqnarray*}
上記尤度関数が最大になるような$\theta$を求めればよいのですが、対数尤度関数に変換してその最大値を求めるタスクに置き換えても同様な結果が得られるため、対数尤度関数に変換します。
\begin{eqnarray*}
\log(L(\mu,\sigma ;x_1,x_2,\cdots,x_n))&=&
\log(n\theta) + \log( \mathrm{e}^{-\theta (x_1 + x_2 + \cdots, + x_n)}) \\
&=& n\log(\theta) -\theta (x_1 + x_2 + \cdots, + x_n) \\
\end{eqnarray*}
$ l(\theta)=\log (L(\theta ;x_1,x_2,\cdots,x_n))$と置いて$l(\theta)$を$\theta$で微分します。
{\begin{eqnarray*}
\frac{\partial l(\theta)}{\partial\theta}&=&\frac{\partial}{\partial\theta}(n\log(\theta) -\theta (x_1 + x_2 + \cdots, + x_n)) \\
&=& n・\frac{1}{\theta} - (x_1 + x_2 + \cdots, + x_n)
\end{eqnarray*}}
ここらから$\frac{\partial l(\theta)}{\partial\theta}=0$と置いて$\theta$について解きます。
{\begin{eqnarray*}
n・\frac{1}{\theta} - (x_1 + x_2 + \cdots, + x_n) &=& 0 \\
n・\frac{1}{\theta} &=& (x_1 + x_2 + \cdots, + x_n)\\
\theta &=& \frac{n}{x_1 + x_2 + \cdots, + x_n} \\
\end{eqnarray*}}
こちらで指数分布のパラメータの最尤推定量が$\frac{n}{x_1 + x_2 +\cdots,+x_n}$であることがわかりました。
この最尤推定量を具体例に当てはめて考えてみます。ある店において、お客さんが来店する間隔を5回計測してみたとします。
- 開店から1人目が来店するまでの時間:20分
- 1人目が来店してから2人目が来店するまでの時間:15分
- 2人目が来店してから3人目が来店するまでの時間:20分
- 3人目が来店してから4人目が来店するまでの時間:15分
- 4人目が来店してから5人目が来店するまでの時間:20分
来店間隔が指数分布に従うとした時、上記データから得られるパラメータ$\lambda$の最尤推定量は下記のようになります。
{\begin{eqnarray*}
\frac{5}{\frac{1}{3} + \frac{1}{4} + \frac{1}{3} + \frac{1}{4} + \frac{1}{3}}
\fallingdotseq 3.33
\\
\end{eqnarray*}}
与えられたデータから最尤推定を行うと、お客さんの来店間隔は単位時間(1時間)当たり平均$3.33$回来店されるとした時の指数分布に従うと考えられることがわかりました。
Next
指数関数について大まかに理解することができました。今後も統計関連の記事を投稿していければと思っています。