1. Introduction
競技プログラミングで度々出てくるDisjoint Setの計算量が気になったため、計算量を求めてみた。
2. Algorithm
Disjoint Setは下図のようなノードの要素が互いに素な集合（１つのノードが複数の集合に属することのない集合）を持つデータ構造である。構築は以下の操作に基づく。詳細のアルゴリズムは後述に記載する。
- make-set($n$)：各集合にノードがただ一つのみの$n$個の集合を用意
- find-root($x$)：ノード$x$のrootノードを取得→ノード$x$がどの集合に属するかを判別
- union($x, y$)：ノード$x$とノード$y$を合併
※改良によって削除に対応したアルゴリズムはこちらに記載。
3. Complexity
make-setとfind-root、unionの計算量について記述する。
3-1. Binomial tree
事前知識として二項木（Binomial tree）について述べる。二項木は以下の定義に従う。下の図をみると、次数$k$のとき深さ$k$でノードの個数は$2^{k}$個となることがわかる。
- 二項木$B_{0}$は１ノード
- 二項木$B_{k}$は一つの根（root）を持ち、二項木$B_{k-1}$、$B_{k-2}$、、、$B_{1}$、$B_{0}$までの子を持つ
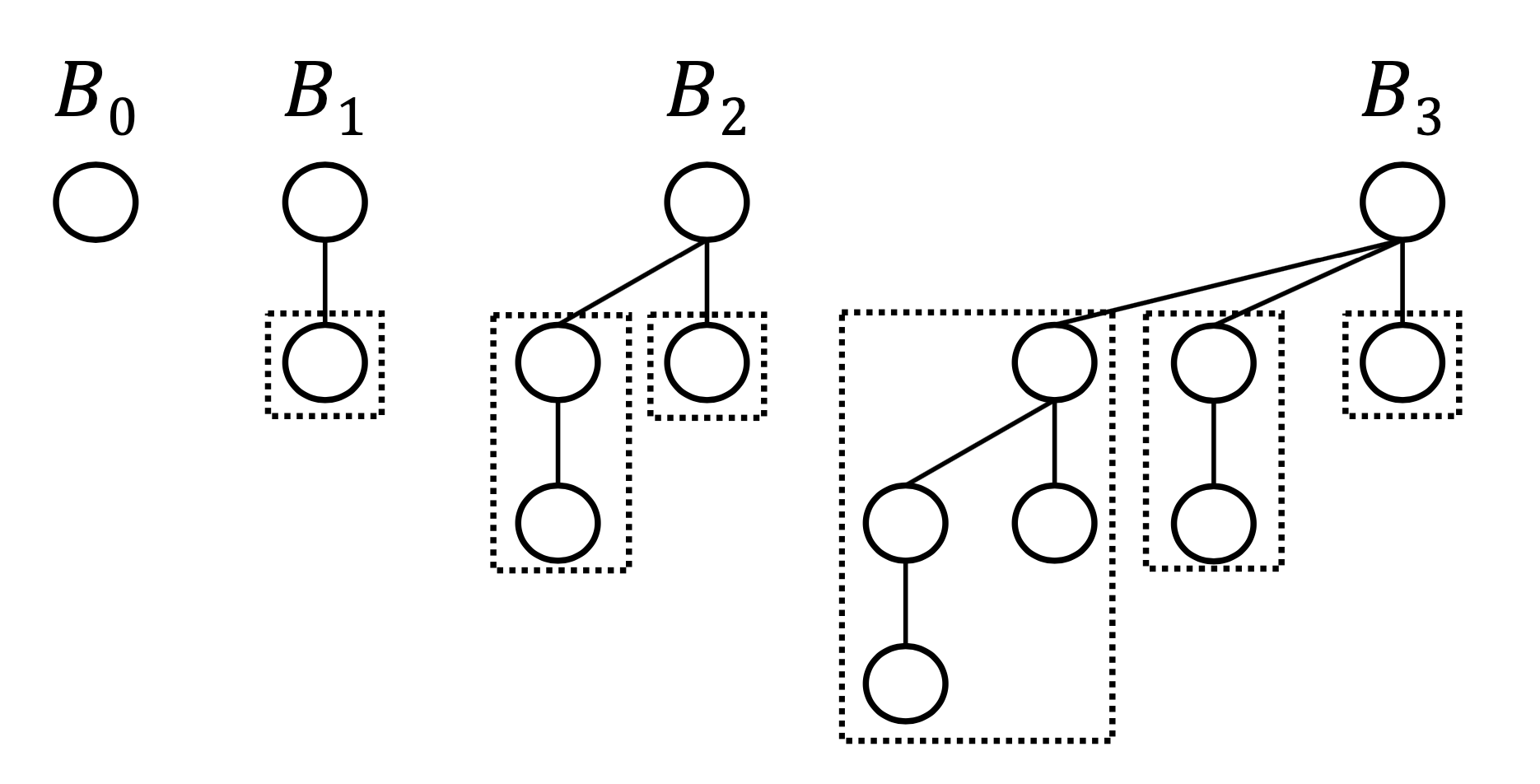また、$B_{k}(k \geq 1)$は$B_{k-1}$同士が結合した二項木で書き表せる。つまり、$B_{k}$を作るには$2^{k-1}$回、二項木を結合していけば良い。
3-2. MAKE-SET
make-set($n$)は$n$個の集合を用意し、各集合には1個ずつノードが含まれている。そして、自身のノードがrootとなるようにする。make-setの計算量は$O(n)$となる。
3-3. FIND-ROOT
find-root($x$)ではノード$x$からその木の根まで辿っていき、根にたどり着いたとき、経路圧縮（path compression）を行う。path compressionとはあるノードに対し、find-rootを行ったとき、自身を含んだ親ノード全てを根へと結合させることである（下図）。path compressionを行うことで、以降に行われるfind-root(x)を効率的に行え、find-root(x)にかかるコストを抑えることができる。
そして、ノードxに対してfind-root(x)行なった際のステップ数、つまりコストは木の深さをdとして以下となる（例：下図）。
\begin{align}
\textrm{cost(find-root(x))} = d(x) + 1
\end{align}
つぎに、各ステップで$m（n \geq m）$個分の要素についてのfind-rootのコストを考え、そのときのポテンシャルを以下のように定義する。
\begin{align}
\Phi(s) := \sum_{i=1}^m \log_{2}(d_{i}(s)+ 1) \geq 0
\end{align}
経路圧縮が行われたとき、木の深さは減少するため、ポテンシャルも減少する。つまり、次のステップで経路圧縮を行ったとき、圧縮前後で
\begin{align}
\Delta \Phi(s) = \Phi(s+1) - \Phi(s) \leq 0
\end{align}
が成り立つ。ここで、cost = 1のときのfind-rootが行われたとき、不等式の等号が成立つ。つぎに、コスト$k \geq 2$のケースを考える。加えて、find-rootによって、要素$x_{0}, x_{1}, x_{2}, \cdots ,x_{k-1}$が$x_{k}$に取り付けられたとする。
このとき、$\Delta \Phi(s)$は各要素を含んだ部分木$T_{j}\ (j=0,1,2, \cdots ,k)$としてとコスト$c$として、
\begin{align}
\Delta \Phi(s) &= \sum_{T_{j} \in T} \log_{2}(c_{T_{j}}(s+1)) - \sum_{T_{j} \in T} \log_{2}(c_{T_{j}}(s)) \\
&= \sum_{x_{j} \in x} \log_{2}(c_{x_{j}}(s+1)) - \sum_{x_{j} \in x} \log_{2}(c_{x_{j}}(s)) \\
&= 1 + \sum_{j=0}^{k-1} \log_{2}(1+1) - \sum_{j=0}^k \log_{2}(j+1) \\
&= 1 + k - \log_{2}(k+1)! \\
&\leq 1 + k \\
&\leq \alpha k \qquad (\alpha: 正の定数)
\end{align}
となる。つまり、ステップsでのコスト$k = k_{s}$として、
\begin{align}
&\Delta \Phi(s) \leq \alpha k \\
\therefore \, &k_{s} \leq -\frac{\Delta \Phi(s)}{\alpha}
\end{align}
が成り立つ。そして、$S = \{0, 1, \cdots ,\tilde{s}\}$として、ステップsまでで、n個の要素のうちのm回分のfind-rootについての全コストを考えると、
\begin{align}
\sum_{s \in S}k_{s} &\leq \frac{1}{\alpha}\sum_{s \in S}-\Delta \Phi(s) \\
&= \frac{1}{\alpha}\sum_{s=0}^{\tilde{s}}-\Delta \Phi(s) \\
&= \frac{1}{\alpha}\bigl\{\Phi(0) - \Phi(\tilde{s}) \bigr\} \\
&\leq \frac{1}{\alpha}\Phi(0) \\
&\leq \sum_{i=0}^{m-1} \log_{2}(n-i+ 1) = \log_{2}\underbrace{(n+1)(n)\cdots(n-m)} \\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \, m
\end{align}
ここで、$\Phi(0)$が最も大きくなるようなケースは以下のような、要素$x_{i}\ (i=1,2,\cdots,m)$がrootに対し、経路圧縮されずに縦に根が張っているようなケースが考えられる。
さらに、nがmに比べて十分大きいとき、m回分のfind-rootのコストの上限は
O(m\log_{2}(n))
とみなせる。したがってmake-setは$O(n)$、unionは$O(n)$であるので、ノード数$n$が十分大きいとき、Disjoint Setの作成における最悪の計算量は$O(n+m\log_{2}n)$となる。
3-4. UNION
unionの操作ではランクによる結合（union by rank）を行う。union by rankとは、2つの根付き木をunionするとき、rankの小さい方の木をもう一方の木の根の子とする方法である。rankが等しいときは２つのうちのどちらかの根付き木の子として、合併後のrankを一つ増やす。ここで、rankは経路圧縮を行っていない（find-rootを行っていない）木の高さとする。
そして、計算量を求める際に以下の補題を用いる。
$\underline{\textbf{Lemma 3.4.1}}$
ステップ$s$でのroot nodeを$u$とした、部分木$T_s(u)$のサイズ$|T_s(u)|$に対して、 ${\rm rank}(T_s(u))$は
\begin{align}
\qquad |T_s(u)| \geq 2^{{\rm rank}(T_s(u))} \cdots (1)
\end{align}
を満たす。
$\underline{\textbf{Proof 3.4.1}}$
ステップ$s$について帰納法を用いる。
初めに、$s = 0$のとき示す。$s = 0$のとき、$T_0(u) = {u}$になり、
\begin{align}
& \therefore \; |T_s(u)| = 1 \\
& \therefore \; {\rm rank}(T_s(u)) = 0
\end{align}
となるので、左辺=右辺となり、(1)を満たす。
次に、ステップ$s$のとき、(1)が成り立つと仮定して、以下の場合分けを行って、ステップ$s+1$のときに成り立つことを示す。
\begin{align}
&(i) \; {\rm rank}(T_{s+1}(u)) = {\rm rank}(T_s(u))のとき \\
&(ii) \; {\rm rank}(T_{s+1}(u)) > {\rm rank}(T_s(u))のとき
\end{align}
(i) 次のステップのときでも$rank$が変わらないケースのとき
${\rm rank}(T_{s+1}(u)) \geq {\rm rank}(T_s(u))$（$u$が${\rm rank}$の小さい部分木のとき等式）となり、
\begin{align}
& \therefore \; |T_{s+1}(u)| \geq 2^{{\rm rank}(T_s(u))} = 2^{{\rm rank}(T_{s+1}(u))}
\end{align}
ステップ$s+1$でも成り立つ。
(ii) 次のステップで${\rm rank}$が増加したケースのとき
このとき、部分木$T_s(u)$はマージされる側とする。マージする側の部分木を$T_s(v)$とする。
すると、${\rm rank}(|T_{s}(u)|) \geq {\rm rank}(|T_s(v)|)$（$u$と$v$の${\rm rank}$が等しいとき等式）が成り立ち、
\begin{align}
\therefore \; |T_{s+1}(u)| &= |T_{s}(u)| + |T_s(v)| \\
&\geq 2|T_s(v)| \\
&= 2 \cdot 2^{{\rm rank}(T_s(v))} \\
&= 2^{{\rm rank}(T_s(v)) + 1} \\
&= 2^{{\rm rank}(T_{s+1}(u))}
\end{align}
となるため、ステップ$s+1$でも成り立つ。以上より、$(i)$と$(ii)$について成り立ち、帰納法により、(1)は成り立つ。$\square$
(1)の命題を用いて、両辺の対数を取ると、
\begin{align}
&\log_{2}(|T_s(u)|) \geq {\rm rank}(T_s(u)) \\
\therefore & \; \log_{2}n \geq \log_{2}(|T_s(u)|) \geq {\rm rank}(T_s(u)) \\
\therefore & \; \log_{2}n \geq {\rm rank}(T_s(u)) \cdots (2)
\end{align}
となる。これはunion操作後において、常にrankが$\log_{2}$で抑えられることを意味している。そして、path compressionが行われていないfind-rootはrankに比例するため、find-rootまたはunionの操作での最悪の時間計算量は$O(\log_{2}n)$で、二項木のケースとなる。make-setと合わせて、$m$回unionの操作を行なったことによる、Disjoint Setの作成には$O(n + m\log_{2}n)$となる。
さらに、以下の補題により、unionによるrootノードの数は減少していく。
$\underline{\textbf{Lemma 3.4.2}}$
ステップ$s$でのroot nodeを$u$とした、部分木$T_s(u)$の${\rm rank}(T_s(u))$が$r$となるような、root nodeの集合$S(r)$を以下のように定義する。
\begin{align}
S(r) := \{ u \, | \, {\rm rank}(T_s(u)) = r\}
\end{align}
すると、全要素数$n$に対して
\begin{align}
\frac{n}{2^{r}} \geq |S(r)| \cdots (3)
\end{align}
を満たす。つまり、rankが大きくなるにつれて、root nodeの数は指数関数的に減少する項で抑えられる。したがって、rankが小さいときはroot nodeは多く、rankが大きいときはroot nodeは少ない。
$\underline{\textbf{Proof 3.4.2}}$
\begin{eqnarray}
n &\geq& \bigl| \bigcup_{v \in S(r)} T_s(v) \bigr| \\
&=& \sum_{v \in S(r)}\bigl| T_s(v) \bigr| \\
&\geq& \sum_{v \in S(r)}2^{r} \; (\,(1)により\,)\\
&=& 2^{r}\sum_{v \in S(r)} = 2^{r}\bigl| S(r) \bigr| \\
\therefore \; \frac{n}{2^{r}} &\geq& \bigl| S(r) \bigr|
\end{eqnarray}
よって、(3)が満たされる。$\square$
3-5. Iterated logarithm
find-rootによる経路圧縮とランクによる結合を行ったときの計算量を求める前の1つ目の必要な知識として、反復対数（Iterated logarithm）について述べる。$b$と$n$を正の実数として、反復対数は以下の定義に従う。
\log^{\ast}_{b}n := \left\{
\begin{array}{ll}
0 & {\rm if} \, n \leq 1 \\
1+\log^{\ast}_{b}(\log_{b}n) & {\rm if} \, n > 1
\end{array}
\right.
例えば、テトレーションの表記を用いて$b=2$として計算すると、
\begin{align}
&\log^{\ast}_{2}2 = \log^{\ast}_{2}{^{1}2} = 1 + \log^{\ast}_{2}1 = 1\\
&\log^{\ast}_{2}{^{2}2} = 1 + \log^{\ast}_{2}2 = 2 \\
&\log^{\ast}_{2}{^{3}2} = 1 + \log^{\ast}_{2}{^{2}2} = 3 \\
&\log^{\ast}_{2}{^{4}2} = 1 + \log^{\ast}_{2}{^{3}2} = 4 \\
&\log^{\ast}_{2}{^{5}2} = \log^{\ast}_{2}2^{65536} = 1 + \log^{\ast}_{2}{^{4}2} = 5 \\
& \qquad \vdots
\end{align}
となり、$\log$に比べて非常に緩やかに増加していく。また、出力値は１以下になるのに必要な最小の反復回数となっていることがわかる。より厳密には$n$が区間 $({^{y-1}b, ^{y}b}]$にあるとき、$\log_{b}^{\ast}n = y$として、反復回数は表される。そして、グラフにすると以下のようになる。横軸を$n$とし、縦軸を反復対数の値とする。プロットでは$b=2$と$\log_{2}n$の比較を行なっている。左の図が$n=10$までについて、右の図が$n=10^{7}$までのグラフとなる。
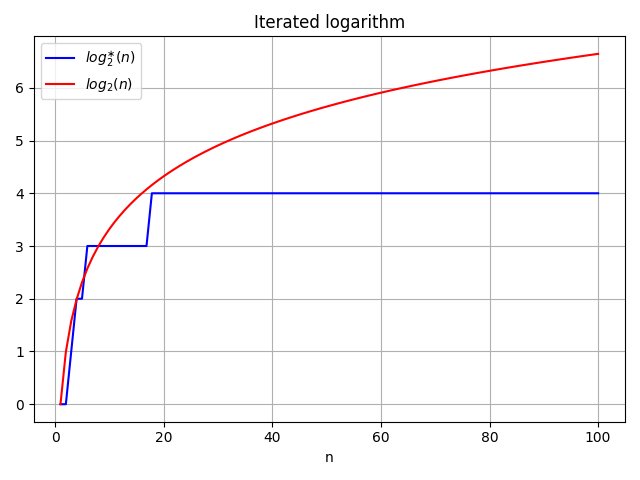
より一般的に、以下のように$\ast$表記を使って、関数$f(n)$の１以下になるのに必要な最小の反復回数を定義する。
f^{\ast}(n) := \left\{
\begin{array}{ll}
0 & {\rm if} \, n \leq 1 \\
1+f^{\ast}(f(n)) & {\rm if} \, n > 1
\end{array}
\right.
例えば、関数$f(n)$に対し、$f^{\ast}(n)$の値は以下のようになる。
| $f(n$$)$ | $f^{\ast}$$(n)$ |
|---|---|
| $n-$$1$ | $(n-$$1)^{\ast}$$=$$n-$$1$ |
| $n-$$2$ | $(n-$$2)^{\ast}$$=$$\lceil n/$$2 \rceil$ |
| $n/2$ | $(n/$$2)^{\ast}$$=$$\lceil \log_{2}$$(n) \rceil$ |
3-6. Ackermann function
find-rootによる経路圧縮とランクによる結合を行ったときの計算量を求める前の2つ目の必要な知識として、ここでアッカーマン関数（Ackermann function）について記述する。非負の整数$m$と$n$に対して、以下をアッカーマン関数$A(m,n)$の定義とする。
A(m,n) := \left\{
\begin{array}{ll}
n+1 & {\rm if} \, m = 0 \\
A(m-1,1) & {\rm if} \, n = 0 \\
A(m-1,A(m,n-1)) & {\rm otherwise}
\end{array}
\right.
$m$と$n$に値を入れていき、計算していくと
\begin{align}
A(0,n) &= n+ 1 \\
A(1,n) &= n+ 2 = 2 + (n+3) - 3 \\
A(2,n) &= 2n+3 = 2(n+3) - 3 \\
A(3,n) &= 2^{n+3} - 3 \\
A(4,n) &= \underbrace{2^{\cdot^{\cdot^{\cdot2^{4}}}}} - 3= \underbrace{2^{\cdot^{\cdot^{\cdot2^{2}}}}} - 3 = {^{n+3}2} -3\\
& \quad n+1 \qquad n+3 \\
& \vdots
\end{align}
となり、値が急激に増加していく。下図は$m=0,\cdots,4$までのアッカーマン関数のグラフで、横軸は$n$で縦軸は関数の値としている。スケールの観点上、$m=4$については$n=1$で止めている（$n=2$時点で$2^{65536}-3$ ~ $10^{19728}$、$n=3$で$2^{2^{65536}}-3$ ~ $10^{10^{19727}}$となり、expに比べ十分大きい）。
また、定義により繰り返していくと、
\begin{eqnarray}
A(m,n) &=& \underbrace{\bigl(A \circ A \circ \cdots \circ A\bigr)}(m-1, 1) =: A^{(n+1)}(m-1,1)\\
&& \qquad \; n+1
\end{eqnarray}
が成り立つ。次に$A(m,n)$の逆関数$\alpha(m,n)$について考える。非負の整数$p$と$q$とし、$n$に対しての逆関数を考えると、以下が成り立つ。
\begin{eqnarray}
p = A(m,q) \Leftrightarrow q = \alpha(m,p)
\end{eqnarray}
ここで、
\begin{eqnarray}
p = A(m,q) = A^{(q+1)}(m-1,1)
\end{eqnarray}
となるため、
\begin{eqnarray}
\alpha(m-1,p) &=& \alpha\Bigl(m-1,A^{(q+1)}(m-1, 1)\Bigr) \\
&=& A^{(q)}(m-1, 1) \\
\end{eqnarray}
となる。よって、この操作を繰り返していくと、
\begin{eqnarray}
&&\alpha^{(q+1)}(m-1, p) = 1
\end{eqnarray}
が成り立つ。これは$\alpha(m-1, p)$を$q+1$回適用すると1となることがわかる。そして、実際に$\alpha(m,p)$にどんな値が入るか計算してみと、
(i) $p\leq 1$のとき
\begin{eqnarray}
&\alpha&(m,0)=q \Leftrightarrow A(m,q) = 0 \\
&& \, \therefore A(m,q)は1以上であるため、\alpha(m,0)=0とする \\
&\alpha&(m,1)=q \Leftrightarrow A(m,q) = 1 \\
&& \, \therefore A(0,0)のとき1となるため、\alpha(m,1)=0
\end{eqnarray}
(ii) $m=0$のとき
\begin{eqnarray}
&\alpha&(0,p)=q \Leftrightarrow A(0,q) = p \\
&& \therefore \, A(0,p-1)=pより、 q=p-1\\
&& \therefore \, \alpha(0,p)=p-1
\end{eqnarray}
(iii) それ以外
\begin{eqnarray}
&\alpha&(1,p)=p-2 \\
&\alpha&(2,p)=(p+3)/2-3 \sim p/2\\
&\alpha&(3,p)=\log_{2}(p+3)-3 \sim \log_{2}p\\
&\alpha&(4,p)=\log^{\ast}_{2}(p+3)-3 \sim \log^{\ast}_{2}p\\
&& \qquad \vdots
\end{eqnarray}
となり、$m$と$p$が増加するにつれて、緩やかに増加していく関数となっていることがわかる。そして、$\alpha(m,p)$を$1$になるまでの反復回数と近似すると、
\alpha(m,p) \sim \left\{
\begin{array}{ll}
0 & {\rm if} \, p \leq 1 \\
p - 1 & {\rm if} \, m = 0 \\
p - 2 & {\rm if} \, m = 1 \\
1 + \alpha(m,\alpha(m-1,p)) & {\rm otherwise}
\end{array}
\right.
と置くことができる。
$\underline{\textbf{Proof}}$
$p \leq 1$と$m = 0, 1$は自明なので省略する。以前の結果を用いて、右辺から左辺となることを示す。
\begin{eqnarray}
&1 \, +& \alpha(m,\alpha(m-1,p)) \\
&\sim& 1 + \alpha\bigl(m,A^{(q)}(m-1,1)\bigr) \, (\because 近似した\alpha(m,p)を用いている)\\
&=& 1 + \alpha\bigl(m,A(m,q-1)\bigr) \\
&=& 1 + q-1 = q
\end{eqnarray}
ここで、$p = A(m,q) \Leftrightarrow q = \alpha(m,p)$としていたことを思い出すと、
\begin{eqnarray}
&&1 + \alpha(m,\alpha(m-1,p)) \sim q = \alpha(m,p)
\end{eqnarray}
となり、右辺から左辺が導かれる。$\square$
次に、以下のような数列を考える。
\begin{eqnarray}
\alpha(0,p), \, \alpha(1,p), \, \alpha(2,p), \, \cdots \, , \,\alpha(m,p)
\end{eqnarray}
例えば、$p=10^{4}$として計算すると
\begin{eqnarray}
10^{4}-1, \, 10^{4}-2, \, 4999, \, 11, \, 1, \, 1, \cdots
\end{eqnarray}
となり、初めは急激に減少した後、緩やかに減少していく。ここで、$\alpha(p)$を$\alpha(m,p)$が一番初めに$1$以下になるときの項目数と定義する。すると、以下のように表現でき、$p=10^{4}$のとき$\alpha(p)=4$となる。
\begin{align}
&\alpha(p) := \min\{m \, | \, \alpha(m,p) \leq 1 \} \\
&\Leftrightarrow \alpha(p) := \min\{m \, | \, p \leq A(m,1) \}
\end{align}
実際に、$p$の範囲ごとに$\alpha(p)$の値は以下のようになり、$p$が増加するにつれて緩やかに増加していることがわかる。
\alpha(p) = \left\{
\begin{array}{ll}
0 & {\rm for} \; 0 \leq p \leq 2 \\
1 & {\rm for} \; p = 3 \\
2 & {\rm for} \; 4 \leq p \leq 5 \\
3 & {\rm for} \; 6 \leq p \leq 13 \\
4 & {\rm for} \; 14 \leq p \leq 65533 \\
5 & {\rm for} \; 65534 \leq p \leq A(5,1) \sim 10^{19728} \\
\vdots
\end{array}
\right.
3-7. FIND-ROOT & UNION BY RANK
最後に、find-rootによる経路圧縮（path compression）を行った後、ランクによる結合（union by rank）を行い、２つの根付き木を合併するケースを考える。ここで、rootではないノードでかつ${\rm rank}(x) \geq 1$を満たすノード$x$について、ノード$x$の親ノードのランクがアッカーマン関数よりも大きくなるような、２つの関数を定義する。まず1つ目は、
\begin{align}
{\rm level}(x) := \max\bigl\{k \, | \, {\rm rank}({\rm parent}(x)) \geq A(k, {\rm rank}(x)) \bigr\}
\end{align}
とする。これは親ノードとのランクの差異をアッカーマン関数で表した指標となる。すると、$x$の親のrankは$x$の${\rm rank}$より少なくても1以上大きいので、
\begin{align}
{\rm rank}({\rm parent}(x)) &\geq {\rm rank}(x) + 1 \\
&= A(0,{\rm rank}(x)) \\
\therefore \; {\rm level}(x) &\geq 0
\end{align}
また、アッカーマン関数$A$は常に増加し、以下も満たされるので
\begin{align}
A(\alpha(n), {\rm rank}(x)) &\geq A(\alpha(n), 1) \\
&\geq n \\
&> {\rm rank}({\rm parent}(x)) \; (\because {\rm rank}の最大はn-1) \\
\therefore \; \alpha(n) &> \max\bigl\{k \, | \, {\rm rank}({\rm parent}(x)) \geq A(k, {\rm rank}(x))\bigr\} \\
&= {\rm level}(x) \\
\therefore \; \alpha(n) &> {\rm level}(x)
\end{align}
つまり、
\begin{align}
0 \leq {\rm level}(x) < \alpha(n) \cdots (4)
\end{align}
が満たされる。2つ目はその差異に応じた親のランクまで辿る回数を
\begin{align}
{\rm iter}(x) := \max\bigl\{i \, | \, {\rm rank}({\rm parent}(x)) \geq A^{(i)}({\rm level}(x), 1) \bigr\}
\end{align}
とする。すると、
\begin{align}
{\rm rank}({\rm parent}(x)) &\geq A({\rm level}(x), {\rm rank}(x)) \\
&\geq A({\rm level}(x),1) \\
&= A^{(1)}({\rm level}(x),1) \\
\therefore \; {\rm iter}(x) &\geq 1
\end{align}
また、
\begin{align}
A^{({\rm rank}(x) + 1)}({\rm level}(x), 1) &= A({\rm level}(x)+1, {\rm rank}(x)) \\
&> {\rm rank}({\rm parent}(x)) \\
\therefore \; {\rm rank}(x) + 1 &> {\rm iter}(x) \\
\therefore \; {\rm rank}(x) &\geq {\rm iter}(x)
\end{align}
つまり、${\rm rank}(x) \geq 1$に対し、
\begin{align}
1 \leq {\rm iter}(x) \leq {\rm rank}(x) \cdots (5)
\end{align}
が成り立つ。
続いて、ステップ$s$でのノード$x$について、あるポテンシャル$\phi_{s}(x)$を考える。$\phi_{s}(x)$は以下のように定義する。
\phi_{s}(x) \\
:= \left\{
\begin{array}{ll}
\alpha(n) \cdot {\rm rank}(x) &{\rm if} \; {\rm x \, is \, a \, root \, or} \,{\rm rank}(x) = 0 \\
(\alpha(n) - {\rm level}(x)) \cdot {\rm rank}(x) - {\rm iter}(x) &{\rm if} \; {\rm x \, is \, not \, a \, root \, and} \,{\rm rank}(x) \geq 1
\end{array}
\right.
次に$\phi_{s}(x)$の性質について述べていく。まず、$\phi_{s}(x)$の取り得る値の範囲について考える。ノード$x$がrootまたは${\rm rank}(x)=0$のとき、$\phi_{s}(x)=\alpha(n) \cdot {\rm rank}(x)$となる。$x$がrootではなくかつ${\rm rank}(x) \geq 1$のとき、(4)と(5)の結果より、下限について
\begin{align}
\phi_{s}(x) &= (\alpha(n) - {\rm level}(x)) \cdot {\rm rank}(x) - {\rm iter}(x) \\
& \geq (\alpha(n) - (\alpha(n)-1)) \cdot {\rm rank}(x) - {\rm rank}(x) \\
& = 0
\end{align}
同様に上限について、
\begin{align}
\phi_{s}(x) &\leq (\alpha(n) - 0) \cdot {\rm rank}(x) - 1 \\
& = \alpha(n) \cdot {\rm rank}(x) - 1 \\
& < \alpha(n) \cdot {\rm rank}(x)
\end{align}
が成り立つ。したがって、任意のステップ$s$において全ノード$x$に対し、$\phi_{s}(x)$の取り得る値の範囲は
\begin{align}
0 \leq \phi_{s}(x) \leq \alpha(n) \cdot {\rm rank}(x) \cdots (6)
\end{align}
となる。
これらの性質を元に、ポテンシャルの変化について以下の補題で述べる。この補題を用いて、各操作でのポテンシャルの変化から、各操作のコストを見積もっていく。
$\underline{\textbf{Lemma 3.7.1}}$
$x$はrootではないノードとする。そして、$s$回目の操作はunion by rankかfind-rootとする。すると、$s$回目の操作後の$\phi_{s}(x)$は
\begin{align}
\phi_{s}(x) \leq \phi_{s-1}(x) \cdots (7)
\end{align}
が成り立つ。さらに、${\rm rank}(x) \geq 1$かつ、$s$回目の操作で${\rm level}(x)$か${\rm iter}(x)$が変化するとき
\begin{align}
\phi_{s}(x) \leq \phi_{s-1}(x) - 1 \cdots (8)
\end{align}
が成り立つ。つまり、$x$のポテンシャル$\phi_{s}(x)$は増加しない。さらに、${\rm rank}$が正で${\rm level}(x)$か${\rm iter}(x)$が変化するとき、$x$のポテンシャル$\phi_{s}(x)$は少なくとも$1$減少する。
$\underline{\textbf{Proof 3.7.1}}$
まず、$x$はrootではないため、$s$回目の操作で${\rm rank}(x)$は変わらない。そして、make-setの初期操作から$n$は変化しないので、$\alpha(n)$も変化しない。つまり、$s$回目の操作後、$\phi_{s}(x)$の$\alpha(n) \cdot {\rm rank}(x)$の項は変化しない。${\rm rank}(x) = 0$のときでは、$\phi_{s}(x) = \phi_{s-1}(x) = 0$となり、ポテンシャルは変化しない。
続いて、${\rm rank}(x) \geq 1$を仮定する。${\rm level}(x)$は操作を重ねるごとに、変わらないか増加していくことが定義によりわかる。すると、${\rm level}(x)$と${\rm iter}(x)$の変化について、以下の$(\mathrm{i}) \sim (\mathrm{ii})$の場合分けができる。
$(\mathrm{i})$ $s$回後の操作で${\rm level}(x)$が変わらない
このとき、${\rm iter}(x)$は定義により変わらないか増加する。${\rm level}(x)$と${\rm iter}(x)$が共に変わらないとき、ポテンシャルの定義により$\phi_{s}(x) = \phi_{s-1}(x)$となる。${\rm level}(x)$が変わらず、${\rm iter}(x)$が増加するとき、${\rm iter}(x)$は少なくても$1$増加する。つまり、$\phi_{s}(x) \leq \phi_{s-1}(x)- 1$となる。
$(\mathrm{ii})$ $s$回後の操作で${\rm level}(x)$が増加する
このとき、${\rm level}(x)$は少なくても$1$増加する。すると、ポテンシャルの$(\alpha(n) - {\rm level}(x)) \cdot {\rm rank}(x)$の項は少なくても${\rm rank}(x)$減少する。また、${\rm iter}(x)$の項について、${\rm level}(x)$が増加すると${\rm iter}(x)$は小さくなるケースも考えられる。小さくなる場合、$(5)$より最大で${\rm iter}(x)$は${\rm rank}(x) - 1$減少する。よって、$s$回後の操作後の$\phi_{s}(x)$は少なくとも
\begin{align}
\phi_{s}(x) &\leq \bigl(\alpha(n) - ({\rm level}(x)+1)\bigr) \cdot {\rm rank}(x) - \bigl( {\rm iter}(x) - ({\rm rank}(x)-1)\bigr) \\
&= \phi_{s-1}(x) - 1
\end{align}
以上$(\mathrm{i})$$(\mathrm{ii})$より、補題は満たされる。$\square$
find-root
$s$回目の操作をfind-rootであるとし、その操作による経路上に$t$個のノードが含まれているとする。すると、find-rootのコストは$O(t)$となる。
そして、find-rootを行うノードを$x$とし、${\rm rank}(x)>0$とする。さらに、ノード$x$について${\rm level}(x)={\rm level}(y)$となる（親ノードとの差異が同じ）ような$x$の祖先を$y$（rootではない）があるとして、このときの${\rm level}(x)$を$k$とする。
find-rootによる経路圧縮の前では
\left\{
\begin{array}{ll}
{\rm rank}({\rm parent}(x)) &\geq A^{({\rm iter}(x))}(k,1) \\
{\rm rank}({\rm parent}(y)) &\geq A(k,{\rm rank}(y)) \\
rank(y) &\geq {\rm rank}({\rm parent}(x))
\end{array}
\right.
を満たす。すると、
\begin{align}
{\rm rank}({\rm parent}(y)) &\geq A(k,{\rm rank}(y)) \\
&\geq A(k,{\rm rank}({\rm parent}(x)) \\
&\geq A(k,A^{({\rm iter}(x))}(k,1)) \\
&= A^{({\rm iter}(x)+1)}(k,1) = A(k+1,{\rm iter}(x))
\end{align}
となる。$x$と$y$は同じ親をもつため、経路圧縮後は${\rm rank}({\rm parent}(x)) = {\rm rank}({\rm parent}(y))$となり、${\rm rank}({\rm parent}(y))$は減少しない。そして、${\rm rank}(x)$は変化しないため、経路圧縮後で
\begin{align}
{\rm rank}({\rm parent}(x)) \geq A^{({\rm iter}(x)+1)}({\rm level}(x),1) = A({\rm level}(x)+1,{\rm iter}(x))
\end{align}
となる。よって、経路圧縮により、${\rm iter}(x)$か${\rm level}(x)$の増加をもたらす場合がある。${\rm iter}(x)$が増加するとき、少なくても$1$増加する。${\rm iter}(x)$の定義と（5）より、${\rm iter}(x)$は${\rm level}(x)$が変わらないとき、${\rm rank}({\rm parent}(x))$が大きくなるにつれ、増加する。${\rm iter}(x)$が${\rm rank}(x)+1$へ達したとき、${\rm level}(x)$は$1$増加し、${\rm iter}(x)$は$1$へ戻る。例えば、下の表のようになる。
\begin{align}
A^{({\rm rank}(x)+1)}({\rm level}(x),1) = A({\rm level}(x)+1,{\rm rank}(x))
\end{align}
上記を踏まえて、${\rm rank}(x)$となるときのコストを考える。そのときのポテンシャルを$\tilde{\phi}_{s}(x)$とする。${\rm rank}(x)$となるときのコストは、だいたい${\rm rank}$が$1$のときから${\rm rank}(x)$回積み上がったものと考えられる。さらに、${\rm level}(x)$となるには、（４）より${\rm level}(x)$の取り得る値の範囲が$\alpha(n)$通りあることを考え、最大で${\rm level}(x)$が$\alpha(n)$回増加したとして、コストは
\begin{align}
\alpha(n) \cdot {\rm rank}(x)
\end{align}
に比例する。そして、コストはpathの長さに比例することから、経路圧縮によりpathは短くなるため、コストは減少すると推測できる。pathの長さ${\rm iter}$の回数に比例する。よって、${\rm iter}$が減少すると、コストが減少すると考えられる。(5)より、${\rm iter}(x)$が取りうる範囲の最大の${\rm rank}(x)$から$1$まで減少したとき、その間に${\rm level}(x) \cdot {\rm rank}(x)$分も考慮し、$\tilde{\phi}_{s}(x)$はおおよそ
\begin{align}
\tilde{\phi}_{s}(x)
\propto (\alpha(n) - {\rm level}(x)) \cdot {\rm rank}(x) - {\rm iter}(x)
\end{align}
に比例する。rootのケースや${\rm rank}=0$のケースでは、pathが変化しないことやポテンシャルは正であるため、$\tilde{\phi}_{s}(x) \propto \alpha(n) \cdot {\rm rank}(x)$となる。まとめると、
\tilde{\phi}_{s}(x) \\
\propto \left\{
\begin{array}{ll}
\alpha(n) \cdot {\rm rank}(x) &{\rm if} \; {\rm x \, is \, a \, root \, or} \,{\rm rank}(x) = 0 \\
(\alpha(n) - {\rm level}(x)) \cdot {\rm rank}(x) - {\rm iter}(x) &{\rm if} \; {\rm x \, is \, not \, a \, root \, and} \,{\rm rank}(x) \geq 1
\end{array}
\cdots (9)
\right.
となり、以降は$\tilde{\phi}_{s}(x) = \phi _{s}(x)$と置くことにする。すると、Lemma 3.7.2を思い出し、経路圧縮で${\rm level}$または${\rm iter}$が増加していくケースのとき、
\begin{align}
\tilde{\phi}_{s}(x) \leq \tilde{\phi}_{s-1}(x) - 1
\end{align}
となる。したがって、$x$のポテンシャルは少なくても$1$減少する。
続いて、ノード$x$の制約（${\rm rank}(x)>0$であり、${\rm level}(x)={\rm level}(y)$となるような祖先$y$（rootではない）が存在する）を満たす数を考える。path上にある$t$個のノードのうち、制約を満たさないケースを引いた分が、その数となる。制約を満たさないノードのケースは
- 同じレベルにはならないケース
- ${\rm rank} = 0$のケース
- rootのケース
である。同じレベルにはならないノードのケースは、鳩の巣原理と(4)より、多くとも$\alpha(n)$個ある（その個数を超えると、必ず1組は同じレベルのノードが発生）。よって、制約を満たさないケースは、他の満たさないケースを足し合わせ、多くとも$\alpha(n)+2$個となる。つまり、経路圧縮の制約を満たすケースは、少なくとも$max(0, t-(\alpha(n)+2))$個ある。find-rootを行う前のポテンシャルが$O(t)$であることを思い出すと、行った後でのポテンシャルの変化は最大で$O(t) -1 \times \bigl( t-(\alpha(n)+2) \bigr) = O(\alpha(n))$となる。したがって、$1$回のfind-rootにかかるコストは最大、つまり最悪のケースで$O(\alpha(n))$となり、$m$回では$O(m\alpha(n))$となる。
union by rank
$s$回目の操作をランクによるunionとする。union自体は$O(1)$の計算量となる。union($x, y$)の操作で$y$が$x$の親になるとする。経路圧縮時のポテンシャルについて、(9)を思い出し、$s-1$回目の操作を考える。$s-1$回目では$x$はrootとなり、$\tilde{\phi}_{s-1}(x) = \alpha(n) \cdot {\rm rank}(x)$となる。${\rm rank}(x)=0$のとき、ランク結合を行なった後もポテンシャルが変わらず、
\begin{align}
\tilde{\phi}_{s}(x) = \tilde{\phi}_{s-1}(x) = 0
\end{align}
となる。それ以外では
\begin{align}
\tilde{\phi}_{s}(x) < \alpha(n) \cdot {\rm rank}(x) = \tilde{\phi}_{s-1}(x)
\end{align}
となり、ランク結合後には$x$のポテンシャルは減少する。続いて、$y$についても考える。同じように、$s-1$回目では$y$はrootとなり、$\tilde{\phi}_{s-1}(y) = \alpha(n) \cdot {\rm rank}(y)$となる。ランク結合後、$y$のランクはそのままか、$1$増加する。そのままのときは、
\begin{align}
\tilde{\phi} _{s}(y) = \tilde{\phi} _{s-1}(y)
\end{align}
であり、$1$増加するときは
\begin{align}
\tilde{\phi} _{s}(y) &= \alpha(n) \cdot ({\rm rank}(x) + 1) \\
&= \tilde{\phi} _{s-1}(y) + \alpha(n)
\end{align}
となる。つまり、ランクによる結合で多くとも$O(\alpha(n))$のポテンシャルが変化する。よって、最大で$O(1) + O(\alpha(n)) = O(\alpha(n))$のコストがかかる。したがって、$m$回ランク結合を行なったとき、最悪で$O(m\alpha(n))$の計算量となる。
以上よりまとめると、経路圧縮 & ランク結合にかかる最悪の計算量は
\begin{align}
O(n) + O(m\alpha(n)) + O(m\alpha(n)) = O(n + m\alpha(n))
\end{align}
となる。
5. Calculation time
以下のスペックで、計算時間を求めた。
- OS：macOS Big Sur
- CPU：2 GHz クアッドコアIntel Core i5
- メモリ：16 GB 3733 MHz
横軸$n$は要素の数、縦軸は時間（sec）を表す。$m=7 \times 10^{4}$で固定して、$n$を変化させた。結果は$n$が大きくなるにつれ、処理時間は伸びる。途中の$n=7 \times 10^{7}$までほぼ同じだったが、それ以降から経路圧縮 & ランク結合を行なったときが一番処理時間が短かくなった。これは、経路圧縮 & ランク結合では無いケースでは無造作に子のノードに結合し、肥大化された集合が作成されてしまったと考えられる。
4. Conclusion
- Disjoin setの計算量を求めた
- 計算量は以下の3つの場合で求めた
- 経路圧縮：$O(n+m\log_{2}n)$
- ランク結合：$O(n+m\log_{2}n)$
- 経路圧縮 & ランク結合：$O(n + m\alpha(n))$
- $O(n + m\alpha(n)) < O(n+m\log_{2}n)$
- 経路圧縮 & ランク結合が一番計算量が小さかった
- 他の場合では肥大化された集合が作成されてしまうと考えられる
| 経路圧縮 | ランク結合 | 経路圧縮 & ランク結合 | |
|---|---|---|---|
| 時間計算量（最悪） | $O(n+m\log_{2}n)$ | $O(n+m\log_{2}n)$ | $O(n + m\alpha(n))$ |
5. Appendix
以下にPythonでの実装を記載する。
import time
import random
import matplotlib.pyplot as plt
import japanize_matplotlib
random.seed(123)
# 経路圧縮
class DisjointSet_path(object):
def __init__(self, n):
self.parents = [i for i in range(n)]
def findRoot(self,x):
if x != self.parents[x]:
self.parents[x] = self.findRoot(self.parents[x])
return self.parents[x]
def union(self,x,y):
u = self.findRoot(x)
v = self.findRoot(y)
self.parents[u] = v
# ランク結合
class DisjointSet_union(object):
def __init__(self, n):
self.parents = [i for i in range(n)]
self.rank = [0]*n
def findRoot(self,x):
return self.parents[x]
def union(self,x,y):
u = self.findRoot(x)
v = self.findRoot(y)
if self.rank[u] > self.rank[v]:
self.parents[v] = u
else:
self.parents[u] = v
if self.rank[u] == self.rank[v]:
self.rank[v] += 1
# 経路圧縮＆ランク結合
class DisjointSet(object):
def __init__(self, n):
self.parents = [i for i in range(n)]
self.rank = [0]*n
def findRoot(self,x):
if x != self.parents[x]:
self.parents[x] = self.findRoot(self.parents[x])
return self.parents[x]
def union(self,x,y):
u = self.findRoot(x)
v = self.findRoot(y)
if self.rank[u] > self.rank[v]:
self.parents[v] = u
else:
self.parents[u] = v
if self.rank[u] == self.rank[v]:
self.rank[v] += 1
def is_same_group(self, x, y):
return self.findRoot(x) == self.findRoot(y)
# aからb-1の間で、k個のランダムな整数のグループ
def rand_nodup(a, b, k):
r = set()
while len(r) < k:
r.add(random.randrange(a, b))
return list(r)
if __name__ == "__main__":
# nはノードの数、mは操作の回数
N = [7*10**n for n in range(4,9)]
m = 7*10**4
times_path = []
times_union = []
times = []
for n in N:
DS_path = DisjointSet_path(n)
DS_union = DisjointSet_union(n)
DS = DisjointSet(n)
sets = rand_nodup(0,n,m)
# 経路圧縮の時間を計測
start = time.time()
for i in range(m):
if i == m-1:
break
DS_path.union(sets[i],sets[i+1])
end = time.time() - start
times_path.append(end)
# ランク結合の時間を計測
start = time.time()
for i in range(m):
if i == m-1:
break
DS_union.union(sets[i],sets[i+1])
end = time.time() - start
times_union.append(end)
# 経路圧縮 & ランク結合の時間を計測
start = time.time()
for i in range(m):
if i == m-1:
break
DS.union(sets[i],sets[i+1])
end = time.time() - start
times.append(end)
fig, ax = plt.subplots()
# プロットするリスト
f0 = times_path
f1 = times_union
f2 = times
c0,c1,c2 = "blue","red","black" # 各プロットの色
l0,l1,l2 = r"経路圧縮",r"ランク結合",r"経路圧縮&ランク結合" # 各ラベル
ax.set_xlabel('n (個)') # x軸ラベル
ax.set_ylabel('time (sec)')
ax.set_title(r'Union find') # グラフタイトル
ax.set_xscale('log')
ax.grid() # 罫線
ax.plot(N, f0, color=c0, label=l0, marker='.')
ax.plot(N, f1, color=c1, label=l1, marker='.')
ax.plot(N, f2, color=c2, label=l2, marker='.')
ax.legend(loc=0) # 凡例
fig.tight_layout() # レイアウトの設定
plt.xticks(N, ['{:.1e}'.format(n) for n in N])
plt.savefig('union_find.png') # 画像の保存
plt.show()