この記事について
この記事は、ARISE analytics Advent Calendar 2023の23日目のために作成されました。
政治学の論文の中で、筆者が特に気に入っているものをまとめ、ざっくりと紹介します。
アドベントカレンダーの記事執筆を忘れていて、慌てて昔のネタを引っ張り出してきたわけでは決してありません。
取り上げる文献
Giilisco, M. & Montero, S. 2022. Do Major-Power Interventions Encourage the Onset of Civil Conflict? A Structural Analysis. The Journal of Politics, 84(2), pp.948-959.
はじめに
内戦は、時として悲惨な結末を生み出します。例えば、ルワンダ内戦やサラエヴォ包囲では大量殺戮がありましたし、アフガン紛争やクメール・ルージュ下のカンボジアでは人々の暮らしに根ざすものの破壊が行われました。朝鮮半島やキプロスのように、紛争によって今でも分断されている地域もあります。このような悲劇に鑑みれば、内戦を発生させないことに大きな社会的価値があります。
では、なぜ内戦は起こるのでしょうか?
伝統的には、親政府集団と反政府集団という2つのアクターに注目して内戦は研究されてきました。基本的に内戦はある特定の国・地域で起こっているものなので、これら2つの地域内集団を考えることは十分に思われます。しかしながら、内戦にはもうひとつ忘れてはならない重要な要素があります。それが外国による介入です。
もちろん、外国による介入が内戦にとって外生的なショックであれば、アクター間の相互作用を考える上でそこまで問題にならないかもしれません。しかし、ユーゴスラビア内戦では反政府集団が他国の介入を想定していたことがわかっている(Kuperman 2008)など、内戦において外国の介入が内生的であるケースは実際に存在します。ですから、反政府集団と外国政府、特に安全保障理事会の常任理事国たる大国(米・英・仏・中・露)との関係性は注目に値すると言えそうです。
反政府集団に対する大国の関わり方は、大まかに二つがあります。反政府闘争を援助するか、しないかです。前者であれば、たとえ反政府集団単体では継戦能力がなくても、援助によって内戦を継続できてしまいます。後者であれば、逆に親政府側に味方するという、反政府集団に対する強いシグナリングとして機能しそうです。ワルシャワ条約機構加盟国で内戦が起こらなかったのは、駐屯するソ連軍による介入が反政府集団に容易に予想されたからだと考えられ、これは後者の例になっています。
以上を踏まえて、今回の論文では、「内戦勃発に大国の介入が及ぼす影響は何か?」という問いに答えようとしています。
推定戦略
実証上の難点
ナイーブに考えれば、大国の介入有無を処置とし、内戦勃発有無を目的変数にすれば「効果」が推定できそうな気がします。しかしながら、問題はそう単純ではありません。以下に考えられる難点を挙げてみます。
- 標本選択:内戦は勃発した後にしか観測できない。
- 波及効果:大国は、他の大国が介入するかを伺いながら自国の介入有無を決定する。
- 複数均衡:それぞれの大国の介入有無の組が異なっていても、同一の結果になりうる。
これらの難点を乗り越えるために、今回取り上げた論文では、いわゆる因果推論ではなく、構造推定という数理モデルにデータをフィットさせるアプローチを用いています。
モデル
今回考えるのは、反政府集団と大国(米・英・仏・中・露)の関係性です。これら計6つのアクターについて、その利得$\nu$が次のように定まるとします。
\nu_i = u_i(a, w, \theta) + \varepsilon_i(a)
ただし、
- $i$:各アクター(一般化して、反政府集団$R$と大国$m = 1, 2, \ldots, M$を想定)
- $a$:各アクターの内戦に対する関与有無の組(プロファイル)
- $w$:共変量(反政府集団のもの$w^R$と介入者のもの$w^I$に分けられる)
- $\theta$:利得の係数パラメータ(知りたいやつ)
- $\varepsilon$:$\mathcal{N}(0, 1)$に従うプロファイルの特異性
と定義します。$a$を補足すると、これは各アクターの0か1をとる内戦関与有無$a_i$を集めたものなので、
a \in \{a \in \{0, 1\}^{M+1} \mid a_R = 0 \implies \forall i, a_i = 0 \}
と書けます。反政府集団が内戦を起こす気がないのであれば、大国による介入もないことに注意してください。
次に、モデルの具体的な仕様(Specification)を考えます。今回の論文では、
\begin{align*}
u_R(a, w, \theta)
&=
a_R \left[
x^R\beta + \sum_{m=1}^M a_m\left(
\gamma_m + z_m^R\gamma_0
\right)
\right], \\
u_m(a, w^I, \theta)
&=
a_m \left[
x^I\phi_m + z_m^I\chi + \sum_{m' \neq m}a_{m'}\delta_{m'm}
\right]
\end{align*}
としています。ただし、$w = (x, z)$、$\theta = (\beta, \gamma, \phi, \chi, \delta)$です。ポイントは、それぞれのアクターの利得に、別のアクターの行動$a_i$が入ってきていることで、これがアクター間の関係性(相互作用)を表現しています。また、パラメータ$\delta$が大国同士の波及効果(戦略的に補完的か、代替的か)を表現していることにも注意してください。すなわち、ある大国が介入するとき、別の大国がより介入しやすくなるのか、あるいは介入しにくくなるのかを、このパラメータによって表していると解釈することができます。
尤度
モデルがややこしいので、最尤法を用いてパラメータを推定します。ある共変量とパラメータが与えられたとき、あるプロファイルが観測される確率$\Pr(a \mid w, \theta)$がわかれば、これをデータに当てはめてパラメータを計算できます。
しかし、「実証上の難点」でも述べましたが、今回取り組んでいるケースでは複数均衡を考慮してパラメータを推定する必要があるため、$\varepsilon \sim \mathcal{N}(0, 1)$を用いてナイーブに尤度を計算することができません。そこで、詳細は割愛しますが、元論文ではある均衡の生じる確率を別途モデリングすることでこの問題を乗り越えています。また、これによりモデルが複雑化しているため、尤度はモンテカルロ計算で擬似的に計算されたもの(Simulated Likelihood)を使っています(需要推定の記事も参照)。
フィットさせるデータ
最後に、当てはめるデータについて簡単に紹介します。
- 介入のデータセット(Regan 2002)
- 1950年から1999年の、150カ国のデータ
- 大国(米・英・仏・中・露)の介入をコーディング(ロシアは旧ソ連を含む)
- 共変量のデータセット
- 国内的な特徴:地形・民主主義レベル(Polity2)・一人あたりGDP
- 国際的な特徴:同盟関係・宗主国関係・距離・国家間紛争があるか
推定結果
元論文(Giilisco & Montero 2022)から図表を引用します。
パラメータの推定結果

Table 1は、波及効果以外のパラメータの推定値です。大国の名前が書いてある行を見ると、それぞれの国が反政府集団に与える影響は、
- 正:米国
- 負:英国、フランス、中国
- わからない:ロシア
であることが示唆されています。
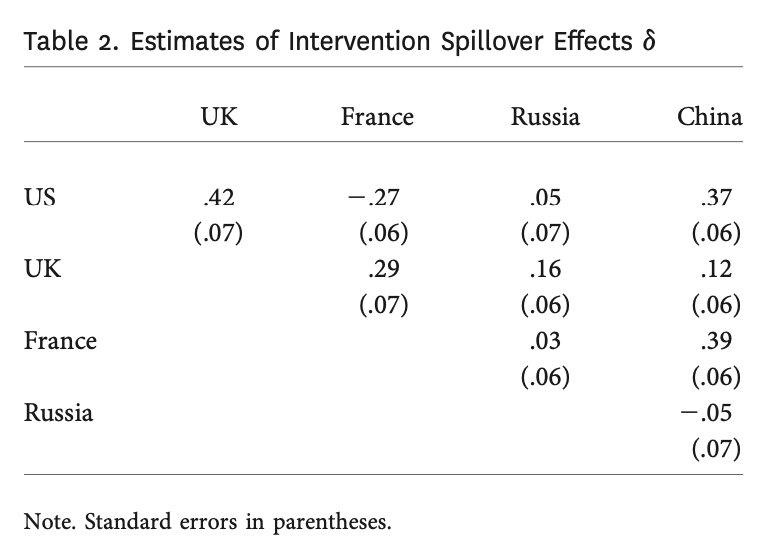
Table 2は、波及効果の推定値です。行列の国名の組み合わせがその大国間の波及効果の推定値を表しており、
- 正:米国と英国、米国と中国、英国とフランス、英国とロシア、英国と中国、フランスと中国
- 負:米国とフランス
- わからない:そのほか
となっています。これらはほとんど直観的に説明のつくものですが、米国とフランスの間の波及効果が負、すなわち両国間に戦略的な代替性があることは注目に値します。フランスの旧植民地に対する政策や、米国の介入への「ただ乗り」が関係しているものと著者たちは考えているようです。
反実仮想シミュレーション
現実のデータを使ってパラメータを推定したので、今度は逆に、モデルを真としたときにありうるデータを生成することを考えます。元論文では、特に極端な次のケースについて考察しています。
- ある大国が介入有無をアプリオリに決めるケース
- 内戦確率を最小化/最大化するために大国が協力するケース
アプリオリな介入選択
このケースでは、次の流れで意思決定が行われます。
- ある大国$m$が、あらゆる内戦への介入有無を固定する。
- つまり、この国はすべての内戦に介入する、または介入しない!
- 反政府集団と他の大国が、最適な(利得を最大化する)応答をする。
このとき、平和の確率(内戦が勃発しない確率)がどう変わるかを図示したものが以下の図です。

この図を読み解くと、米国は介入によって内戦確率を上げるが、その他の国は介入によって内戦の確率を下げることがわかります。
大国間の協力
このケースでは、次の流れで意思決定が行われます。
- 反政府集団が内戦を起こす/起こさないような介入の組が一つでもあるならば。大国はそれを実現しようとする。
- もしそのような介入の組がないならば、介入する大国の数を最大化/最小化するように行動する。
このとき、平和の確率がどう変わるかを図示したものが以下の図です。図の点線は平和の確率の実現値です、
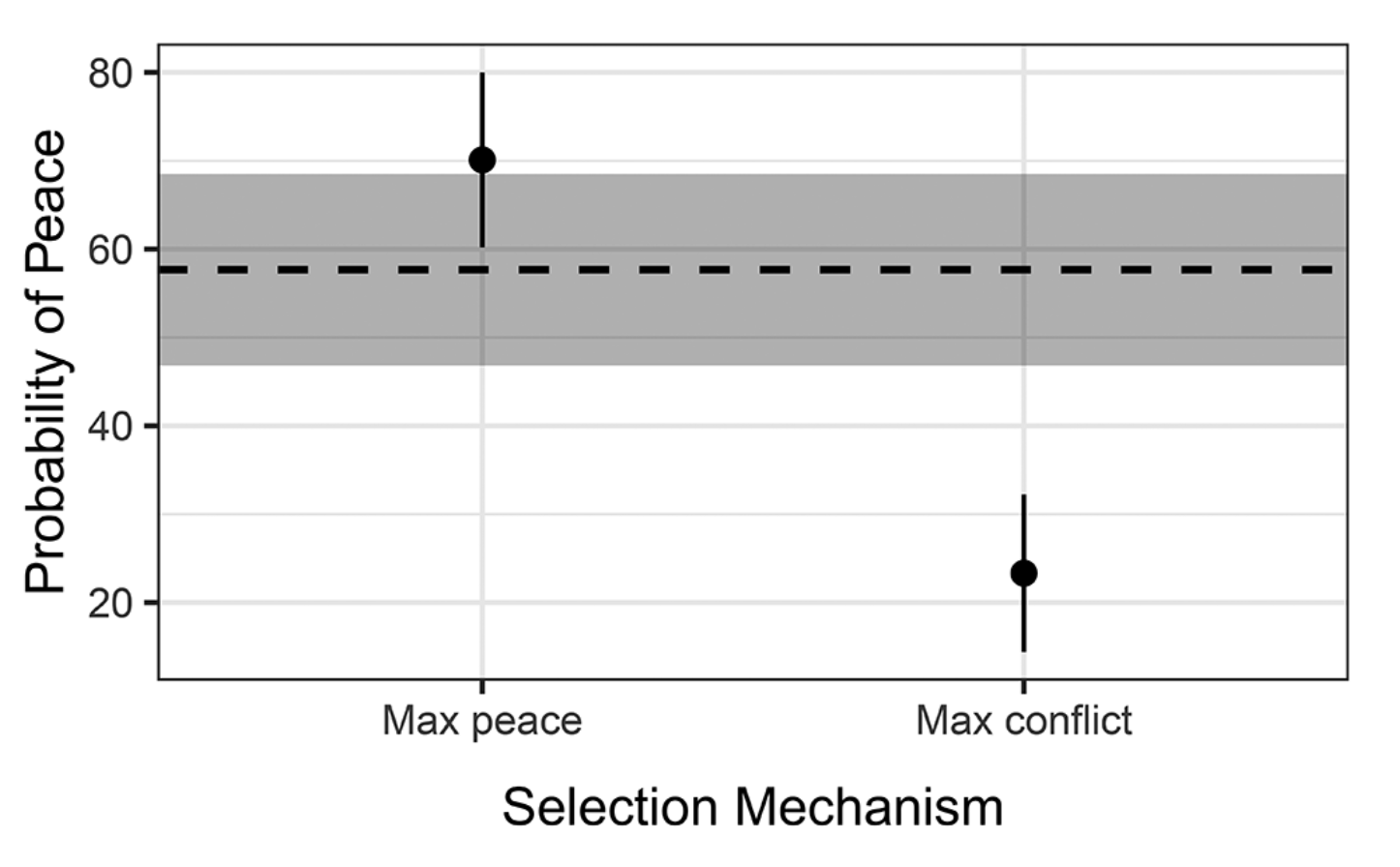
この図を読み解くと、大国間が協力することによって最善のケースが実現された場合、最悪のケースに比べて平均して40pt以上内戦が起こりにくくなることがわかります。また、実現値は最善のケースと10ptほどの差分であるため、すでに大国が実際に内戦抑止のために協力していることが示唆されました。
まとめ
結果のサマリ
- 大国の介入は内戦勃発を抑止している
- 大国同士は主に戦略的な補完性をもつ
- ある大国が介入するなら、別の大国も介入する
- 大国は内戦勃発を防ぐために実際に協力しているかもしれない
気になった点
個人的に気になったところを列挙します。
- なぜ安保理の常任理事国なのか?
常任理事国であれば糺弾されても拒否権を発動できるのは理由となり得ますが、地域大国も介入者となっている(トルコによるシリア内戦への介入など)事実があるため、いささか恣意的な気がします。
- なぜ20世紀後半(1950 - 1999)のデータなのか?
ほとんど冷戦期間だからというディフェンスがあり得ますが、国家の能力という意味では冷戦終結が1989/1991年と捉えることに疑義があります。また、人道上の罪を取り締まる国際刑事裁判所(ICC)に関するローマ規程が1998年に採択され、2002年に発効しているため、考慮するフレームを変えると結果が変わる可能性は十分あります。
主な参考文献
Giilisco, M. & Montero, S. 2022. Do Major-Power Interventions Encourage the Onset of Civil Conflict? A Structural Analysis. The Journal of Politics, 84(2), pp.948-959.
Kuperman, A. 2008. The Moral Hazard of Humanitarian Intervention: Lessons from the Balkans. International Studies Quarterly, 52(1), pp.49–80.