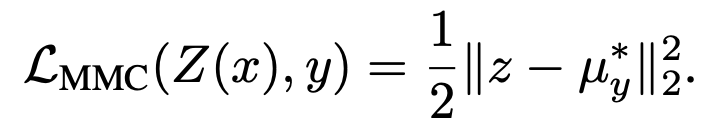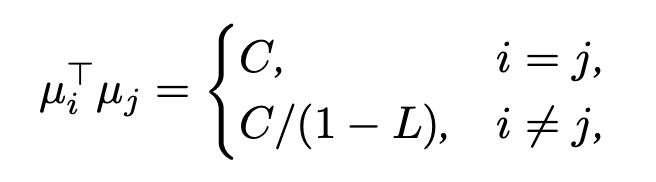"Rethinking Softmax Cross-Entropy Loss for Adversarial Robustness (ICLR2020)"の解説とPytorchによる実装

ICLR2020においてposter発表された、"Rethinking Softmax Cross-Entropy Loss for Adversarial Robustness" 1の解説と実装を行っていきたいと思います！
この論文は、著者の前の論文"Max-Mahalanobis linear discriminant analysis networks"（ICML2018) 2の進化版となっています。

pytorchによる実装はgithub[4]に載せてあります。
[4]:https://github.com/futakw/Max-Mahalanobis-CenterLoss_pytorch

論文の要旨

• 画像分類タスクにおいて用いられるCrossEntropyLossの代わりとして新たにMax-Mahalanobis Center(MMC)Lossを定義
• クラスごとにあらかじめ設計されたベクトルに特徴ベクトルが近づくように、モデルを学習させる
• 敵対的サンプル(AE:Adversarial Examples)に対するロバスト性が大幅に向上！

何がすごい？

• AEに対する脆弱性が課題とされる中、モデルのclassifierの部分（feature map以降の部分）に注目した論文は少ない
• 数学的理論に基づいて、しっかり考えられたロス関数である（数学的な分析自体がとても有益）
• 計算量はほとんど変えずに済む
• 実装が難しくない

解説

以下、論文についてざっくり解説をしていきます。

MMC Loss (Max-Mahalanobis Center Loss)とは？

まずよく用いられる、SoftmaxCrossEntropyロスは以下のように表されます。

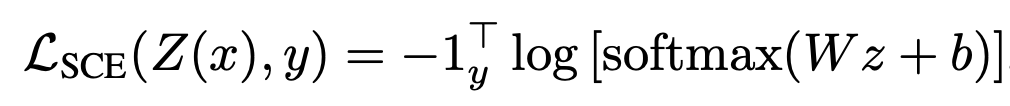
特徴ベクトルは、Linear層を通ったのちにSoftmax関数によって合計1に変更され、正解ラベルに対応する値の対数の負をとったものがロスとなります。
x,yはそれぞれinput,labelであり、z=Z(x)は特徴ベクトルです。

一方、MMCは以下のようになります。

非常にシンプルなロス関数ですね。
特徴ベクトルをいきなり、あるベクトルμと比較して二乗誤差をとっています。

ここで、あるベクトルμとは何者でしょう。

論文には、

と書いてあり、「MMDの中心ベクトル」と言っています。

このベクトルが、**「あらかじめ設計しておくベクトル」**であり、特徴ベクトルが正解ラベルに対応するベクトルμ_yに近くなるようにモデルを学習させます。

このベクトルμが、この論文のカギであり、全てです。

あらかじめ設計しておくベクトルμとは？　→　Max-Mahalanobis Distribution (MMD)

μは、「Max-Mahalanobis Distribution(MMD)の中心」とあります。

以下の画像は、クラス数L＝2,3,4の場合におけるMMDの中心位置を立体的に図示したものです。

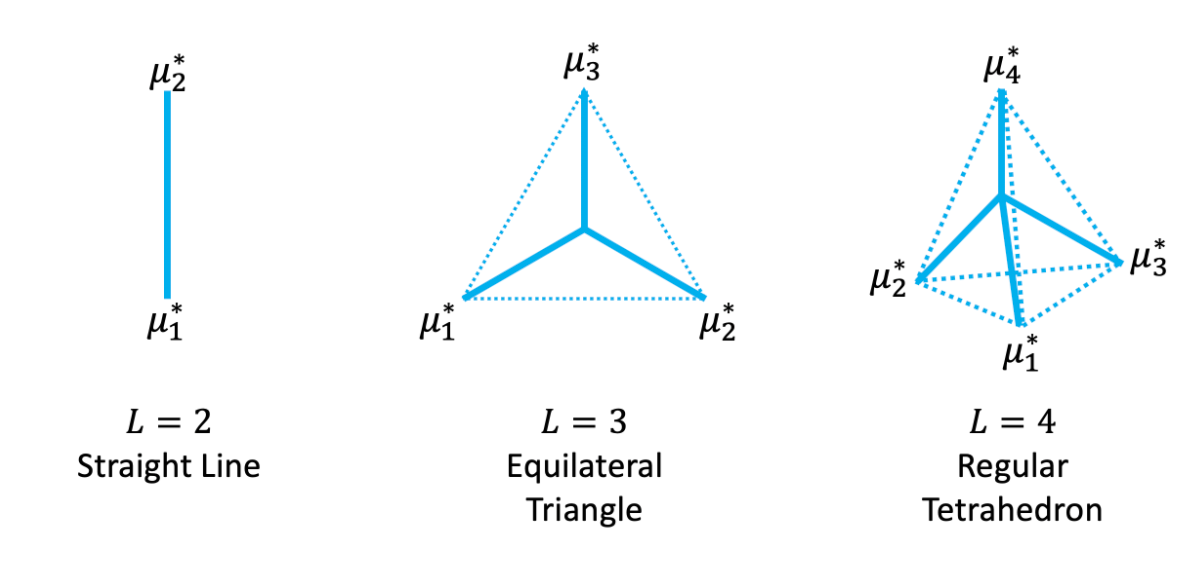
ざっくりいうと、このようにしてクラス間分布の距離がそれぞれで最大になるように特徴ベクトルを設計するのです。

Max-Mahalanobis Distribution(MMD)のざっくりとした数学的理論

ここで、数学的に説明されている理論について軽く解説していきます。

難しいので、興味がない人は読み飛ばしましょう。

＜前提＞
各クラスの分布が、混合ガウス分布になっていると仮定する。

この仮定は以下で表される。

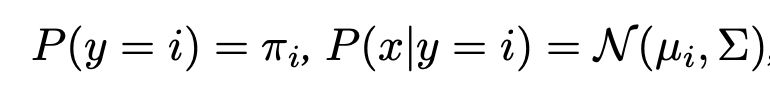
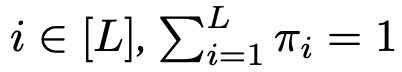であり、共分散行列Σは全クラスで共通していると仮定する。

＜目的＞
クラスごとのガウス分布のマハラノビス距離を最大化したい。

前提に基づけば、クラスi、jの分布のマハラノビス距離は以下の式によって表すことができる。

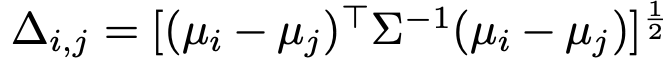
＜手法＞
クラスi,jからのサンプルxi,xjの距離の期待値を最大化する問題を解く。

まず、この問題を特に当たって問題を標準形に変換する。
共分散行列Σは、これをnonsingularだとすればコレスキー分解によって、

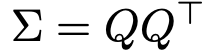
と下三角行列Qに分解することができる。このQを用いて、

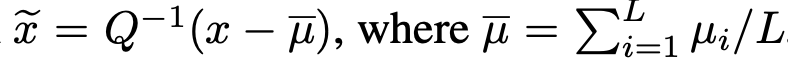
という線形変換を行うことで、問題設定は以下の標準形になる。

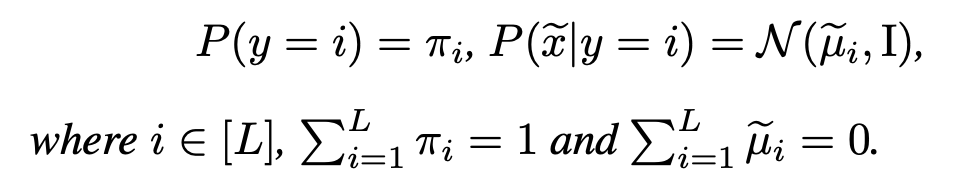
この変換では、クラス間のマハラノビス距離は不変となっている。

この設定の元で、さらにクラスi,jの出現確率πが等しいと仮定する。
このクラスi,jのマハラノビス距離の期待値は、

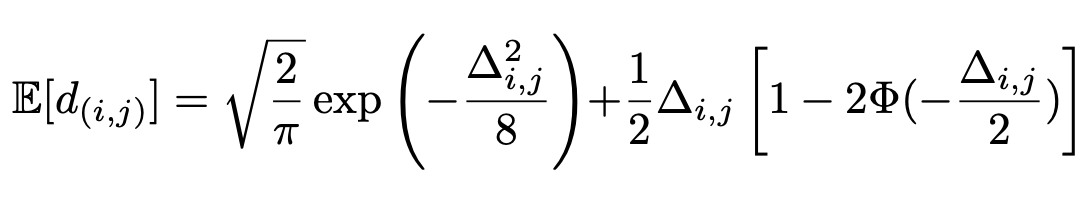
と計算できる。（証明は論文へ2）

ここで、分類器のロバストネスRBを以下のように定義した時、

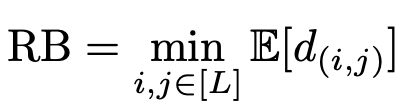
RBをどうにかして近似したRBバーは、次の上限をもつ。（証明は論文へ2）
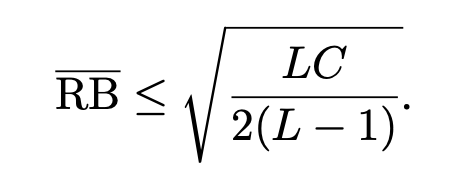（なお、 ）

そしてこの式における等号条件は、以下の式で表される。

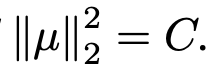＜MMDを計算する＞
等号条件を用いて、クラスごとのMMDの中心を計算する。

コレスキー分解を考える。この記事3を見るとわかりやすいかと思う。

\mu = (\mu_0, \mu_1, ... \mu_L )^T \\

を求めるに当たって、μをコレスキー分解して考えると、等号条件を用いてμを逐次的に計算していくことができる。

実装

以下、実際に実装してみたので紹介します。

MMD（＝あらかじめ設計しておくベクトル）の計算

def generate_opt_means(C, p, L): 
    """
    input
        C = constant value
        p = dimention of feature vector
        L = class number
    output
        MMD (shape=(L,p))
    """
    opt_means = np.zeros((L, p))
    opt_means[0][0] = 1
    for i in range(1,L):
        for j in range(i): 
            opt_means[i][j] = - (1/(L-1) + np.dot(opt_means[i],opt_means[j])) / opt_means[j][j]
        opt_means[i][i] = np.sqrt(1 - np.linalg.norm(opt_means[i])**2)
    for k in range(L):
        opt_means[k] = C * opt_means[k]
        
    return opt_means

ここでは、前述した数学的理論の部分より導出された式によってMMDを求めています。
実際に出てきた等号条件をコレスキー分解の式に代入してみるとわかると思います。

MM_LDAレイヤーの実装

class MM_LDA(nn.Module):
    def __init__(self, C, n_dense, class_num, device, Normalize=False):
        super().__init__()
        self.C = C #hyperparam for MMD
        self.class_num = class_num
        opt_means = generate_opt_means(C, n_dense, class_num)
        self.mean_expand = torch.tensor(opt_means).unsqueeze(0).double().to(device) # (1, num_class, num_dense)
        self.Normalize = Normalize
        
    def forward(self, x):
        b, p = x.shape # batch_size, num_dense
        L = self.class_num
        if self.Normalize: # 正規化する
            x = (x / (torch.norm(x, p=2, dim=1, keepdim=True) + 1e-10)) * self.C
            
        x_expand =  x.repeat(1,L).view(b, L, p).double() # (batch_size, num_class, num_dense)

        logits = - torch.sum((x_expand - self.mean_expand)**2, dim=2) # (batch_size, num_class)
 
        return logits

CNN層から出力されるfeature mapは、Linear層によってfeatureベクトルとなります。
そのfeatureベクトルをinputとして、それと、あらかじめ用意したMMDの「差」を計算するのがMM_LDA層です。
差は二乗誤差を計算しています。

loss計算

class dot_loss(nn.Module):
    def __init__(self):
        super(dot_loss, self).__init__()

    def forward(self, y_pred, y_true):
        y_true = F.one_hot(y_true, num_classes=y_pred.size(1)).double()
        loss = - torch.sum(y_pred * y_true, dim=1) #batch_size X 1
        return loss.mean()

MM_LDA層からの出力logitsは、(batch_size, num_class)の形をしています。
その出力のうち、正解ラベルに該当する値をLossとして取ります。

したがって例えば、ミニバッチのうちの1つ目のデータのラベルが5、2つ目のデータのラベルが3の場合は、

Loss = logits[0][5] + logits[1][3] + ...

となります。

ここでMM_LDA層からの出力(logits)はMMDとの近さを表すので、**「特徴ベクトルが、正解ラベルのMMDに近くなるように」**Lossをとっているということです。

実験

今回、実際にAEに対してロバストになるか簡単な実験しました。

比較内容

ベースモデル：ResNet34
比較分類器：SoftmaxCrossEntropy(SCE)Loss, MMC
比較攻撃手法：なし, PGD, FGSM

SoftmaxCrossEntropy(SCE)Lossは従来のクロスエントロピーロスによる分類を指し、
MMCが本論文1で2020に提案された、論文2の修正版です。

敵対的サンプルAEの生成方法として、PGD,FGSMを試しました。

結果

モデル	Clean	PGD	FGSM
SCE	86.54	41.85	14.21
MMC	80.68	43.10	26.61

単位はパーセント[%]です。
論文で用いられたハイパーパラメータが全てはわからなかったので論文とは正確な数値は異なりますが、ロバスト性が向上していることがわかります！

複雑な実装をせずに、精度が向上しているという結果は非常に喜ばしい結果と言えます。

（ただし論文中ではSCEとMMCのCleanでの精度をほぼ同じにして比較しているため、正確な値ではありません。）

終わり

ここまで読んでいただきありがとうございました！

理論を完全に理解できたわけでもなく、また実装においてミスがあるかもしれませんが、参考になれば幸いです。