UnityでiOSのジャイロの使い方をちゃんと説明する

UnityでiOSのジャイロ使おうと思って調べたところ、
「Input.gyro.attitudeでQuatenionで取れまっせ」ってのは出てくるんだけど
ちゃんと座標系について説明してるところが見つけられなかったので
ふにゃふにゃ書いてみる

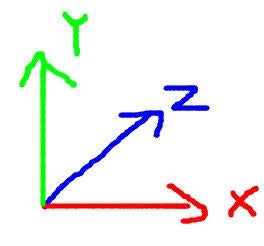
#座標系の違い

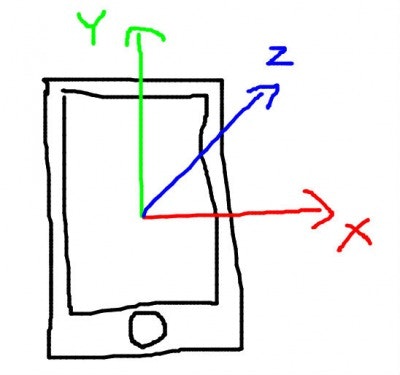
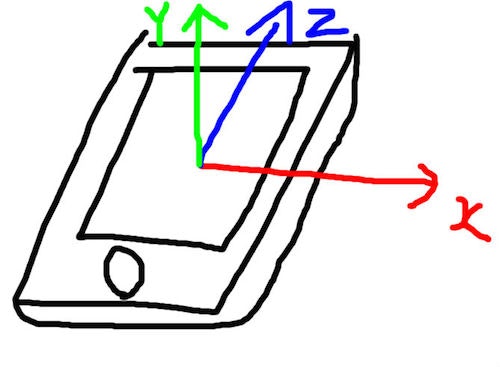
iOSの座標系はiPhoneだとこう
（ Screen.orientation == ScreenOrientation.Portrait の場合。Screen.orientationの値によってかわるので注意）

Unityはお馴染みのこれ

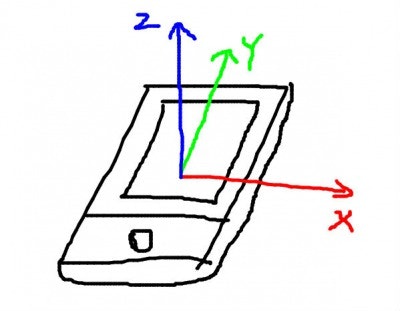
注目ポイントは２点

• 座標系が右手系と左手系
• 無回転な標準状態がiPhoneを置いた状態。Y軸ではなくZ軸が重力の反対方向

#座標系の変換

今回はiOSのカメラが向いている方向をUnity上のZ軸として扱いたかったので
こういう変換を行いたい

→

##右手系左手系

iOSは右手系、Unityは左手系なので変換が必要
なのだけど、ここなんとなくやっててちゃんと説明してるとこあんまなかった

大事なのは 右手系→左手系の変換は一律決まった操作ではない ってこと

Quaternionの右手系左手系変換でよりわかりやすいのはXYZのどれか一軸を正負反転させる
どの軸を反転させるかは用途に応じて自分で決める必要がある

今回はZ軸を反転させる

が、今回は無回転状態を揃えるためにY軸とZ軸を入れ替える操作を行う

##Quaternionで変換

Quaternionの定義は

$回転軸V(n_x,n_y,n_z)まわりにθ度の回転を、$

$Q(x,y,z,w)$
$x=n_xsin(θ/2)$
$y=n_ysin(θ/2)$
$z=n_z*sin(θ/2)$
$w=cos(θ/2)$

$と表したもの$

なので、 YZ軸入れ替えはq.y と q.zを入れ替える

・・・だけではなく、

右手系と左手系では軸周りの回転方向も反対になるので θ*=-1f な操作も必要
これはsin()にしか影響ないので、

YZ軸入れ替えは

var q = Input.gyro.attitude;
var newQ = new Quaternion(-q.x, -q.z, -q.y, q.w);

となる

これで座標系揃った！

#無回転状態をあわせる

上記変換で以下のようになった
→

まだカメラの向き＝Z軸という無回転状態にできていない
これはUnity上で無回転のときにZ軸が下を向くように先にX軸回転しとけばよい
transformの親子関係でやっちゃってもいいけど、このために空のGameObjectを置いとくのもアレなので、
計算で求めちゃう

q *= Quaternion.Euler(90f, 0f, 0f);

これで出来た！

まとめると

var rotRH = Input.gyro.attitude;
var rot = new Quaternion(-rotRH.x, -rotRH.z, -rotRH.y, rotRH.w) * Quaternion.Euler(90f, 0f, 0f);

transform.localRotation = rot;

こんな感じでiOS端末の向きに追従するGameObjectができる！