NIPS 2018に採択された論文 Embedding Logical Queries on Knowledge Graphの解説をしつつ、この論文で提唱された新しい手法が、今後の人工知能・機械学習の世界にどのような影響をもたらすかを、今回記事と次回記事(12月25日公開予定)の2記事で、自分なりの解釈を交え解説してみます。今回は、前半として本論文の解説をしようと思います。
この記事は、研究者はもちろん、機械学習の初学者も含めた人を対象にしており、難しいことはなるべく平易な表現にし、わかりやすくなるようにお伝えしようと思います。
これはどんな論文なのか
一言で言うと、グラフで表されたデータ上における隠れたエッジ(関係性)を見つけるため、 グラフ自体を低次元空間上に埋め込み、論理演算をその空間上の幾何操作に置き換えることで、いままで時間のかかっていた探索を線形時間で達成することができた 、というものです。
グラフで表されたデータとはどんなものがあるのでしょうか。論文中では、下記のものが紹介されています。
「病気 $d_1$ と 病気 $d_2$ が結びついている(assoc)タンパク質が対象としている(target)薬物 $c_?$ を予測せよ」
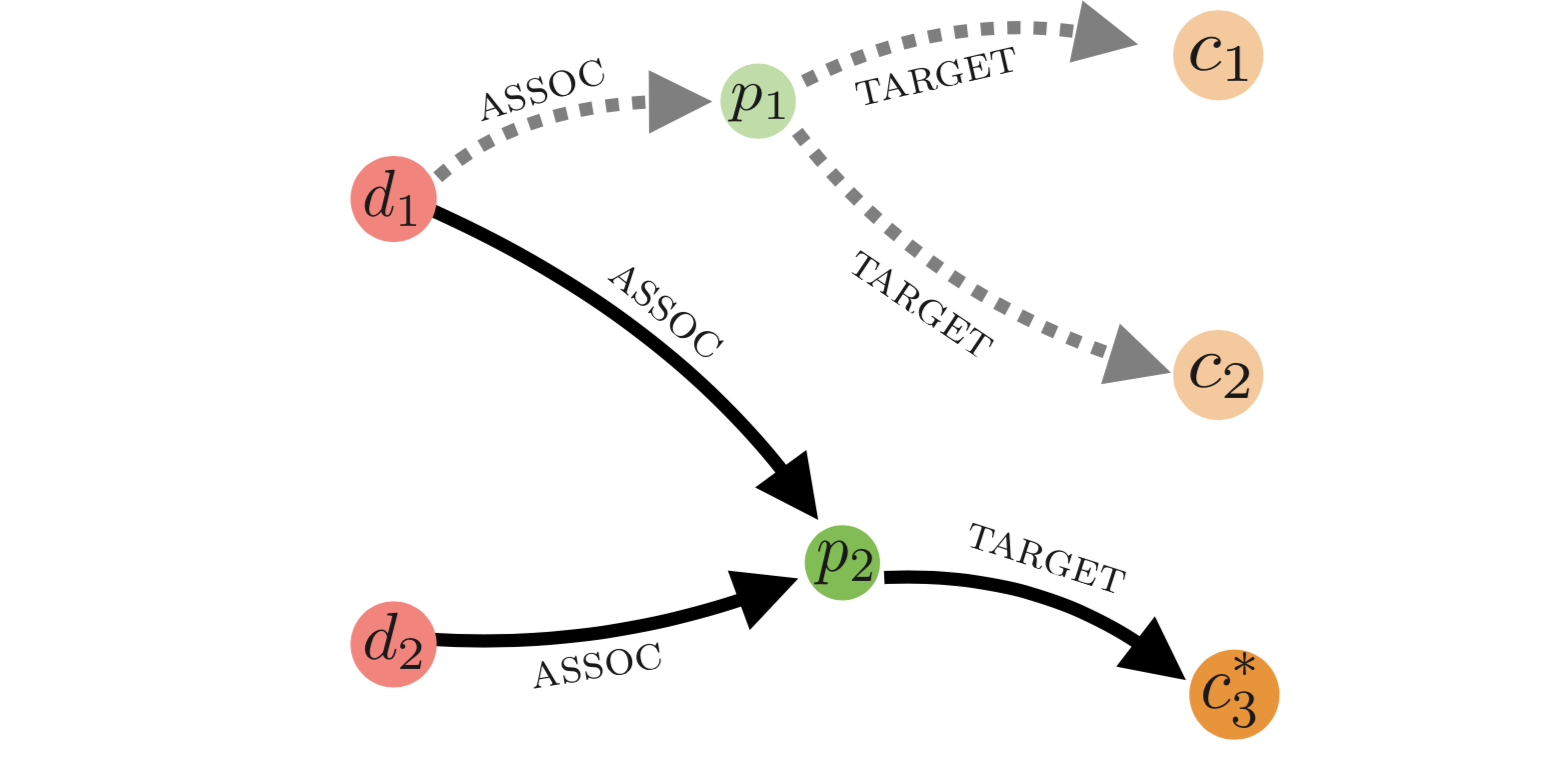
これは、すでに知られている薬物・病気・タンパク質とその間で起こる作用についてのナレッジベース上でのクエリの例です。病気やタンパク質がノード(頂点)で、assocやtargetという関係性がエッジ(枝)として表されています。
他にも、ソーシャル口コミサイトのRedditにおいて、
「ユーザー $u$ が 賛成票を投じる(upvote)ポストが所属(belong)しているコミュニティ $c_?$ を予測せよ」
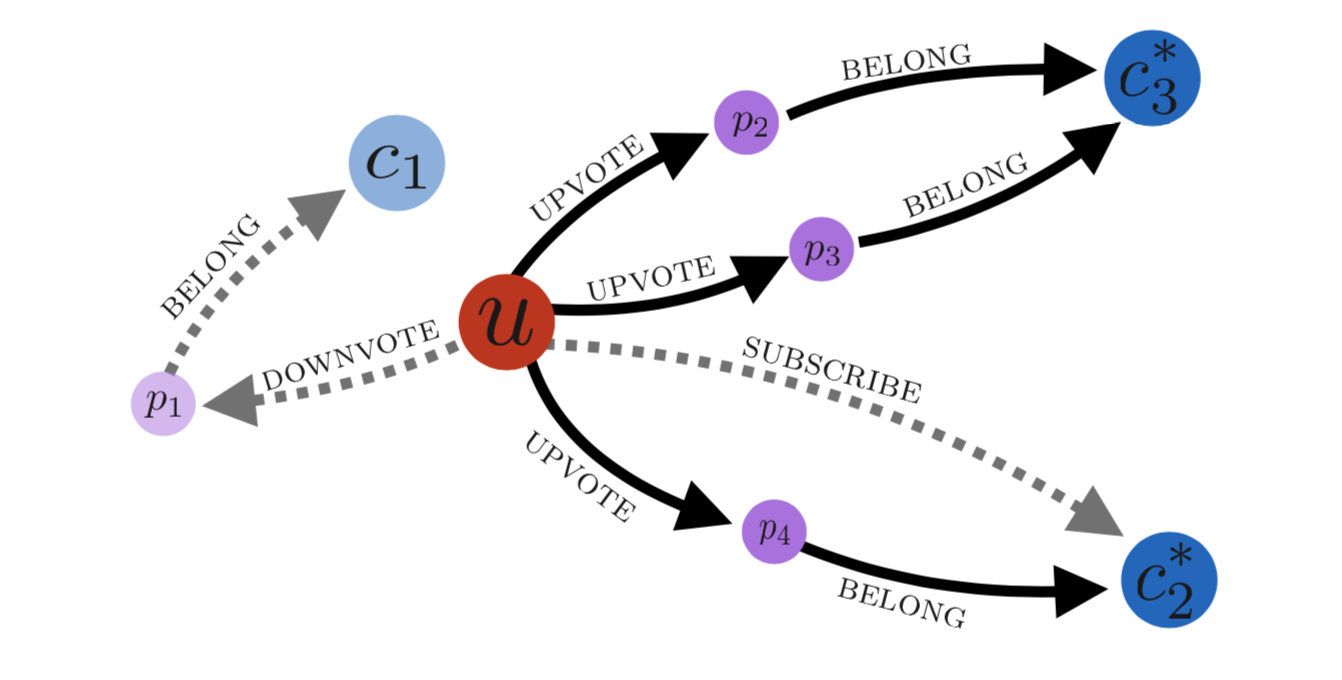
といったクエリの例もあります。
上図における点線はナレッジベース上に存在するエッジ(グラフの枝)、実線は、クエリの答えとなるサブグラフ(グラフの一部分)となります。
これらのクエリは、Conjunctive Queryと呼ばれています。 Conjunctive Queryとは、 論理積($\land$)と 存在量化子(∃)オペレーターだけ使ったクエリのことで、上の例のそれぞれのクエリを表すと、下記のようになります。つまり、これらのクエリは、「◯◯と、△△と、□□をすべて満たすXは存在するか?」を調べるクエリということです。


この問題の難しいところは、元となっているナレッジベースは不完全で、現実には存在しているのに観測されていないエッジ(関係性)があるということを前提としています。そのため、「エッジは存在していないがおそらくここにはエッジが存在している可能性が高い」ということを予測します。
この場合、すべてのふたつの頂点の組み合わせに対してエッジが存在する可能性があるので、すべての2組の頂点に対してエッジの存在確率を計算しなければならず、これは大変な計算時間のかかるものでした。この論文に書かれている手法は、その計算時間を大幅に短縮しています。
提案手法の仕組み
主なメカニズム
先程の、このクエリを例にとって、提案手法を解説してみます。このクエリは、 「病気 $d_1$ と 病気 $d_2$ が結びついている(assoc)タンパク質が対象としている(target)薬物 $c_?$ を予測せよ」 というものでした。

提案手法の大きなステップは以下のとおりです。
1. クエリをグラフで表す
クエリを、DAG(Directed Acyclic Graph, 有向非巡回グラフ)で表現します。つまり、Conjunctive Queryの形をしているものを、上記のようなグラフ図で表現するということ。
2. アンカーノードの埋め込み表現を求める
クエリ中で出発点となるノード(アンカーノード)、ここでは $d_1$ と $d_2$ を、低次元空間に埋め込みます。つまり、これらのノードの埋め込み表現(ベクトル表現)それぞれ${\bf z_1}$と${\bf z_2}$を求めます。
3. Projectionの適用
アンカーノードの埋め込み表現に対し、Projection $\mathcal{P}$ を適用します。 $\mathcal{P}$は、グラフの枝(関係性)にあたる幾何操作で、ここではassocの操作にあたる幾何操作を${\bf z_1}$と${\bf z_2}$に適用します。 $\mathcal{P}$ は、行列${\bf R}_\tau$ を意味します。 $\tau$ は、assocといったエッジタイプを表します。
4. Intersectionの適用
上記の操作で得られた複数のベクトルに対して、Intersection $\mathcal{I}$ を適用します。$\mathcal{I}$は、論理積($\land$)を意味する操作で、複数のベクトルをとってひとつのベクトル表現を返します。
5. さらにProjectionを適用
3~4を繰り返します。ここでは、$\mathcal{I}$によって得られたベクトルにさらにtargetというエッジにあたる$\mathcal{P}$を適用します。
6. スコア計算
最終的にこの操作で得られたベクトル${\bf q}$が、クエリを満たすノードの埋め込み表現になります。この ${\bf q}$と他のすべてのノード $v$ の埋め込み表現${\bf z}_v$とのスコアを以下の式で計算します。
{\rm score}({\bf q} ,{\bf z}_v) = \frac{{\bf q} \cdot {\bf z}_v}{||{\bf q}||\, ||{\bf z}||_v}
このスコアは一種の距離を表しており、ここからのk近傍法で${\bf q}$と一番近いものを求めます。これで、正解ノードを求めることができます。
言葉で説明するとわかりにくいですが、下図の右側の図がすべてを物語っています。
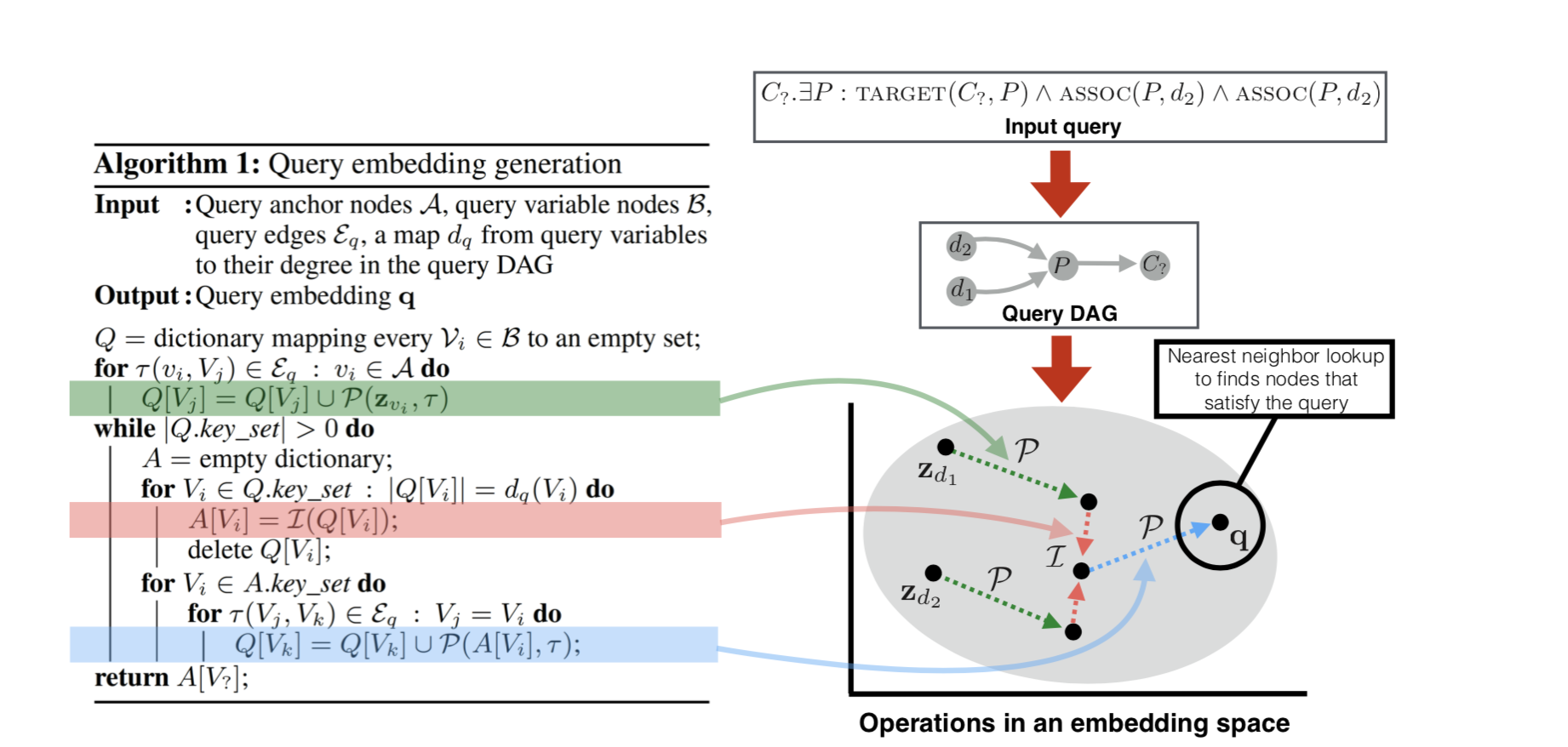
つまり、論理積($\land$)をIntersection $\mathcal{I}$に、関係性をProjection $\mathcal{P}$に置き換え、出発点のノードに適応してたどりついた先をクエリの表す点とみなすという方法です。
どうやって学習するの?
次に、これらのグラフのノードをどうやって埋め込み表現にするか、$\mathcal{P}$や$\mathcal{I}$を表す行列をどのように求めるかを解説します。
まず、グラフのノードをどのようにして低次元空間上に埋め込むかですが、この論文中には詳しく書かれておらず、Embed all the things!という論文のbag of featuresという手法を用いたと書いてあります。
ノードタイプが$\gamma$であるすべてのノード${\bf z}_u$は、 ${\bf x}_u \in \mathbb{Z}^{m_r}$ という対応する二値ベクトルをもち、それを用いて、
{\bf z}_u = \frac{{\bf Z}_\gamma{\bf x}_u}{|{\bf x}_u|}
と表すことができます。${\bf Z}_\gamma$という行列を学習するイメージです。 ${\bf x}_u$ は、例えば、Redditのレコメンドデータベースの投稿の例においては、$投稿内の単語の出現を0-1で表したベクトルを用いるようです。
次の$\mathcal{P}$や$\mathcal{I}$の前にノーテーションの確認ですが、$[[q]]$ は、クエリ$q$の真の正解集合を表します。学習データにおいては、 $[[q]]$は完全には観測されていない場合もあります。それと区別して、学習データ内での正解集合を、$[[q]]_{train}$と表します。ゴールは、下記を満たすようなクエリ(の答え)の埋め込み表現 ${\bf q}$を求めることです。
{\rm score}({\bf q} ,{\bf z}_v) = 1, \forall v \in [[q]]
\\
{\rm score}({\bf q} ,{\bf z}_v) = 0, \forall v \notin [[q]]
$\mathcal{P}$や$\mathcal{I}$やノードの埋め込みに関しては、すべて確率的勾配降下法(Stochastic Gradient Descent, SGD)で学習することができ、その際の損失関数は以下で表されます。
\mathcal{L}(q) = \max(0,1 - {\rm score}({\bf q}, {\bf z}_{v^*}), + {\rm score}({\bf q}, {\bf z}_{v_N}))
$v^*$は正例で、$v_N$は負例。つまり、
v^* \in [[q]]_{train} \\
v_N \notin [[q]]_{train}
$\mathcal{I}$は、下記の式のような形で実装された。
\mathcal{I}(\{{\bf q}_1, \cdots ,{\bf q}_n \}) = {\bf W}_\gamma\Psi(NN_k({\bf q}_i), \forall i = 1, \cdots, n)
${\bf W}_\gamma$ は各ノードタイプ $\gamma$について訓練可能な遷移行列で、$\Psi$はベクトルの平均や、最小値を返すベクトル関数、 $NN_k$ は $k$ 層のニューラルネットワークを表す。
$\mathcal{P}$に関しては
\mathcal{P}({\bf q}, \tau) = {\bf R}_\tau{\bf q}
と表される ${\bf R}_\tau$ を求めることがゴールで、これは ${\bf q}$に所属するノード $v$へとタイプ $\tau$のエッジ経由でつながるノードの集合を表します。パスとエッジのエンコーディングに関してのこれ以上の詳しい説明は、は、それぞれIEEE,ICMLで採択された A review of relational machine learning for knowledge graphsやA three-way model for collective learning on multi-relational dataを参照とのことです。
次回は、この論文で提案された手法および同じような手法が、今後の人工知能の世界にどのようなブレイクスルーを起こすかについて書きます。