はじめに
本記事は、MATLABのライブエディターで作成した文書をQiita投稿用に移植しています。
なお、元となるライブエディターファイルはgithubで公開しています。
背景
GMRES法(一般化最小残差法、Generalized Minimal RESidual method)を理解したい。理論面の解説記事は多数あるが、実装例はソースコードがポンとアップされているだけでコメントもない。。。。
→実装例を公開しよう。
目的
解説論文[1]とその解説記事[2]に対して、本記事ではMATLABでの実装を紹介する。具体的には、3元1次連立方程式にGMRES法を適用することで理解を補助する。
問題設定
例題として次の連立方程式を考える
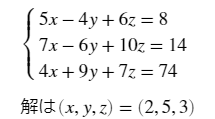
GMRES法では連立方程式をAx=bと行列で表現する。
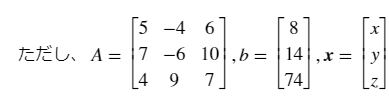
GMRES法のアルゴリズム
詳細な原理は参考文献[1],[2]に譲るため、ここではアルゴリズムのみを再掲する。
なお、各アルゴリズムの行番号を小見出しとして記載している。
GMRESのアルゴリズム
実装
GMRES-L1.
Choose a vecotr $x_0$
初期解を設定する。
正答以外ならば任意の値でよい。
x0 = [0 0 0]'
GMRES-L2.
Compute $r_0 =b-{\mathrm{Ax}}_0 ,v_1 =r_0 /\left|\right|r_0 \left|{\left|\right.}_2 \right.$
初期残差を計算する
ここで$\Vert r_0 \Vert$は、ベクトルのノルムを表す。
r0 = b - A*x0
1つ目の基底ベクトルの計算はArnoldi法-L1にて実施。
GMRES-L3.
Apply Arnoldi process to A to obtain $V_m$
Arnoldi法
変数$V_m$をクリロフ部分空間の基底ベクトルの集合体とする。
基底ベクトル$v_i \in R^{3\times 1}$、$V_m =\left\lbrack \begin{array}{cccc}
v_1 & v_2 & \cdots ; & v_m
\end{array}\right\rbrack$として実装する。
Arnoldi法-L1.
Choose a vecotr $v_1$
初期残差ベクトルを正規化した結果を1つ目の基底ベクトルとする
Vm(:,1) = r0 ./ norm(r0)%1つ目の基底ベクトル
Arnoldi法-L2.
for j=1 to m do
繰り返し回数mは、行列Aのサイズ(=変数の数)となる。
※発展的には、m回以下の繰り返しであっても解の精度が十分になった時点で打ち切る方法もあるようです。
m = length(A);
Hm_ = zeros(3,3);
for j=1:m
Arnoldi法-L3
$h_{i,j} =\left({\textrm{Av}}_j ,v_i \right);\left(i=1,\ldotp \ldotp \ldotp ,j\right)$
for i=1:j
Hm_(i,j)=(A*Vm(:,j))'*Vm(:,i);
end
Arnoldi法-L4
$\hat{v_{j+1} } =Av_j -\sum_{i=1}^j h_{i,j} v_i$
vec_hat = 0;
for i = 1:j
vec_hat = vec_hat + Hm_(i,j).*Vm(:,i);
end
v_hat = A*Vm(:,j) - vec_hat;
Arnoldi法-L5
$h_{j+1,j} =\Vert \hat{v_{j+1} }\Vert_2$
Hm_(j+1,j) = norm(v_hat);
Arnoldi法-L6
$v_{j+1} =\frac{\hat{v_{j+1}}}{h_{j+1,j}}$
Vm(:,j+1) = v_hat ./ Hm_(j+1,j);
Arnoldi法-L7
end for
end
GMRES-L4
Find $y_m$ which minimizes $\Vert \Vert r_0 \Vert_2 e_1 -\bar{H_m}y\Vert_2$
GIVENS回転による上三角行列化
$\bar{H_m }$を上三角行列に変換するためには、Givens回転をm回すればよい。
下ではOmega{i}はi番目のGivens回転の行列を表し、Omega{i}$\in R^{4\times ;4}$
m = length(Hm_)-1; %Givens回転する回数
for i=1:m
%[1]-式(36)
nu = sqrt(Hm_(i,i)^2 + Hm_(i+1,i)^2);
c_i = Hm_(i,i)/nu;
s_i = Hm_(i+1,i)/nu;
Omega{i} = diag(ones(m+1,1));
Omega{i}(i:i+1,i:i+1) = [c_i,s_i
-s_i,c_i];
Hm_ = Omega{i} * Hm_;
end
Rm_ = Hm_; %この時点でHm_はGivens回転後の上三角行列なことは注意
式(48)を解く
$g_{m;} -R_m y=0\cdots \left(48\right)$を解く
$\bar{g_m } =Q_m |r_0 {|}_2 e_1$を計算する。
[1]の(43),(44)式に従ってもいいが、基本を理解するために愚直に計算する。
まず、単位ベクトル$e_1$を設定する
e1 = [1 0 0 0]'
gm_ = norm(r0)*e1;
for i=1:length(Omega)
gm_ = Omega{i}*gm_;
end
掃き出し法での求解
上三角行列なので、一番下から上に向かって順番に解を確定していけばよい。
ただし、$\bar{R_m } ;,\bar{g_m }$はそれぞれ一番下の行が0(計算誤差で0にならないが)であるため、
1個上(length(Rm_)-1)から計算する。
[1]-式(47)のあたりの計算に相当する。
min_y = zeros(length(Rm_)-1,1); %解の格納先
for i=length(Rm_)-1 :-1:1
min_y(i) = (gm_(i) - Rm_(i,:) * min_y)/Rm_(i,i);
end
GMRES-L5
Compute $x_m =x_0 +V_m y_m$
元の方程式の解を求める
x0 + Vm(:,1:m)*min_y
おわりに
MATLABのライブエディターで一式書き上げ、その結果を投稿しました。
一発で変換できればいいのに・・・二度と変換作業したくないですが、
かといって、ライブエディターのデータだけupする場所があるわけでもなく。。。

