SILS環境の構築のためのDCモータのパラメタ同定及び制御実験入門

緒言

　本書の対象とする読者の能力として，Arduino等を含めた一般にマイコンと呼ばれるような組込開発が行えることである．また，MATLAB及びSimulinkを使用するため、それらを使用できる環境が望ましい．

目的

　DCギヤードモータの印加電圧を制御することにより出力軸の角度制御を実現することである．そのために，システム同定を行い実機における制御結果とシミュレーション結果の比較する．その後，Software In the Loop Simulation(以下SILS)用の環境構築までを一通り行うことである．

ハードウェア概要

システムの構成

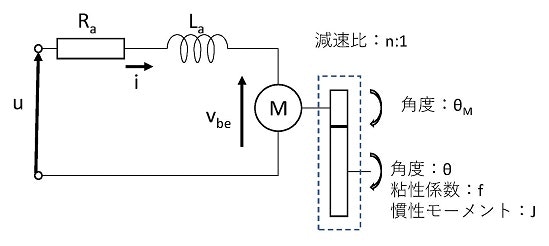
　本書で制御対象とするDCモータシステムを図1に示す．本システムはエンコーダ付きDCギヤードモータ，減速用歯車，モータドライバ及びRX631マイコンによって構成される．また，各ハードウェアの仕様を表1に示す．仕様からわかるように，DCモータ出力は最終的に$950:12$に減速される．また，エンコーダはモータの軸に取り付けられており，出力軸に対するエンコーダパルス数は，$512\times\frac{950}{12}[pulse/回転]$となる．

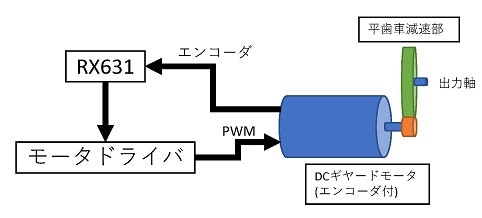
図1 DCモータシステム概要図

図2 DCモータシステム製作ハードウェア

表1 ハードウェア仕様

品目
エンコーダ付きギヤードDCモータ	1524 G0722(Aliexpressより購入)
定格電圧[V]	12
エンコーダパルス数[pulse/回転]	512
ギヤード部減速比	19:1
モータドライバ	DRV8832(秋月モジュール)
制御用マイコン	RX631(R5F5631FDDFP)
平歯車減速部の減速比	50:12

マイコンでモータの回転数を計測する

位相係数モードについて

　本実験で用いたRenesas製マイコンRX631シリーズには，位相係数モードと呼ばれる信号処理用のモードが存在する．そのため，エンコーダから出力されるA,B相信号を適切に入力することで，回転方向に応じてアップカウント及びダウンカウントを行う．ユーザ側は，任意周期でカウント値を参照することで，エンコーダ角度(つまり，モータ角度)を計測できる．また，角度情報を微分することによって，角速度を算出することが可能である．

角度・角速度計測について

　通常のエンコーダはA,B相から構成され，エンコーダによっては，原点用のZ相が存在する．今回は，A,Bの2相から構成されるエンコーダを使用した．A,B相は位相が$\pi/2$ずれた波形であり，
その位相差から回転方向を判定できる．また，角度・角速度の計測には主として2通りの方法があげられる．

1. 単位時間当たりのパルス数を計測する．角度はパルス数の積算値を用い，角速度は角度から数値計算で微分値を求める．
2. 任意のパルスから次のパルスまでの時間を計測する．角度は時間の計測ごとにエンコーダのパルス辺りの単位角度だけ積算することで求める．角速度は，
   計測した時間を利用して求める．エンコーダの分解能が低く，計測対象に対して，重視されるのが角速度である場合に適する．ただし，静止状態の場合の計測には実装上の工夫が必要となる．

　今回は1つ目の方式を用いた．RX631マイコンの位相係数モードでは，A,B相を適切な端子に接続することで，正転時にはパルスごとにカウントアップを，逆転時にはパルスごとに
カウントダウンを行う．そのため，計測周期ごとにカウントレジスタの値を読み取ることで，計測周期ごとのパルス数の積算値(=角度)を計測できる．
　ただし，カウンタは16bit(=65535)であるため，回転時にはオーバーフローやアンダーフローを生じる．そのため，初期位置からの絶対角度を必要とする場合には，オーバーフロー，アンダーフローを検知した場合には，その回数を記録し，適切なオフセットを施す必要がある．

例)エンコーダパルス数512pulse/rのエンコーダの場合．
オーバーフロー回数を$N_{of}$，アンダーフロー回数を$N_{uf}$とする．カウンタ値=$N_{cnt}$の時の絶対角度$\theta_{abs}$は次式により求められる．

\theta_{abs}[rad]=\frac{(N_{of}-N_{uf}) \times 65535 + N_{cnt}}{512} \times 2\pi

通常は，モータ出力軸(=エンコーダ測定対象の軸)から，減速されたものが出力軸となり，計測対象は出力軸であるため，式(1)の値が減速比で除されたものが出力軸角度となる．

制御理論

PID制御について

　代表的な制御方式としてPID制御がよく用いられる．PID制御は，指令値と出力の偏差に対して，偏差に対する比例(P)値，積分(I)値，微分(D)値の合計値を出力するものである．
　非常に多くの参考書・参考サイトが存在するため，詳細は割愛するが，一般的には各パラメタ($K_p,K_I,K_D$)を試行錯誤的に調整することで，制御を実現する．

状態フィードバック制御

　PID制御に対して現代制御で最も基本的なものが状態フィードバックである．これはPID制御とは異なり，出力値を含めた対象システムの状態量$x$をフィードバックする．
この時のフィードバックの係数を求める方法の一つとしてLQRと呼ばれる方法が存在する．またそれを拡張したものとしてLQIと呼ばれるようなものも存在する．これらについては，
理論的な説明が非常に煩雑である．そのため，参考文献を末尾に紹介するにとどめる．今回は実際にLQI制御を用いているが，パラメタに関してはMATLABを使用することで
容易に求めることが可能である．理論自体は非常に興味深いものであるため，これまでPID制御のみを用いてきた方々には是非とも参考文献を参照していただきたい．

DCモータシステムの微分方程式

図3 DCモータシステムモデル

DCモータシステムモデルは図3のように設定した．
よって，電気回路に関する微分方程式は次である．

u=R_a i+L_a \frac{di}{dt}+V_{be}

また，逆起電力定数$k_v$について次式が成立する．

V_{be}=k_v \frac{d\theta_M}{dt}

モータの発生トルクを$T_M$とすると，トルク定数$k_t$について次式が成立する．

T_M=k_t i

DCモータのインダクタンス成分は非常に小さいので，$L_a\approx0$とすると式(2)，(3)，(4)から次式を得る．

u=R_a \frac{T_M}{k_t} +k_v \frac{d\theta_M}{dt}

一方で，出力軸に生じるトルクを$T$とすると，出力軸の回転運動方程式は，次のとおりである．

T=J\frac{d^2 \theta}{dt^2} + f\frac{d\theta}{dt}

ここで，減速比が$n:1$であることからモータと出力軸間には次式の関係が成立する．ただし，減速機の効率が1とした．

\begin{align}
\theta &=\frac{1}{n}\theta_M \\
T &=nT_M
\end{align}

よって，式(5)に式(6)，(7)，(8)を代入することにより次のように変形される．

\begin{align}
u &=\frac{R_a}{nk_t}T+nk_v\frac{d \theta}{dt}\nonumber \\
 &=\frac{JR_a}{nk_t}\frac{d^2 \theta}{dt^2} + \frac{fR_a}{nk_t}\frac{d\theta}{dt}+nk_v\frac{d \theta}{dt}\nonumber \\
 &=\frac{JR_a}{nk_t}\frac{d^2 \theta}{dt^2}+\frac{n^2k_t k_v + R_a f}{n k_t}\frac{d\theta}{dt}
\end{align}

以上から，DCモータシステムの電圧$u$と出力軸角度$\theta$の関係式を導くことができた．

DCモータシステムの電圧/角度伝達関数

本節では，電圧/角度伝達関数を求める．但し，$\alpha,\beta$を次式のように定める．

\alpha=\frac{JR_a}{nk_t},\beta=\frac{n^2k_t k_v + R_a f}{n k_t}

その上で，式(9)を初期値0としてラプラス変換すると，

U(s)=s\alpha \Theta(s) + s^2\beta \Theta(s) \nonumber \\
\therefore \frac{\Theta(s)}{U(s)}=\frac{1}{\beta} \times \frac{1}{s^2 + \frac{\alpha}{\beta} s} %\dotが使えないようだから，\timesで代用

となる．

DCモータシステムの状態空間モデル

DCモータシステムのモデルからその状態空間モデルを導出する．式(9)を$\frac{d^2 \theta}{dt^2}$について整理すると，

\frac{d^2 \theta}{dt^2}=-\frac{n^2 k_t k_v + R_a f}{R_a J}\frac{d \theta}{dt} + \frac{n k_a}{R_a J}u

となる．ここで状態量$x(t)$，出力$y(t)$を

x(t)=\left( \begin{array}{c}
\theta \\
\frac{d \theta}{dt} \\
\end{array} \right),
y(t)=\left( \begin{array}{c}
\theta \\
\frac{d \theta}{dt} \\
\end{array} \right)

と設定する．すると，状態方程式は，

\begin{align}
\frac{dx}{dt} &=A_{dc}x+B_{dc}u\\
y &=C_{dc}x
\end{align}

ただし，

\begin{align}
A_{dc} &=\left( \begin{array}{cc}
0 & 1\\
0 & -\frac{n^2 k_t k_v + R_a f}{R_a J}
\end{array} \right),
B_{dc}=\left( \begin{array}{c}
0 \\
\frac{n k_a}{R_a J}
\end{array} \right)  \\
C_{dc} &=\left( \begin{array}{cc}
1 & 0\\
0 & 1
\end{array} \right) 
\end{align}

と表現される．以上から，DCモータシステムの状態空間モデルが導かれた．

システム同定について

システム同定とは

　対象システムを表現するモデルを構築することをモデリングと呼ぶ．多数のモデリング手法が存在し，そのため，どのようなモデリング手法により，どのようなモデルを構築するかは非常に重要である．その中でも，数式モデルと呼ばれるような，システムを各種数式で表現したモデルがある．
　今回はシミュレーションや制御器設計を行うことが目的であるため，対象とするDCモータシステムの数式モデルを求める必要がある．数式モデルには主に次の3種類のモデルに大別される．

1. ホワイトボックスモデル
   ホワイトボックスモデルは，モデリング対象の構造が完全に既知な状態にあるモデルある．一般的には対象のふるまいが，運動方程式や，回路方程式等で全て表現することができるような場合に用いられる．
2. ブラックボックスモデル
   ブラックボックスモデルは，モデリング対象の構造が一切不明な状態にあるモデルである．そのため，通常はその入出力のみを扱うこととなり，そのモデル表現は必ずしも，実システムと一致する必要はない．
3. グレーボックスモデル
   グレーボックスモデルは、ホワイトボックスモデルとブラックボックスモデルの中間に位置するモデルである．対象の一部の物理情報のみが既知の場合に利用される場合がある．

　対象システムが小さい場合には，ホワイトボックスモデルとして扱うことができることも多い．しかし，多くの実システムでは数式では表現できない要因が存在することが多い．そのため，対象システムをブラックボックスモデルとみなし，その入出力からモデルを推定する．このような入出力からモデルを作成することをシステム同定と呼ぶ．

システム同定の手順

　本書ではDCモータシステムを制御対象とした．そのため，同定対象は線形時不変である．また，内部に閉ループを持たない．以上の条件で今回用いる同定方法について記す．但し，システム同定には非常に多くの方法が存在し，適切な手法を選択することは難しい．一般的なシステム同定の手順を次に示す．

1. 同定実験の設計
   同定入力やサンプリング周期の選定を行う．この時，必要であればプレ同定を行い，対象モデルについての概観を得る．
2. 同定実験
   対象システムの入出力データの収集を行う．
3. 測定データの前処理
   測定データには，ドリフトやバイアス，ノイズ等の同定結果に悪影響を与える要素が存在する場合がある．そのため，それらを適切に処理する．
4. 構造同定
   どのようなモデル構造とするかを検討する．但し，本書では，伝達関数と状態空間モデルで対象をモデリングすることとした．そのため，この項目については実際の実験では省略する．
5. システム同定法
   前項で決定したモデルに対して，各種の同定法を用いることでそのパラメタを推測する．
6. モデル妥当性の評価
   得られたモデルが妥当なモデルであるかを評価する．

以上の手順を通して，対象システムのモデルを得る．

同定入力の選定について

　システム同定を行う上で，対象システムに入力する同定入力は、優れた同定結果を得るために非常に重要な要素である．同定入力について簡単に解説する．
　同定入力には，振幅特性と周波数特性が重要である．

1. 同定入力の振幅特性について
   同定入力の振幅を選定するには多くの要素が存在する．その中でも特に代表的なものとして次の3つがあげられる。
   • 飽和
     理想的なシステムのアクチュエータには，無限の出力が許容される．しかし実際のシステムでは，アクチュエータは一定の入力以上の大きさでは出力値が一定になる．このような出力の飽和であったり， 可動域から生じる角殿飽和等、実システムには非常に多くの飽和要素が存在し，それによりシステムが非線形となる．そこで，システム同定ではこのような飽和領域に入らないように，振幅を選択する必要がある．
   • 不感帯
     対象とするシステムによっては，入力が小さい場合にはシステムが理想的動作しない場合がある．例として，DCモータの場合には，入力電圧が小さい場合には回転軸の静止摩擦力により回転しない場合がある．このような，非線形性も存在する．そのため，振幅をある程度大きくする必要がある．
   • 出力信号の対雑音性能(SN比)
     実際のシステムでは，出力信号の計測には雑音が混入する．入力振幅が小さい場合には，相対的に出力信号の計測結果に対する雑音の影響が大きくなり，出力信号のSN比が悪化する．そのため，入力信号は可能な限り大きい方が望ましい． 以上のような要素を考慮しながら，適切な振幅を選択する必要がある．
2. 同定入力の周波数特性について 同定のためには，対象システムの全モードを励起する必要がある．そのため，同定入力が多数の周波数成分を含んでいる必要がある． 理想的な白色雑音は全ての周波数成分を含むことから，同定入力に適切な信号である． しかし，理想的な白色雑音は物理的に困難である．そのため，ある規則に基づき疑似不規則信号を生成することで代用する．その中でも，同定入力によく使用される信号系列としてM系列信号があげられる．本書でもこのM系列信号を同定入力として用いる．

M系列信号

1. M系列の生成方法 周期$N=2^n-1$のM系列は，式(15)によって生成される．

x_k=a_1 x_{k-1}\oplus a_2 x_{k-2} \oplus \cdots \oplus a_n x_{k-n}

ここで$\oplus$は排他的論理和EXORを表す．また，初期値には$\forall x = 0$でなければよい．
これはn段のシフトレジスタを用いて構成されるが，このとき、最終段は常にフィードバックされる必要があるので$a_n=1$となる．

2. M系列の性質
システム同定用の不規則信号は通常+1と-1であらわされるので，式(\ref{15)により生成される系列のうち0を-1としたうえで，時間$T$ごとにホールドした時間関数を用いればよい．ここで，実際に生成したM系列信号について，自己相関関数とパワースペクトルを求めたものを図4として示す．
　図4から明らかなようにラグが1のとき以外には自己相関は小さい．またパワースペクトルが全域にわたって平坦な周波数特性を有していることが確認できる．このような特性を持つため，M系列信号は同定入力とすることに適している．

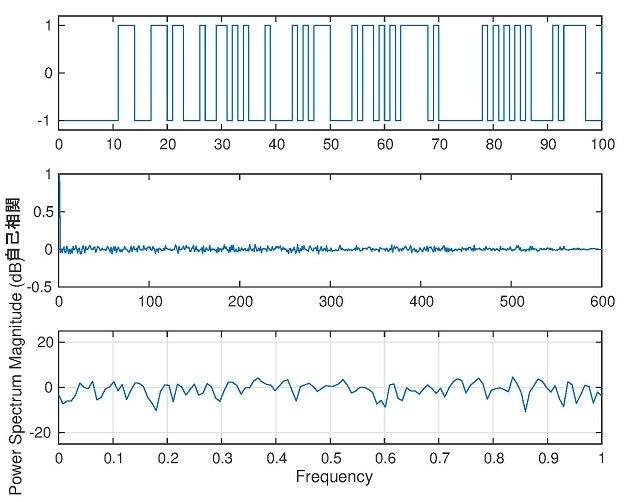
図4 M系列を利用した2値信号の自己相関とパワースペクトル

3. シフトレジスタ数nの選択について
同定入力としてM系列信号を利用する場合に，シフトレジスタ数nを選択する必要がある．但し，nをいたずらに大きくしても，必ずしも同定精度が向上するわけではないことに注意すべきである．M系列信号は信号の1周期全体でもって疑似白色信号となるためである．つまり，同定実験に要する時間($T_{exp}$とおく)は，M系列信号の１周期の長さ以上でなければならない．よって，最低でも式(16)を満たす必要がある．

(2^n-1)T_M \leq T_{exp}

但し，$T$は制御入力の単位ホールド時間(つまり，M系列信号のサンプリング時間)である．
一般には$T_{exp}$をM系列の１～2周期の時間とすることが多い．
次に，M系列信号と立ち上がり時間との関係を考える．M系列信号の1周期中に+1がn回続くのは1回だけであるため，この状態が最大持続時間となる．対象システムの正確な同定のためには，この最大持続時間が立ち上がり時間($t_R$)よりも長い必要がある．よって，次式(17)を満たす必要がある．

nT> t_R

よって，式(17)から、最大連続パルス数$n$は次式(18)を満たす．

n>\frac{t_R}{T}

しかし，実際に式(17)を満たす$n$を求めるとサンプリング周期$T$が短い場合に非常に大きなnが選択されてしまうことがある．
そこで，実際のサンプリング時間の整数倍の時間をM系列のサンプリング時間とすることによってnを小さくする手法が用いられる．つまり，

T_M=pT

とする．これを式(17)に代入することで，

n>\frac{t_R}{pT}

と変形される．よって，pを調整することで，nの値を増減することが可能となる．ただし，pを増加させることは，M系列信号の周波数帯域を減少させることとなってしまうため，一般には$p \leq 4$程度が用いられる．

同定実験のサンプリング周波数

システム同定における経験的なサンプリング周期の選定法として
次のような方法が経験則的に用いられている．

1. 同定対象のバンド幅の10倍程度のサンプリング周波数を用いる．
2. 同定対象のステップ応答における立ち上がり時間の間に5~{}8サンプル点が入るくらいのサンプル周期を利用する．
3. 同定対象のステップ応答が定常値の$95\%$に達する時間を$T_{95}$として，次式(21)を満たすサンプリング時間$T$を用いる．

\frac{1}{15}T_{95} \leq T \leq \frac{1}{4}T_{95}

一方で，事前に対象システムの特性が分からない場合には可能な限り高速にサンプリングを行う．そうすることによってデータ処理時にダウンサンプリングで対応できるためである．

ドリフト/バイアスとは

実験で計測したデータには，システム同定のために適切ではない要素(ノイズ等)が含まれている．ドリフトとバイアスは，データに対する一次近似式で表わされる．

y=ax+b

ここで$a$が0でなければドリフトが存在し，また，$b$が0でなければバイアスが存在する．同定のためにはデータからこれらの要素を除去する必要があるようだ．

DCモータの伝達関数のシステム同定

プレ同定

今回はDCモータシステムの同定のために，M系列信号を用いることとする。そのため，同定用の入力信号の各種パラメタを適切に設定する必要がある。
そこで，対象のステップ応答を取得することにより，同定用の入力信号を選定する。
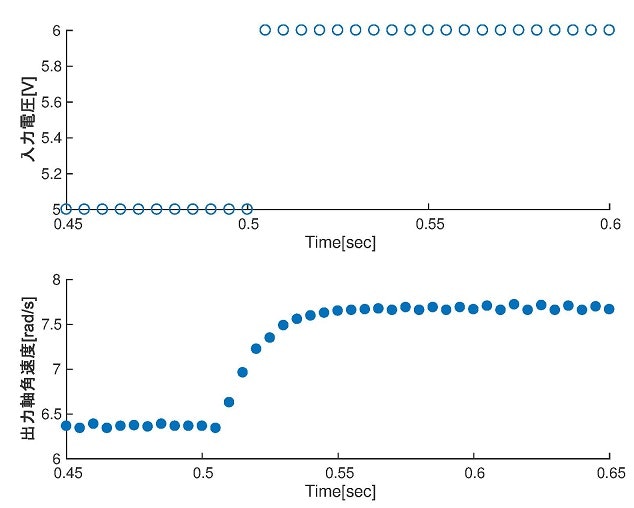
DCモータは一般に静止状態では軸の静止摩擦力が作用し，適切なステップ応答を得られないと考えられる．そのため，回転中に入力電圧を変化させることで，ステップ応答を計測した．具体的な実験条件は表2のように設定した．
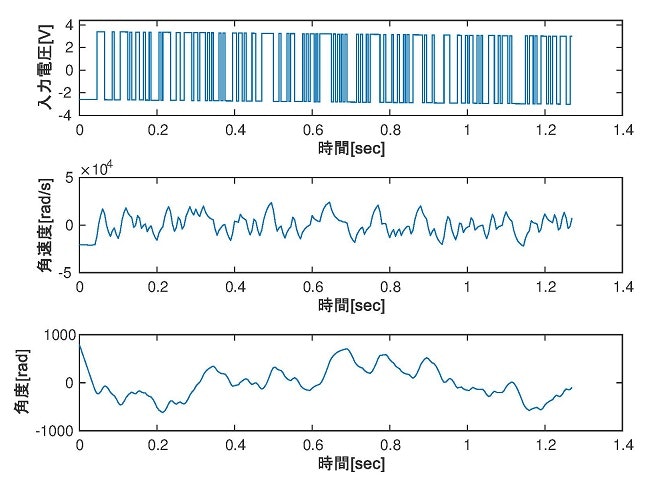
実験結果を図5に示す。図5から、その立ち上がり時間$T_R = 0.045sec$である。この時，立ち上がり時間の間にサンプリング点が10点存在する．
今回の実験では，事前に設定したサンプリング時間が条件を満たす．よって，今後は同様のサンプリング時間$T_s=0.005$を用いる．但し，うまく同定ができない場合にはサンプリング時間を再度考慮する必要がある．

表2 プレ同定用のステップ応答の実験条件

1	2
回転方向	正転
初期電圧[V]	5
最終値電圧[V]	6
サンプリング時間[sec]	0.05

図5 プレ同定用の角速度ステップ応答

同定入力信号の検討

　プレ同定の結果として，1V振幅時の立ち上がり時間が$T_R=0.045sec$であることが分かった．同定実験では入力信号の振幅を6[V]に設定した．そのため，立ち上がり最低値から最大値までの立ち上がり時間は，$T_R'=0.27sec$と予想される．よって，式(18)を満たす最小の整数nは，$n=6$である．同定実験をM系列の1周期分の時間を行う場合に要する時間は次のように計算された．

\begin{align}
M系列周期サンプリング点数N &=2^6-1  \nonumber \\
 &=64
\end{align}

\begin{align}
M系列1周期の時間[sec] &=64\times T_s \nonumber \\
 &=0.32
\end{align}

よって，2周期の実験に要する時間は6.4secである．そのため，$n=6$に設定した．
　以上から，同定入力信号として設定したM系列信号の仕様を表3とした．DCモータは電圧0付近では軸の摩擦等の影響が大きくなる可能性があったため，一定方向回転時の応答を計測し，そのオフセットを除くこととして同定を行った．

表3 同定実験用M系列信号の仕様

1	2
シフトレジスタ数n	6
M系列信号周波数[Hz]	200
振幅[V]	3
オフセット電圧[V]	6
データサンプリング時間[sec]	0.005
1周期の時間[sec]	0.32

同定実験の実施

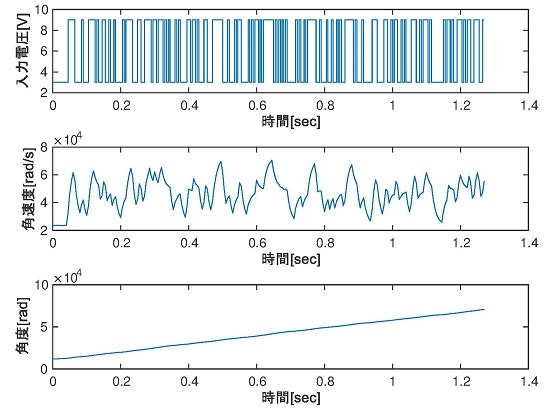
　前節から，同定のためのM系列信号の仕様を決定することができた。また、同定作業がうまくいかない場合には、再度、入力信号について検討することが非常に重要である．表3の同定入力を用いた同定実験の結果を図6として示す．ここでモータ角度が明らかにドリフトしているのは，入力電圧にオフセットを生じさせた状態(一方向に回転し続けている状態)で実験を行ったためである．また，この時に，M系列信号生成のために利用したMATLAB用Mコードは次のものである．

%同定入力の生成
Amplitude=[3,9];%[信号の最小値,最大値]
band = [6,1];%[シフトレジスタ数n,M系列のクロック周波数]
u=idinput(256,'prbs',band,Amplitude); %(データ数，以下略)
t=0:0.005:(length(u)-1)*0.005;
stairs(t,u);axis([t(1) t(end) 0 10]);

図6 同定実験の入出力測定値

MATLABによる伝達関数の同定

　図6の結果から，DCモータシステム電圧-角度伝達関数を同定した．適宜、使用したMATLAB用のMスクリプトについても掲載する．

1. 実験データの切り出し
   今回の実験では，計測データに問題が見られなかったため，データの切り出しを行わずに同定を進める．同定対象や実験構成によっては，初期の立ち上がりの部分を削除する必要がある場合もある．

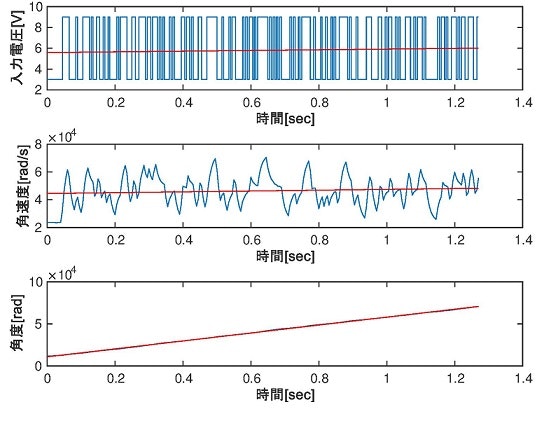
2. ドリフト/バイアスの有無の判定
   
   ドリフトとバイアスについて検証するために測定データに対して１次近似式を求め，それを図示した．図7から,実験データにはドリフトとバイアスの両方が存在することが判明した．

   %データの読み込み
   %読み込み元データ　時間，入力電圧，角速度(エンコーダ生値=減速以前)，角度(エンコーダ生値=減速以前)
   %先頭にラベル名が存在する
   [numeric , txt] = xlsread('id_data_ts5ms.xls'); 
   t = numeric(:,1);
   U1 = numeric(:,2);
   Y1_vel = numeric(:,3)./(19 * (50/12));  %係数はエンコーダ値を出力軸の角度，角速度に変換するためのものである．
   Y1_ang = numeric(:,4)./(19 * (50/12));
   
   % データの評価
   % ドリフト（低周波外乱）の有無，バイアス（直流成分）について考察
   PU1 = polyfit(t,U1,1);  %1次近似式の係数
   VU1 = polyval(PU1,t);  %1次近似式の値
   PY1_vel = polyfit(t,Y1_vel,1);
   VY1_vel = polyval(PY1_vel,t); 
   PY1_ang = polyfit(t,Y1_ang,1);
   VY1_ang = polyval(PY1_ang,t); 
   
   % 実験データのグラフ化(ドリフトとバイアスを赤線で表示
   figure();
   subplot(3,1,1);
   stairs(t,U1);ylabel(txt(1,2));xlabel(txt(1,1));
   hold on;plot(t,VU1,'r');hold off;
   ylim([(min(U1)-1),(max(U1)+1)]);
   subplot(3,1,2);
   plot(t,Y1_vel);ylabel(txt(1,3));xlabel(txt(1,1));
   hold on;plot(t,VY1_vel,'r');hold off;
   subplot(3,1,3);
   plot(t,Y1_ang);ylabel(txt(1,4));xlabel(txt(1,1));
   hold on;plot(t,VY1_ang,'r');hold off;
   

   
   図7 測定データとそれに対する一次近似

3. 実験データからドリフト/バイアスの除去
   
   実験データからドリフトとバイアスを除去した結果を示す．

   %平均値除去(バイアス除去)
   U2=detrend(U1,'constant');
   Y2_vel=detrend(Y1_vel,'constant');
   Y2_ang=detrend(Y1_ang,'constant');
   %トレンド除去
   U3 = detrend(U2);
   Y3_vel = detrend(Y2_vel);
   Y3_ang = detrend(Y2_ang);
   
   % 結果を表示
   figure()
   subplot(3,1,1);
   stairs(t,U3);ylabel(txt(1,2));xlabel(txt(1,1));
   ylim([(min(U3)-1),(max(U3)+1)]);
   subplot(3,1,2);
   plot(t,Y3_vel);ylabel(txt(1,3));xlabel(txt(1,1));
   subplot(3,1,3);
   plot(t,Y3_ang);ylabel(txt(1,4));xlabel(txt(1,1));
   

   
   図8 ドリフト/バイアスを除去した同定実験データ

4. 同定用データセットと検証用データセットへの実験データの分割
   
   　実際に同定実験を行ったデータセットを分割することで，同定作業に用いるデータと同定結果に対する検証を行うためのデータに分割する．

   % 検証用にデータ分割
   % 誤差を防ぐために，t2のデータ-0.8の絶対値がespより小さいデータの番号とする 
   No2 = find(abs(t - 0.8) <=eps );
   % 前半データ
   U4_pre = U3(1:No2);
   Y4_vel_pre = Y3_vel(1:No2);
   Y4_ang_pre = Y3_ang(1:No2);
   % 後半データ
   U4_post = U3(No2:end);
   Y4_vel_post = Y3_vel(No2:end);
   Y4_ang_post = Y3_ang(No2:end);
   

5. 伝達関数の同定
   
   　本実験ではMATLABのpem関数を用いることで予測誤差法(PEM)によって同定を行った．予測誤差法は予測誤差から構成される評価関数を最小化するような手法の総称である．電圧-角度伝達関数の同定結果は式(25)となった．同定結果に対して検証用データセットを用いた検証結果を図に示した．

   %iddatオブジェクトの定義
   Ts = 0.005; %同定データサンプル時間[s]
   %同定用データセット
   iddataset_ang = iddata(Y4_ang_pre,U4_pre,Ts);
   %検証用データセット
   iddataval_ang = iddata(Y4_ang_post,U4_post,Ts);
   
   %予測誤差法(PEM)によるモデル同定
   %伝達関数の同定(角度)
   m1 = pem(iddataset_ang);    %状態空間モデル(離散系)
   m2 = tf(m1);    %伝達関数モデル(離散系)
   m3 = d2c(m2)    %伝達関数モデル（離散系から連続系に変換）
   
   %同定結果の検証
   figure();
   compare(iddataval_ang,m1);
   

G(s)=\frac{0.1542 s^2 + 115.5 s - 1819}{s^3 + 112.8 s^2 + 385.6s + 35580}

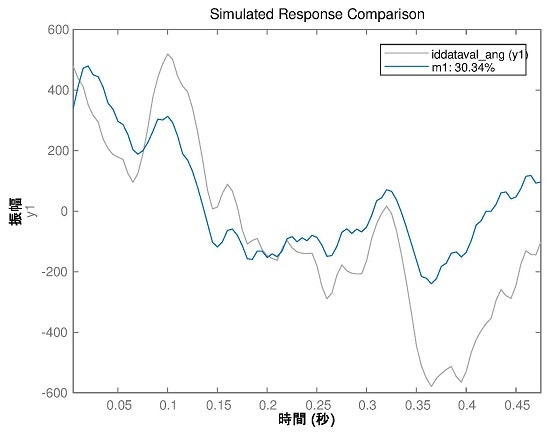
図9 電圧-角度伝達関数の検証結果

6. 状態空間モデルへの同定

状態空間モデルに対して同定を行った．この時，DCモータシステムモデルの状態方程式の構造は既知である．そのなかで，不明なパラメタをNaNとして表現したものが次式である．

\begin{align}
\frac{dx}{dt} &=Ax+Bu\\
y &=Cx+Du
\end{align}

ただし，

x=\left( \begin{array}{c}
\theta \\
\frac{d \theta}{dt}
\end{array} \right),
y=\left( \begin{array}{c}
\theta \\
\frac{d \theta}{dt}
\end{array} \right) \\
A=\left( \begin{array}{cc}
0 & 1\\
0 & NaN
\end{array} \right),
B=\left( \begin{array}{c}
0 \\
NaN
\end{array} \right) \\
C=\left( \begin{array}{cc}
1 & 0\\
0 & 1
\end{array} \right),
D=\left( \begin{array}{c}
0 \\
0
\end{array} \right) 

同定を行い求めた値は次のようになった．またこの時の検証結果を示す．

A=\left( \begin{array}{cc}
0 & 1\\
0 & -117.1
\end{array} \right),
B=\left( \begin{array}{c}
0 \\
99.16
\end{array} \right) 

```
% 状態空間モデルの同定
u = U4_pre;
y = [Y4_ang_pre Y4_vel_pre];
z = iddata(y,u,0.005);
u_post = U4_post;
y_post = [Y4_ang_post Y4_vel_post];
z_post = iddata(y_post,u_post,0.005);

As = [0 1;0 NaN];
Bs = [0;NaN];
Cs = [1 0;0 1];
Ds = [0; 0];
Ks = [0 0;0 0];
X0s =[0 ;0];

A = [0 1; 0 -1];
B = [0 ; 0.28];
C = eye(2);
D = zeros(2,1);

ms = idss(A,B,C,D);

setstruc(ms , As , Bs , Cs, Ds, Ks, X0s);
set(ms,'Ts',0);

dcmodel = pem(z, ms ,'trace', 'on')
figure();
% compare(z,dcmodel);
compare(z_post,dcmodel);
```

![id_state_model.jpg](https://qiita-image-store.s3.amazonaws.com/0/203155/076d71e2-c550-ba99-5939-bbb3f6dfede9.jpeg)

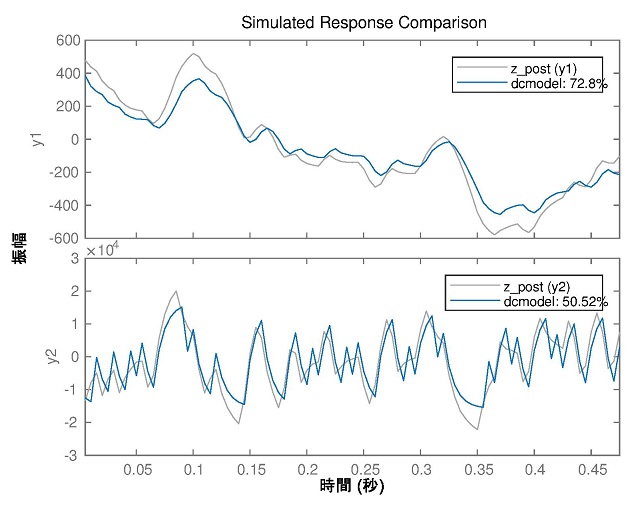
図10 状態空間モデルの検証結果

MATLAB/Simulinkによるシミュレーションの構築

MATLAB/Simulinkによるシミュレーション環境の構築

　MATLAB/Simulinkを用いたDCモータシステムのシミュレーション環境の構築を行った．シミュレーション条件を表4に示す．また，モデルの記述は同定モデルの検証結果から適合率の高かった状態空間モデルを採用した．構築したSimulinkモデルは図11に示す．
表4 Simulinkシミュレーション環境設定

1	2
MATLABバージョン	9.2(R2017a)
Simulinkバージョン	8.9(R2017a)
シミュレーション時間[sec]	10
ソルバータイプ	可変ステップ
ソルバー	自動
操作量	モータ端子関電圧[V]
制御量	出力軸角度[rad]

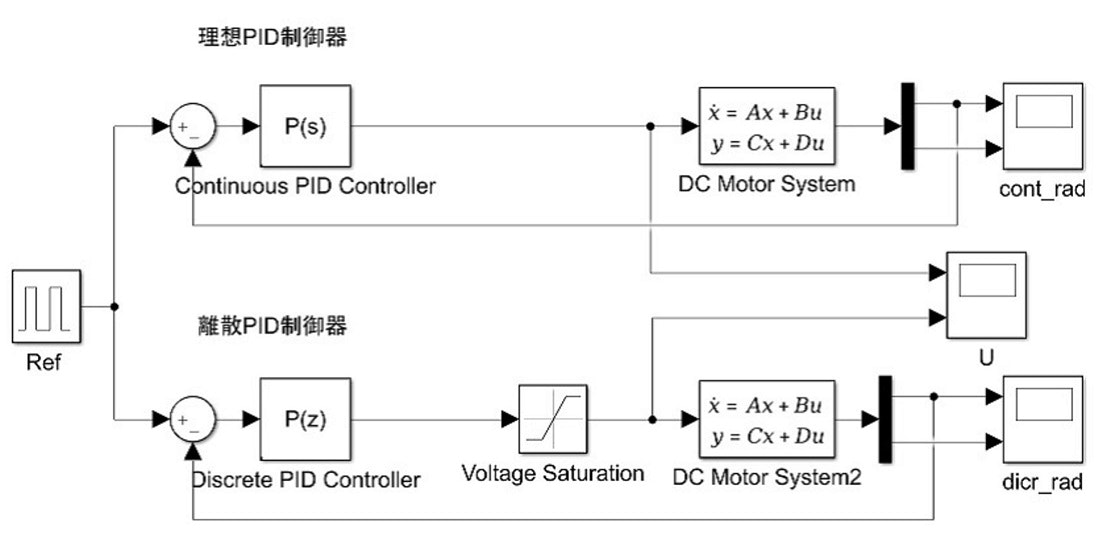
図11 状態空間モデルを用いたPID制御器用Simulinkモデル

同定結果を用いたPID制御パラメタの選択

　PIDパラメタの選択には非常に多くの方法が提案されている．代表的なものとしてはCHR法があげられる．しかし，本書の目的はシミュレーションと実機実験を関連付けることであり，パラメタ設定の詳細については，他の文献を参照していただきたい．ここでは，MATLAB/Simulinkの機能を用いて簡易的に調整を行う(PID制御ブロックをダブルクリック->調整．．．をクリック)．実際にパラメタの簡易調整を行った結果を図示した．またこの時の操作量についても図示した．また，比例係数$Kp=32.978$を，制御周期$T=0.01sec$とした．

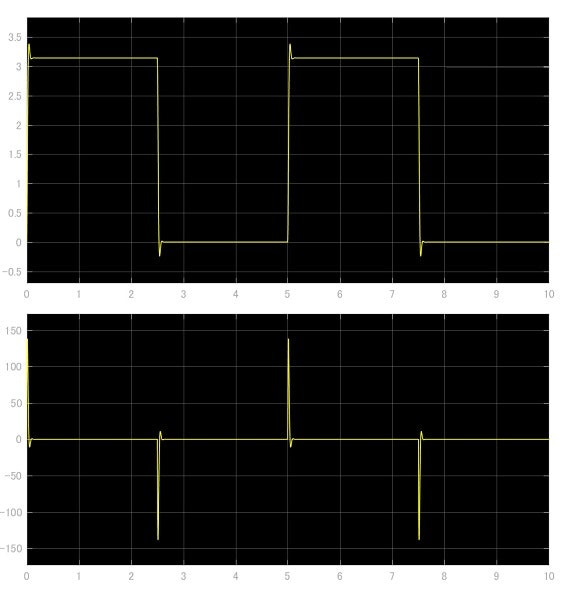
図12 理想的な連続系PID制御器を用いたP制御のシミュレーション結果

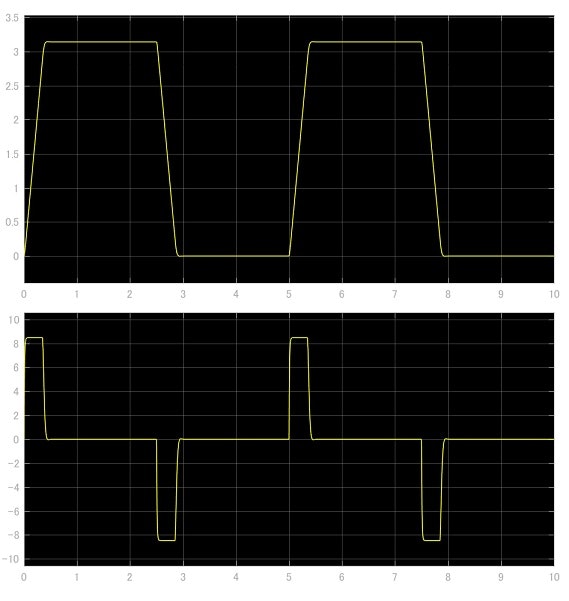
図13 操作量の飽和する離散系PID制御器を用いたP制御のシミュレーション結果

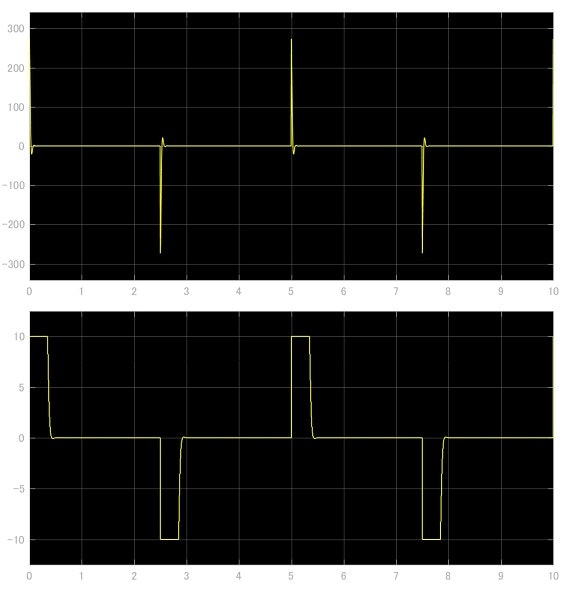
図14 連続・離散系PID制御器の操作量出力のシミュレーション結果

　図12，13から，理想的な制御器では非常に良い応答特性を示している．一方で，飽和制限のつく離散系制御器では立ち上がりが台形状となっている．しかし，図14から，理想的な制御器の出力はモータに対して300Vを超える電圧を印加しており，現実的ではない値になっている．

MATLAB/SimulinkによるSoftware In the Loop Simulation(SILS)

　実際に構築するための手順は次のとおりである．今回は参考としてC++で実装したPID制御器をSimulink内部で用いることで，その妥当性を検証することとした．なお，使用環境はMatlab2017 R2017aである．以前のバージョンの場合にはバグがありコンパイラのインストールがうまくいかないため本バージョンの使用を推奨する．

1. Matlabの上部アプリタブから，さらにアプリを取得を選択．左側の検索結果のタイプでフィルターのチェックボックスになにもチェックが入っていないことを確認してから，検索窓から，''mingw''を検索し，MATLAB Support for MinGW-w64 C/C++ Compiler　をインストールした．
2. コマンドラインから mex -setup　を入力した．MinGW以外のコンパイラがPCにインストールされていない場合には，次の工程へ進んだ．他のコンパイラがある場合には指示に従いMinGWをコンパイラとして設定した．
3. Simulink環境で，User-Defined Functionから，S-Function BuilderをSimulink空間に移した．
4. S-Function名を任意に設定した(sils_pidに設定)．
5. 初期化タブのサンプルモードを離散に，サンプル時間を設定(今回は0.01)した．
6. データプロパティタブで入力を設定した．今回は参照信号入力とと角度フィードバック入力を使うため，一つ追加し，入力をu0,u1とし，それぞれを参照信号，角度フィードバックとした．
7. データプロパティタブの出力で出力信号数等を設定できるが，今回は１つで良いためデフォルトのままとした．
8. 出力タブで出力部についてコーディングが行える．しかし，今回は後ほど自分でコーディングを行うため，デフォルトのままコメントアウト状態にする．
9. ビルド情報タブのTLCラッパーにチェックが入っていることを確認する．
10. ビルドボタンを押すと，sils_pid.c,sils_pid_wrapper.cが生成される．C++としてコーディングを行う場合には，これらの拡張子をcppに変更する．

11. sils_pid_wrapper.cpp(.c)を開き，sils_pid_Outputs_wrapper内部をコーディングすることでC(C++)での処理を実現する．ただし，このOutputsはS-Functionブロックの計算ステップごとに呼ばれる関数であるため，値を保持したい場合はstatic又は，グローバル変数を利用する必要がある．
    例として二つの入力の和を経過ステップ数nに応じて0.01n倍するコードを示す．

    void sils_pid_Outputs_wrapper(
                const real_T *u0,
                const real_T *u1,
                real_T *y0)
    {
        static float i=0;
        i+=0.01;
    
        *y0=(*u0+*u1)*i;
    }
    

12. コマンドラインで　mex sils_pid.cpp sils_pid_wrapper.cpp　と入力することで，S-Function用のmexがビルドされる．

13. Simulink環境で，User-Defined Functionから，S-FunctionをSimulink環境に移す．また，S-Function Builder をコメントアウトする．

14. S-FunctionブロックからS-Function名とS-Functionモジュールを設定した(sils_pid)．

15. 構築したPID用SILSモデルを示す．
    
    
    
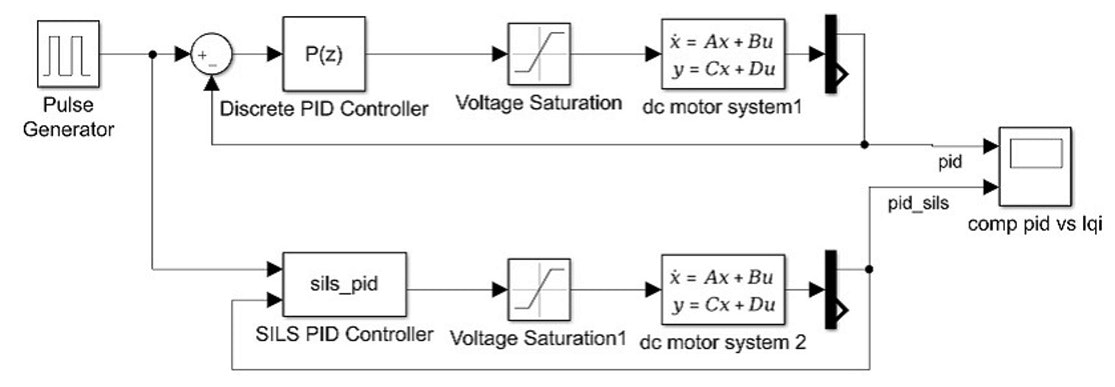
    図15 PID制御のSILSモデル
    
    　このとき，u0 参照信号，u1 角度フィードバック，y0 電圧出力としてコーディングを行った．実際にSILS環境下でP制御を行ったコードを以下に示す．
    PIDコントローラのテストとして次のようにwrapper.c(cpp)先頭で定義する．
    \#include "pid\_controller.h"

PidController pid_controller(
    50.536754973391, 0 , 0 ,0.01,0);

void sils_pid_Outputs_wrapper(
    const real_T *u0,
    const real_T *u1,
    real_T *y0)
{
    pid_controller.CalculateManipulatingVariable(*u1,*u0);
    float u_vol=(float)pid_controller.get_manipulating_variable_();
    *y0=u_vol;
}

　このときの出力結果を図16に示す．SimulinkのPIDブロックを用いたシミュレーション結果とS-Funcブロックを用いたC++コーディングによるシミュレーション結果は非常によく一致しており，コーディングしたコードは制御器として十分な性能を持っていると考えられる．SILSによって，実機以前にコードの検証が可能となり，バグの予防や異常動作による危険を避けることが可能となる．

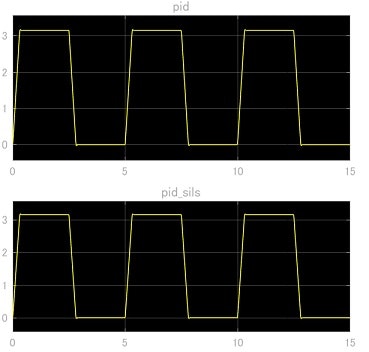
図16 PID制御のSILSのシミュレーション結果

DCモータの古典制御の実機実験

PID制御による角度制御実験

　本節では，シミュレーションにより求めたPID制御パラメタを用いて，実機による検証を行う．前章で求めたパラメタは比例項$Kp=32.978$ 制御周期$T=0.01sec$であった．この条件のもとで実際に実験を行った結果とシミュレーションの結果を図示する．なお，指令値は，0.2Hz，振幅$\pi[rad]$の矩形波を用いた．

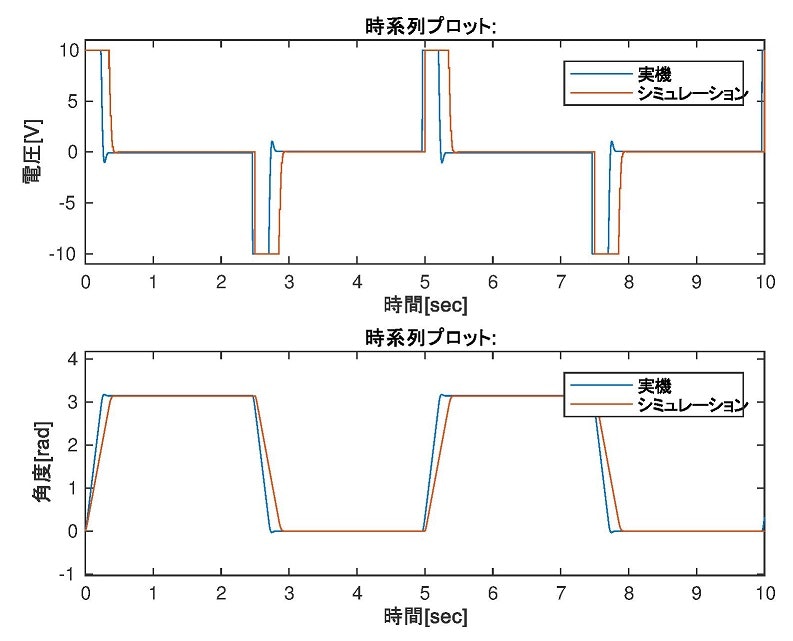
図17 P制御の実機実験結果とシミュレーション結果の比較

MATLAB/Simulinkによる現代制御シミュレーション

状態方程式を利用したDCモータシステムのシミュレーション環境の構築

　本章ではSimulinkを用いたDCモータシステムのシミュレーション環境の構築を行った．シミュレーション条件はPID制御のシミュレーション時と同様とした．また，モデルの記述はPID制御のシミュレーションと同じく，状態方程式表現を採用した．構築したSimulinkモデルは図18に示す．

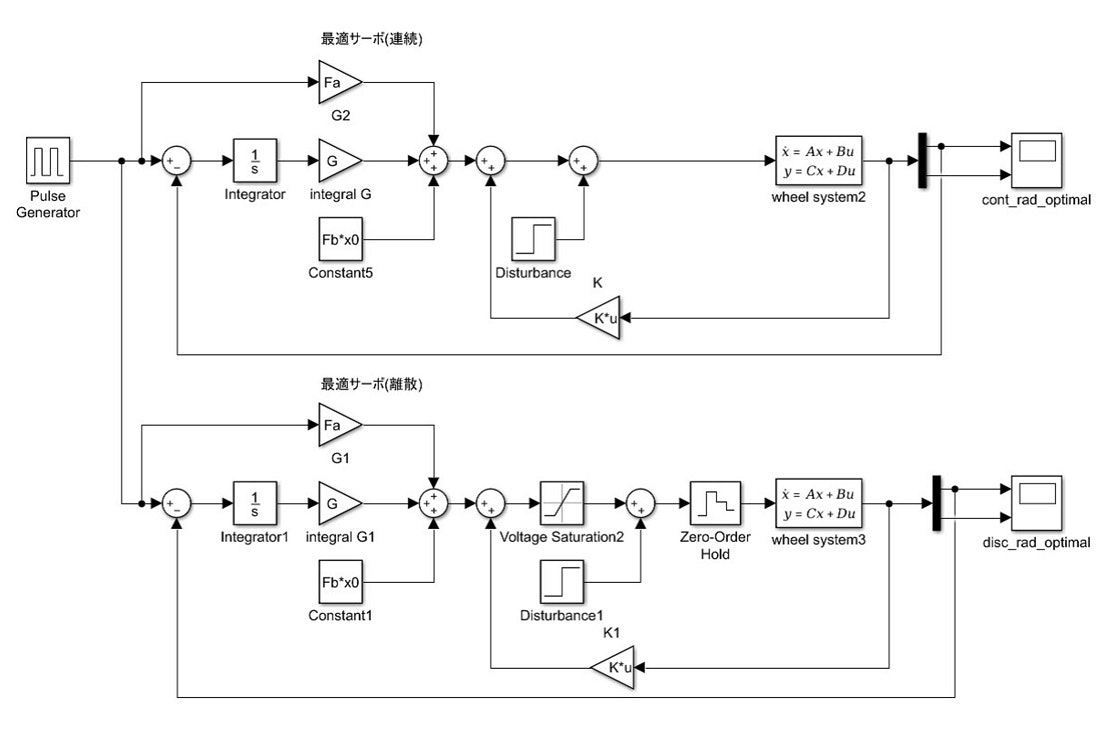
図18 状態空間モデルを用いたLQI制御器用Simulinkモデル
　LQI制御の場合にはPID制御の場合とは異なり，Simulink内部にLQI制御器ブロックが存在せず，離散時間での制御器を用いることができなかったため，ゼロ次ホールドを利用し，疑似的に信号を離散化した．
また，一定時間後にステップ上の外乱が加わるようにした．

LQIによるパラメタの算出

LQI制御では、そのパラメタである$Fa,Fb,K,G$は，評価関数に与えるQ,Rの値から計算される．通常このQ,Rを試行錯誤的に調整することが多い．今回は，Q,Rとして次の値を用いた．

Q=\left( \begin{array}{ccc}
1000 & 0 & 0\\
0 & 1000 & 0\\
0 & 0 & 100
\end{array} \right),
R=10

結果として求められた$Fa,Fb,K,G$は次式となった．

Fa=9.6220,Fb=\left( \begin{array}{cc}
0.7708 & 0.0061
\end{array} \right) \\
K=\left( \begin{array}{cc}
-10.3928 & -0.0856
\end{array} \right), G=3.1623

パラメタ算出のために用いたコードは次のとおりである．

%入力　u 端子関電圧[V]
%出力　y1 角度[rad], y2 角速度[rad/s]
A=[0 1;0 -117.1];
B=[0;99.16];
C=[1,0;0,1];
D=[0;0];

%最適サーボ
C_opt=[1,0];
Ae=[A zeros(2,1)
    -C_opt zeros(1,1)]
Be=[B
    0]

Q11=1000; Q22=100;
Qe=[C_opt'*Q11*C_opt zeros(2,1)
    zeros(1,2) Q22];
Re=10;

Pe=care(Ae,Be,Qe,Re);%リカッチ方程式の求解
P11=Pe(1:2,1:2);
P12=Pe(1:2,3);
P22=Pe(3,3);

K=-inv(Re)*B'*P11
G=-inv(Re)*B'*P12

M0=[A B
    C_opt 0]
Fa=[-K+2*G*inv(P22)*P12' 1]*inv(M0)*[zeros(2,1);1]
Fb=-2*G*inv(P22)*P12'

LQI制御による角度制御

　式(29)の時におけるLQI制御器の連続，離散系のシミュレーション結果を図19に示す．図19から、わずかに離散系の方が性能が悪いが，PID制御器の場合に比べれば，差異は小さいことが分かる．

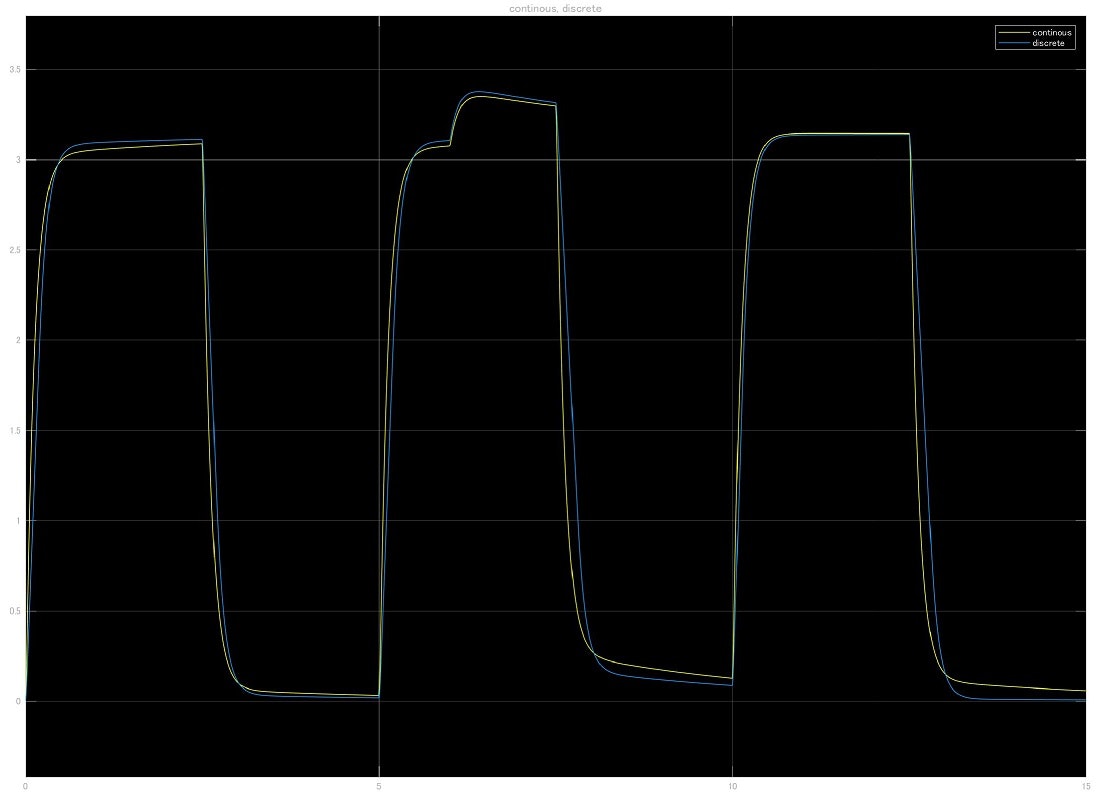
図19 LQI制御器のシミュレーション結果(連続，離散)

　次に，PID制御器とLQI制御器の結果を比較したものを図20に示す．このとき，6secでステップ上の外乱を印加した．図20から，PID制御器に比べてLQI制御器の方が優れたオーバーシュート特性を示していることが分かる．

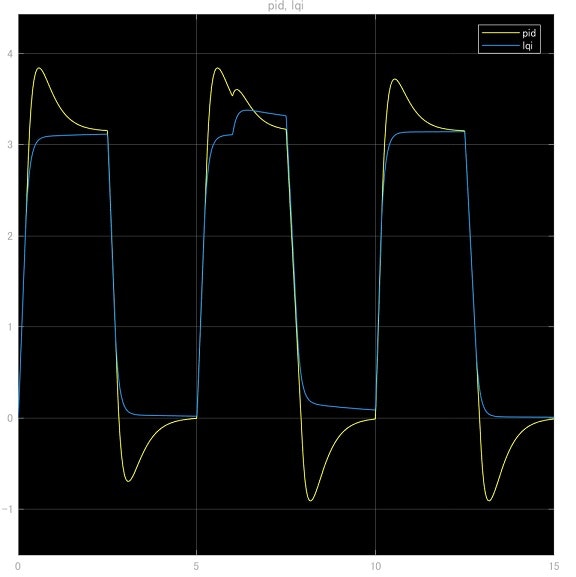
図20 PID制御器とLQI制御器の角度制御シミュレーション結果の比較

DCモータのLQI制御の実機実験

LQI制御による角度制御実験

　本節では，シミュレーションにより求めたLQI制御パラメタ式(29)を用いて，実機による検証を行った．実際に実験を行った結果とシミュレーションの結果を図示する．なお，指令値は，0.2Hz，振幅$\pi[rad]$の矩形波を用いた．図21から，シミュレーションに比べて実機の方が立ち上がり時間が短いことが分かる．一方で，波形の概径は一致していることも確認できた．

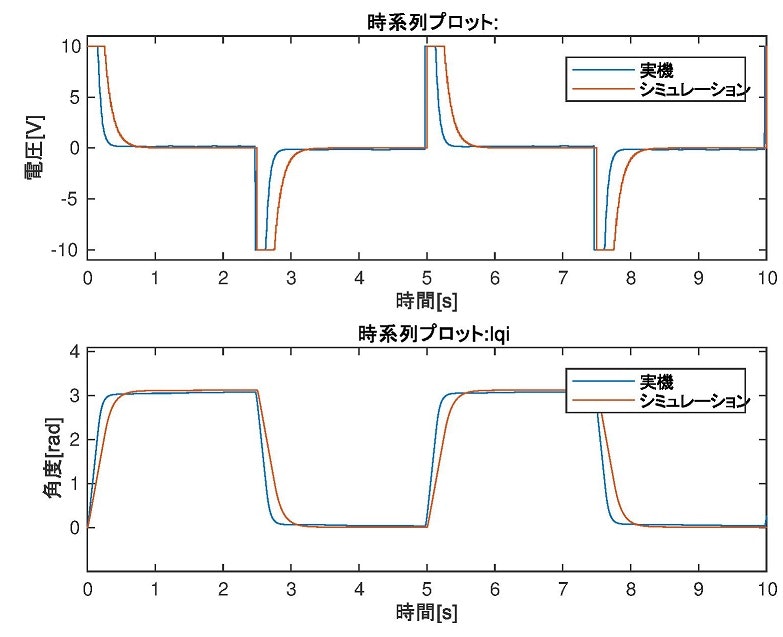
図21 LQI制御の実機実験結果とシミュレーション結果の比較

最後に

今回は制御工学の教科書にもっともよく出題されるDCモータを題材として，制御理論を実機に対して適用した．また，SILSによって実機検証以前に，制御に実際に用いるコードのテストができることを確認した．
全体を通して駆け足となってしまい，また，筆者の知識・実力不足から，不正確な記述となっている点も多々見受けられる．お気づきになられた方はコメント等宜しくお願いします．
机上の制御工学から実機における制御の世界へと沈んでいく一助と慣れればうれしい限りです．

参考文献

[1]MATLAB/Simulinkによるモデルベースデザイン入門・三田 宇洋
[2]MATLABによる制御のためのシステム同定・足立 修一
[3]MATLABによる制御のための上級システム同定・足立 修一
[4]MATLAB/Simulinkによる現代制御入門・川田昌克
[5]SimulinkとReal-Time Workshopを使ったMATLABによる組み込みプログラミング入門・大川　善邦

2017.09.26追加

制御した結果の動画を載せておりませんでしたので，upしました．
https://youtu.be/knRGY1BpRek