SVM(サポートベクトルマシーン)とは?
SVM (サポートベクトルマシーン)は教師あり機械学習の回帰と分類両方に使える学習法です。
例えば、下の図のようにX1とX2の2次元の特徴量でサンプルを分類する時、緑と黄色の線のような境界線を引くことができます。
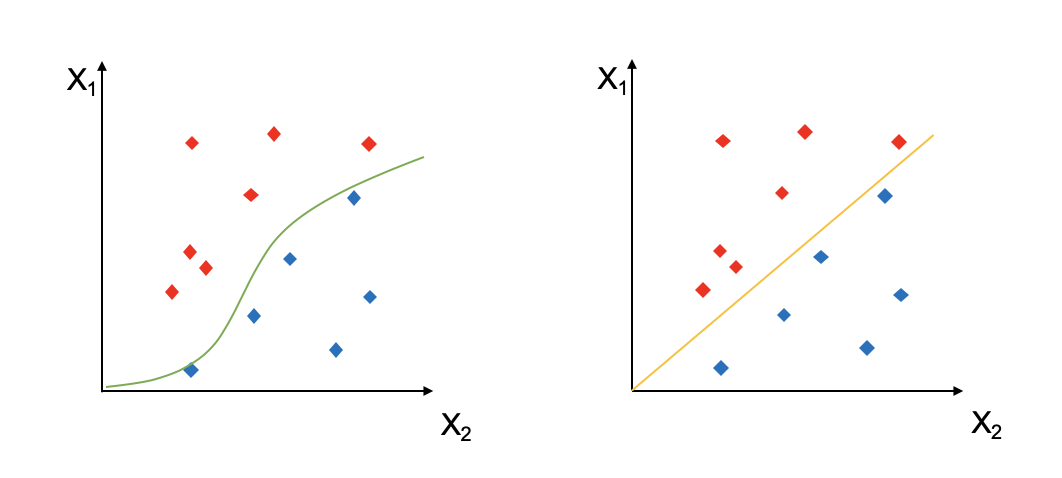
上の例では、2次元上でデータを分類するSVMでした。
では、これを3次元上で分類してみます。すると、下の図のように、データが平面で分類されました。入力データは変わらず2次元ですが、境界の関数は3次元になることが分かります。

このようにSVMでは、入力されたN次元の特徴量をもつデータをM次元の特徴量空間に拡張して分類を行うことができます。この境界となる線や面のことを **超平面(Hypter Plane)**と呼びます。
マージン最大化
超平面を決める上でマージン最大化と呼ばれる手法が使われます。
下の図をご覧ください。まず、超平面を決める上で、全てのデータポイントではなく、サポートベクトルと呼ばれるいう境界の近くにあるデータポイントだけを使用します。各クラスに所属するサポートベクトルからの距離をマージンと呼びます。マージン最大化ではこの赤クラスと青クラスからのマージンが最大になるような境界面を設定します。
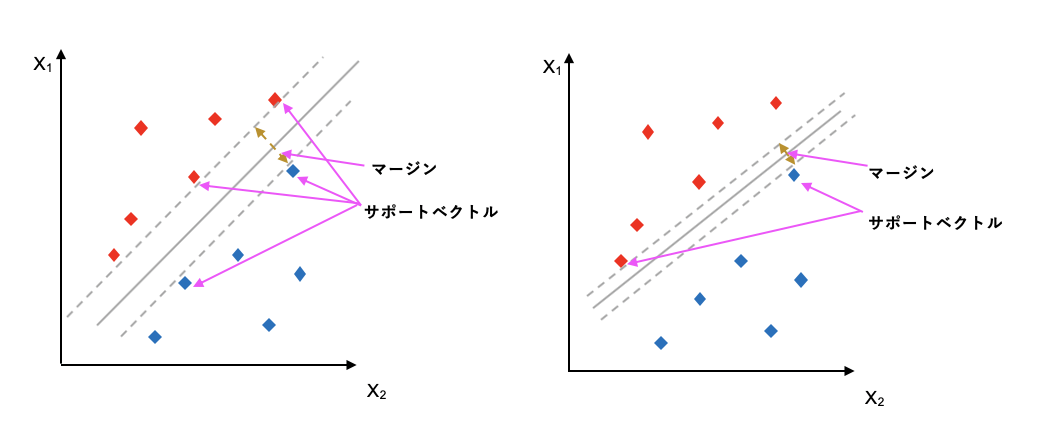
ではこれを数学的に表すとどうでしょう。
まず境界面と直角に交わるベクトルを置きます。

この時、マージンは次の式で表されます。
m = |x_1 - x_2|
= |\frac{(b+1)-(b-1)}{||W||}|
= \frac{2}{||W||}
これを最大化するには、ベクトルのノームの長さ
||W|| = \sqrt{W\cdot W}
を最小化すればいいことが分かります。
min \frac{1}{2}||W||^2 \quad\quad
s.t. \ y_i(w \cdot x_i +b)\geq 1, \quad \forall x_i
要するに「データポイントが制約条件に収まる中でマージンを最小化する」ということです。
ちなみに回帰問題では 1 の代わりに、$\epsilon$ を設定します。この超平面から+/- $\epsilon$までの範囲をepsilon tubeと呼びます。
SVMでは、上に述べたように最小化される関数が評価関数となります。
この評価関数で全データポイントを完璧にクラス分けすることをハードマージンと呼びます。しかし、実際のデータでは、これに完璧に当てはめるのは難しいので、ペナルティーをつけてあげます。これをソフトマージンと言います。最終的な評価関数は次のようになります。
min \frac{1}{2}||W||^2 + C \sum_{i} \zeta_i \quad\quad s.t. \ y_i(w \cdot x_i +b) \geq 1, \quad \forall x_i
このCの値によって、どこまでの誤差を許容範囲とするかが決まります。Cが大きいほど、完璧な分類になります。
カーネル
では次にSVMのカーネルについて説明します。
カーネルとは、「入力されたN次元のデータを高次元に写すことで、境界面を決めるのに使われる関数」です。最初に図で表したように、データによっては入力データの次元だけでは分類できないものが存在します。そのような場合に、次元を変換し、分類できるようにしてくれるのがカーネルです。
代表的なカーネルを紹介します。
線形カーネル
線形カーネルは、同じ入力データを同じ次元に写像します。
K (x,x') = x^T x'
多項式カーネル
多項式カーネルは、入力次元をもとに高次元に写像します。
K^{d,c} (x,x') = (x\cdot x'+c)^d
RBF (radial basis function)
RBFは最もよく使われるカーネル関数です。広範囲のサポートベクターに対応でき、次元は無限となります。
K_\phi(x,x') = e^{-\gamma||x-x'||^2}
他にも様々なカーネルが存在し、SVMではこのカーネルをいかに上手く構築できるかで、モデルの精度が変わります。
先ほどの評価関数をカーネルを使って表すと、
min \frac{1}{2}||W||^2 + C \sum_{i} \zeta_i \quad\quad s.t. \ y_i(w \cdot \phi(x_i) +b)\geq 1, \quad \forall x_i
となります。
この評価関数を満たすWとbは、ラグランジュ未定乗数法を使って次のように解きます。
L(\boldsymbol{w}, b, \boldsymbol{a}) = \frac{1}{2}||w||^2 - \sum_{i=1}a^i[y^i(\boldsymbol{w}^T\boldsymbol{x}^i+b)-1]
a = (a^1, ... , a^N)^T
先ほど制約式にあったものが、目的変数に移動しているのがわかります。
上のラグランジュ関数をwとbで微分し、0とおきます。
w = \sum_{i = 1} a^i y^i x^i
\sum_{i=1}a^iy^i = 0
これを L に代入した関数を最小化する $a^i$ を選択します。
min \frac{1}{2} \sum_{i=1}\sum_{j = 1}a_i a_j y_i y_j \boldsymbol{x}_i^T\boldsymbol{x}_j - \sum_{i=1} a_i
s.t -a^i \leq 0 \quad \forall{i} \quad \sum_{i=1}a^iy^i = 0
最後に求めた $a$を代入し、 wとbを求めます。
w = \sum_{i}a_iy_i\phi(x_i)
b = y_i - \sum_{(x_j, y_j) \in S} a_jy_j(\phi(x_i)\cdot\phi(x_j))
for \quad S = \{(\phi(x_k), y_k)|a_k > 0 \} \quad and \quad (\phi(x_i),y_i \in S)
scikit-learnでSVM
Support Vector Clasification
from sklearn.svm import SVC
model = SVC(kernel = 'linear', random_state = None)
model.fit(x_train, y_train)
y_pred = mode.predict(x_test)
SVCのハイパーパラメター
| パラメター | 概要 | オプション | デフォルト |
|---|---|---|---|
| C | ペナルティ | float | 1.0 |
| kernel | カーネル | linear, poly, rbf, sigmoid | rbf |
| degree | 多項式カーネルの係数 | int | 3 |
| gamma | rbf, poly, sigmoid カーネルの係数 (正則化のようなもの) | float | 'auto' |
| coef0 | カーネル関数の独立項 | float | 0.0 |
| shrinking | heuristicを下げる(計算スピードを調節) | bool | True |
| probability | 予測確率を計算するか | bool | False |
| tol | 終了条件 | float | 1e-3 |
| chase_size | カーネルのキャッシュサイズ(計算スピードを調節) | ||
| class_weight | クラスごとにCを重み付け | None, dict, 'balanced' | None(1) |
| verbose | 途中プロセスの表示 | bool | False |
| max_iter | 最大反復回数 | int | -1 |
| decision_functio_shape | 多クラス分類 | 'ovo'(one vs one) , 'ovr' (one vs rest) | 'ovr' |
| random_state | 確率計算に使われるrandom seed | int, RandomStateのインスタンs u, None | None |
Attributes
| 名前 | 機能 |
|---|---|
| support_ | サポートベクターのインデックス |
| support_vectors_ | サポートベクター |
| n_support_ | 各クラスのサポートベクター数 |
| dual_coef_ | サポートベクターの係数 |
| coef_ | 特徴量の重み |
| intercept_ | decision functionの定数 |
| fit_status | 正しくフィットしたか |
SVRのパラメター
| パラメター | 概要 | オプション | デフォルト |
|---|---|---|---|
| C | ペナルティ | float | 1.0 |
| kernel | カーネル | linear, poly, rbf, sigmoid | rbf |
| degree | 多項式カーネルの係数 | int | 3 |
| gamma | rbf, poly, sigmoid カーネルの係数 | float | 'auto' |
| coef0 | カーネル関数の独立項 | float | 0.0 |
| shrinking | heuristicを下げる(計算スピードを調節) | bool | True |
| tol | 終了条件 | float | 1e-3 |
| epsilon | epsilon-SVRのepsilon-tube | float | 0.1 |
| chase_size | カーネルのキャッシュサイズ(計算スピードを調節) | ||
| class_weight | クラスごとにCを重み付け | None, dict, 'balanced' | None(1) |
| verbose | 途中プロセスの表示 | bool | False |
| max_iter | 最大反復回数 | int | -1 |
Attributes
| 名前 | 機能 |
|---|---|
| support_ | サポートベクターのインデックス |
| support_vectors_ | サポートベクター |
| dual_coef_ | サポートベクターの係数 |
| coef_ | 特徴量の重み |
| intercept_ | decision functionの定数 |
SVM の長所と短所
長所
- 高次元のデータに対応できる。
- 学習データに対し、特徴量が多い場合にも対応できる。
- 外れ値に強い。
- 二項分類など特別なケースにも使える。
短所
- 計算時間がかかる。
- 複数のクラスにまたがる場合上手く対応できない。
- 適切なハイパーパラメターとカーネル関数を選ばないと、精度が悪くなる。


