はじめに
画像のフィルタリングは画像処理の基本であり,ぼかしたり,エッジを出したり,特徴抽出したりすることができます.
OpenCVでは,このフィルタリングに関して多くの機能が提供されています.例えば,以下のチュートリアルで紹介されています.
しかし,逆の処理,つまりぼけたのを復元するための処理はOpenCVには直接用意されてません.
このぼけ除去は,しばしば周波数空間のフィルタとして実現されており,畳み込むフィルタをFFTして,それを除算することで実現できます.これを実現するためには周波数空間で画像処理をする必要があります.
これらのぼけ除去に関するチュートリアルは以下にあります.
- FFTでぼけを除去するチュートリアル
- [FFTでモーションブラーを除去するチュートリアル]
(https://docs.opencv.org/4.0.1/d1/dfd/tutorial_motion_deblur_filter.html)
この記事では,逆に周波数領域のフィルタを使わず,画像ドメインのフィルタでぼけを取ることをやってみます.
画像ドメインでのぼけ除去
画像ドメインでのぼけ除去として代表的なものにLucy-Richardsonアルゴリズムがあります.
MATLABだとdeconvlucyで使えます.(deconvlucy:ヘルプ)
しかし,OpenCVではこの関数が実装されていないため,作っていってみましょう.
Lucy-Richardsonアルゴリズム
アルゴリズムの詳細はググればでてくるため割愛しますが,説明がベイズの定理から始まったりなどでわかりにくいかもしれません.
ここでは実装ベースで説明します.
ここではシンプルにぼけはガウスぼけだと仮定してすすめていきます.
J=G*I
J: ぼけ画像
G: ガウスぼけカーネル
I: 理想画像(これを求める)
*: 畳み込み記号
これを入力ぼけ画像Kから頑張ってIを理想に近づけていきます.
-
まず,ぼけが取れた画像(初期値はぼけた画像でよい)に対してぼけを追加して入力として劣化された過程をシミュレーションします:G*I
-
次に,ぼけた入力画像(K)とぼけをシミュレートした画像(J)の比率を取るために単純に除算します:ratio = K/J
-
そして,その比率をぼかします:gr = G*ratio
-
その比率を入力画像に乗算します:I=K.gr (.は要素積)
-
最後に,入力画像を更新して1に戻ります.繰り返しが十分ならこの画像をぼけ除去として採用します.
コードで書くと以下の通り,非常にシンプルです.
なお,入力として8Uが入って来ることを想定してますが,処理はfloatの精度が無いと復元できないため内部で32Fに変換しています.
void LucyRichardsonGauss(const Mat& src, Mat& dest, const Size ksize, const float sigma, const int iteration)
{
Mat srcf;
Mat destf;
Mat ratio;
src.convertTo(srcf, CV_32FC3);
Mat bdest;
srcf.copyTo(destf, CV_32FC3);
for (int i = 0; i < iteration; i++)
{
GaussianBlur(destf, bdest, ksize, sigma);//ぼけのシミュレーション
divide(srcf, bdest, ratio);
GaussianBlur(ratio, ratio, ksize, sigma);//誤差の分配
multiply(destf, ratio, destf);
}
destf.convertTo(dest, CV_8UC3);
}
もしボケ過程をガウスではなくて,任意のカーネルにしたければ,
ぼけのシミュレーションとコメントしてある場所のGaussianBlurに代えて,filter2Dで自分でカーネルを設定してば良いです.
次に別のアルゴリズムであるIterative Back-Projectionアルゴリズムを説明します.
Iterative Back-Projectionアルゴリズム
超解像で古典的なIterative Back-Projection (IBP)アルゴリズムはぼけ除去にも使われます.
実はこのアルゴリズムは,LucyRichardsonとほぼ同じであり,LucyRichardsonは比率フィードバックしているのに対して,IBPでは差分をフィードバックします.
以下のサンプルコードを見れば処理がほとんど同じであることがわかると思います.
void iterativeBackProjectionDeblur(const Mat& src, Mat& dest, const Size ksize, const float sigma, const float backprojection_sigma, const float lambda, const int iteration, Mat& init)
{
Mat srcf;
Mat destf;
Mat subf;
src.convertTo(srcf, CV_32FC3);
if(init.empty()) src.convertTo(destf, CV_32FC3);
else init.convertTo(destf, CV_32F);
Mat bdest;
for (int i = 0; i < iteration; i++)
{
GaussianBlur(destf, bdest, ksize, sigma);//ぼけのシミュレーション
subtract(srcf, bdest, subf);
GaussianBlur(subf, subf, ksize, backprojection_sigma);//誤差の分配
destf += lambda*subf;
}
destf.convertTo(dest, src.depth());
}
空間フィルタでのフィルタの性能改善
RLやIBPでは,ボケ過程をシミュレートしたフィルタの畳み込みと,誤差の拡散を行う畳み込みを交互に繰り返して行います.
実は誤差を拡散するための畳み込みは,ぼけ過程とは無関係に設定でき,極端な話,ただのコピーでも一応復元します.
ここの誤差の拡散にエッジ保存平滑化フィルタ(バイラテラルフィルタなど)を用いることで性能が上がります.
文献はこちら:
ただし,ジョイントバイラテラルフィルタやガイデットフィルタなどガイド画像が使えるエッジ保存平滑化フィルタを使ってください.単純にbilateralFilterの関数ではガイド画像が使えないためうまくいきません.
これはOpenCVのximgproc moduleにあります."x"なのでcontribです.この前のcontrib送り祭りのときに送られたものではなく,安定してずっとcontribです.
実装は,以下のようなコードになります.
関数jointBilateralFilterは私が作成した関数なのでおそらくxphoto moduleに似た関数があるためそれで代用してください.
void iterativeBackProjectionDeblurBilateral(const cv::Mat& src, cv::Mat& dest, const cv::Size ksize, const float sigma, const float backprojection_sigma_space, const float backprojection_sigma_color, const float lambda, const int iteration, cv::Mat& init)
{
Mat srcf;
Mat bdest;
Mat destf;
Mat subf;
src.convertTo(srcf, CV_32FC3);
if (init.empty()) src.convertTo(destf, CV_32FC3);
else init.convertTo(destf, CV_32FC3);
for (int i = 0; i < iteration; i++)
{
GaussianBlur(destf, bdest, ksize, sigma);
subtract(srcf, bdest, subf);
jointBilateralFilter(subf, destf, subf, ksize, backprojection_sigma_color, backprojection_sigma_space);
destf += ((float)lambda)*subf;
}
destf.convertTo(dest, src.type());
}
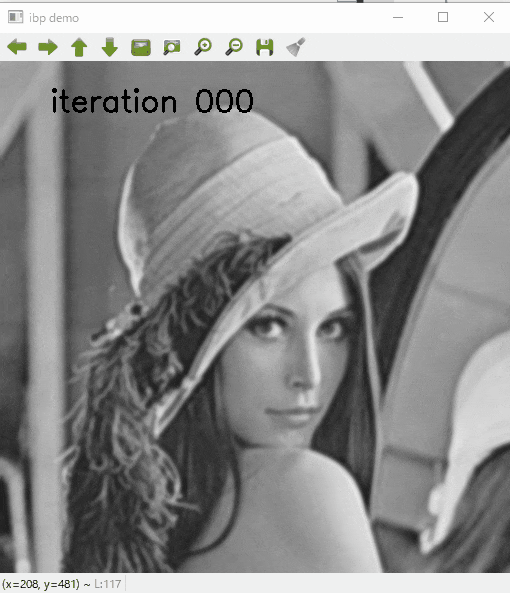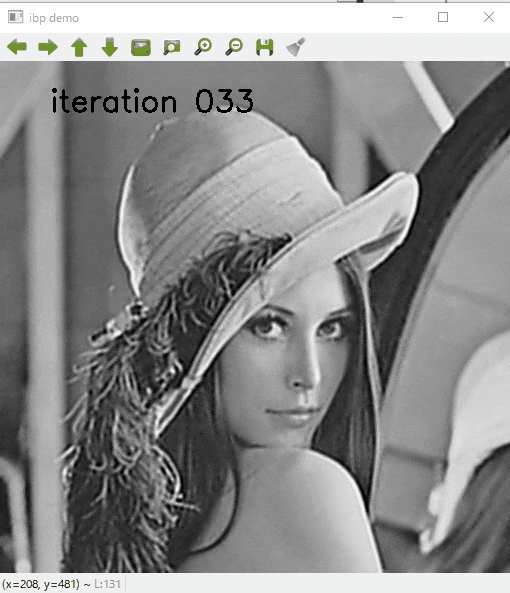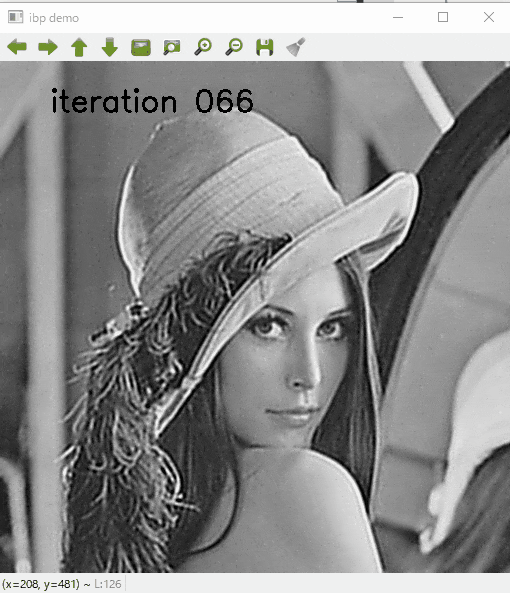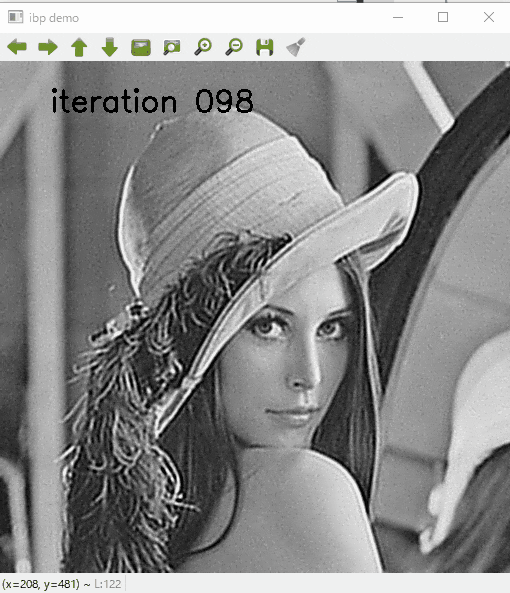
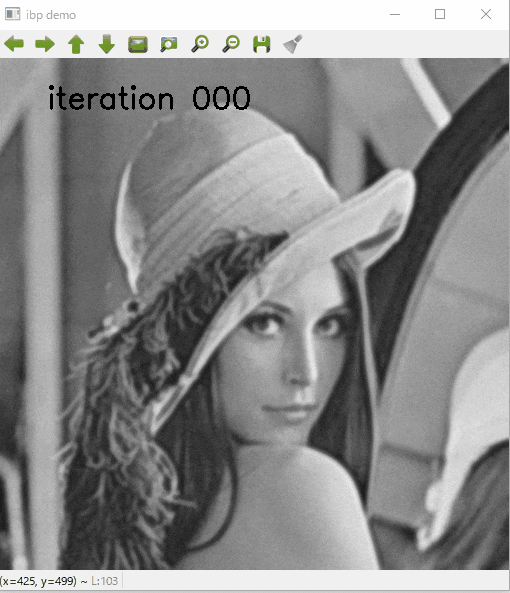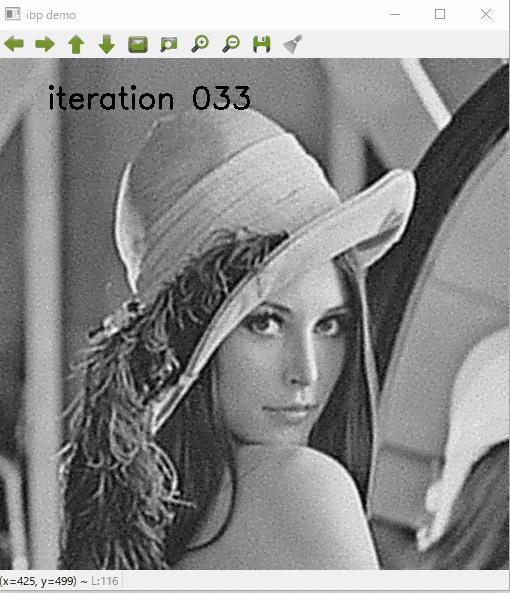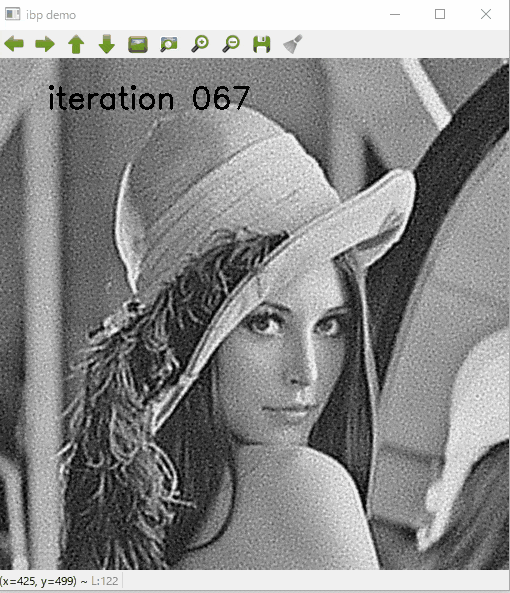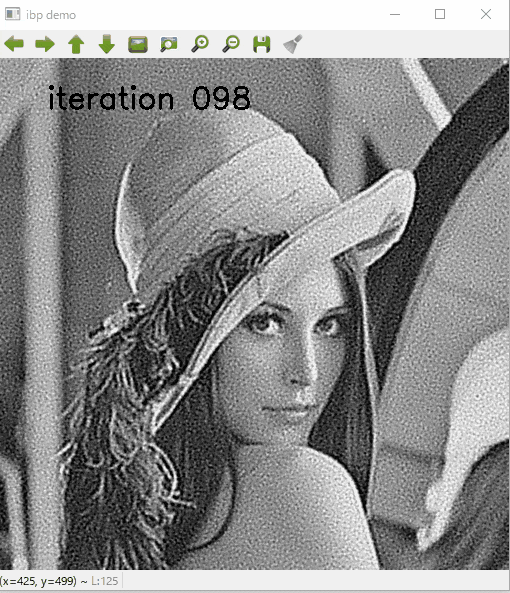
結果
いかにIBPでデブラーした結果を示します.
繰返し処理の途中結果を表示しています.
こんなふうにこのような単純なコードでもボケが復元できます.
しかし実は,このアルゴリズム,ノイズに弱いので,事前にデノイズしてからデブラーしないといけません.
以下の画像はある程度のノイズがのった画像を同じアルゴリズムで復元した結果です.
ぼけ除去は,信号の復元と同時にノイズの増幅を行ってしまうため,ぼけを復元すると同時にノイズも増加していきます.
より高度な手法ならこのあたりもうまく抑えられます.
まとめ
簡単なぼけ除去アルゴリズムについて紹介しました.
あしたは今年のアドベントカレンダー最後の日です!