はじめに
本記事はOpenCV Advent Calendar 2021 の13回目のゆるふわな記事になるはずでした.
ゆるふわ!をコンセプトに書き始めたのに,はじめの「100行で作る」のところしかゆるふわに...
100行で書くってタイトルにつけたらゆるふわになると思っていたときもありました.
バイラテラルフィルタ
導入
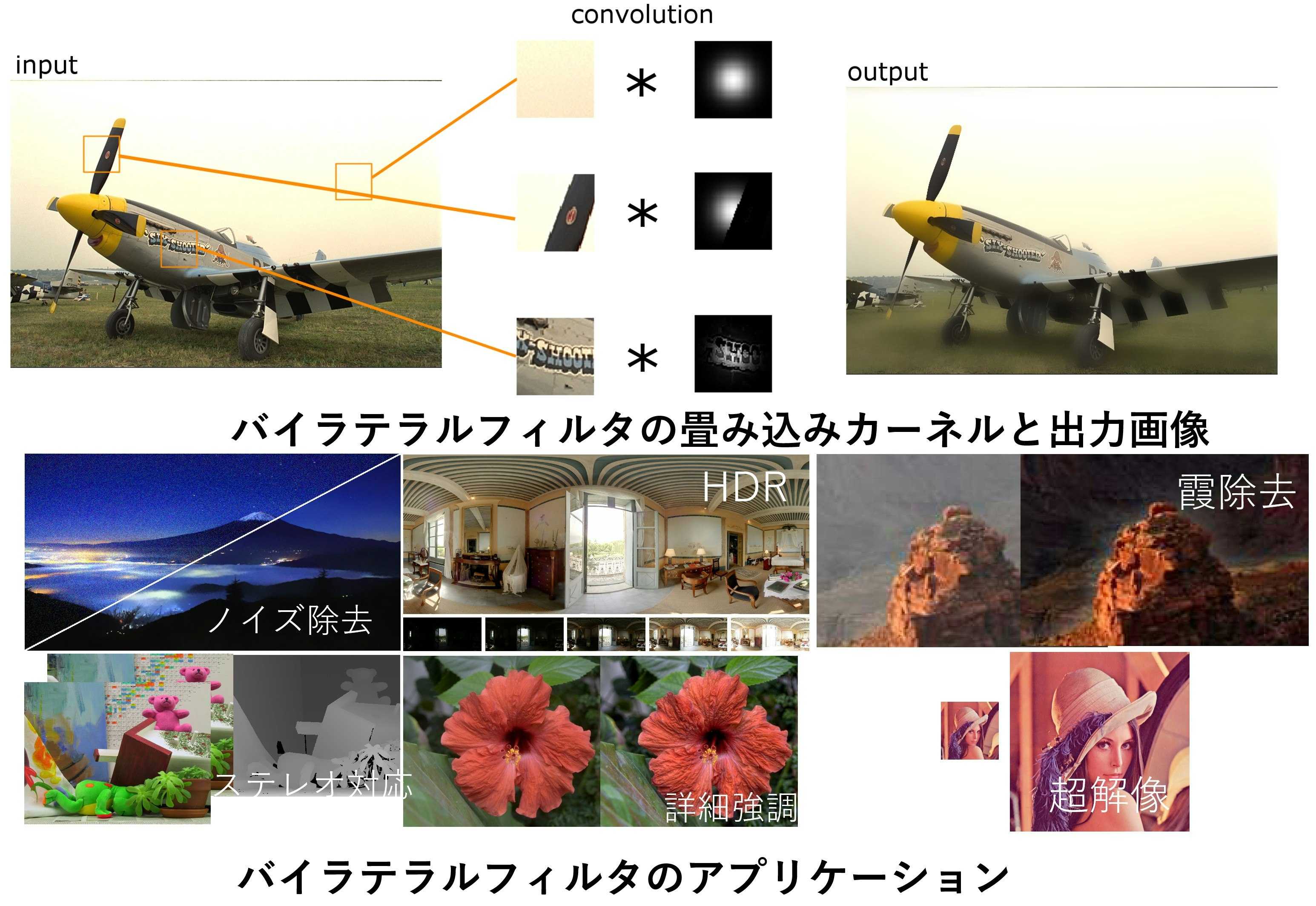
バイラテラルフィルタとは,エッジをまたがないように画像を平らにするフィルタです.
画像のノイズを取ったり,強調をしたり,HDRにつかったり,デプスマップをきれいにしたりといろんなところで使います.
バイラテラルフィルタのOpenCVの関数は下記関数です.
void cv::bilateralFilter (InputArray src, OutputArray dst, int d, double sigmaColor, double sigmaSpace, int borderType = BORDER_DEFAULT );
バイラテラルフィルタの入出力や,そのアプリケーションは下記のイメージになります.
バイラテラルフィルタの定義
バイラテラルフィルタの式は以下で定義されます.
J_p = \frac{\sum_{q \in \mathcal{N}_p} \exp\left(\frac{\|p-q\|_2^2}{-2\sigma_{s}^{2}}\right)\exp\left(\frac{\|I_p-I_q\|_2^2}{-2\sigma_{r}^{2}}\right)I_q}{{\sum_{q \in \mathcal{N}_p} \exp\left(\frac{\|p-q\|_2^2}{-2\sigma_{s}^{2}}\right)\exp(\frac{\|I_p-I_q\|_2^2}{-2\sigma_{r}^{2}})}}
畳み込みカーネルの範囲は集合で$\mathcal{N}_p$で表しています(2重ループで書くのめんどくさい).
$p,q$に対する位置変化に対する重みをスペースカーネル(一個目のexp),$I_p,I_q$に対する輝度変化に対する重みをレンジカーネル(2個目のexp)と呼びます.
もしレンジカーネルの重みが全部1だった場合,ただのガウシアンフィルタです.
(上記画像の空の部分は模様がないのでほぼガウシアンフィルタになっています.)
畳み込みの直径が$D$であれば,$D\times D$のサイズの畳み込みカーネルでコンボリューションする必要があります.
ガウシアンフィルタだったら,どの画素であっても同じ重みで畳み込まれます.
この特性を使いえば,いろんな方法で高速化できます.
しかし,このバイラテラルフィルタは,レンジカーネルがあるため,画素ごとに重みが変わってしまって,高速化は直接的にはできません.
定数時間バイラテラルフィルタの定義
ガウシアンフィルタはいろんな高速化方法があり,古典的な方法ならFFTやセパラブルフィルタで高速化できます.
最近の方法なら,短時間フーリエ変換を使って画素あたり畳み込みの直径に依存しない$O(1)$畳み込みもあります[1,2].
定数時間畳み込みは,ガウシアンフィルタに限らなければ,顔検出に使われるボックスフィルタのインテグラルイメージ(Viola-Jones, 2001)が有名です.
が,初出はこの論文ではありません.ボックフィルタに使うインテグラルイメージを正しく参照するには,下記論文です.私が3歳の時には出てました...
F. C. Crow, “Summed-area tables for texture mapping,” in ACM SIGGRAPH, 1984, pp. 207–212.
さて,定数時間バイラテラルフィルタは,バイラテラルフィルタを複数個のガウシアンフィルタに分解することで,バイラテラルフィルタを定数時間化する戦略です.
ここで,すべての元凶であるレンジカーネルについて考えます.
以下の引数$x,y$を持つガウス分布が,$N$次の変数分離した形で近似できるとします.
つまり,2変数の関数が,1変数の関数の積和で表現できる何かの表現があるとします.
w_r(x,y)=\exp\left(\frac{\|x-y\|_2^2}{-2\sigma^2}\right) \simeq \sum_{n=1}^{N}\xi_n(x)\eta_n(y)
この式を,元のバイラテラルフィルタに代入すると下記になります.
J_p \simeq \frac{\sum_{n=1}^{N}\eta_n(I_p)\sum_{p \in \mathcal{N}} \exp\left(\frac{\|p-q\|_2^2}{-2\sigma_{s}^{2}}\right)\xi_n(I_q) I_q}{\sum_{n=1}^{N}\eta_n(I_p)\sum_{p \in \mathcal{N}} \exp\left(\frac{\|p-q\|_2^2}{-2\sigma_{s}^{2}}\right)\xi_n(I_q)}
このままでは見通しが悪いので,変数を置き換えます.まず,$\xi_n$の関数は,引数$I_q$で値が変換されて何かの画像になるだけで,加えてそれに元の画素値$I_q$をかけたものも画像です.つまり何か画素単位に変換したです.それぞれの画像を$L,M$とおいてあげます.
\xi_n(I_q) I_q=L_{n,q} \quad \xi_n(I_q) = M_{n,q}
J_p \simeq \frac{\sum_{n=1}^{N}\eta_n(I_p)\sum_{p \in \mathcal{N}} \exp\left(\frac{\|p-q\|_2^2}{-2\sigma_{s}^{2}}\right) L_{n,q}}{\sum_{n=1}^{N}\eta_n(I_p)\sum_{p \in \mathcal{N}} \exp\left(\frac{\|p-q\|_2^2}{-2\sigma_{s}^{2}}\right)M_{n,q}}
次に,画像に対する空間コンボリューションの積和の形になります.
畳み込みを$\mathcal{G} *$の形で表現してあげれば以下になります.
J_p = \frac{\sum_{n=1}^{N}\eta_n(I_p){(\mathcal{G} * L_{n,q}})}{\sum_{n=1}^{N}\eta_n(I_p){(\mathcal{G} * M_{n,q}})}
これが意味するのは,バイラテラルフィルタという画素ごとに複雑な計算をしなければいけないものは,実は,ガウシアンフィルタをN回やって積和すれば良いということです.
元のバイラテラルフィルタは,画素あたりオーダーが$O(D^2)$であるのが,定数時間BFで$O(N)$となり,加えて多くの場合で近似次数は畳み込みの直径よりも小さくても構わない$N<D$であるため,相当な高速化が見込めます.
また,$100\times100$といった巨大な畳み込みであっても計算時間は変わりません.
このような形で表現できる変換は多数あり,線形補間[3]やフーリエ変換[4,5],固有値分解[6]や特異値分解[7]などで求めることができます.
ここの例では,一番簡単な線形補間で説明します(いまのところ最も精度が高いのは特異値分解です.)
線形補間をこの形で表現すると下記になります.
簡単に説明するとハットカーネル(三角窓)と,ガウシアンカーネル出力の離散値に分解することになります.
\xi_n (I_p) = w_r(n\tau,Iq)
\eta_n (I_p) = \max (0,1-\frac{|I_p - n\tau|}{\tau})
なお,このアルゴリズムはグレイスケール専用です.
もし入力画像がカラーだった場合,その輝度値の距離(L2ノルム)は,下記となり,簡単に分解できません.
\|\boldsymbol{I_p}-\boldsymbol{I_q}\| = \sqrt{(I_p^r-I_q^r)^2+(I_p^g-I_q^g)^2+(I_p^b-I_q^b)^2}
愚直にやれば,expは指数関数なので,和を積に変えて下記で計算します.
この場合,カラーをそれぞれグレイスケールだと思って,まず青で分解し,その分解したものそれぞれを緑,赤で分解していきます.
つまり,次数Nで分解する場合$N^3$の畳み込みが必要となり,尋常じゃない畳み込み回数が必要となるためカラーで使うのには向いていません.
こういった場合は別のアルゴリズムを使用してください [8].
\exp\left(\frac{\|\boldsymbol{I_p-I_q}\|_2^2}{-2\sigma^2}\right)=\exp\left(\frac{\|I_p^r-I_q^r\|_2^2}{-2\sigma^2}\right)\exp\left(\frac{\|I_p^g-I_q^g\|_2^2}{-2\sigma^2}\right)\exp\left(\frac{\|I_p^b-I_q^b\|_2^2}{-2\sigma^2}\right)
コード
オールマン/BSDのスタイルでちょうど100行です.
この関数では,$\xi$で飛ばすのをsplat,$\eta$で積和を取るところをproductsum関数としています.
動作としては,splatして分母,分子画像を作って,それぞれ畳み込んでその結果をproductsumすることを次数$N$だけ繰り返し,最後に正規化するとバイラテラルフィルタの結果が得られます.
入力画像はCV_8UかCV_32Fのグレイスケール画像です.アルゴリズムがグレイスケールを処理することに特化しています.
出力は,どの入力がCV_8U,CV_32Fに関わらず,CV_32Fで出力します.
カラーに適用する場合は,YUVに変換してYだけに使ったり,RGBそれぞれにかけたりしてください.
OpenCVのガウシアンフィルタは定数時間アルゴリズムではないので,ここでは,定数時間で動くボックスフィルタ(blur関数)で代用しています.
定数時間のガウシアンフィルタは,ここのコードで動きます.
(ヘルプが一切まだないですが,研究室の成果をまとめているプロジェクトであるOpenCPのslnをコンパイルしたら一緒に動きます.cmakeファイルいつか作りたい...)
# include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
class SimpleCBF
{
Mat spnumer, spdenom, src8u, src32, numer, denom;
vector<float> sample;
vector<float> xi;
vector<float> eta;
void initRangeKernel(const float sigma, const int order)
{
sample.resize(order);
xi.resize(256 * order);
eta.resize(256 * order);
const float delta = 255.f / (order - 1);
const float coeff = -1.f / (2.f * sigma * sigma);
for (int n = 0; n < order; n++)
{
sample[n] = delta * n;
}
for (int n = 1; n < order; n++)
{
float* etan = &eta[256 * n];
float* xin = &xi[256 * n];
for (int i = 0; i < 256; i++)
{
const float diff = i - sample[n];
etan[i] = max(0.f, 1.f - abs(diff) / delta);
xin[i] = exp(diff * diff * coeff);
}
}
}
void splat(const Mat& src8u, Mat& numer, Mat& denom, const int n)
{
numer.create(src8u.size(), CV_32F);
denom.create(src8u.size(), CV_32F);
const uchar* s = src8u.ptr<uchar>();
float* dn = numer.ptr<float>();
float* dd = denom.ptr<float>();
const float* xin = &xi[256 * n];
for (int i = 0; i < (int)src8u.total(); i++)
{
dn[i] = xin[s[i]] * float(s[i]);
dd[i] = xin[s[i]];
}
}
void productsum(const Mat& src8u, const Mat& srcNumer, const Mat& srcDenom, Mat& destNumer, Mat& destDenom, const int n)
{
const uchar* s = src8u.ptr<uchar>();
const float* sn = srcNumer.ptr<float>();
const float* sd = srcDenom.ptr<float>();
float* dn = destNumer.ptr<float>();
float* dd = destDenom.ptr<float>();
const float* etan = &eta[256 * n];
const float k_tau = sample[n];
for (int i = 0; i < (int)src8u.total(); i++)
{
dn[i] += etan[s[i]] * sn[i];
dd[i] += etan[s[i]] * sd[i];
}
}
void normalize(const Mat& numer, const Mat& denom, Mat& dst)
{
const float* sn = numer.ptr<float>();
const float* sd = denom.ptr<float>();
float* d = dst.ptr<float>();
for (int i = 0; i < (int)numer.total(); i++)
{
d[i] = sn[i] / sd[i];
}
}
public:
void filter(const Mat& src, Mat& dst, const cv::Size ksize, const float sigma_r, const float sigma_s, const int order, const int borderType = cv::BORDER_DEFAULT)
{
dst.create(src.size(), CV_32F);
numer.create(src.size(), CV_32F);
denom.create(src.size(), CV_32F);
numer.setTo(0);//must be 0 initialized for productsum method
denom.setTo(0);//must be 0 initialized for productsum method
if (src.depth() == CV_8U)
{
src8u = src;
src.convertTo(src32, CV_32F);
}
else
{
src32 = src;
src.convertTo(src8u, CV_8U);
}
initRangeKernel(sigma_r, order);
for (int n = 0; n < order; n++)
{
splat(src8u, spnumer, spdenom, n);
blur(spnumer, spnumer, ksize, Point(-1, -1), borderType);//GaussianBlur(spnumer, spnumer, ksize, sigma_s, sigma_s, borderType);
blur(spdenom, spdenom, ksize, Point(-1, -1), borderType); //GaussianBlur(spdenom, spdenom, ksize, sigma_s, sigma_s, borderType);
productsum(src8u, spnumer, spdenom, numer, denom, n);
}
normalize(numer, denom, dst);
}
};
結果
実行結果を示します.
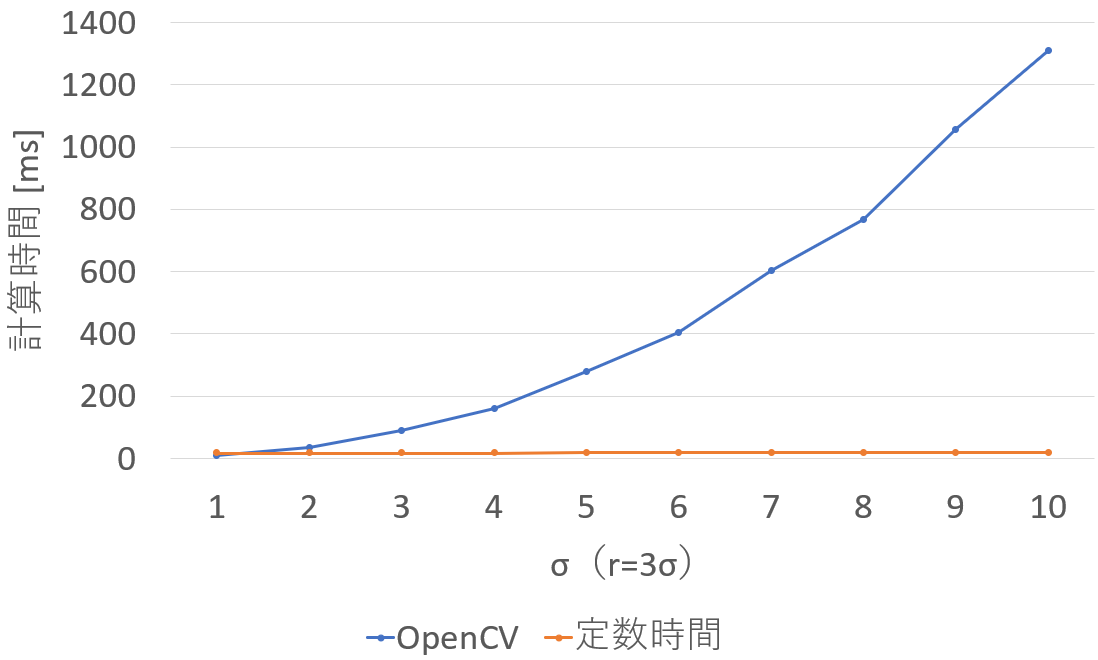
実行環境はCore i7 6700K 4.0GHz 4Core/8Threadです.
畳み込みの半径を$r = 3\sigma_s$として,$\sigma_s$を1~10に増やしていきました.つまり半径3から30の畳み込みをしています.
レンジのパラメータは$\sigma_r=50$,近似次数$N=8$にしました.
近似精度となるPSNRは,ボックスフィルタではなく,ガウシアンフィルタを動かせば59dBで,誤差は全画素の輝度値で±0.5以内にが収まっているはずです(unsingned charでキャストしたらたぶん同じ出力です).
ボックスフィルタを使った場合,フィルタの応答値がだいぶ違うため,PSNRを図る意味は薄いです.
ボックスフィルタx3回くらい重ねがけすると概ねガウシアンフィルタに近づきますですが(矩形カーネル→三角カーネル→三角窓の角が落ちたカーネル),Sliding-DCTベースの定数時間ガウシアンフィルタ使ったほうがいいです.
公開しているコードは,OpenCVのボックスフィルタよりも速く動きます.
これは,OpenCVの実装の問題で,当然最適化したらボックスフィルタのほうが速いですが,おそらくガウシアンフィルタはボックスフィルタの1.1倍もかかりません.
このコードは,並列化していないため,OpenCVのほうも並列化を切っています(cv::setNumThreads(1);で設定しています.).
実行時間は,下記のようになります.定数時間のため,速度は一定です.
定数時間アルゴリズムは18msで動いています.
7x7の畳み込み(この場合の最小ケース)を除いて常時定数時間アルゴリズムのほうが速いです.
出力画像はこんな感じです.
参考文献
[1] T. Otsuka, N. Fukushima, Y. Maeda, K. Sugimoto, and S. Kamata, "Optimization of Sliding-DCT based Gaussian Filtering for Hardware Accelerator," in Proc. International Conference on Visual Communications and Image Processing (VCIP), Dec. 2020.
[2] K. Sugimoto and S. Kamata, “Fast gaussian filter with second-order shift property of dct-5,” in Proc. IEEE International Conference on Image Processing (ICIP), 2013.
[3] F. Durand and J. Dorsey, “Fast bilateral filtering for the display of high-dynamic-range images,” ACM Transactions on
Graphics, vol. 21, no. 3, pp. 257–266, 2002.
[4] K. Sugimoto and S. Kamata, “Compressive bilateral filtering,” IEEE Transactions on Image Processing, vol. 24, no. 11, pp. 3357–3369, 2015.
[5] Y. Sumiya, N. Fukushima, K. Sugimoto, and S. Kamata, “Extending compressive bilateral filtering for arbitrary range kernel,” in Proc. IEEE International Conference on Image Processing (ICIP), 2020.
[6] K. Sugimoto, T. Breckon, and S. Kamata, “Constant-time bilateral filter using spectral decomposition,” in Proc. IEEE International Conference on Image Processing (ICIP), 2016.
[7] K. Sugimoto, N. Fukushima, and S. Kamata, “200 fps constant-time bilateral filter using svd and tiling strategy,” in Proc. IEEE International Conference on Image Processing (ICIP), 2019.
[8] T. Miyamura, N. Fukushima, M. Waqas, K. Sugimoto, and S. Kamata, "Image Tiling for Clustering to Improve Stability of Constant-time Color Bilateral Filtering," in Proc. International Conference on Image Processing (ICIP), Oct. 2020.
まとめ
OpenCVのコードより速いバイラテラルフィルタをアルゴリズムだけで実現しときました.
なお,このコードは,並列化もベクトル化もしていないので,まだまだパフォーマンスは上がります.
また,アルゴリズムももっと良いのがあり,畳み込みの回数を分母と分子で共有して半分にしたり,次数$N$を減らしても精度が高く維持できる方法があったりします.
次回
「10万行でつくる定数時間バイラテラルフィルタ!」
(次回は,永遠に来ないでしょう)
この,定数時間バイラテラルフィルタの内容を研究しており,研究用のコードをカウントすると112,524行になってました.
そりゃインテルコンパイラで最適化すると5分とか10分とかかかると...
100行ではなく,行数1000倍にして最適化すると,512x512程度なら,最近のCPUを使えば1000fps(1ms)は出ます.
E:\Github\Survey-of-ConstantTimeBF\ConstantTimeBF>find /v /c "" *pp
---------- CONSTANTTIMEBF.CPP: 1704
---------- CONSTANTTIMEBFCOLOR.CPP: 1824
---------- CONSTANTTIMEBFCOLOR_NORMALFORM.CPP: 2374
---------- CONSTANTTIMEBFCOLOR_NORMALFORM_TEMPLATE.CPP: 3696
---------- CONSTANTTIMEBFCOLOR_NORMALFORM_TEMPLATE.HPP: 205
---------- CONSTANTTIMEBF_COMPRESSIVE.CPP: 3762
---------- CONSTANTTIMEBF_EVD.CPP: 2803
---------- CONSTANTTIMEBF_INITRANGEKERNEL.CPP: 5770
---------- CONSTANTTIMEBF_LINEAR.CPP: 3583
---------- CONSTANTTIMEBF_NORMALFORM.CPP: 8950
---------- CONSTANTTIMEBF_NORMALFORM_TEMPLATE.CPP: 8723
---------- CONSTANTTIMEBF_NORMALFORM_TEMPLATE.HPP: 255
---------- CONSTANTTIMEBF_POLYNOMIAL.CPP: 2444
---------- CONSTANTTIMEBF_RAISED.CPP: 2930
---------- CONSTANTTIMEBF_RAISEDPOLY.CPP: 1300
---------- CONSTANTTIMEBF_SPLATTINGWITHGF.CPP: 208
---------- CONSTANTTIMEBF_SPLATTINGWITHGF_DCT3.CPP: 12819
---------- CONSTANTTIMEBF_SPLATTINGWITHGF_DCT5.CPP: 9976
---------- CONSTANTTIMEBF_SVD.CPP: 2080
---------- GAUSSIANFILTERAM.CPP: 775
---------- GAUSSIANFILTERDERICHE.CPP: 4013
---------- GAUSSIANFILTERFIRKAHAN.CPP: 327
---------- GAUSSIANFILTERFIROPENCV.CPP: 56
---------- GAUSSIANFILTERFIRSEP2DOPENCV.CPP: 134
---------- GAUSSIANFILTEROPENCV2D.CPP: 135
---------- GAUSSIANFILTERSEPFIR.CPP: 19255
---------- GAUSSIANFILTERVYV.CPP: 4523
---------- PATCHSIMDFUNCTIONS.HPP: 74
---------- SPATIALFILTER.CPP: 1140
---------- SPATIALFILTERBOX.CPP: 44
---------- SPATIALFILTERDCT.CPP: 330
---------- SPATIALFILTERRSLIDINGDCT3_AVX.CPP: 4777
---------- SPATIALFILTERRSLIDINGDCT5_AVX.CPP: 10333
---------- SPATIALFILTERSLIDINGDCT.CPP: 754
---------- SPATIALFILTERSLIDINGDCT1_AVX.CPP: 5783
---------- SPATIALFILTERSLIDINGDCT7_AVX.CPP: 2853
---------- STDAFX.CPP: 6
---------- TIMEDIV.CPP: 199