FM音源についてです。
2オペレータのFM合成
練習
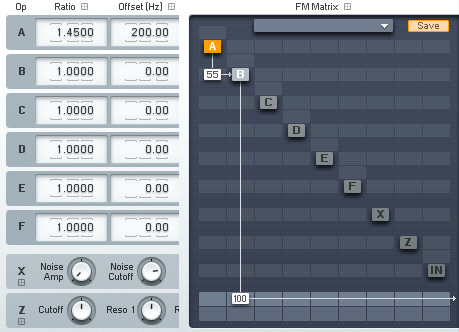
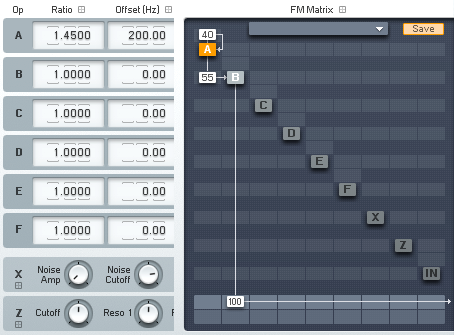
簡単な2オペレータのFM合成について考えてみましょう。今回はNative InstrumentsのFM8を使用します。最初のお題はコレ。
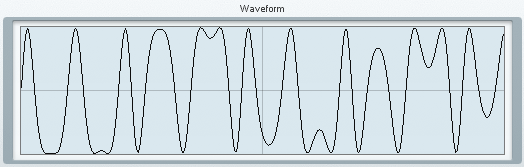
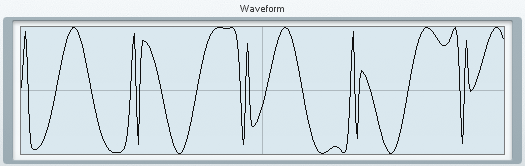
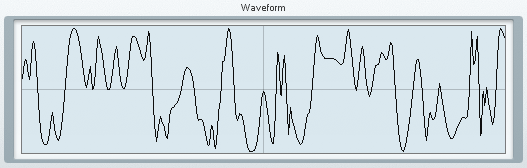
上のように設定すると"Waveform"に次のようなグラフが表示されます。
このグラフの波形が本当に出力されているかと言われると微妙ですが、このグラフの波形を自前で描いてみましょう。数式で書くと次のようなイメージだと思います。
g_2(t_n) = \sin( \, 2\pi ( \, (\alpha_2 f + \beta_2 )t_n
+ m_1 \cdot \sin( \, 2\pi ( \alpha_1 f + \beta_1 )t_n ) \, ) \, )
ここで $f$は基本音の周波数、$ \{ \alpha_1, \alpha_2 \} $はレシオ、$ \{ \beta_1, \beta_2 \} $は オフセット周波数 、$m_1$は モジュレータ振幅 としました。更に次のように変形してみます。
\begin{eqnarray}
c_1 &=& \alpha_1 f + \beta_1 \\
c_2 &=& \alpha_2 f + \beta_2 \\
g_1(t_n) &=& \sin( \, 2\pi c_1 t_n \, ) \\
g_2(t_n) &=& \sin( \, 2\pi ( c_2 t_n
+ m_1 \cdot g_1(t_n) ) \, )
\end{eqnarray}
$\{ c_1, c_2 \}$を キャリア周波数 、更に変調に係わる部分を$g_1$と置きました。揺らす方の$g_1$は モジュレータ で揺らされる方の$g_2$は キャリア と言います。また、モジュレータとキャリアのことをまとめて オペレータ と言ったりします。では実際に計算・・・と行きたいところですが、FMマトリクスに表示されている値と実際の値は異なるようです。調べてみたところ次のような感じでした。
\begin{eqnarray}
m_{ij} &=&
\begin{cases}
u_{ij}^2 \, / \, 9600 \quad (i=j) \\
u_{ij}^2 \, / \, 4800 \quad (i \neq j )
\end{cases} \\
h_j &=& w_j^2 \, / \, 10000
\end{eqnarray}
間違っている可能性大ですが、深入りはしないで先に進みましょう。ではGnuplot用のdatファイルを作成してみます。
import numpy as np
# モジュレータ振幅の変換
def convert_modulation_amplitude(x):
return x*x/4800.0
f = 260.0 # 基本音の周波数[Hz]
fs = 44100.0 # サンプリング周波数[Hz]
a1 = 1.45 # Ratio(オペレータ1)
a2 = 1.0 # Ratio(オペレータ2)
b1 = 200.0 # Offset[Hz](オペレータ1)
b2 = 0.0 # Offset[Hz](オペレータ2)
m12 = convert_modulation_amplitude(55.0) # モジュレータ振幅
c1 = a1*f + b1 # キャリア周波数[Hz](オペレータ1)
c2 = a2*f + b2 # キャリア周波数[Hz](オペレータ2)
dt1 = c1/fs # 刻み間隔[s](オペレータ1)
dt2 = c2/fs # 刻み間隔[s](オペレータ2)
t1 = 0.0 # 時刻(オペレータ1)
t2 = 0.0 # 時刻(オペレータ2)
for _ in range(int(2*fs/f)):
# update operator
g1 = np.sin(2*np.pi*(t1))
g2 = np.sin(2*np.pi*(t2 + m12*g1))
# output
print(g2)
# update time
t1 += dt1
t2 += dt2
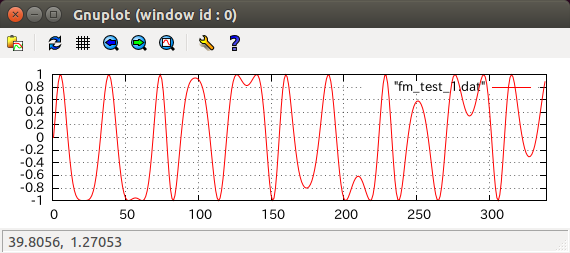
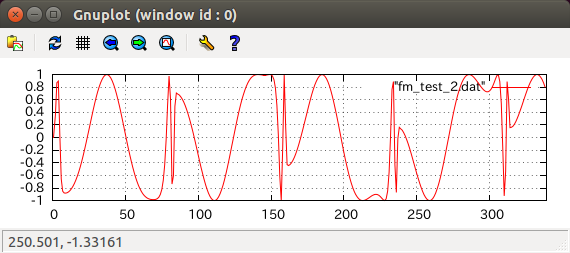
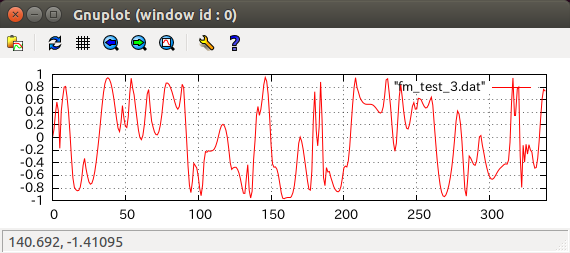
実際にVSTプラグインなどのリアルタイム処理では負荷を軽くするためにsin関数を使わずにウェーブテーブルを使用するなど工夫しますがここでは頑張らないことにします。g2の値をグラフに表示してみましょう。
おお。大体あってそうです。
フィードバッグ
FM合成でよく フィードバック という単語を聞きますが、具体的にはどのような処理を行っているのでしょうか? 次はコレを考えてみましょう。
$g_1(t_n)$はこれから計算しようとしている値なので単純にフィードバックとして使用するのは難しそうです。そうすると1サンプル前の$g_1(t_{n-1})$が使用するのが手っ取り早そうです。
\begin{eqnarray}
g_1(t_n) &=& \sin( \, 2\pi ( c_1 t_n
&+& m_{11} \cdot g_1(t_{n-1} ) ) \, ) \\
g_2(t_n) &=& \sin( \, 2\pi( c_2 t_n
&+& m_{21} \cdot g_1(t_n) ) \, )
\end{eqnarray}
ではdatファイル作成します。
import numpy as np
# モジュレータ振幅の変換
def convert_modulation_amplitude(x):
return x*x/4800.0
# モジュレータ振幅の変換(対角成分)
def convert_modulation_amplitude_diag(x):
return x*x/9600.0
f = 260.0 # 基本音の周波数[Hz]
fs = 44100.0 # サンプリング周波数[Hz]
a1 = 1.45 # Ratio(オペレータ1)
a2 = 1.0 # Ratio(オペレータ2)
b1 = 200.0 # Offset[Hz](オペレータ1)
b2 = 0.0 # Offset[Hz](オペレータ2)
m11 = convert_modulation_amplitude_diag(40.0) # モジュレータ振幅
m12 = convert_modulation_amplitude(55.0) # モジュレータ振幅
c1 = a1*f + b1 # キャリア周波数[Hz](オペレータ1)
c2 = a2*f + b2 # キャリア周波数[Hz](オペレータ2)
dt1 = c1/fs # 刻み間隔[s](オペレータ1)
dt2 = c2/fs # 刻み間隔[s](オペレータ2)
g1 = 0.0 # オペレータ1
t1 = 0.0 # 時刻(オペレータ1)
t2 = 0.0 # 時刻(オペレータ2)
for _ in range(int(2*fs/f)):
# update operator
g1 = np.sin(2*np.pi*(t1 + m11*g1))
g2 = np.sin(2*np.pi*(t2 + m12*g1))
# output
print(g2)
# update time
t1 += dt1
t2 += dt2
$g_2$の値をグラフに表示してみましょう。
今回もまあまあ大丈夫そうですね。
拡張
FM合成の式の拡張を考えてみましょう。
他のオペレータへのフィードバック
フィードバックについてですが、$g_2$のフィードバックというのも考えられそうです。$g_1$のときと同じように1サンプル前の値 $g_2(t_{n-1})$ を使用します。
\begin{eqnarray}
g_1(t_n) &=& \sin( \, 2\pi ( c_1 t_n
&+& m_{11} \cdot g_1(t_{n-1}) ) \, ) \\
g_2(t_n) &=& \sin( \, 2\pi ( c_2 t_n
&+& m_{21} \cdot g_1(t_n) + m_{22} \cdot g_2(t_{n-1}) ) \, )
\end{eqnarray}
ついでに$g_2$ から$g_1$へのフィードバックというのがあっても良さそうですね。
\begin{eqnarray}
g_1(t_n) &=& \sin( \, 2\pi ( c_1 t_n
&+& m_{11} \cdot g_1(t_{n-1} ) &+& m_{12} \cdot g_2(t_{n-1}) ) \, ) \\
g_2(t_n) &=& \sin( \, 2\pi ( c_2 t_n
&+& m_{21} \cdot g_1(t_n) &+& m_{22} \cdot g_2(t_{n-1}) ) \, )
\end{eqnarray}
他のオペレータ値の出力
$g_2$だけでなく$g_1$も出力に使用してみるのもアリかもしれません。$\{ h_1, h_2 \}$をボリューム、$v_n$を出力値とすると次のように表現出来ると思います。
v_n = h_1 \cdot g_1(t_n) + h_2 \cdot g_2(t_n)
FM合成の行列表現
モジュレータ項の統一
$g_1, g_2$ 式をもう一度見てみましょう。
\begin{eqnarray}
g_1(t_n) &=& \sin( \, 2\pi ( c_1 t_n
&+& m_{11} \cdot g_1(t_{n-1} ) &+& m_{12} \cdot g_2(t_{n-1}) ) \, ) \\
g_2(t_n) &=& \sin( \, 2\pi ( c_2 t_n
&+& m_{21} \cdot g_1(t_n) &+& m_{22} \cdot g_2(t_{n-1}) ) \, )
\end{eqnarray}
モジュレータ項の$m_{21} \cdot g_1(t_n)$が仲間外れのような気がします。この時点で$g_1(t_n)$の値は求まっていますので使用して構わないのですが、変調に関しては1サンプル前で計算済みの値を使用するように統一してみます。
\begin{eqnarray}
g_1(t_n) &=& \sin( \, 2\pi ( c_1 t_n
&+& m_{11} \cdot g_1(t_{n-1} ) &+& m_{12} \cdot g_2(t_{n-1}) ) \, ) \\
g_2(t_n) &=& \sin( \, 2\pi ( c_2 t_n
&+& m_{21} \cdot g_1(t_{n-1}) &+& m_{22} \cdot g_2(t_{n-1}) ) \, )
\end{eqnarray}
キャリアとモジュレータのことをオペレータと言いますが、どちらかと言うとオペレータ自身がキャリアになったりモジュレータになったりという表現の方がしっくりくるかもしれません。
行列表現
結局何がしたいのかと言うと、上のように置くことによって次のように変形することが出来ます。
キャリア周波数を・・・
c =
\begin{pmatrix}
c_1 \\
c_2
\end{pmatrix}
=
\begin{pmatrix}
\alpha_1 \\
\alpha_2
\end{pmatrix}
f +
\begin{pmatrix}
\beta_1 \\
\beta_2
\end{pmatrix}
キャリア波形を・・・
\psi(x) = \psi
\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix}
=
\begin{pmatrix}
\sin(2 \pi x_1) \\
\sin(2 \pi x_2)
\end{pmatrix}
モジュレータ振幅を・・・
M =
\begin{pmatrix}
m_{11} & m_{12} \\
m_{21} & m_{22}
\end{pmatrix}
オペレータを・・・
g(t) =
\begin{pmatrix}
g_1(t) \\
g_2(t) \\
\end{pmatrix}
ボリュームを・・・
h =
\begin{pmatrix}
h_1 \\
h_2
\end{pmatrix}
と置けば
\begin{eqnarray}
g(t_n) &=& \psi( \, c t_n + M g(t_{n-1}) \, ) \\
v_n &=& ( \, g(t_n), \, h \, )
\end{eqnarray}
おー、行列とベクトルの計算で表現することが出来ました。FMマトリクスがなぜ"FMマトリクス"と呼ばれている理由が解った気がします。
6オペレータのFM合成
任意のアルゴリズムに対するFM合成
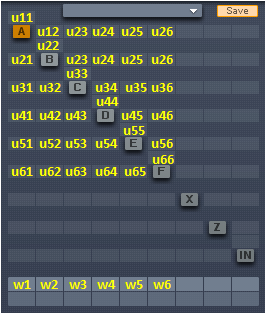
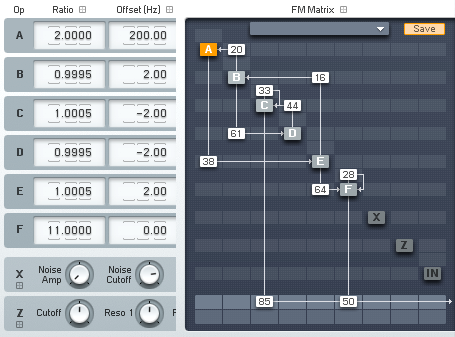
2オペレータで考えてきましたが6オペレータの場合(それ以上でもOK)について考えてみましょう。FM合成の線の繋ぎ方のことを アルゴリズム と言います。アルゴリズムが固定の場合はそれ用に処理を実装するのも良いですが、任意のFMマトリクスに対応するにはどのような実装にすれば良いでしょうか? 先程、FM合成を行列を使って表現しましたが、行列のサイズを2から6にするだけで行けそうな気がします。では適当の値で確認してみましょう。最後のお題はコレ。
実装ですが、Rubyは標準でMatrixクラスとVectorクラスが用意されています。折角なので使ってみます。
import numpy as np
# モジュレータ振幅の変換
def convert_modulation_amplitude(arr):
return np.where(np.eye(arr.shape[0]) != 0, arr*arr/9600.0, arr*arr/4800.0)
# ボリュームの変換
def convert_volume(arr):
return arr*arr/10000.0
f = 260.0 # 基本音の周波数[Hz]
fs = 44100.0 # サンプリング周波数[Hz]
# Ratio
a = np.array([ 2.0000,
0.9995,
1.0005,
0.9995,
1.0005,
11.0000])
# Offset[Hz]
b = np.array([200.00,
2.00,
-2.00,
-2.00,
2.00,
0.00])
# モジュレータ振幅
diplay_fm_mat = np.array([[ 0,20, 0, 0, 0, 0],
[ 0, 0, 0, 0,16, 0],
[ 0, 0,33,44, 0, 0],
[ 0,61, 0, 0, 0, 0],
[38, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0,64,28]])
fm_mat = convert_modulation_amplitude(diplay_fm_mat)
# ボリューム
display_volume = np.array([ 0,
0,
85,
0,
0,
50])
volume = convert_volume(display_volume)
# キャリア周波数[Hz]
c = a*f + b
# キャリア波形
def carrier_waveform(vec):
return np.sin(2*np.pi*vec)
dt = c/fs # 刻み間隔[s]
g = np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0]) # オペレータ
t = np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0]) # 時刻
for _ in range(int(2*fs/f)):
# update operator
g = carrier_waveform(t + np.dot(fm_mat, g))
# output
print(np.dot(g, volume))
# update time
t += dt
で結果は・・・
今回もまあまあ大丈夫ということで。