はじめに
整数FFTを試します。整数FFTは固定小数点FFTという意味ではなく整数から整数への変換なので、逆変換で元に戻すことが可能です。
普通のFFT
Cooley-Tukey型のFFT(Radix-2)について考えます。
Forward FFT
長さ$N$のDFTから考えます。
A_k = \sum_{j=0}^{N-1} a_j W_N^{jk}, \ \ W_N = e^{-2 \pi i/N}
$N$が2で割り切れる場合、添字$k$を偶数と奇数に分けることで2つの長さ$N/2$のDFTに分解することが出来ます。
\begin{eqnarray}
A_{2k} &=& \sum_{j=0}^{N/2-1} (a_j + a_{N/2+j}) W_{N/2}^{jk} \\
A_{2k+1} &=& \sum_{j=0}^{N/2-1} ( \ (a_j - a_{N/2+j}) W_N^j \ ) W_{N/2}^{jk}
\end{eqnarray}
この分解を再帰的に繰り返すことにより計算量が削減出来ます。上の式を正直に効率度外視で擬似コード化します。
import cmath
from itertools import chain
def fft(aa):
n = len(aa)
if(n > 1):
ww = (cmath.exp(-2j*cmath.pi*k/n) for k in range(n//2))
aa1 = fft( [(a1+a2) for a1,a2 in zip(aa,aa[n//2:])] )
aa2 = fft( [(a1-a2)*w for a1,a2,w in zip(aa,aa[n//2:], ww)] )
return list(chain.from_iterable(zip(aa1,aa2)))
else:
return aa
普通のFFTの場合、整数を入力しても(a1-a2)*wの回転因子の乗算により整数ではいられなくなります。整数FFTでは回転因子の乗算結果を整数値に変換かつ逆変換で復元出来るように改造します。但し、回転因子の乗算を非線形演算に置き換えることになるので普通のFFT/DFTが持つ線形性などのいくつかの性質が失われてしまいます。
Inverse FFT
普通のIFFT(逆FFT)は回転因子を逆回転にする方法や、以下のように作成済みのforwardなFFTと複素共役を用いて以下のように作成する方法もあります。
def ifft(aa):
conjugate( fft(conjugate(aa)) ) / len(aa)
また、以下のようにforwardなFFTの逆の手順を踏むことで復元することも出来ます。
import cmath
def ifft(aa):
n = len(aa)
if(n > 1):
ww = (cmath.exp(-2j*cmath.pi*k/n) for k in range(n//2))
aa1 = ifft( aa[0::2] )
aa2 = [a2/w for a2,w in zip(ifft( aa[1::2] ), ww)]
return [(a1+a2)/2 for a1,a2 in zip(aa1,aa2)] + \
[(a1-a2)/2 for a1,a2 in zip(aa1,aa2)]
else:
return aa
整数FFTの逆変換はforwardなFFTの逆の手順を踏む方法を採用します。
準備
整数から整数へ変換するという技術は、ウェーブレット解析の分野で開発された技術が基となっています。
Fast Wavelet Transform
以下のような正規化されていないHaarウェーブレットを用いた分解から考えます。
\begin{eqnarray}
s_{1,0} &=& (s_{0,0} + s_{0,1})/2 \\
d_{1,0} &=& s_{0,1} - s_{0,0}
\end{eqnarray}
2つの値の平均と差だと思っていただいても良いです。$(s_{0,0}, s_{0,1}) \rightarrow (s_{1,0}, d_{1,0})$の変換行列$P$とその逆行列$P^{-1}$は以下になります。
P=
\begin{pmatrix}
1/2 & 1/2 \\
-1 & 1
\end{pmatrix}
, \ \ P^{-1}=
\begin{pmatrix}
1 & -1/2 \\
1 & 1/2
\end{pmatrix}
逆行列から再構成は以下になります。
\begin{eqnarray}
s_{0,0} &=& s_{1,0} - d_{1,0}/2 \\
s_{0,1} &=& s_{1,0} + d_{1,0}/2
\end{eqnarray}
# input
s0_0 = 3
s0_1 = 6
print("[input]")
print("s0_0 =", s0_0)
print("s0_1 =", s0_1)
# decompose
s1_0 = (s0_0 + s0_1)/2.0
d1_0 = s0_1 - s0_0
print("[decompose]")
print("s1_0 =", s1_0)
print("d1_0 =", d1_0)
# reconstruct
s0_0 = s1_0 - d1_0/2.0
s0_1 = s1_0 + d1_0/2.0
print("[reconstruct]")
print("s0_0 =", s0_0)
print("s0_1 =", s0_1)
[input]
s0_0 = 3
s0_1 = 6
[decompose]
s1_0 = 4.5
d1_0 = 3
[reconstruct]
s0_0 = 3.0
s0_1 = 6.0
きちんと復元出来ています。
Lifting Scheme
分解の変換行列を次のようなLifting Stepに分解することを考えます。
\begin{pmatrix}
1 & q_1 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
q_2 & 1
\end{pmatrix}
\begin{pmatrix}
1 & q_3 \\
0 & 1
\end{pmatrix}
\cdots
Haarウェーブレットを用いた分解の行列を以下のように変形します。
P=
\begin{pmatrix}
1 & 1/2 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
-1 & 1
\end{pmatrix}
入力に対して右の行列から適用していくと分解は以下の式になります。
\begin{eqnarray}
d_{1,0} &=& s_{0,1} - s_{0,0} \\
s_{1,0} &=& s_{0,0} + d_{1,0}/2
\end{eqnarray}
分解の逆の手順を踏むことで再構成が出来ます。
\begin{eqnarray}
s_{0,0} &=& s_{1,0} - d_{1,0}/2 \\
s_{0,1} &=& d_{1,0} + s_{0,0}
\end{eqnarray}
# input
s0 = 3
s1 = 6
print("[input]")
print("s0_0 =", s0)
print("s0_1 =", s1)
# decompose
s1 -= s0
s0 += s1/2.0
print("[decompose]")
print("s1_0 =", s0)
print("d1_0 =", s1)
# reconstruct
s0 -= s1/2.0
s1 += s0
print("[reconstruct]")
print("s0_0 =", s0)
print("s0_1 =", s1)
[input]
s0_0 = 3
s0_1 = 6
[decompose]
s1_0 = 4.5
d1_0 = 3
[reconstruct]
s0_0 = 3.0
s0_1 = 6.0
きちんと復元出来ています。
Integer Lifting
分解結果を整数化するため、Lifting Schemeでの$d_{1,0}/2$の小数部分を切り捨てます。
分解:
\begin{eqnarray}
d_{1,0} &=& s_{0,1} - s_{0,0} \\
s_{1,0} &=& s_{0,0} + \lfloor d_{1,0}/2 \rfloor
\end{eqnarray}
再構成:
\begin{eqnarray}
s_{0,0} &=& s_{1,0} - \lfloor d_{1,0}/2 \rfloor \\
s_{0,1} &=& d_{1,0} + s_{0,0}
\end{eqnarray}
切り捨て処理により、分解・再構成が線形な演算ではなくなってしまいましたが、再構成で復元できることがわかります。
# coding: utf-8
# input
s0 = 3
s1 = 6
print("[input]")
print("s0_0 =", s0)
print("s0_1 =", s1)
# decompose
s1 -= s0
s0 += int(s1/2.0)
print("[decompose]")
print("s1_0 =", s0)
print("d1_0 =", s1)
# reconstruct
s0 -= int(s1/2.0)
s1 += s0
print("[reconstruct]")
print("s0_0 =", s0)
print("s0_1 =", s1)
[input]
s0_0 = 3
s0_1 = 6
[decompose]
s1_0 = 4
d1_0 = 3
[reconstruct]
s0_0 = 3
s0_1 = 6
整数への変換方法ですが、切り上げや四捨五入でも復元には問題ありません(このテストコードではint関数で整数に変換しています)。
FFT(Lifting Scheme)
回転因子$W_\theta$のLifting Stepに分解を考えます。
W_\theta=
\begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{pmatrix}
回転角度に応じて2種類を用意します。
タイプA:
W_\theta=
\begin{pmatrix}
1 & \frac{c-1}{s} \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
s & 1
\end{pmatrix}
\begin{pmatrix}
1 & \frac{c-1}{s} \\
0 & 1
\end{pmatrix}
タイプB:
W_\theta=-
\begin{pmatrix}
1 & \frac{c+1}{s} \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
-s & 1
\end{pmatrix}
\begin{pmatrix}
1 & \frac{c+1}{s} \\
0 & 1
\end{pmatrix}
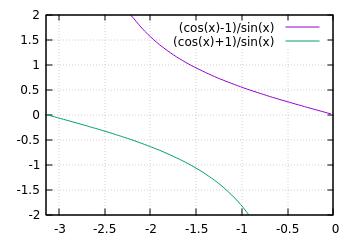
Lifting係数の絶対値が大きくなりすぎると整数型の範囲を超えてしまう可能性があります。$-\pi/2 \le \theta \lt 0 $の場合はタイプA、$-\pi \lt \theta \le -\pi/2 $の場合はタイプBを使用してLifting係数を-1から1の間に収まるようにします。
import cmath
from itertools import chain
def fft_lift(aa):
def lift(x,w):
(c, s) = (w.real, w.imag)
a = [x.real, x.imag]
if(-1.0e-10 < s < 1.0e-10):
pass
elif(c >= 0.0):
a[0] += a[1]*(c-1)/s
a[1] += a[0]*s
a[0] += a[1]*(c-1)/s
else:
a[0] += a[1]*(c+1)/s
a[1] += a[0]*(-s)
a[0] += a[1]*(c+1)/s
a[0] *= -1
a[1] *= -1
return complex(a[0], a[1])
n = len(aa)
if(n > 1):
ww = (cmath.exp(-2j*cmath.pi*k/n) for k in range(n//2))
aa1 = fft_lift( [(a1+a2) for a1,a2 in zip(aa,aa[n//2:])] )
aa2 = fft_lift( [lift(a1-a2,w) for a1,a2,w in zip(aa,aa[n//2:], ww)] )
return list(chain.from_iterable(zip(aa1,aa2)))
else:
return aa
def ifft_lift(aa):
def ilift(x,w):
(c, s) = (w.real, w.imag)
a = [x.real, x.imag]
if( -1.0e-10 < s < 1.0e-10 ):
pass
elif( c >= 0.0):
a[0] -= a[1]*(c-1)/s
a[1] -= a[0]*s
a[0] -= a[1]*(c-1)/s
else:
a[0] *= -1
a[1] *= -1
a[0] -= a[1]*(c+1)/s
a[1] -= a[0]*(-s)
a[0] -= a[1]*(c+1)/s
return complex(a[0], a[1])
n = len(aa)
if(n > 1):
ww = (cmath.exp(-2j*cmath.pi*k/n) for k in range(n//2))
aa1 = ifft_lift( aa[0::2] )
aa2 = [ilift(a2, w) for a2,w in zip(ifft_lift( aa[1::2] ), ww)]
return [(a1+a2)/2 for a1,a2 in zip(aa1,aa2)] + \
[(a1-a2)/2 for a1,a2 in zip(aa1,aa2)]
else:
return aa
このソースコード自体には何もメリットはありません。
整数FFT
Liftingの結果を整数化すれば整数FFTの完成です。
import cmath
from itertools import chain
def int_fft(aa):
def int_lift(x,w):
(c, s) = (w.real, w.imag)
a = [x.real, x.imag]
if(-1.0e-10 < s < 1.0e-10):
pass
elif(c >= 0.0):
a[0] += int(a[1]*(c-1)/s)
a[1] += int(a[0]*s)
a[0] += int(a[1]*(c-1)/s)
else:
a[0] += int(a[1]*(c+1)/s)
a[1] += int(a[0]*(-s))
a[0] += int(a[1]*(c+1)/s)
a[0] *= -1
a[1] *= -1
return complex(a[0], a[1])
n = len(aa)
if(n > 1):
ww = (cmath.exp(-2j*cmath.pi*k/n) for k in range(n//2))
aa1 = int_fft( [(a1+a2) for a1,a2 in zip(aa,aa[n//2:])] )
aa2 = int_fft( [int_lift(a1-a2,w) for a1,a2,w in zip(aa,aa[n//2:], ww)] )
return list(chain.from_iterable(zip(aa1,aa2)))
else:
return aa
def int_ifft(aa):
def int_ilift(x,w):
(c, s) = (w.real, w.imag)
a = [x.real, x.imag]
if( -1.0e-10 < s < 1.0e-10 ):
pass
elif( c >= 0.0):
a[0] -= int(a[1]*(c-1)/s)
a[1] -= int(a[0]*s)
a[0] -= int(a[1]*(c-1)/s)
else:
a[0] *= -1
a[1] *= -1
a[0] -= int(a[1]*(c+1)/s)
a[1] -= int(a[0]*(-s))
a[0] -= int(a[1]*(c+1)/s)
return complex(a[0], a[1])
n = len(aa)
if(n > 1):
ww = (cmath.exp(-2j*cmath.pi*k/n) for k in range(n//2))
aa1 = int_ifft( aa[0::2] )
aa2 = [int_ilift(a2, w) for a2,w in zip(int_ifft( aa[1::2] ), ww)]
return [(a1+a2)/2 for a1,a2 in zip(aa1,aa2)] + \
[(a1-a2)/2 for a1,a2 in zip(aa1,aa2)]
else:
return aa
今回はRadix-2で試しましたが、Mixed-RadixやSplit-Radixの場合で結果が変わるかもしれません。おしまい。