fastersinというsin関数の高速版があるのを知り、面白そうだったのでちょっと手を加えてアレンジしました。
fastapprox
fastapproxは三角関数や指数関数などを高速で計算するためのC言語で書かれたライブラリです。例えばfastersinというsin関数の高速版は以下のようになっています。
static inline float
fastersin (float x)
{
static const float fouroverpi = 1.2732395447351627f;
static const float fouroverpisq = 0.40528473456935109f;
static const float q = 0.77633023248007499f;
union { float f; uint32_t i; } p = { 0.22308510060189463f };
union { float f; uint32_t i; } vx = { x };
uint32_t sign = vx.i & 0x80000000;
vx.i &= 0x7FFFFFFF;
float qpprox = fouroverpi * x - fouroverpisq * x * vx.f;
p.i |= sign;
return qpprox * (q + p.f * qpprox);
}
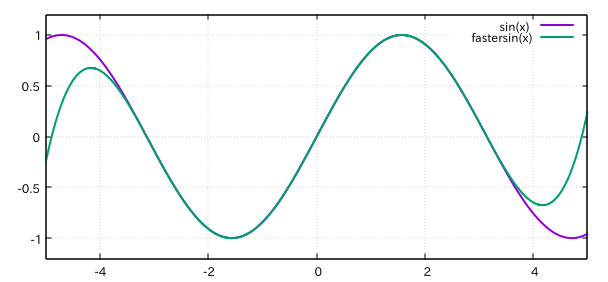
標準ライブラリのsinf関数より2〜3倍速いかなといった感じです。関数をプロットします。
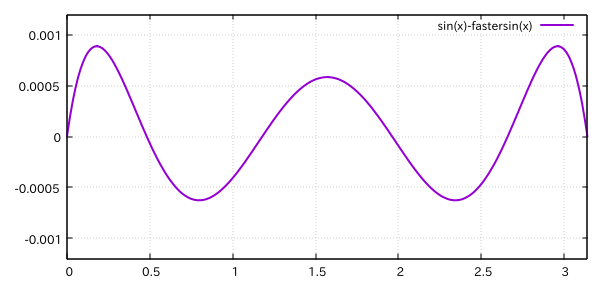
引数は$[-\pi, \pi]$の範囲で渡す必要があります。$[0,\pi]$での誤差もプロットします。
このグラフを見たとき、もう少し頑張れるんじゃないかと思いました。今回はアルゴリズムを変えることなく先頭で宣言されている4つの定数を調整することで誤差を減らしていきます。
最良近似多項式
$f(x)$は区間$[t_0,t_1]$で連続な関数でそれを近似する$n$次多項式を
f_n(x)=\sum_{k=0}^n a_k x^k
とします。$n$を固定したときに
\max_{t_0<x<t_1} |f(x)-f_n(x)|
を最小にするような多項式を最良近似多項式といいます。最良近似多項式は次のような性質を持っています。
$f_n(x)$が最良近似多項式であるための必要十分条件は、誤差関数$\epsilon(x)$を
\epsilon(x) = f(x)-f_n(x)と置いたとき、$|\epsilon(x)|$が区間$[t_0,t_1]$で少なくとも$n+2$点で等しい最大値をとり、最大値における$\epsilon(x)$の符号が交互に並んでいることである。
fastersinは絶対値最大誤差的にもう少し頑張れる気がしますね。
Remez algorithm
Remez algorithmを用いてsin関数を多項式で近似します。アルゴリズムは次のようになっています。
step1. ある区間上に$n+2$個の検査点$x_0, \cdots x_{n+1}$を適当に用意する
step2. 検査点での誤差関数$\epsilon(x)$の絶対値が等しくかつ誤差の符号が交互に並ぶような多項式$f_n(x)$の係数$a_0, \cdots, a_n$と誤差$d$を求め、多項式を更新する
step3. 誤差関数$\epsilon(x)$の絶対値が最大となる$n+2$個の点$x_0, \cdots x_{n+1}$を求め、検査点を更新する
step4. 検査点での誤差関数$\epsilon(x)$の絶対値が等しくかつ誤差の符号が交互に並んでいれば終了し、そうでなければstep2へ戻る
計算
実際に最良近似多項式の係数を計算します。言語はPythonでライブラリはSympyとmpmathを使用します。
準備
オリジナルfastersinを$x$の多項式に展開します。
# -*- coding: utf-8 -*-
import sympy
if __name__ == '__main__':
qpprox = sympy.sympify('s0 * x - s1 * x * x')
fastersin = sympy.sympify('qpprox * (s2 + s3 * qpprox)').subs({'qpprox':qpprox}).expand()
print(fastersin)
expr = {'s0': 1.2732395447351627, # fouroverpi
's1': 0.40528473456935109, # fouroverpisq
's2': 0.77633023248007499, # p
's3': 0.22308510060189463} # q
print(fastersin.subs(expr))
s0**2*s3*x**2 - 2*s0*s1*s3*x**3 + s0*s2*x + s1**2*s3*x**4 - s1*s2*x**2
0.0366430029450163*x**4 - 0.230234777715065*x**3 + 0.0470171509264136*x**2 + 0.988454351767074*x
この多項式の係数はRemez algorithmの初期値として使用します。実はここで問題がありまして、4つの変数fouroverpi,fouroverpisq,p,qを頑張って調整しても定数項は0にしかなりません。
Remez
定数項が0という縛りがありますがRemez algorithmで最良近似多項式を計算します。ライブラリが無いか探しましたが、見つからなかったので諦めて実装します。
# -*- coding: utf-8 -*-
import math, numpy, mpmath
# Remez algorithm --main--
def remez(poly):
# Remez algorithm --step1--
check_points = update_maximum_error_points(poly)
for iteration in range(1, 100):
# Remez algorithm --step2--
poly, d = update_polynomial_coefficients(check_points)
# Remez algorithm --step3--
check_points = update_maximum_error_points(poly)
# Remez algorithm --step4--
if check_convergence(poly, check_points):
return poly, d, iteration
else:
raise Exception('[ERROR]Remez algorithm failed')
# Remez algorithm --step2--
def update_polynomial_coefficients(check_points):
assert len(check_points) == 4+2
# 検査点x[0]=0では誤差が0、それ以外の検査点では誤差dが交互に反転するような条件を課す
mat_A = [[x**4,x**3,x**2,x,1, (0 if k==0 else (-1)**k)] for k,x in enumerate(check_points)]
vec_b = [mpmath.sin(x) for x in check_points]
# 連立方程式を解いて多項式を更新する
u = mpmath.lu_solve(mat_A, vec_b)
return u[:5], mpmath.fabs(u[5])
# Remez algorithm --step3--
def update_maximum_error_points(poly):
# 誤差関数を微分したもの
df = lambda x:mpmath.polyval(poly, x, derivative=True)[1] - mpmath.cos(x)
# エレガントな方法ではないが極値点がありそうなところに辺りをつける
intervals = numpy.linspace(0.0, math.pi, 100)
coarse_roots = [p0 for p0, p1 in zip(intervals, intervals[1:]) if df(p0)*df(p1) <= 0.0]
# 全ての極値点を計算する
extreme_points = [mpmath.findroot(df, x) for x in coarse_roots]
assert len(extreme_points) == 5
# 極値点だけでは足らないのでx=0も検査点として追加する
return [mpmath.mpf(0.0)] + extreme_points
# Remez algorithm --step4--
def check_convergence(poly, check_points):
# 誤差関数
ef = lambda x:mpmath.polyval(poly, x) - mpmath.sin(x)
# x[0]=0を除く検査点の誤差が交互に反転しているかをチェックする
err = numpy.var([ef(x)*(-1)**k for k,x in enumerate(check_points[1:])])
return err < 1.0e-20
if __name__ == '__main__':
print('Remez algorithm... ', end='')
# 初期値としてオリジナルfastersinの多項式を利用する
init_poly = [0.0366430029450163, # a4
-0.230234777715065, # a3
0.0470171509264136, # a2
0.988454351767074, # a1
0.0] # a0
# Remez algorithmで最良近似多項式を計算する
poly, d, iteration= remez(init_poly)
print('success')
# 反復回数
print('iteration:', iteration)
# 最良近似多項式の係数
for k,a in enumerate(reversed(poly)):
print('a%d:'% k, a)
# 誤差d
print('d :', d)
Remez algorithm... success
iteration: 3
a0: 0.0
a1: 0.989715113217385
a2: 0.0447710993902034
a3: -0.229060380582229
a4: 0.0364560918361726
d : 0.000732394766512533
最適化
最後にオリジナルfastersinのアルゴリズムが適用出来るように展開した式を元に戻します。4つの変数を未知とする非線形の方程式を作成して近似解を求めます。
# -*- coding: utf-8 -*-
import mpmath
if __name__ == '__main__':
print('optimize... ', end='')
# 誤差関数
f = lambda s0,s1,s2,s3: \
[s0*s2 - 0.989715113217385, # a1
s0**2*s3 - s1*s2 - 0.0447710993902034, # a2
-2*s0*s1*s3 + 0.229060380582229, # a3
s1**2*s3 - 0.0364560918361726] # a4
# 初期値としてオリジナルfastersinの定数を利用する
initial = [1.2732395447351627, # fouroverpi
0.40528473456935109, # fouroverpisq
0.77633023248007499, # p
0.22308510060189463] # q
ss = mpmath.findroot(f, initial, tol=1.0e-18)
print('success')
for k,s in enumerate(ss):
print('s%d:' % k, s)
optimize... success
s0: 1.2732572472526
s1: 0.405290369455662
s2: 0.777309624389905
s3: 0.221941001052417
改良版fastersin
4つの定数を置き換えたら完成です。
static inline float
remez_sin (float x)
{
static const float s0 = 1.2732572472526f;
static const float s1 = 0.405290369455662f;
static const float s2 = 0.777309624389905f;
union { float f; uint32_t i; } s3 = { 0.221941001052417f };
union { float f; uint32_t i; } vx = { x };
uint32_t sign = vx.i & 0x80000000;
vx.i &= 0x7FFFFFFF;
float qpprox = s0 * x - s1 * x * vx.f;
s3.i |= sign;
return qpprox * (s2 + s3.f * qpprox);
}
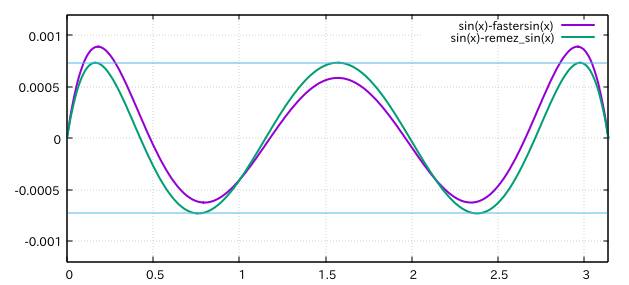
絶対値最大誤差は小さくなりましたが、二乗平均誤差的にはオリジナルfastersinに負けてる気がします。