連立一次方程式の解き方

　連立一次方程式の近似解を求めます。

使用するライブラリ

　Pythonの疎行列ライブラリ scipy.sparse を使用します。連立一次方程式を解くための関数も用意されていますが、そちらは使用せずに自前で実装します。

連立一次方程式

　$x$を未知とする連立一次方程式の近似解を反復法で求めます。

Ax=b

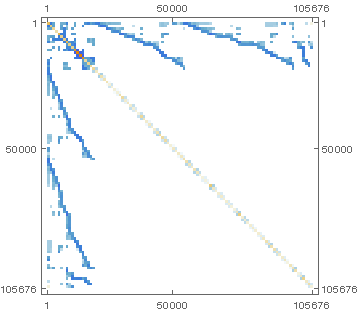
　行列$A$とベクトル$b$は The University of Florida Sparse Matrix Collection からお借りします。

　Matrix: Hamm/hcircuit

http://www.cise.ufl.edu/research/sparse/matrices/Hamm/hcircuit.html

Matrix properties
number of rows	105,676
number of columns	105,676
nonzeros	513,072
type	real
structure	unsymmetric

MatrixMarketフォーマット

　行列の情報を記述するフォーマットは何種類かありますが今回は MatrixMarketフォーマットを使用します。拡張子はプレーンなテキスト形式の"mtx"とテキスト形式をgzip圧縮した"mtx.gz"があります。

行列情報の取得

　行列の情報はscipy.io.mminfo 関数で取得します。

scipy_io_mminfo.py

import scipy.io
print 'A:', scipy.io.mminfo('hcircuit.mtx.gz')
print 'b:', scipy.io.mminfo('hcircuit_b.mtx.gz')

実行結果

A: (105676, 105676, 513072, 'coordinate', 'real', 'general')
b: (105676, 1, 105676, 'array', 'real', 'general')

nonzero要素の読み込み

　nonzero要素の読み込みは scipy.io.mmread 関数で行います。行列はCSR形式、列ベクトルは配列に変換しておきます。

nonzero要素の読み込み

A = scipy.io.mmread('hcircuit.mtx.gz').tocsr()
b = scipy.io.mmread('hcircuit_b.mtx.gz')[:,0]

BiCGStab法

　scipy.sparseライブラリには非対称行列の連立一次方程式を解くための関数がいくつか用意されていますが自前で実装します。今回はBiCGStab(Bi-conjugate gradient stabilized method、安定化双共役勾配法)で試します。ガウスの消去法で行うような行列の基本変形が不要なのが利点です。ちなみにBiCGStab法はscipy.sparse.linalg.bicgstabで既に用意されています。

\begin{eqnarray}
1.&& \ \ \mbox{Compute} \ \ r_0 = b - Ax_0, \ \ r^*_0 \ \ \mbox{arbitary} \\
2.&& \ \ p_0 = r_0 \\
3.&& \ \ \mbox{For} \ \ j = 0,1, \ldots , \mbox{until convergence, Do} \\
4.&& \ \ \ \ \ \ \alpha_j = (r_j, r^*_0) / (Ap_j, r^*_0) \\
5.&& \ \ \ \ \ \ s_j = r_j - \alpha_j Ap_j \\
6.&& \ \ \ \ \ \ \omega_j = (As_j,s_j)/(As_j,As_j) \\
7.&& \ \ \ \ \ \ x_{j+1} = x_j + \alpha_j p_j + \omega_j s_j \\
8.&& \ \ \ \ \ \ r_{j+1} = s_j - \omega_j As_j \\
9.&& \ \ \ \ \ \ \beta_j = \frac{(r_{j+1}, r^*_0)}{(r_j, r^*_0)} \times \frac{\alpha_j}{\omega_j} \\
10.&& \ \ \ \ \ \ p_{j+1} = r_{j+1} + \beta_j (p_j - \omega_j Ap_j) \\
11.&& \ \ \mbox{EndDo}
\end{eqnarray}

bicgstab.py

# -*- coding: utf-8 -*-
import scipy.io, numpy as np, numpy.linalg as nl

name = 'hcircuit'
eps = 1.0e-3

# read matrix and vector
print '#A:', scipy.io.mminfo(name + '.mtx.gz')
print '#b:', scipy.io.mminfo(name + '_b.mtx.gz')
A = scipy.io.mmread(name + '.mtx.gz').tocsr()
b = scipy.io.mmread(name + '_b.mtx.gz')[:,0]
print '#bicgstab start'

# initialize
x_j = np.zeros(b.size)
r_j = r_0 = p_j = b - A.dot(x_j)
r_0_norm = nl.norm(r_0)

# start
for j in range(1, 100001):
    Ap = A.dot(p_j)
    t = np.dot(r_j,r_0)
    a = t/np.dot(Ap,r_0)
    s = r_j - a*Ap
    As = A.dot(s)
    w = np.dot(As,s)/np.dot(As,As)
    x_j = x_j + a*p_j + w*s
    r_j = s - w*As
    c = np.dot(r_j,r_0)/t*a/w
    p_j = r_j + c*(p_j - w*Ap)

    #convergence test
    #print nl.norm(r_j)/r_0_norm
    if np.dot(r_j,r_j) < eps*eps*r_0_norm*r_0_norm:
        print '#number of iterations:', j
        print '#relative residual: %e' % (nl.norm(r_j)/r_0_norm)
        print '#relative error:    %e' % (nl.norm(b-A.dot(x_j))/r_0_norm)
        break
else:
    print 'do not converge!'

実行結果

実行結果

#A: (105676, 105676, 513072, 'coordinate', 'real', 'general')
#b: (105676, 1, 105676, 'array', 'real', 'general')
#bicgstab start
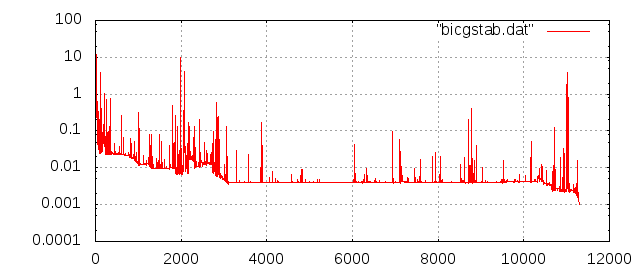
#number of iterations: 11290
#relative residual: 9.812614e-04
#relative error:    9.812614e-04

解法	反復回数	相対残差	相対誤差
BiCGStab	11290	9.812614e-04	9.812614e-04

　反復回数は解く問題や打ち切り誤差に依存します。今回は相対残差 $||r_j||/||r_0||$ が$10^{-3}$未満で反復を打ち切りました。残差$r_j$と誤差$(b-Ax_j)$は解析的には一致しますが上記のロジックでは残差を$r_j = b - Ax_j$で更新しない（打ち切り判定のためだけに$Ax_j$の計算を行いたくない）ため残差$r_j$に計算誤差が蓄積することがあります。

• ソースコード

参考文献

• Yousef Saad, Iterative methods for sparse linear systems (2nd edition)