BLIT合成の導出と実装について

　ノコギリ波のBLIT合成の導出と実装についてです。

BLIT合成の導出

総和計算外し

　BLIT合成のあの式、出所は何処なんでしょうか？ 実は 加算合成方式 すなわち フーリエ級数 が基となっています。ノコギリ波のフーリエ級数を次に示します。

g_N(x) = \frac{2}{\pi} \sum_{k=1}^N \frac{\sin(kx)}{k}

　この式からどうにかして総和計算の（$\sum$）を取り外せないでしょうか？ 分母の $k$ があると厳しそうです。そこで唐突ですが $x$ で微分してみます。

\left( \sum_{k=1}^N \frac{\sin(kx)}{k} \right)'
= \sum_{k=1}^N \frac{ ( \sin(kx) )'}{k} 
= \sum_{k=1}^N \frac{ k \cdot \cos(kx) }{k}
= \sum_{k=1}^N \cos(kx)

　めでたく分母の $k$ を消すことが出来ました。この形なら総和計算の（$\sum$）を外せるような気がしてきました（とは言っても微分してしまったので後で積分して戻してあげる必要はありますが・・・）。オイラーの公式を用いて複素関数を経由して導出することも可能ですが、ここでは複素関数を使用しないで導出することにします。まず準備として等比数列 $ \{ ar^{k-1} \}$ の総和の公式を思い出してみましょう。次のような感じだったと思います。

\begin{eqnarray}
S_N &=&  a( r^0 + r^1 + \cdots + r^{N-1}) \\
r \cdot S_N &=& a( r^1 + r^2 + \cdots + r^N) \\
(1 - r)S_N &=& a(1 - r^N) \\
\therefore S_N &=& \frac{a(1 - r^N) }{1 - r} 
\end{eqnarray}

　これと同じような要領で総和計算の（$\sum$）を外してみましょう。まず $D_N(x) = \sum_{k=1}^N \cos(kx)$ と置いて両辺に$\cos(x)$を掛けます。

\begin{eqnarray}
\cos(x) D_N(x) &=& \cos(x) \sum_{k=1}^N \cos(kx) \\
&=& \sum_{k=1}^N \{ \cos(kx) \cos(x) \}　\\
&=& \frac{1}{2} \sum_{k=1}^N \{ \cos((k-1)x) + \cos((k+1)x) \} \\
&=& \frac{1}{2} \{ 1 + \cos(x) + \cdots + \cos((N-1)x) \\
&& \quad \quad \quad \quad + \cos(2x) + \cos(3x) + \cdots + \cos((N+1)x) \}
\end{eqnarray}

　この式に$-D_N(x) = -\cos(x) -\cos(2x) - \cdots - \cos(Nx)$を足せば、総和の計算が消せます。

(\cos(x)-1) D_N(x) = \frac{1}{2} \{1 - \cos(x) - \cos(Nx) + \cos((N+1)x) \}

　$D_N(x)$ についてもう少しまとめてみましょう。

\begin{eqnarray}
D_N(x) &=& \frac{1}{2} \cdot \frac{ \{ \cos(Nx) - \cos((N+1)x) \}  - \{ 1 - \cos(x) \} }{1 - \cos(x)} \\
&=& \frac{1}{2} \cdot \frac{ \sin(x/2)\sin((N+1/2)x) -\sin^2(x/2) }{ \sin^2(x/2)} \\
&=& \frac{1}{2} \left( \frac{\sin((N+1/2)x)}{\sin(x/2)} - 1 \right) 
\end{eqnarray}

　よって $g'_N(x)$ は次のようになります。

g'_N(x) = (2 / \pi) \cdot D_N(x) = 
\frac{1}{\pi} \left( \frac{\sin((N+1/2)x)}{\sin(x/2)} - 1 \right)

積分近似

　これでめでたく（$\sum$）を外すことが出来ました。次に $g_N(x)$微分してしまったので元に戻してあげる必要があります。 微分積分学の基本定理 を用いると次の式が得られます。

g_N(x) = \int_0^x g_N'(t) dt + g_N(0) 

　簡単に言うと「微分した関数を積分すると元に戻るよ（※）」ですが、墓穴を掘りそうなので説明はこのくらいにさせてください。$g'_N(x)$に先程の結果を代入してみましょう。

g_N(x) = \frac{1}{\pi} \int_0^x \left( \frac{\sin((N+1/2)t)}{\sin(t/2)} - 1 \right) dt

　総和 ($\sum$) が無くなった代わりに積分($\int$)が登場するようになりました。積分の計算はどうすれば良いでしょうか。解析的に求めようとすると最初の式（加算合成の式）に戻ってしまうのでここは近似で求めるしかなさそうです。その前にノコギリ波の周波数$f$を導入しましょう。

g_{N,f}(x) = g_N(2\pi f x)
= \frac{1}{\pi} \int_0^{2\pi f x} \left( \frac{\sin((N+1/2)t)}{\sin(t/2)} - 1 \right) dt

　サンプリング周波数を$f_s$と置いて離散化します。サンプリング点$\{t_m\}$を次のように置きます。

t_m = m \Delta t \quad (\Delta t = \frac{2\pi f}{f_s} )

　サンプリング点$\{t_m\}$を用いて$g_{N,f}(t_m)$を 長方形近似 すると次の式が得られます。

g_{N,f}(t_m) \approx \frac{1}{\pi} \sum_{k=0}^{m-1} \left( \frac{\sin((N+1/2) t_k)}{\sin(t_k/2)} - 1 \right)
\Delta t

　積分の精度を上げる（加算合成の結果に近づける）という点では台形公式やシンプソン公式を使用するのもありですが、頑張らないことにします。漸化式で表現すると次のようになります。

\begin{eqnarray}
&&g_{N,f}(t_0) = 0 \\
&&g_{N,f}(t_m) \approx g_{N,f}(t_{m-1}) + 
\frac{1}{\pi} \left( \frac{\sin((N+1/2) t_{m-1})}{\sin(t_{m-1}/2)} - 1 \right) \Delta t
\quad \quad (m \geq 1)
\end{eqnarray}

BLIT合成の実装

とりあえず実装

　やっと目標の式が得られました。では実装してノコギリ波の波形をグラフにして表示してみましょう。Gnuplot表示用のdatファイルを作成します。

blit_test_1.py

# -*- coding: utf-8 -*-
import math

f = 440.0    # 波形の周波数
fs = 44100.0 # サンプリング周波数

dt = 2*math.pi*f/fs # 刻み間隔
N = int((fs/2)/f)   # 倍音数(切り捨て)

t = 0.0          # 位置[0, 2pi)
integrator = 0.0 # 積分器
for i in range(int(3.5*fs/f)):
    # output
    print integrator

    # update integrator
    integrator += 1/math.pi*(math.sin((N+0.5)*t)/math.sin(0.5*t)-1)*dt

    # update position
    t += dt
    if t >= 2*math.pi:
        t -= 2*math.pi

　実際にVSTプラグインなどのリアルタイム処理では負荷を軽くするためにsin関数を使わずにウェーブテーブルを使用するなど工夫しますが、ここでは頑張らないことにします。では実行してみましょう。

実行結果

Traceback (most recent call last):
  File "blit_test_1.py", line 17, in <module>
    integrator += 1/math.pi*(math.sin((N+0.5)*t)/math.sin(0.5*t)-1)*dt
ZeroDivisionError: float division by zero

　あびゃ～。 ゼロ割 の考慮がおもいっきり抜けていました。

ゼロ割回避

　ゼロ割は math.sin((N+0.5)*math.pi*t)/math.sin(0.5*t) が $t=0$ のときに 不定形 $(0/0)$になってしまうのが原因です。ロピタルの定理を使うか、分母と分子それぞれをテイラー展開するなどで極限値を求めることも可能ですが、$g_N'(x) = (2 / \pi) \cdot \sum_{k=1}^N \cos(kx)$ から $g_N'(0)$ の値を計算してみましょう。

g'_{N,f}(0) = g'_N(0) = (2 / \pi) \cdot \sum_{k=1}^N \cos(0)
= (2 / \pi) \cdot \sum_{k=1}^N 1 = \frac{2N}{\pi} 

　あっさり求まりました。では $t$ が $0$ または $2\pi$ に限りなく近い場合の特化処理を追加してみます。

blit_test_2.py

# -*- coding: utf-8 -*-
# ゼロ割回避
import math

f = 440.0    # 波形の周波数
fs = 44100.0 # サンプリング周波数

dt = 2*math.pi*f/fs # 刻み間隔
N = int((fs/2)/f)   # 倍音数(切り捨て)

t = 0.0          # 位置[0, 2pi)
integrator = 0.0 # 積分器
for i in range(int(3.5*fs/f)):
    # output
    print integrator

    # update integrator
    if 1e-10 < t and t < 2*math.pi-1e-10:
        blit = 1/math.pi*(math.sin((N+0.5)*t)/math.sin(0.5*t)-1)
    else:
        blit = 1/math.pi*(2*N) # ゼロ割回避
    integrator += blit*dt

    # update position
    t += dt
    if t >= 2*math.pi:
        t -= 2*math.pi

　閾値の取り方は適当です。結果はどうでしょうか・・・。正常に終了しましたので結果をGnuplotに表示させてみましょう。

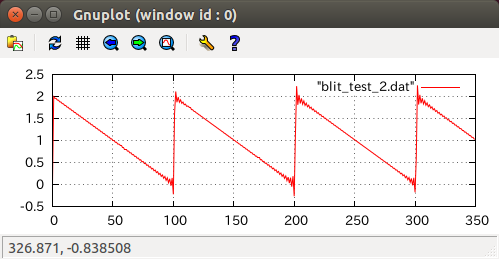
　残念！波形の形はいい感じなんですが・・・。-1～+1で振動するのを期待していましたが0～+2で振動しちゃってますね。

初期位相の調整

　初回の帯域制限インパルスでの持ち上げが大きすぎて+2まで達しちゃってます。恐らく積分計算が長方形近似で甘いのが原因だと思いますが、ここでは初回で帯域制限インパルスによる持ち上げが発生しないように初期位相を $t=\pi$ としてみます。

blit_test_3.py

# -*- coding: utf-8 -*-
# ゼロ割回避+初期位相の調整
import math

f = 440.0    # 波形の周波数
fs = 44100.0 # サンプリング周波数

dt = 2*math.pi*f/fs # 刻み間隔
N = int((fs/2)/f)   # 倍音数(切り捨て)

t = math.pi      # 位置[0, 2pi) 半分ずらした位置から始める
integrator = 0.0 # 積分器
for i in range(int(3.5*fs/f)):
    # output
    print integrator

    # update integrator
    if 1e-10 < t and t < 2*math.pi-1e-10:
        blit = 1/math.pi*(math.sin((N+0.5)*t)/math.sin(0.5*t)-1)
    else:
        blit = 1/math.pi*(2*N) # ゼロ割回避
    integrator += blit*dt

    # update position
    t += dt
    if t >= 2*math.pi:
        t -= 2*math.pi

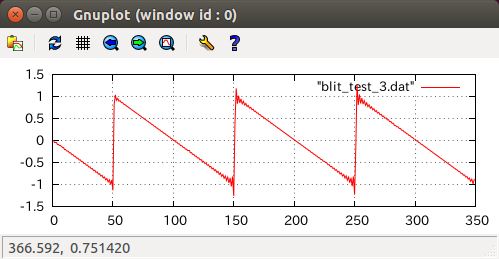
　結果はどうでしょうか・・・。再度Gnuplotに表示させてみましょう。

　やりました！目標の波形が出力出来た気がします。初回でゼロ割回避の処理は適用されなくなりますが、処理中に分母が0または限りなく0に近くなることは十分ありえるのでゼロ割回避は残しておきましょう。

leaky integrator

　実はまだ問題が残っています。それは発音中に周波数$f$を急激に変更すると DCオフセット が発生することがある（波形が上または下に寄ってしまう）という問題です。例えば、-1から+1に持ち上げる帯域制限インパルスを拾い損ねると+1まで持ち上がらずに波形が下に沈んでしまします。また、周波数を変更しない場合でも少なからず計算誤差は発生していますのでDCオフセットに関与していないわけではありません。この問題を回避する方法として leaky integrator という技があります。

leaky_integrator

integrator = 0.995*integrator + blit*dt

　0.995というのは適当ですが1未満の値を指定します。積分値を累積する際に一定の割合で捨てることによりDCオフセットを削っていくという作戦です。組み込んでみましょう。

blit_test_4.py

# -*- coding: utf-8 -*-
# ゼロ割回避+初期位相の調整+leaky integrator
import math

leak = 0.995 # leak値
f = 440.0    # 波形の周波数
fs = 44100.0 # サンプリング周波数

dt = 2*math.pi*f/fs # 刻み間隔
N = int((fs/2)/f)   # 倍音数(切り捨て)

t = math.pi      # 位置[0, 2pi) 半分ずらした位置から始める
integrator = 0.0 # 積分器
for i in range(int(3.5*fs/f)):
    # output
    print integrator

    # update integrator
    if 1e-10 < t and t < 2*math.pi-1e-10:
        blit = 1/math.pi*(math.sin((N+0.5)*t)/math.sin(0.5*t)-1)
    else:
        blit = 1/math.pi*(2*N) # ゼロ割回避
    integrator = leak*integrator + blit*dt # leaky integrator

    # update position
    t += dt
    if t >= 2*math.pi:
        t -= 2*math.pi

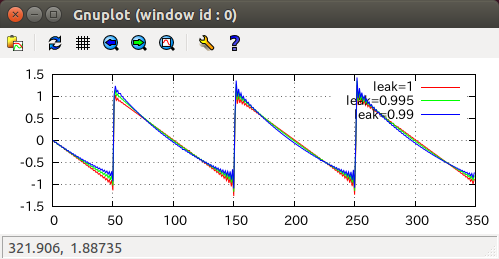
　leaky integratorなし版とあり版の波形を比較すると次のようになります。

　leak=1がleaky integratorなしに相当します。見にくいですが微妙に変形しちゃっているのが解ります。最後にDCオフセットが除去出来るかleaky integratorの効果を試してみましょう。

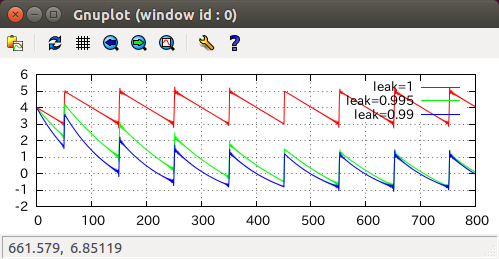
　初期値に誤差を仕込んで実行してみました。次第にDCオフセットが除去されていく様子が解ります。leak値を小さくするとDCオフセットの減衰が速くなりますが、DCオフセットでない部分の削りも大きくなるため波形が歪みが目立つようになります。その辺はトレードオフという感じでしょうか。