Pythonで最適化問題を解く。良いサンプルはないものかと思って探していたら、Nelder Mead法を実装しているMATLABの関数fminsearchが良さそう。
MATLABの例
MATLABには、最適化のための関数を揃えたoptimization toolboxという有料オプションがあるが、MATLAB本体だけがインストールしてある状態でもこのfminsearchを使うことはできる。
a = sqrt(2);
banana = @(x)100*(x(2)-x(1)^2)^2+(a-x(1))^2;
[x,fval] = fminsearch(banana, [-1.2, 1], optimset('TolX',1e-8));
これは、fminsearchのページに説明されている例そのままだけれど、この式を最小化するXをNelder-Mead法で求めている。
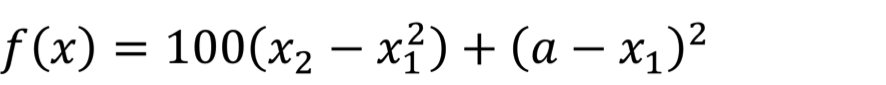
Pythonに移植
上記のbanana関数の例を、Pythonに移植する。Pythonでこの最適化問題を解くためには、Scipyの力を借りる。
Scipy.optimize
Scipy.optimizeにて、いろいろな最適化アルゴリズムが実装されていることが、ドキュメントを見ると分かる。
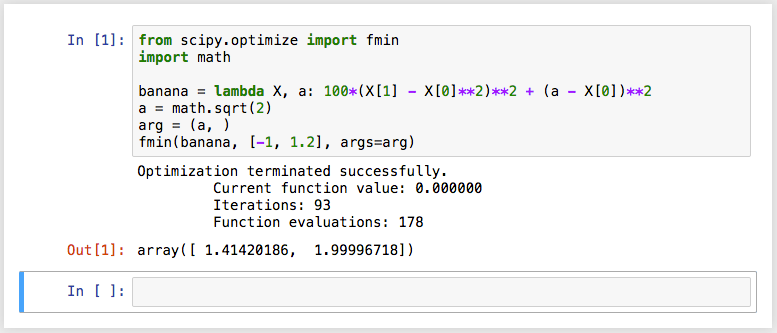
単純に移植すると、次のようになる。
from scipy.optimize import fmin
import math
banana = lambda X, a: 100*(X[1] - X[0]**2)**2 + (a - X[0])**2
a = math.sqrt(2)
arg = (a, )
fmin(banana, [-1, 1.2], args=arg)
(x1, x2) = (-1, 1.2)という初期値をおいて、上記の式の値を最小化するべく最適化を行ったところ、(x1, x2) = (1.41420186, 1.99996718) という結果が得られた、ということを示している。
ここでまず大事なのは、lambdaによる関数の定義だ。とはいえ、これはPythonのチュートリアルをやると必ず出てくる内容でもあるし、そんなに気にするポイントではないかもしれない。ここでは、「Xというリストと、aという変数を引数として渡す」ということが重要で、fminによって調整される変数はXというリストで渡される2つの変数であり、aは定数として渡されるということを意味している。もちろん、普通に以下のように定義してもよい。
def banana(X, a):
return 100*(X[1] - X[0]**2)**2 + (a - X[0])**2
さて、fminの引数は、最小化する目的関数と、その関数値を最小化するために最適化することを目的とする変数と、fminによる最適化をする対象ではないけれど関数に入力する引数のタプルである。
今回、目的関数bananaに入力する引数のうち定数として入力するaは、fminの引数argsにタプルとして渡すので、arg=(a, )としている。要素数が1のタプルを定義する場合は、「,」で終わる必要がある。
最適化のためのオプション設定
最適化のために、様々なオプションを設定することができる。最適化というヤツは「関数の値が収束するまでパラメーターをいじる」ということをするのだけれど、「収束した」と判断する条件は様々だ。その条件を設定することができる。詳細は、ドキュメントのとおり。
では、最大関数評価の回数を400回、反復の最大回数を400回、関数の終了値許容誤差を1e-4、Xの許容誤差を1e-4とする(MATLABのfminsearchのdefault値)と決めて、明示的にソレを指定するには、以下のようにfminを呼ぶ。
fmin(banana, [-1, 1.2], args=arg, xtol=1e-4, ftol=1e-4, maxiter=400, maxfun=400)
最適化過程を可視化したい
さて、banana関数程度の最適化だと、一瞬で終わってしまうのだけれど、この最適化計算の過程を可視化したい場合がある。
そういう場合には、callback関数を指定し、iterationごとの値を取り出すようにする。
count = 0
def cbf(Xi):
global count
count += 1
print('%d, %f, %f, %f' % (count, Xi[0], Xi[1], banana(Xi, math.sqrt(2))))
これが正しいやり方なのかどうかちょっと自信がないのだけれど、iterationの回数をグローバル変数として持って、カウントアップして表示するようにしてみた。
iterationごとに計算結果をテキストで出力するのではなくて、グラフに表現することもできる。
from scipy.optimize import fmin
import math
import matplotlib.pyplot as plt
count = 0
plt.axis([0, 100, 0, 6.5])
plt.ion()
def cbf(Xi):
global count
count += 1
f = banana(Xi, math.sqrt(2))
print('%d, %f, %f, %f' % (count, Xi[0], Xi[1], f))
plt.scatter(count, f)
banana = lambda X, a: 100*(X[1] - X[0]**2)**2 + (a - X[0])**2
a = math.sqrt(2)
arg = (a, )
fmin(banana, [-1, 1.2], args=arg, callback=cbf)
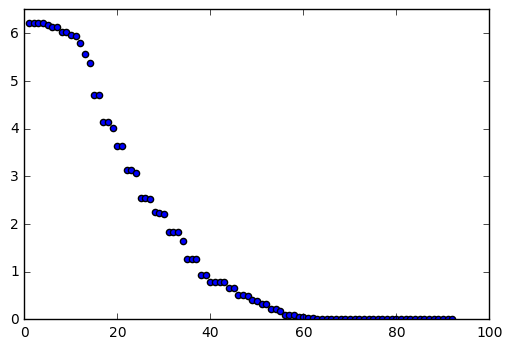
これで、matplotlibでグラフに点がリアルタイムにplotされていく様子を見ることができる。
最適化計算結果の取り出し
fminによる計算結果として、上述のように(x1, x2) = (1.41420186, 1.99996718) という結果が得られたとして、人は往々にしてその結果が得られた過程についてもう少し詳しく説明するように求めがちである。いや、ウチの上司もね(以下略)…。
そのためのfminのオプションとして、retallとfull_outputいう引数があり、これにTrueを設定すると、fminの戻り値を各種取得することができる。
[xopt, fopt, iter, funcalls, warnflag, allvecs] = fmin(banana, [-1, 1.2], args=arg, retall=True, full_output=True)
xoptは最適化されたパラメーターであり、foptがその時の最小化された関数の戻り値である。iterとfuncalllsはiterationが何回行われたのかで、warnflagは「収束した」と判断した条件が格納されている。allvecs には、各iterationで最適化の対象となっている変数の値(上述のbanana関数の例でいうとx1とx2の値)が格納されている。
ということで、iterationごとに変数が調整されていった履歴が必要な場合は、callback関数内で処理せずとも、fminによる最適化後にグラフ化するなど可視化することができる。
本日のまとめ
ということで、MATLABのfminsearch関数の例を引き合いにだして、Pythonで同様のことを実施してみた。
from scipy.optimize import fmin
import math
import matplotlib.pyplot as plt
def cbf(Xi):
global count
count += 1
f = banana(Xi, math.sqrt(2))
plt.scatter(count, f)
plt.pause(0.05)
def banana(X, a):
return 100*(X[1] - X[0]**2)**2 + (a - X[0])**2
def main():
a = math.sqrt(2)
arg = (a, )
[xopt, fopt, iter, funcalls, warnflag, allvecs] = fmin(
banana,
[-1, 1.2],
args=arg,
callback=cbf,
xtol=1e-4,
ftol=1e-4,
maxiter=400,
maxfun=400,
disp=True,
retall=True,
full_output=True)
for item in allvecs:
print('%f, %f' % (item[0], item[1]))
if __name__ == '__main__':
count = 1
plt.axis([0, 100, 0, 6.5])
main()