概要
構造最適化は、あらかじめ決められた設計・境界条件から、性能を最大限に発揮できる最適な構造や形状を求める方法です。その中で、トポロジー最適化があります。
土木分野でも研究されており、土木設計などに適応できると考えております。例えば、コンクリートを生成する際に大量の二酸化炭素を放出します。最適なコンクリート構造物を設計することで(不要なコンクリート部分を削減することで)、コンクリートの生成量を抑えることができ、二酸化炭素を減らすことができます。
他には、コンクリートは圧縮力に強いが引張力に弱いことが知られており、引張応力が生じる箇所には steel を挿入して引張応力に耐えられるように設計します。トポロジー最適化を用いることで steel を挿入する最適な箇所(引張応力が生じる箇所)を知ることができます。
前回の記事では、コンクリート構造物におけるトポロジー最適化を紹介しました。
今回の記事では、コンクリート構造物に Steel を考慮したトポロジー最適化について紹介します。
参考文献
以下の書籍を参考にしています。
FEMの基礎方程式
FEMの基礎方程式は、
\begin{align}
{\bf K}(\chi,\varphi){\bf U} ={\bf F}
\end{align}
と書くことができる。${\bf K}$は剛性行列であり、 ${\bf U}$ は変位ベクトル、${\bf F}$ は荷重ベクトルである。$\chi,\varphi$ は後に説明する設計変数である。
Bi-material 構造
要素 $e$ におけるコンクリートの要素剛性行列を ${\bf k}_e^c$ 、Steel の要素剛性行列を ${\bf k}_e^s$ とすると要素剛性行列 ${\bf k}_e$ は、
\begin{align}
{\bf k}_e(\chi_e,\varphi_e) = \chi_e^p \left(\varphi_e {\bf k}_e^c + (1-\varphi_e) {\bf k}_e^s \right)
\end{align}
と表現できる。$\chi$ はコンクリートの体積制約に関する設計変数であり、$\varphi$ は Steel の有無に関する設計変数である。$\varphi_e = 0$ のとき要素 $e$ は Steel に対応し、$\varphi_e = 1$ のとき要素 $e$ はコンクリートに対応する。
最適化問題は、体積制約を課した平均コンプライアンス最小化によって定式化され、目的関数を
\begin{align}
f(\chi,\varphi)=c= {\bf U}^T {\bf K}(\chi,\varphi) {\bf U}
= \sum_{e=1}^{N_e} {\bf u}_e^T {\bf k}_e(\chi_e,\varphi_e) {\bf u}_e
\end{align}
と書くことができる。$u_e$ は要素 $e$ における変位であり、$N_e$ は要素数である。体積制約は、要素 $e$ における体積を$v_e$、体積減率を$\beta$ として
\begin{align}
g(\chi) = V(\chi) -\beta V^0 = \sum_{e=1}^{N_e} \chi_e v_e -\beta\sum_{e=1}^{N_e} v_e \leq 0
\end{align}
と書くことができる。設計変数の範囲は、
\begin{align}
0< \chi_e^L \leq &\chi_e \leq \chi_e^U=1 \\
0 \leq &\varphi_e \leq 1
\end{align}
である。(下限値を$x_e^L=10^{-3}$に設定する)
ラグランジュ関数と停留条件
上記の最適化問題をラグランジュ関数で表すと
\begin{align}
L &= f(\chi,\varphi) + \Lambda g(\chi) \\
& + \sum_{e=1}^{N_e}\lambda_e (x_e^L-x_e)
+ \sum_{e=1}^{N_e}\gamma_e (x_e-x_e^U)
+ \sum_{e=1}^{N_e}\delta_e (0-\varphi_e)
+ \sum_{e=1}^{N_e}\zeta_e (\varphi_e-1)
\\
&= {\bf U}^T {\bf K}(\chi,\varphi){\bf U} + \Lambda\left( \sum_{e=1}^{N_e} (x_e-\beta) v_e \right) \\
& + \sum_{e=1}^{N_e}\lambda_e (x_e^L-x_e)
+ \sum_{e=1}^{N_e}\gamma_e (x_e-x_e^U)
+ \sum_{e=1}^{N_e}\delta_e (0-\varphi_e)
+ \sum_{e=1}^{N_e}\zeta_e (\varphi_e-1)
\\
& \Lambda \geq 0 \ , \ \lambda_e \geq 0 \ , \ \gamma_e \geq 0
, \ \delta_e \geq 0 \ , \ \zeta_e \geq 0
\end{align}
となる。$\Lambda, \lambda_e ,\gamma_e,\delta_e ,\zeta_e$ はラグランジュ未定乗数である。
ラグランジュ関数を設計変数で微分し停留条件を求めると、
\begin{align}
\frac{\partial L}{\partial \chi_e} &= \frac{\partial {\bf U}^T}{\partial \chi_e} {\bf K} {\bf U} + {\bf U}^T \frac{\partial {\bf K}}{\partial \chi_e} {\bf U} +
{\bf U}^T {\bf K} \frac{\partial {\bf U}}{\partial \chi_e} +
\Lambda v_e -\lambda_e + \gamma_e = 0 \\
\frac{\partial L}{\partial \varphi_e} &= \frac{\partial {\bf U}^T}{\partial \varphi_e} {\bf K} {\bf U} + {\bf U}^T \frac{\partial {\bf K}}{\partial \varphi_e} {\bf U} +
{\bf U}^T {\bf K} \frac{\partial {\bf U}}{\partial \varphi_e} +
\Lambda v_e -\delta_e + \zeta_e = 0 \\
\end{align}
であるが、荷重は設計変数に依らないこと、つまり、
\begin{align}
&\frac{\partial }{\partial \chi_e}\left({\bf K}{\bf U}-{\bf F} \right)=0 \Longrightarrow \ \ \therefore {\bf K}\frac{\partial {\bf U}}{\partial \chi_e} = -\frac{\partial {\bf K} }{\partial \chi_e}{\bf U} \\
&\frac{\partial }{\partial \varphi_e}\left({\bf K}{\bf U}-{\bf F} \right)=0 \Longrightarrow \ \ \therefore {\bf K}\frac{\partial {\bf U}}{\partial \varphi_e} = -\frac{\partial {\bf K} }{\partial \varphi_e}{\bf U} \\
\end{align}
であることと、剛性行列は対称行列とすれば停留条件は、
\begin{align}
\frac{\partial L}{\partial \chi_e} &= -{\bf U}^T \frac{\partial {\bf K}}{\partial \chi_e} {\bf U} +\Lambda v_e -\lambda_e + \gamma_e = 0 \\
\frac{\partial L}{\partial \varphi_e} &= - {\bf U}^T \frac{\partial {\bf K}}{\partial \varphi_e} {\bf U} +
\Lambda v_e -\delta_e + \zeta_e = 0 \\
\end{align}
となる。
Sensitivity 解析
目的関数を設計変数で微分すると、
\begin{align}
\frac{\partial f(\chi_e,\varphi_e)}{\partial \chi_e} &= -{\bf U}^T \frac{\partial {\bf K}}{\partial \chi_e} {\bf U} = -p\chi_e^{p-1} {\bf u}^T_e \left(\varphi_e {\bf k}_e^c + (1-\varphi_e) {\bf k}_e^s \right) {\bf u}_e \\
\frac{\partial f(\chi_e,\varphi_e)}{\partial \varphi_e} &= -{\bf U}^T \frac{\partial {\bf K}}{\partial \varphi_e} {\bf U} = -\chi_e^{p} {\bf u}^T_e \left({\bf k}_e^c-{\bf k}_e^s \right) {\bf u}_e \\
\end{align}
と書くことができる。目的関数の設計変数微分を設計感度という。
コンクリートは圧縮応力には強いが引張応力に弱いため、応力状態によって設計感度を修正したい。コンクリートと Steel の修正因子を $R_e^c,R_e^s$ として、
\begin{align}
\frac{\partial f(\chi_e,\varphi_e)}{\partial \chi_e} &=
-p\chi_e^{p-1} {\bf u}^T_e \left(\varphi_e R_e^c{\bf k}_e^c + (1-\varphi_e) R_e^s{\bf k}_e^s \right) {\bf u}_e \\
\frac{\partial f(\chi_e,\varphi_e)}{\partial \varphi_e} &=
-\chi_e^{p} {\bf u}^T_e \left(R_e^c{\bf k}_e^c-R_e^s{\bf k}_e^s \right) {\bf u}_e \\
\end{align}
設計感度を上式のように応力状態に依存するように修正する。
修正因子は、まず各要素においてひずみと応力を求め、圧縮部分と引張部分に分離する。
\begin{align}
{\bf \varepsilon}_e &= {\bf \varepsilon}_e^{-} + {\bf \varepsilon}_e^{+} \\
{\bf \sigma}_e &= {\bf \sigma}_e^{-} + {\bf \sigma}_e^{+} \\
\end{align}
上付き添え字 $-$ は圧縮を意味し、$+$ は引張を意味する。コンクリートとSteel の修正因子は、
\begin{align}
R_e^c = \frac{{\bf \sigma}_e^{-}{\bf \varepsilon}_e^{-} }{{\bf \sigma}_e{\bf \varepsilon}_e }
\ \ , \ \
R_e^s = \frac{{\bf \sigma}_e^{+}{\bf \varepsilon}_e^{+} }{{\bf \sigma}_e{\bf \varepsilon}_e }
\end{align}
として、
\begin{align}
R_e^c+R_e^s = 1
\end{align}
を満たすように計算する。
ここで、修正因子の閾値を導出するために
\begin{align}
\frac{\partial f(\chi_e,\varphi_e)}{\partial \varphi_e} \to 0
\end{align}
の極限を考える。このときのコンクリートの修正因子は$R_e^c \to R_e^{\ast}$ となり、$R_e^s = 1-R_e^c$ の関係式を用いると
\begin{align}
&{\bf u}^T_e \left(R_e^{\ast}{\bf k}_e^c-(1-R_e^{\ast}){\bf k}_e^s \right) {\bf u}_e = 0 \\
\Longrightarrow
& \ \ R_e^{\ast} = \frac{{\bf u}^T_e {\bf k}_e^s {\bf u}_e}{{\bf u}^T_e \left({\bf k}_e^c+{\bf k}_e^s \right) {\bf u}_e}
\end{align}
となる。この式から以下が言える。
- $R_e^{\ast}\leq R_e^{c}$ ならばコンクリート(圧縮応力)が支配的になり設計変数 $\varphi_e$ は 増加方向になる。
- $R_e^{\ast}>R_e^{c}$ ならばSteel(引張応力)が支配的になり設計変数 $\varphi_e$ は 減少方向になる。
Bi-material フィルタリング
トポロジー最適化は、チェッカーボードの問題が生じるためフィルタリングを行うが、コンクリートとSteelでは制約が異なるため、フィルタリングのパラメータ$r_{\min}$も異なる。コンクリートと Steel のフィルタリングのパラメータを$r_{\min}^c,r_{\min}^s$とすると、設計感度は
\begin{align}
\frac{\partial \tilde{f}(\chi_e,\varphi_e)}{\partial \chi_e} &= \frac{\varphi_e}{\chi_e\sum_{i=1}^{N_e}H_{ei}\left(r_{\min}^c\right)} \sum_{i=1}^{N_e}H_{ei}\left(r_{\min}^c\right) \chi_i\frac{\partial f(\chi_i,\varphi_i)}{\partial \chi_i} \\
& + \frac{1-\varphi_e}{\chi_e\sum_{i=1}^{N_e}H_{ei}\left(r_{\min}^s\right)} \sum_{i=1}^{N_e}H_{ei}\left(r_{\min}^s\right) \chi_i\frac{\partial f(\chi_i,\varphi_i)}{\partial \chi_i}
\\
\frac{\partial \tilde{f}(\chi_e,\varphi_e)}{\partial \varphi_e} &= \frac{1}{\sum_{i=1}^{N_e}H_{ei}\left(r_{\min}^s\right)} \sum_{i=1}^{N_e}H_{ei}\left(r_{\min}^s\right) \frac{\partial f(\chi_i,\varphi_i)}{\partial \varphi_i} \\
H_{ei}(r_{\min}) &= \begin{cases}
r_{\min} -\Delta_{ei} & \Delta_{ei} \leq r_{\min} \\
0 & r_{\min} < \Delta_{ei}
\end{cases}
\end{align}
と書くことができる。$\Delta_{ei}$ は要素 $e$ と $i$ の中心からの距離である。
設計変数の更新
最適基準法を用いて設計変数を更新する。フィルタリングされた設計感度はコンクリートとSteel の圧縮応力と引張応力を考慮する必要がある。$\chi_e$ については、
\begin{align}
X_e \equiv -\frac{\frac{\partial \tilde{f}(\chi_e,\varphi_e)}{\partial \chi_e}}{ \Lambda v_e }=1
\end{align}
となるように $\Lambda$ を決め $\chi_e$ を更新する。$\chi_e$ の更新は、$k$ を繰り返しステップ数とすると
\begin{align}
\chi_e^{(k+1)} =
\begin{cases}
M_{\chi}^{-} & \left[X_e^{(k)} \right]^{0.5} \chi_e^{(k)} \leq M_{\chi}^{-} \\
\left[X_e^{(k)} \right]^{0.5}\chi_e^{(k)} &
M_{\chi}^{-} < \left[X_e^{(k)} \right]^{0.5} \chi_e^{(k)} < M_{\chi}^{+} \\
M_{\chi}^{+} & M_{\chi}^{+}\leq \left[X_e^{(k)} \right]^{0.5} \chi_e^{(k)} \\
\end{cases}
\end{align}
\begin{align}
M_{\chi}^{-} &= \max \{(1-\mu)\chi_e^{(k)},\chi_e^L \} \\
M_{\chi}^{+} &= \max \{\chi_e^U,(1+\mu)\chi_e^{(k)} \} \\
\end{align}
となるように更新する。$\mu$ は move limit と呼ばれ $\mu =0.2$ に設定する。
$\varphi_e$ については、
\begin{align}
\Phi_e \equiv -\frac{\partial \tilde{f}(\chi_e,\varphi_e)}{\partial \varphi_e}=0
\end{align}
となるように$\varphi_e$を更新する。これらは応力状態に依存するように設定しなければならない。
$R_e^{\ast} \leq R_e^c$ ならば、設計変数 $\varphi_e$ を大きくするために
\begin{align}
\varphi_e^{(k+1)} =
\begin{cases}
M_{\varphi}^{-} & \left[\alpha\Phi_e^{(k)}+1 \right] \varphi_e^{(k)} \leq M_{\varphi}^{-} \\
\left[\alpha\Phi_e^{(k)}+1 \right]\varphi_e^{(k)} &
M_{\varphi}^{-}<\left[\alpha\Phi_e^{(k)}+1 \right]\varphi_e^{(k)} < M_{\varphi}^{+} \\
M_{\varphi}^{+} & M_{\varphi}^{+}\leq \left[\alpha\Phi_e^{(k)}+1 \right]\varphi_e^{(k)} \\
\end{cases}
\end{align}
$R_e^{\ast} > R_e^c$ ならば、設計変数 $\varphi_e$ を小さくするために
\begin{align}
\varphi_e^{(k+1)} =
\begin{cases}
M_{\varphi}^{-} & \left|\alpha\Phi_e^{(k)}-1\right|^{-1} \varphi_e^{(k)} \leq M_{\varphi}^{-} \\
\left|\alpha\Phi_e^{(k)}-1\right|^{-1}\varphi_e^{(k)} &
M_{\varphi}^{-}<\left|\alpha\Phi_e^{(k)}-1\right|^{-1}\varphi_e^{(k)} < M_{\varphi}^{+} \\
M_{\varphi}^{+} & M_{\varphi}^{+}\leq \left|\alpha\Phi_e^{(k)}-1\right|^{-1}\varphi_e^{(k)} \\
\end{cases}
\end{align}
と更新する。設計変数 $\varphi_e$ の下限値と上限値は、
\begin{align}
M_{\varphi}^{-} &= \max \{(1-\mu)\varphi_e^{(k)},\varphi_e^L \} \\
M_{\varphi}^{+} &= \max \{\varphi_e^U,(1+\mu)\varphi_e^{(k)} \} \\
\end{align}
であり、上記の方法で設計変数 $\varphi_e$ を更新すると
\begin{align}
0 \leq \alpha\Phi_e^{(k)} \leq 1
\end{align}
の不等式が保たれる。$\alpha$ は加速因子であり、$\alpha=100$ と設定する。元々、$R_e^{\ast} $ は、
\begin{align}
\frac{\partial f(\chi_e,\varphi_e)}{\partial \varphi_e} = 0
\end{align}
の条件より得られた条件なので、$R_e^{\ast}\leq R_e^{c}$ ならば $\Phi_e^{(k)} \geq 0$ 、$R_e^{\ast} > R_e^{c}$ ならば $\Phi_e^{(k)} < 0$ に対応するが、フィルタリングをしているため成立するとは限らない。
収束条件としては、
\begin{align}
\max \left| x_e^{(k+1)} - x_e^{(k)} \right| \leq 10^{-2}
\end{align}
を課し、設計変数が更新しなくなったら計算を終了する。
その他
修正因子を計算する際には、ひずみ・応力を圧縮成分と引張成分に分ける必要がある。そのために、平面応力を仮定し z 軸周りに $\theta$ 回転させることを考える。回転行列を
\begin{align}
{\bf R} =
\begin{pmatrix}
\cos \theta & \sin \theta & 0\\
-\sin \theta & \cos \theta & 0\\
0 & 0 & 1
\end{pmatrix}
\end{align}
とする。平面応力の場合、$\sigma_{xz} =\sigma_{yz} =\sigma_{zz} =0$ なので 3行目と3列目は不要である。変換された応力をプライム $\prime$ をつけて表現すると
\begin{align}
\begin{pmatrix}
\sigma_{xx}^{\prime} & \sigma_{xy}^{\prime} \\
\sigma_{xy}^{\prime} & \sigma_{yy}^{\prime} \\
\end{pmatrix}
=
\begin{pmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta \\
\end{pmatrix}
\begin{pmatrix}
\sigma_{xx} & \sigma_{xy} \\
\sigma_{xy} & \sigma_{yy} \\
\end{pmatrix}
\begin{pmatrix}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta \\
\end{pmatrix}
\end{align}
\begin{align}
\sigma_{xx}^{\prime} &= \sigma_{xx}\cos^2 \theta + \sigma_{yy}\sin^2 \theta - \sigma_{xy}\sin 2\theta \\
\sigma_{yy}^{\prime} &= \sigma_{xx}\sin^2 \theta + \sigma_{yy}\cos^2 \theta + \sigma_{xy}\sin 2\theta \\
\sigma_{xy}^{\prime} &= \frac{1}{2}\left(\sigma_{xx}- \sigma_{yy}\right) \sin 2\theta + \sigma_{xy} \cos 2\theta
\end{align}
となる。応力の成分を圧縮成分と引張成分に分けるため、変換されたせん断応力がゼロとなる $\theta$ を求める。すると、
\begin{align}
\sigma_{1} &= \sigma_{xx}\cos^2 \theta + \sigma_{yy}\sin^2 \theta - \sigma_{xy}\sin 2\theta \\
\sigma_{2} &= \sigma_{xx}\sin^2 \theta + \sigma_{yy}\cos^2 \theta + \sigma_{xy}\sin 2\theta \\
\theta &= \frac{1}{2} \tan^{-1} \frac{-2\sigma_{xy}}{\sigma_{xx}- \sigma_{yy}}
\end{align}
となる。$\sigma_{1}$ と $\sigma_{2}$ の符号から圧縮・引張成分を判断できる。修正因子は
\begin{align}
R_e^c+R_e^s = 1
\end{align}
を満たす必要があるため、ひずみも同様に、変換されたせん断応力がゼロとなる$\theta$ で回転させる。すると
\begin{align}
\varepsilon_{1} &= \varepsilon_{xx}\cos^2 \theta + \varepsilon_{yy}\sin^2 \theta - \varepsilon_{xy}\sin 2\theta \\
\varepsilon_{2} &= \varepsilon_{xx}\sin^2 \theta + \varepsilon_{yy}\cos^2 \theta + \varepsilon_{xy}\sin 2\theta \\
\end{align}
となる。従って、修正因子は以下のように設定する。
1.$\sigma_1 < 0 $ のとき
\begin{align}
R_e^c = 1 \ \ , \ \ R_e^s =0
\end{align}
2.$\sigma_1 > 0 $ かつ $\sigma_2 < 0 $のとき
\begin{align}
R_e^c = \frac{\sigma_2 \varepsilon_2 }{\sigma_1 \varepsilon_1+\sigma_2 \varepsilon_2 }
\ \ , \ \
R_e^s = \frac{\sigma_1 \varepsilon_1 }{\sigma_1 \varepsilon_1+\sigma_2 \varepsilon_2}
\end{align}
3.$\sigma_2 > 0 $のとき
\begin{align}
R_e^c = 0 \ \ , \ \ R_e^s =1
\end{align}
計算結果
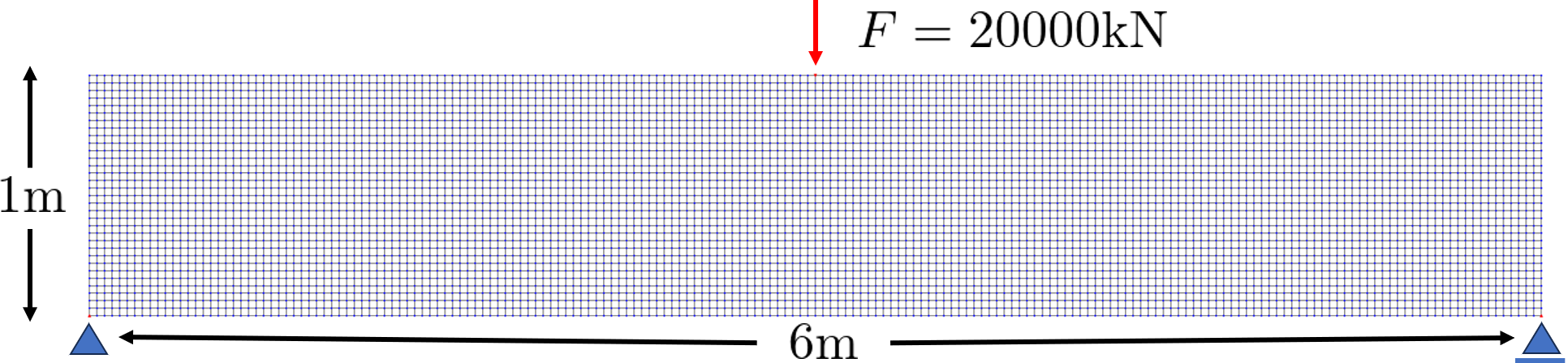
以下の図のように、幅 $6$m 、高さ $1$m のコンクリートに上端中央部から集中荷重 $20000 \mbox{kN}$ の荷重をかける。
コンクリートのヤング率とポアソン比は $50\mbox{Gpa} \ \ ,0.2$ とし、Steel のヤング率とポアソン比は $200\mbox{Gpa} \ \ ,0.3$ とし平面応力とした。体積の減率は $\beta = 0.3$ とした。フィルタリングで用いるパラメータ $r^c_{\min},r^s_{\min}$ は、最大となる要素辺の長さの $3.5$ 倍とした。
コンクリートの中央上部は圧縮力がかかり、中央下部は引張力がかかるので、中央下部に Steel が挿入されることが想定できる。
以下がトポロジー最適化の結果である。 $\chi$ の結果(コンクリート領域)であり、
$1-\varphi_e$ の結果(Steel 領域)である。
コンクリートの中央上部は圧縮力がかかるのでSteel は挿入されず、中央下部は引張力がかかるので、中央下部に Steel が挿入されることが確認できる。
まとめ
今回の記事では、トポロジー最適化を用いてコンクリート構造物に Steel を考慮した最適設計を行った。引張応力がかかるところには、Steel を挿入するような最適設計を行うことができた。