最急降下法および準ニュートン法に関するメモ

概要

　最適化問題を解く場合、最急降下法や準ニュートン法などが使われます。例えば、4次元変分法（データ同化）において、準ニュートン法が使われることが多いです。

最急降下法や準ニュートン法について、メモ程度に書き込んでいきます。

最適化問題

　目的関数 $f({\bf x})$ が最小となる ${\bf x}$ を求めることを考える。
　
以下の説明において、ランダウの o-記法を用いる。これは、

\begin{align}
\lim_{x\to 0} \left| \frac{g(x)}{x} \right| = 0
\end{align}

が成立するとき

\begin{align}
g(x) = o(x)
\end{align}

と表す。

最急降下法

最適性の１次の必要条件

　目的関数 $f({\bf x})$ は微分可能とする。このとき、点 ${\bf x}^{\ast}$ が局所最適解ならば、

\begin{align}
{\bf \nabla} f({\bf x}^{\ast}) =0
\end{align}

が成立。
（ただし、停留点においても$\nabla f({\bf x}^{\ast})=0$ が成立する。十分条件である「$\nabla f({\bf x}^{\ast})=0$ であるならば、点 ${\bf x}^{\ast}$ は局所最適解である。」は成立しない。）

証明

　局所最適解 ${\bf x}^{\ast}$ から、ある方向 ${\bf d}$ $(|{\bf d} |=1)$に沿って十分小さい $\alpha(>0)$ だけ動いた点を考える。$f({\bf x})$ は微分可能なので、

\begin{align}
f({\bf x}^{\ast}+\alpha\ {\bf d}) = f({\bf x}^{\ast}) + \alpha{\bf \nabla} f({\bf x}^{\ast})^T {\bf d}+o(\alpha)
\end{align}

と書ける。また、局所最適解 ${\bf x}^{\ast}$ においては、

\begin{align}
f({\bf x}^{\ast}+\alpha\ {\bf d}) \geq f({\bf x}^{\ast}) 
\end{align}

が成立するので、

\begin{align}
& f({\bf x}^{\ast}+\alpha\ {\bf d}) -f({\bf x}^{\ast})=\alpha\nabla f({\bf x}^{\ast})^T {\bf d}+o(\alpha) \geq 0 \\
\therefore \ \ &\nabla f({\bf x}^{\ast})^T {\bf d}+\frac{o(\alpha)}{\alpha} \geq 0 \\
& \downarrow \alpha \to 0 \\
&\nabla f({\bf x}^{\ast})^T {\bf d}\geq 0 \\
\end{align}

となる。任意の${\bf d}$ において成立するので、$\nabla f({\bf x}^{\ast})=0$ が成立。

最急降下法について

最適性の１次の必要条件より、$\nabla f({\bf x})=0$を解けば良い。$\nabla f({\bf x})=0$を解くために、反復法が用いられる。局所最適解 ${\bf x}^{\ast}$ に収束する点列
　

\begin{align}
\{{\bf x}_k \ \ |\ \ k=0,1,2,\ldots  \}
\end{align}

を生成し、局所最適解 ${\bf x}^{\ast}$ に十分近い ${\bf x}_k$ を近似解とする。

　点列は、${\bf x}_0$ から出発し

\begin{align}
{\bf x}_{k+1} = {\bf x}_k+\alpha_k {\bf d}({\bf x}_k)
\end{align}

を繰り返しながら生成していく。$\alpha(>0)$ はステップ幅、${\bf d}({\bf x}_k)$ は探索方向と言う。

　反復法の各ステップにおいて、新たに生成された ${\bf x}_{k+1}$ が、これまで生成された点列より小さくなるよう、つまり、　

\begin{align}
f({\bf x}_{k+1}) =f({\bf x}_k+\alpha_k {\bf d}({\bf x}_k)) < f({\bf x}_k) 
\end{align}

を満たすように、計算を行いたい。

　$f({\bf x})$ は、微分可能であるので

\begin{align}
f({\bf x}_k+\alpha_k {\bf d}({\bf x}_k)) \approx f({\bf x}_k) + \alpha_k \nabla f({\bf x}_k)^T {\bf d}({\bf x}_k)
\end{align}

と書くことができる。

十分小さな$\alpha_k$ に対して、降下方向

\begin{align}
 \nabla f({\bf x}_k)^T {\bf d}({\bf x}_k) <0
\end{align}

が成立するならば、

\begin{align}
f({\bf x}_{k+1}) =f({\bf x}_k+\alpha_k {\bf d}({\bf x}_k)) < f({\bf x}_k) 
\end{align}

が成立。

　最急降下法は、探索方向を

\begin{align}
 {\bf d}({\bf x}_k) = - \nabla f({\bf x}_k)^T
\end{align}

と定める。そうすれば、

\begin{align}
 \nabla f({\bf x}_k)^T {\bf d}({\bf x}_k)= -\left\| \nabla f({\bf x}_k)  \right\|^2 <0
\end{align}

となり、降下方向になる。

まとめると最急降下法は、${\bf x}_0$ から出発し

\begin{align}
{\bf x}_{k+1} = {\bf x}_k+\alpha_k {\bf d}({\bf x}_k)　\ \ , \ \  {\bf d}({\bf x}_k) = - \nabla f({\bf x}_k)^T
\end{align}

と計算しながら、近似解を求める。

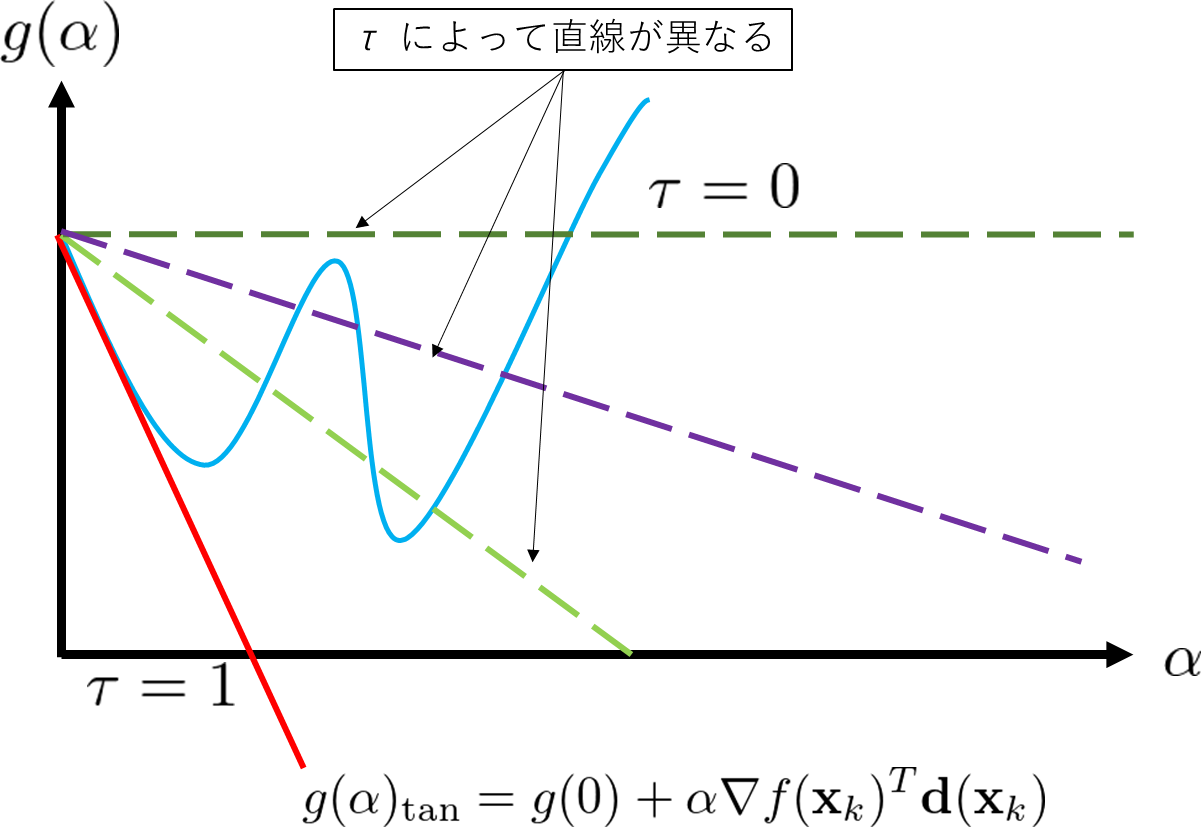
直線探索

　上記のように計算すれば、$f({\bf x})$ の値は減少するが、増加に転じる場合がある。この問題に関しては、ステップ幅 $\alpha$ を上手に定めることで対処する。これは、

\begin{align}
g(\alpha) =f({\bf x}_k+\alpha {\bf d}({\bf x}_k))
\end{align}

を最小化する$\alpha$ を求め、この$\alpha$ を $\alpha_k$として最適化問題の計算を進める。直接、この式を求めるのは難しいので、 以下の条件を満たすように、$\alpha_k$を定める。

　$f({\bf x})$ は微分可能であるので

\begin{align}
\frac{\mathrm{d} g(\alpha) }{\mathrm{d} \alpha} &=\frac{\mathrm{d}  }{\mathrm{d} \alpha} f({\bf x}_k+\alpha {\bf d}({\bf x}_k)) \\
&= {\bf \nabla}  f({\bf x}_k+\alpha {\bf d}({\bf x}_k))^T \frac{\mathrm{d}  }{\mathrm{d} \alpha} ({\bf x}_k+\alpha {\bf d}({\bf x}_k)) \\
&= {\bf \nabla}  f({\bf x}_k+\alpha {\bf d}({\bf x}_k))^T {\bf d}({\bf x}_k)
\end{align}

　$\alpha=0$ における接線の方程式は、

\begin{align}
g(\alpha)_{\tan} &= g(0) + \frac{\mathrm{d} g(0) }{\mathrm{d} \alpha}\alpha\\
&=g(0) +\alpha {\bf \nabla}  f({\bf x}_k)^T {\bf d}({\bf x}_k)
\end{align}

である。

　アルミホ条件は、$g(\alpha)$ が接線の方程式$g(\alpha)_{\tan}$ の傾きを $\tau$ 倍した直線より下部の領域に収まるように設定された条件である。

　アルミホ条件では、小さすぎる $\alpha$ が選ばれる可能性がある。傾きが$\alpha=0$ より緩やかになる条件

\begin{align}
\frac{\mathrm{d} g(\alpha) }{\mathrm{d} \alpha} \geq \frac{\mathrm{d} g(0)}{\mathrm{d} \alpha}
\end{align}

を入れた条件がウルフ条件である。
　降下法の計算より、$ \mathrm{d} g(0)/\mathrm{d} \alpha = {\bf \nabla} f({\bf x}_k)^T {\bf d}({\bf x}_k) <0$ である。$\alpha$を大きくすると勾配は、

\begin{align}
\frac{\mathrm{d} g(\alpha)}{\mathrm{d} \alpha}\geq 0
\end{align}

となるのでウルフ条件を満たし、小さすぎる $\alpha$ が選ばれる可能性を減らす。ただし、ウルフ条件は、$\mathrm{d} g(\alpha)/\mathrm{d}\alpha$ が簡単に計算できる場合に限る。

　まとめると、以下となる。

• アルミホ（Armijo）条件

\begin{align}
g(\alpha) \leq g(0) + \tau \alpha {\bf \nabla}  f({\bf x}_k)^T {\bf d}({\bf x}_k) \ \ , \ \ 0<\tau<1
\end{align}

• ウルフ（Wolfe）条件

\begin{align}
&g(\alpha) \leq g(0) + \tau_1 \alpha {\bf \nabla}  f({\bf x}_k)^T {\bf d}({\bf x}_k)  \\ 
&{\bf \nabla}  f({\bf x}_k+\alpha {\bf d}({\bf x}_k))^T {\bf d}({\bf x}_k) \geq \tau_2 {\bf \nabla}  f({\bf x}_k)^T {\bf d}({\bf x}_k)\\
&0 < \tau_1 < \tau_2 < 1
\end{align}

　以上の条件を満たすように、ステップ幅$\alpha$ を決めれば良いが、$\alpha$をどのように更新すればいいかわからない。

　$\alpha$の更新方法として、バックトラック法がある。バックトラック法は、$\alpha^{(0)}=1$ を初期値として、反復的に

\begin{align}
\alpha^{(i+1)} =\beta \alpha^{(i)}
\ \ , \ \ 0<\beta<1
\end{align}

として、更新していく。$i$ は直線探索におけるステップ数である。

　他に、セカント方があるが、$\mathrm{d} g(\alpha)/\mathrm{d}\alpha$ が簡単に計算できる場合に限る。
　

準ニュートン法

最適性の2次の必要条件

　目的関数 $f({\bf x})$ は２階微分可能とする。このとき、点 ${\bf x}^{\ast}$ が局所最適解ならば、ヘッセ行列は半正定値である。

\begin{align}
{\bf d}^T{\bf \nabla} ^2 f({\bf x}^{\ast}){\bf d} \geq 0
\end{align}

${\bf d}$ は任意のベクトルである。

証明

　局所最適解 ${\bf x}^{\ast}$ から、ある方向 ${\bf d}$ $(|{\bf d} |=1)$に沿って十分小さい $\alpha(>0)$ だけ動いた点を考える。$f({\bf x})$ は２階微分可能なので、

\begin{align}
f({\bf x}^{\ast}+\alpha\ {\bf d}) = f({\bf x}^{\ast}) + \alpha{\bf \nabla} f({\bf x}^{\ast})^T {\bf d}+ \frac{\alpha^2}{2}{\bf d}^T{\bf \nabla} ^2 f({\bf x}^{\ast}){\bf d}+o(\alpha^2)
\end{align}

と書ける。また、 局所最適解 ${\bf x}^{\ast}$ においては、

\begin{align}
f({\bf x}^{\ast}+\alpha\ {\bf d}) \geq f({\bf x}^{\ast}) 
\ \ , \ \ {\bf \nabla} f({\bf x}^{\ast}) =0 
\end{align}

が成立するので、

\begin{align}
& f({\bf x}^{\ast}+\alpha\ {\bf d}) -f({\bf x}^{\ast})=\frac{\alpha^2}{2}{\bf d}^T{\bf \nabla} ^2 f({\bf x}^{\ast}){\bf d}+o(\alpha^2) \geq 0 \\
\therefore \ \ &{\bf d}^T{\bf \nabla} ^2 f({\bf x}^{\ast}){\bf d}+\frac{o(\alpha^2)}{\alpha^2} \geq 0 \\
& \downarrow \alpha \to 0 \\
&{\bf d}^T{\bf \nabla} ^2 f({\bf x}^{\ast}){\bf d}\geq 0 \\
\end{align}

となり、${\bf d}$ は任意のベクトルなので、ヘッセ行列は半正定値である。

最適性の2次の十分条件

　目的関数 $f({\bf x})$ は２階微分可能とする。このとき、点 ${\bf x}^{\ast}$ が停留点で、ヘッセ行列が半正定値ならば、点 ${\bf x}^{\ast}$ は局所最適解である。

証明

　
　停留点 ${\bf x}^{\ast}$ から、ある方向 ${\bf d}$ $(|{\bf d} |=1)$に沿って十分小さい $\alpha(>0)$ だけ動いた点を考える。$f({\bf x})$ は２階微分可能なので、

\begin{align}
f({\bf x}^{\ast}+\alpha\ {\bf d}) = f({\bf x}^{\ast}) + \alpha{\bf \nabla} f({\bf x}^{\ast})^T {\bf d}+ \frac{\alpha^2}{2}{\bf d}^T{\bf \nabla} ^2 f({\bf x}^{\ast}){\bf d}+o(\alpha^2)
\end{align}

と書ける。停留点では ${\bf \nabla}f({\bf x}^{\ast})=0$ を満たし、ヘッセ行列は半正定値 ${\bf d}^T{\bf \nabla} ^2 f({\bf x}^{\ast}){\bf d}\geq0 $ を満たすので

\begin{align}
f({\bf x}^{\ast}+\alpha\ {\bf d})-f({\bf x}^{\ast}) &= \frac{\alpha^2}{2}{\bf d}^T{\bf \nabla} ^2 f({\bf x}^{\ast}){\bf d}+o(\alpha^2)\geq o(\alpha^2)
\\
& \downarrow \alpha \to 0 \\
f({\bf x}^{\ast}+\alpha\ {\bf d})-f({\bf x}^{\ast}) &\geq 0
\end{align}

が成立。任意の ${\bf d}$ において成立するので、停留点 ${\bf x}^{\ast}$ は局所最適解である。

準ニュートン法について

　準ニュートン法は、正定値対称行列 ${\bf B}_k$ を用いて、最急降下法における探索方向を

\begin{align}
 {\bf d}({\bf x}_k) = -{\bf B}_k^{-1} \nabla f({\bf x}_k)
\end{align}

と定める。すると、正定値対称行列の特性から

\begin{align}
 \nabla f({\bf x}_k)^T {\bf d}({\bf x}_k)= - \nabla f({\bf x}_k)^T{\bf B}_k^{-1}\nabla f({\bf x}_k)  <0
\end{align}

となり、降下方向になる。正定値対称行列 ${\bf B}_k$は、ヘッセ行列の近似に対応しており、最適性の２次の必要十分条件より、局所最適解が保証される。

セカント条件

　準ニュートン法では、正定値対称行列 ${\bf B}_k$を求める必要がある。

　まず、$f({\bf x_k})$ を ${\bf x}_{k+1}$ の周りで展開し

\begin{align}
f({\bf x}_k)\approx f({\bf x}_{k+1}) + {\bf \nabla} f({\bf x}_{k+1})({\bf x}_k-{\bf x}_{k+1})
\end{align}

２階微分可能とすれば、

\begin{align}
{\bf \nabla}f({\bf x}_k)\approx {\bf \nabla}f({\bf x}_{k+1}) + {\bf \nabla}^2 f({\bf x}_{k+1})({\bf x}_k-{\bf x}_{k+1})
\end{align}

となる。

　セカント条件は、${\bf \nabla}^2 f({\bf x}_{k+1})$ を正定値対称行列 ${\bf B} _{k+1}$ に置き換えた

\begin{align}
{\bf B} _{k+1}({\bf x}_{k+1}-{\bf x}_k)={\bf \nabla}f({\bf x}_{k+1})-{\bf \nabla}f({\bf x}_k) 
\end{align}

を満たす条件である。

　この条件を満たす ${\bf B} _{k}$ の更新式として、BFGS公式がある。

\begin{align}
{\bf B}_{k+1} &= {\bf B}_{k} - \frac{{\bf B}_{k}{\bf s}_k({\bf B}_{k}{\bf s}_k)^T } {{\bf s}_k^T {\bf B}_{k}{\bf s}_k} + \frac{{\bf y}_k({\bf y}_k)^T }{{\bf s}_k^T {\bf y}_k} \\
{\bf s}_k &= {\bf x}_{k+1} - {\bf x}_{k} \\
{\bf y}_k &= {\bf \nabla}f({\bf x}_{k+1})-{\bf \nabla}f({\bf x}_k) \\
\end{align}

${\bf B} _{k}$ が対称行列ならば、上式は対称行列なので　${\bf B} _{k+1}$ も対称行列となる。BFGS公式がセカント条件を満たすか確認すると

\begin{align}
{\bf B} _{k+1}({\bf x}_{k+1}-{\bf x}_k)&={\bf B} _{k+1} {\bf s}_k \\
&= {\bf B}_{k}{\bf s}_k - \frac{{\bf B}_{k}{\bf s}_k({\bf B}_{k}{\bf s}_k)^T } {{\bf s}_k^T {\bf B}_{k}{\bf s}_k}{\bf s}_k + \frac{{\bf y}_k({\bf y}_k)^T }{{\bf s}_k^T {\bf y}_k}{\bf s}_k            \\
&={\bf B}_{k}{\bf s}_k - \frac{{\bf B}_{k}{\bf s}_k } {{\bf s}_k^T {\bf B}_{k}{\bf s}_k} {\bf s}_k^T{\bf B}_{k}{\bf s}_k  +  \frac{{\bf y}_k }{{\bf s}_k^T {\bf y}_k} {\bf y}_k^T {\bf s}_k       \\
& = {\bf y}_k \\
&={\bf \nabla}f({\bf x}_{k+1})-{\bf \nabla}f({\bf x}_k) 
\end{align}

となり、BFGS公式がセカント条件を満たす。

正定値性

　BFGS公式は、セカント条件を満たし、更新された${\bf B} _{k+1}$ も対称行列となる。あとは、正定値であることを示す。

　まず、${\bf B} _{k}$ が正定値ならば ${\bf s}_k^T {\bf y}_k >0$ が成立することを示す。

　準ニュートン法で直線探索を行い

\begin{align}
g(\alpha_k) =f({\bf x}_{k+1})=f({\bf x}_k+\alpha_k {\bf d}({\bf x}_k))
\end{align}

が最小になるステップ幅$\alpha_k$ が求まったとする。このとき、

\begin{align}
\frac{\mathrm{d} g(\alpha) }{\mathrm{d} \alpha} &=\frac{\mathrm{d}  }{\mathrm{d} \alpha} f({\bf x}_k+\alpha {\bf d}({\bf x}_k)) \\
&= {\bf \nabla}  f({\bf x}_k+\alpha {\bf d}({\bf x}_k))^T \frac{\mathrm{d}  }{\mathrm{d} \alpha} ({\bf x}_k+\alpha {\bf d}({\bf x}_k)) \\
&= {\bf \nabla}  f({\bf x}_k+\alpha {\bf d}({\bf x}_k))^T {\bf d}({\bf x}_k)\\
&={\bf \nabla}  f({\bf x}_{k+1})^T {\bf d}({\bf x}_k) \\
&=0 
\end{align}

を満たすので、

\begin{align}
{\bf s}_k^T {\bf y}_k &= ({\bf x}_{k+1} - {\bf x}_{k})^T\left({\bf \nabla}f({\bf x}_{k+1})-{\bf \nabla}f({\bf x}_k)\right) \\
&= \alpha_k {\bf d}({\bf x}_k)^T{\bf \nabla}f({\bf x}_{k+1}) -\alpha_k {\bf d}({\bf x}_k)^T{\bf \nabla}f({\bf x}_k)\\
&=-\alpha_k {\bf d}({\bf x}_k)^T{\bf \nabla}f({\bf x}_k)\\
\end{align}

となる。準ニュートン法の探索方向を代入すれば、${\bf B} _{k}$が正定値なので、

\begin{align}
{\bf s}_k^T {\bf y}_k &=-\alpha_k {\bf d}({\bf x}_k)^T{\bf \nabla}f({\bf x}_k)\\
&=\alpha_k\left({\bf B}_k^{-1} \nabla f({\bf x}_k) \right)^T {\bf \nabla}f({\bf x}_k)\\
&=\alpha_k \nabla f({\bf x}_k) ^T{\bf B}_k^{-1}{\bf \nabla}f({\bf x}_k)>0\\
\end{align}

となる。（${\bf B} _{k}$は正定値対称行列なので、その逆行列も正定値になる。）

　
　最後に、${\bf B} _{k}$が正定値であるならば、行列${\bf B} _{k+1}$ も正定値であることを示す。任意のベクトル ${\bf u}$ を用意し

\begin{align}
{\bf u}^T{\bf B}_{k+1}{\bf u} &= {\bf u}^T{\bf B}_{k}{\bf u} - {\bf u}^T\frac{{\bf B}_{k}{\bf s}_k({\bf B}_{k}{\bf s}_k)^T } {{\bf s}_k^T {\bf B}_{k}{\bf s}_k}{\bf u} +{\bf u}^T \frac{{\bf y}_k({\bf y}_k)^T }{{\bf s}_k^T {\bf y}_k}{\bf u}\\
&={\bf u}^T{\bf B}_{k}{\bf u} -\frac{\left({\bf u}^T {\bf B}_{k}{\bf s}_k\right)^2}{{\bf s}_k^T {\bf B}_{k}{\bf s}_k} + \frac{\left( {\bf y}_k^T {\bf u}\right)^2}{{\bf s}_k^T {\bf y}_k}
\end{align}

を考える。${\bf u}^T{\bf B}_{k+1}{\bf u}>0$ ならば正定値である。

　${\bf B} _{k}$は正定値対称行列なので対角化できる。正則行列を${\bf P}$（${\bf P}^T{\bf P}={\bf I}$） とすれば、${\bf B} _{k}$は

\begin{align}
{\bf B}_{k}&= {\bf P}^T {\bf \lambda} {\bf P} = {\bf P}^T \sqrt{{\bf \lambda}} {\bf P} {\bf P}^T \sqrt{{\bf \lambda}}  {\bf P} = \bar{{\bf P} }^T\bar{{\bf P} }\\
\bar{{\bf P} } &={\bf P}^T \sqrt{{\bf \lambda}}  {\bf P}
\end{align}

と書ける。${\bf \lambda}$ は、対角上に固有値が並んだ行列である。上記の行列を使い、

\begin{align}
\bar{{\bf u}} =\bar{{\bf P} } {\bf u} 
\ \ , \ \ 
\bar{{\bf s}} =\bar{{\bf P} } {\bf s} 
\end{align}

と置くと、

\begin{align}
{\bf u}^T{\bf B}_{k+1}{\bf u} 
&={\bf u}^T\bar{{\bf P} }^T\bar{{\bf P}}{\bf u}
 -\frac{\left({\bf u}^T\bar{{\bf P} }^T\bar{{\bf P}} {\bf s}_k\right)^2}{{\bf s}_k^T\bar{{\bf P}}^T\bar{{\bf P}} {\bf s}_k}
 + \frac{\left( {\bf y}_k^T {\bf u}\right)^2}{{\bf s}_k^T {\bf y}_k}\\

&=\bar{{\bf u}}^T\bar{{\bf u}} -\frac{\left(\bar{{\bf u}}^T\bar{{\bf s}} \right)^2}{\bar{{\bf s}}^T\bar{{\bf s}}}+ \frac{\left( {\bf y}_k^T {\bf u}\right)^2}{{\bf s}_k^T {\bf y}_k}\\

&=\frac{\left(\bar{{\bf u}}^T\bar{{\bf u}}\right)\left(\bar{{\bf s}}^T\bar{{\bf s}}\right)-\left(\bar{{\bf u}}^T\bar{{\bf s}}\right)^2 }{\bar{{\bf s}}^T\bar{{\bf s}}}+ \frac{\left( {\bf y}_k^T {\bf u}\right)^2}{{\bf s}_k^T {\bf y}_k}
\end{align}

となる。

　シュワルツの不等式から

\begin{align}
\left(\bar{{\bf u}}^T\bar{{\bf u}}\right)\left(\bar{{\bf s}}^T\bar{{\bf s}}\right)\geq\left(\bar{{\bf u}}^T\bar{{\bf s}}\right)^2 
\end{align}

であり、さらに ${\bf s}_k^T {\bf y}_k >0$　が成立する。シュワルツの不等式において、等号を満たさない場合、

\begin{align}
{\bf u}^T{\bf B}_{k+1}{\bf u} 
&=\frac{\left(\bar{{\bf u}}^T\bar{{\bf u}}\right)\left(\bar{{\bf s}}^T\bar{{\bf s}}\right)-\left(\bar{{\bf u}}^T\bar{{\bf s}}\right)^2 }{\bar{{\bf s}}^T\bar{{\bf s}}}+ \frac{\left( {\bf y}_k^T {\bf u}\right)^2}{{\bf s}_k^T {\bf y}_k}\\
& > 0
\end{align}

である。

　シュワルツの不等式において、等号が成立する場合を考える。

\begin{align}
&\left(\bar{{\bf u}}^T\bar{{\bf u}}\right)\left(\bar{{\bf s}}^T\bar{{\bf s}}\right)=\left(\bar{{\bf u}}^T\bar{{\bf s}}\right)^2 \\
\end{align} 

等式を満たすには、$\eta(\neq0)$ を定数として

\begin{align}
\bar{{\bf u}} &= \eta \bar{{\bf s}} \\
\therefore \ \ \bar{{\bf P} } {\bf u}  &=\eta \bar{{\bf P} } {\bf s} \\
\therefore \ \  {\bf u}  &=\eta  {\bf s} 
\end{align} 

が成立すれば良い。このとき、

\begin{align}
{\bf u}^T{\bf B}_{k+1}{\bf u} 
&=\frac{\left(\bar{{\bf u}}^T\bar{{\bf u}}\right)\left(\bar{{\bf s}}^T\bar{{\bf s}}\right)-\left(\bar{{\bf u}}^T\bar{{\bf s}}\right)^2 }{\bar{{\bf s}}^T\bar{{\bf s}}}+ \frac{\left( {\bf y}_k^T {\bf u}\right)^2}{{\bf s}_k^T {\bf y}_k}\\
&= \eta ^2 \frac{\left( {\bf y}_k^T {\bf s}\right)^2}{{\bf s}_k^T {\bf y}_k}  \\
& > 0
\end{align}

となり、${\bf u}^T{\bf B}_{k+1}{\bf u} =0$ は満たさない。

よって、${\bf B} _{k}$が正定値であるならば、行列 ${\bf B} _{k+1}$ も正定値である。

　正定値対称行列の初期値は、

\begin{align}
{\bf B} _{0}={\bf I}
\end{align}

として計算される。　

記憶制限 BFGS 法

　BFGS 法の実装において、${\bf B}_{k}$ を記憶する必要があるため、大規模な計算の場合、メモリを多く必要とする。それを回避するため、記憶制限 BFGS 法　のアルゴリズムが使われる。

まずは、${\bf B}_{k+1}$ の逆行列を求める。

\begin{align}
{\bf B}_{k+1} &= {\bf B}_{k} - \frac{{\bf B}_{k}{\bf s}_k({\bf B}_{k}{\bf s}_k)^T } {{\bf s}_k^T {\bf B}_{k}{\bf s}_k} + \frac{{\bf y}_k({\bf y}_k)^T }{{\bf s}_k^T {\bf y}_k} \\
&= {\bf B}_{k} - 
\begin{pmatrix}
{\bf B}_{k}{\bf s}_k & {\bf y}_k \\
\end{pmatrix}

\begin{pmatrix}
-\frac{1}{{\bf s}_k^T {\bf B}_{k}{\bf s}_k} & 0 \\
0 &  \frac{1}{{\bf s}_k^T {\bf y}_k} \\
\end{pmatrix}

\begin{pmatrix}
({\bf B}_{k}{\bf s}_k)^T \\
({\bf y}_k)^T \\
\end{pmatrix} \\

\end{align}

逆行列の公式

\begin{align}
\left({\bf A}+ {\bf B}{\bf D}{\bf C} \right)^{-1}={\bf A}^{-1} -{\bf A}^{-1}{\bf B} \left( {\bf D}^{-1}+ {\bf C}{\bf A}^{-1}{\bf B} \right)^{-1}{\bf C}{\bf A}^{-1}
\end{align}

を使い、${\bf B_{k}}^{-1}={\bf H_{k}}$ と置き、${\bf B_{k}}$　は対称行列であることを使うと、

\begin{align}
{\bf H}_{k+1} &={\bf H}_{k}-{\bf H}_{k} 
\begin{pmatrix}
{\bf B}_{k}{\bf s}_k & {\bf y}_k \\
\end{pmatrix}
\left[
\begin{pmatrix}
-\frac{1}{{\bf s}_k^T {\bf B}_{k}{\bf s}_k} & 0 \\
0 &  \frac{1}{{\bf s}_k^T {\bf y}_k} \\
\end{pmatrix}^{-1}
+
\begin{pmatrix}
({\bf B}_{k}{\bf s}_k)^T \\
({\bf y}_k)^T \\
\end{pmatrix}
{\bf H}_{k} 
\begin{pmatrix}
{\bf B}_{k}{\bf s}_k & {\bf y}_k \\
\end{pmatrix}
\right]^{-1}
\begin{pmatrix}
({\bf B}_{k}{\bf s}_k)^T \\
({\bf y}_k)^T \\
\end{pmatrix}
{\bf H}_{k} \\

&={\bf H}_{k}-
\begin{pmatrix}
{\bf s}_k & {\bf H}_{k}{\bf y}_k \\
\end{pmatrix}
\left[
\begin{pmatrix}
-{\bf s}_k^T {\bf B}_{k}{\bf s}_k & 0 \\
0 &  {\bf s}_k^T {\bf y}_k \\
\end{pmatrix}
+
\begin{pmatrix}
({\bf B}_{k}{\bf s}_k)^T \\
({\bf y}_k)^T \\
\end{pmatrix}

\begin{pmatrix}
{\bf s}_k & {\bf H}_{k} {\bf y}_k \\
\end{pmatrix}
\right]^{-1}
\begin{pmatrix}
({\bf s}_k)^T \\
({\bf y}_k)^T {\bf H}_{k}\\
\end{pmatrix}
\end{align}

また、

\begin{align}
&\left[
\begin{pmatrix}
-{\bf s}_k^T {\bf B}_{k}{\bf s}_k & 0 \\
0 &  {\bf s}_k^T {\bf y}_k \\
\end{pmatrix}
+
\begin{pmatrix}
({\bf B}_{k}{\bf s}_k)^T \\
({\bf y}_k)^T \\
\end{pmatrix}

\begin{pmatrix}
{\bf s}_k & {\bf H}_{k} {\bf y}_k \\
\end{pmatrix}
\right]^{-1}
\\
&=
\begin{pmatrix}
-{\bf s}_k^T {\bf B}_{k}{\bf s}_k+{\bf s}_k^T {\bf B}_{k}{\bf s}_k & {\bf s}_k^T {\bf y}_k \\
{\bf y}_k^T {\bf s}_k &  {\bf s}_k^T {\bf y}_k +{\bf y}_k^T{\bf H}_{k} {\bf s}_k \\
\end{pmatrix}^{-1}
\\
&=-\frac{1}{({\bf s}_k^T {\bf y}_k )({\bf y}_k^T {\bf s}_k)}
\begin{pmatrix}
{\bf s}_k^T {\bf y}_k +{\bf y}_k^T{\bf H}_{k} {\bf s}_k & -{\bf s}_k^T {\bf y}_k \\
-{\bf y}_k^T {\bf s}_k &  0 \\
\end{pmatrix}

\end{align}

となるため、

\begin{align}
{\bf H}_{k+1} 
&={\bf H}_{k}+\frac{1}{({\bf s}_k^T {\bf y}_k )({\bf y}_k^T {\bf s}_k)}
\begin{pmatrix}
{\bf s}_k & {\bf H}_{k}{\bf y}_k \\
\end{pmatrix}

\begin{pmatrix}
{\bf s}_k^T {\bf y}_k +{\bf y}_k^T{\bf H}_{k} {\bf s}_k & -{\bf s}_k^T {\bf y}_k \\
-{\bf y}_k^T {\bf s}_k &  0 \\
\end{pmatrix}

\begin{pmatrix}
({\bf s}_k)^T \\
({\bf y}_k)^T {\bf H}_{k}\\
\end{pmatrix}
\\
&={\bf H}_{k}+\frac{1}{({\bf s}_k^T {\bf y}_k )({\bf y}_k^T {\bf s}_k)}\left\{
{\bf s}_k ({\bf s}_k^T {\bf s}_k ){\bf s}_k^T 
+{\bf s}_k {\bf y}_k^T {\bf H}_{k}{\bf y}_k{\bf s}_k^T
-{\bf s}_k({\bf s}_k^T{\bf y}_k) {\bf y}_k^T{\bf H}_{k}
-{\bf H}_{k}{\bf y}_k({\bf y}_k^T{\bf s}_k){\bf s}_k^T\right\}
\end{align}

よって、${\bf B_{k+1}}$ の逆行列 ${\bf H_{k+1}}$

\begin{align}
{\bf H}_{k+1}&=\left({\bf I}-\frac{{\bf s}_k({\bf y}_k)^T}{{\bf y}_k^T{\bf s}_k }\right) {\bf H}_{k} \left({\bf I}-\frac{{\bf y}_k({\bf s}_k)^T}{{\bf y}_k^T{\bf s}_k }\right)+
\frac{{\bf s}_k({\bf s}_k)^T}{{\bf y}_k^T{\bf s}_k }
\end{align}

が求まる。

　${\bf H}_{k+1}$ を分解することを考える。

\begin{align}
{\bf v}_k = {\bf I} - \rho_k {\bf y}_k{\bf s}_k^T 
\ \ , \ \
\rho_k = \frac{1}{{\bf y}_k^T{\bf s}_k}
\end{align}

とおき、計算ステップ $k$ ごとに　${\bf H}_{k}$ 分解していき

\begin{align}
{\bf H}_{k+1}&={\bf v}_k^T{\bf H}_{k}{\bf v}_k+ \rho_k {\bf s}_k{\bf s}_k^T \\
&={\bf v}_k^T\left\{ {\bf v}_{k-1}^T{\bf H}_{k-1}{\bf v}_{k-1}+ \rho_k {\bf s}_{k-1}{\bf s}_{k-1}^T\right\}{\bf v}_k+ \rho_k {\bf s}_k{\bf s}_k^T \\
&=({\bf v}_k^T{\bf v}_{k-1}^T){\bf H}_{k-1}({\bf v}_{k-1}{\bf v}_{k})
+\rho_k {\bf v}_k^T{\bf s}_{k-1}{\bf s}_{k-1}^T{\bf v}_k
+ \rho_k {\bf s}_k{\bf s}_k^T \\
&\vdots \\
&=({\bf v}_k^T{\bf v}_{k-1}^T\cdots {\bf v}_{0}^T){\bf H}_{0}({{\bf v}_{0}\cdots\bf v}_{k-1}{\bf v}_{k})
+\rho_0 ({\bf v}_k^T{\bf v}_{k-1}^T\cdots {\bf v}_{1}^T){\bf s}_{0}{\bf s}_{0}^T ({{\bf v}_{1}\cdots\bf v}_{k-1}{\bf v}_{k}) \\
&+\cdots+\rho_k {\bf v}_k^T{\bf s}_{k-1}{\bf s}_{k-1}^T{\bf v}_k
+ \rho_k {\bf s}_k{\bf s}_k^T
\end{align}

となる。

　記憶制限 BFGS 法は、過去の $m$ ステップ分だけ情報を保持し

\begin{align}
{\bf H}_{k+1}&=({\bf v}_k^T{\bf v}_{k-1}^T\cdots {\bf v}_{k-m}^T){\bf H}_{０}({{\bf v}_{k-m}\cdots\bf v}_{k-1}{\bf v}_{k})\\
&+\rho_{k-m} ({\bf v}_k^T{\bf v}_{k-1}^T\cdots {\bf v}_{k-m+1}^T){\bf s}_{k-m}{\bf s}_{k-m}^T ({{\bf v}_{k-m+1}\cdots\bf v}_{k-1}{\bf v}_{k}) \\
&+\cdots+\rho_k {\bf v}_k^T{\bf s}_{k-1}{\bf s}_{k-1}^T{\bf v}_k
+ \rho_k {\bf s}_k{\bf s}_k^T
\end{align}

を計算する。

　記憶制限 BFGS 法のアルゴリズムは、wikipedia に記載されている。

　

参考文献

記事は、以下の書籍を参考にしています。

しっかり学ぶ数理最適化　モデルからアルゴリズムまで
梅谷俊治・著