概要
土木業界において、画像分類およびセマンティックセグメンテーションのAIは、様々な所で適応されています。特に、よく使われる画像、航空写真や地形画像などは、高解像度の画像である場合が多いです。
高解像度の画像で分類問題を解きたい、またそこで深層学習を使いたい場合、画像のサイズを小さくして(リスケールして)学習・推論を行う場合があります。ただし、画像サイズを小さくしてしまうと、画像分類に寄与する情報を失ってしまう場合があります。
他に、医療画像などから病気を発見し、その病気の箇所を知りたい場合、セマンティックセグメンテーションのAIがよく用いられます。しかし、アノテーションのデータセットの作成は、労力がかかります。
今回の記事では、Attention を使った Deep Multiple Instance Learningについて説明します。高解像度の画像を小さいサイズ(例えば 32x32 ピクセル)の画像に分割し、MIL(Multiple Instance Learning) を使い2値分類を行います。Attention を使いMILを構築し、Attention を可視化することで、画像のどの箇所が分類に寄与するかわかります。
(すなわち説明可能AIで、医療画像の場合、Attention を可視化することで、病気の箇所をアノテーションぽく囲ってくれることを期待する。)
論文は以下を引用しています。
Keras のブログでも紹介されています。この記事を参考にプログラムを構築できます。
日本語の記事では、以下のアドレスで紹介されています。
MIL(Multiple Instance Learning)
最初に、MILについて説明する。
MIL の学習は、1つのクラスに割り当てられた instance の bag を取り扱う。MIL の目的として、bag のラベルを予測することである。この記事において、bag は分割された画像の集合であり、instance とは分割した個々の画像である。
\begin{align}
&\text{label variable} \ \ y \in \{0,1\} \\
&\text{instance } \ \ x \in \mathbb{R} \\
&\text{ K 分割された bag } \ \ X = \{x_1,x_2,\ldots,x_K \} \\
\end{align}
以下の図は、4分割した場合の例である。
instance には個々のラベル {$y_1,y_2,\ldots,y_K$} が存在し、bag のラベル $Y$ は、
Y =
\begin{cases}
0 & {\displaystyle\sum_{k=1}^K y_k }=0 \\
1 & \text{else}
\end{cases}
と書ける。MILは、permutation invariant であるので、つまり、$K$ 分割された bag $X =$ {$x_1,x_2,\ldots,x_K $} の順番に依らないので(順番を入れ替えても同じ結果にならないといけない)
\begin{align}
Y = \max_k \{y_k \}
\end{align}
と書き直せる。実装では、instance の個々のラベルは知る必要がなく、分割する前の画像のラベルが分かればよい。
MILの誤差関数は、(bag のラベルに従う)ベルヌーイ分布から得られた対数尤度関数を最適化する。つまり、クロスエントロピーを用いる。このときのベルヌーイ分布のパラメータを $\theta(X) \in [0,1]$ とする。 $\theta(X)$ は、instance の bag $X =$ {$x_1,x_2,\ldots,x_K $} が与えられたとき、$Y=1$ となる確率である。
deep MIL
次に、ニューラルネットワークを用いたMILについて説明する。
$K$ 個の instance $x_k$ を、ニューラルネットワーク $f_{\psi}$ を使い低次元に埋め込むことを考える(次元圧縮)。
\begin{align}
h_k = f_{\psi}(x_k)
\end{align}
\begin{align}
\text{ K 個の埋め込まれた bag} \ \ & H = \{h_1,h_2,\ldots,h_K \} \\
\end{align}
MIL で重要な点としては、permutation invariant である。つまり、埋め込まれた $K$ 個の instance $(h_1,h_2,\ldots,h_K ) $ の順番を入れ替えても不変でなければならない。permutation invariant になるように MIL pooling が必要である。
よく使われる MIL pooling は、$h_k$ が $M$次元のベクトルとして、maximum 演算子
\begin{align}
z_m = \max_{k=1,\ldots,K}\{h_{km} \}
\end{align}
mean 演算子
\begin{align}
z_m = \frac{1}{K}{\displaystyle\sum_{k=1}^K h_{km} }
\end{align}
がよく使われる。
ベルヌーイ分布のパラメータを $\theta(X)$ は、ニューラルネットワークと MIL pooling によって得られた値 $z$ と $g_{\phi}$ を使い決定する。つまり、$g_{\phi}$ は深層学習でよく使われる分類器である。
Attention based MIL pooling
最後に、Attention を用いた MIL pooling について説明する。
Attention を用いた MIL pooling は、$V,W$ は学習で決定するパラメータとして
\begin{align}
z &= {\displaystyle\sum_{k=1}^K a_k h_{k} } \\
a_k &= \frac{\exp\left\{W^T\tanh\left(Vh_k^T\right)\right\} }{{\displaystyle\sum_{j=1}^K}\exp\left\{W^T\tanh\left(Vh_j^T\right)\right\} }
\end{align}
で計算される。この計算により、instance 間の類似度(または非類似度)を見つけることが目的である。($a_kh_k$ の足し算の順番を変えても同じ結果になるので、permutation invariant になっている。)
さらに複雑な表現を得るために、シグモイド関数(数式内でsigm)を使い、$U,V,W$ は学習で決定するパラメータとして
\begin{align}
z &= {\displaystyle\sum_{k=1}^K a_k h_{k} } \\
a_k &= \frac{\exp\left\{W^T\left(\tanh\left(Vh_k^T\right)\bigodot \mbox{sigm}\left(Uh_k^T\right) \right) \right\} }{{\displaystyle\sum_{j=1}^K}\exp\left\{W^T\left(\tanh\left(Vh_j^T\right)\bigodot \mbox{sigm}\left(Uh_j^T\right) \right) \right\} }
\end{align}
とする。$\bigodot $ はアダマール積である。
Attention を用いた MIL pooling のコードは以下のように書けるだろう(Keras のチュートリアルとほぼ同じ)。
# ------------------------------------------------------
# Attention based MIL pooling
# ------------------------------------------------------
class MILAttentionLayer(tf.keras.layers.Layer):
def __init__(self,input_dim,weight_params_dim,kernel_initializer="glorot_uniform",
kernel_regularizer=None,**kwargs,):
super().__init__(**kwargs)
self.weight_params_dim = weight_params_dim
# 重みの初期化
self.kernel_initializer = tf.keras.initializers.get(kernel_initializer)
# 重みの正則化
self.kernel_regularizer = tf.keras.regularizers.get(kernel_regularizer)
self.v_init = self.kernel_initializer
self.w_init = self.kernel_initializer
self.u_init = self.kernel_initializer
self.v_regularizer = self.kernel_regularizer
self.w_regularizer = self.kernel_regularizer
self.u_regularizer = self.kernel_regularizer
# attention で使う weight
self.v = self.add_weight(shape=(input_dim, self.weight_params_dim),
initializer=self.v_init,name="v",regularizer=self.v_regularizer,trainable=True,)
self.u = self.add_weight(shape=(input_dim, self.weight_params_dim),
initializer=self.u_init,name="u",regularizer=self.u_regularizer,trainable=True,)
self.w = self.add_weight(shape=(self.weight_params_dim, 1),
initializer=self.w_init,name="w",regularizer=self.w_regularizer,trainable=True,)
def call(self, inputs):
# attention score の計算
instances=tf.TensorArray(tf.float32, size=FLAGS.BAG_SIZE)
# instance ごとに処理
for i in range(FLAGS.BAG_SIZE):
instances=instances.write(i, self.compute_attention_scores(inputs[i]) )
instances=instances.stack()
# instance ごとに softmax で正規化
alpha = tf.math.softmax(instances, axis=0)
return alpha
def compute_attention_scores(self, instance):
original_instance = instance
# tanh(v*h_k^T)
instance = tf.math.tanh(tf.tensordot(original_instance, self.v, axes=1))
instance = instance * tf.math.sigmoid(tf.tensordot(original_instance, self.u, axes=1))
# w^T*(tanh(v*h_k^T)*sigmoid(u*h_k^T))
return tf.tensordot(instance, self.w, axes=1)
MNIST bags の結果
まずは、手書き文字のデータセットであるMNIST を使い、分類できるか、Attention は妥当かどうか検証する。
ニューラルネットワーク $f_{\psi}$ は、簡単な畳み込みニューラルネットワークを使用した。(Keras のブログでは畳み込みは使用していない。)
# ------------------------------------------------------
# 簡単な畳み込み
# ------------------------------------------------------
class CnnLayer(tf.keras.layers.Layer):
def __init__(self,**kwargs,):
super().__init__(**kwargs)
# kaiming He らの初期化
self.He_init = tf.keras.initializers.HeNormal()
self.conv1 =tf.keras.layers.Conv2D(32, (3, 3), activation='relu', kernel_initializer=self.He_init)
self.maxp1 =tf.keras.layers.MaxPooling2D((2, 2))
self.conv2 =tf.keras.layers.Conv2D(64, (3, 3), activation='relu', kernel_initializer=self.He_init)
self.maxp2 =tf.keras.layers.MaxPooling2D((2, 2))
self.conv3 =tf.keras.layers.Conv2D(64, (3, 3), activation='relu', kernel_initializer=self.He_init)
def call(self,x):
x = self.conv1(x)
x = self.maxp1(x)
x = self.conv2(x)
x = self.maxp2(x)
x = self.conv3(x)
return x
ランダムに MNIST 画像を16枚選び構成した画像を1つの bag としてデータを作成する。ランダムに選んだ16枚の画像のうち、手書き文字 $0$ が含まれているなら positive class 、つまり、 bag のラベル $Y=1$ とする。その他は、Negative class 、bag のラベル $Y=0$ とする。
例えば、以下の左画像は、positive class とし、 右画像は、Negative class とした。
 |
 |
学習曲線は、以下の通りになった。誤差関数の値も収束し、正答率もほぼ100%である。
 |
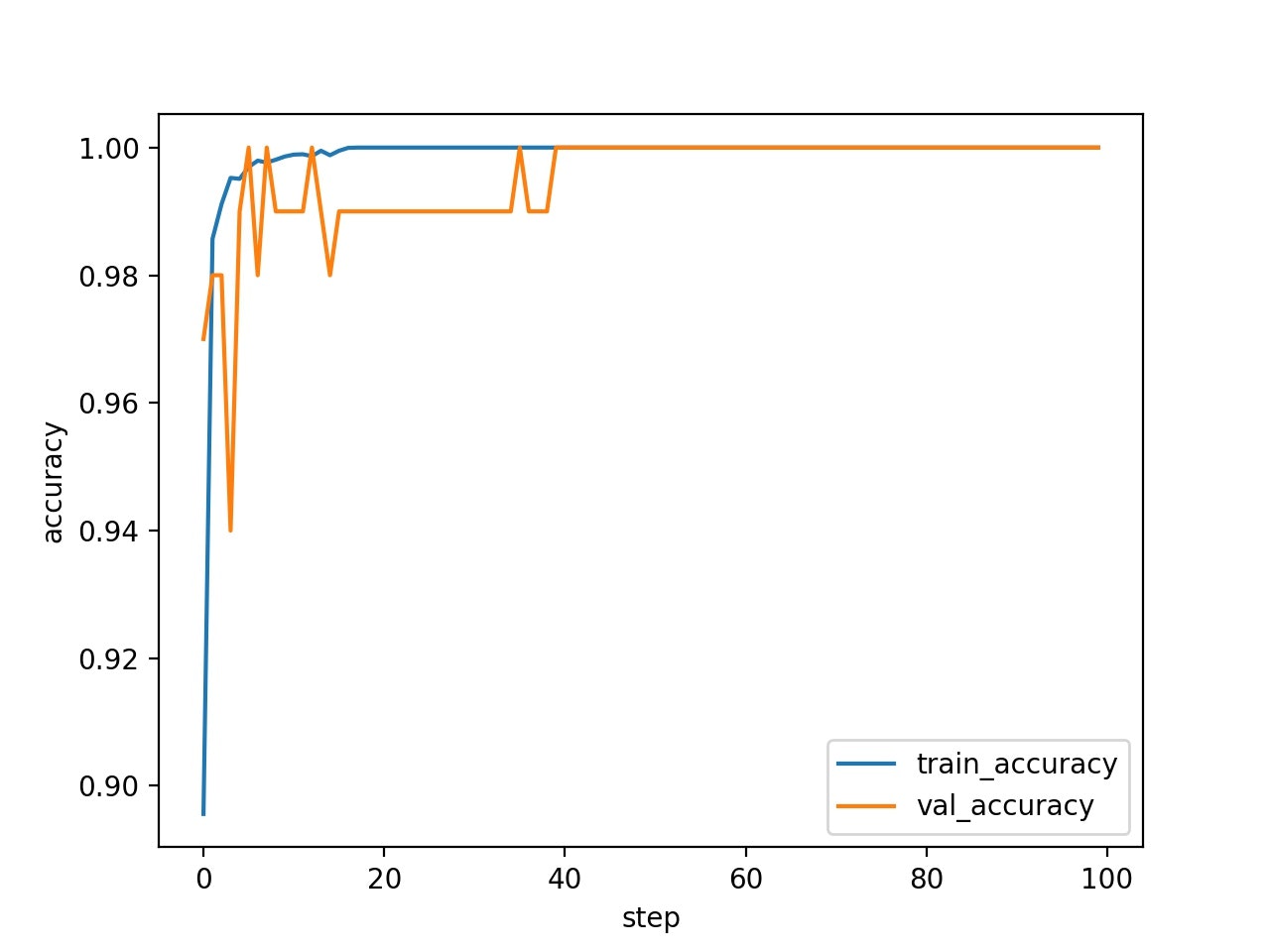 |
次に、positive class (bag の中に手書き文字$0$ が含まれているclass)のAttention の値を確認すると、手書き文字$0$の instance の、Attention の値が高くなっていることが分かる。
 |
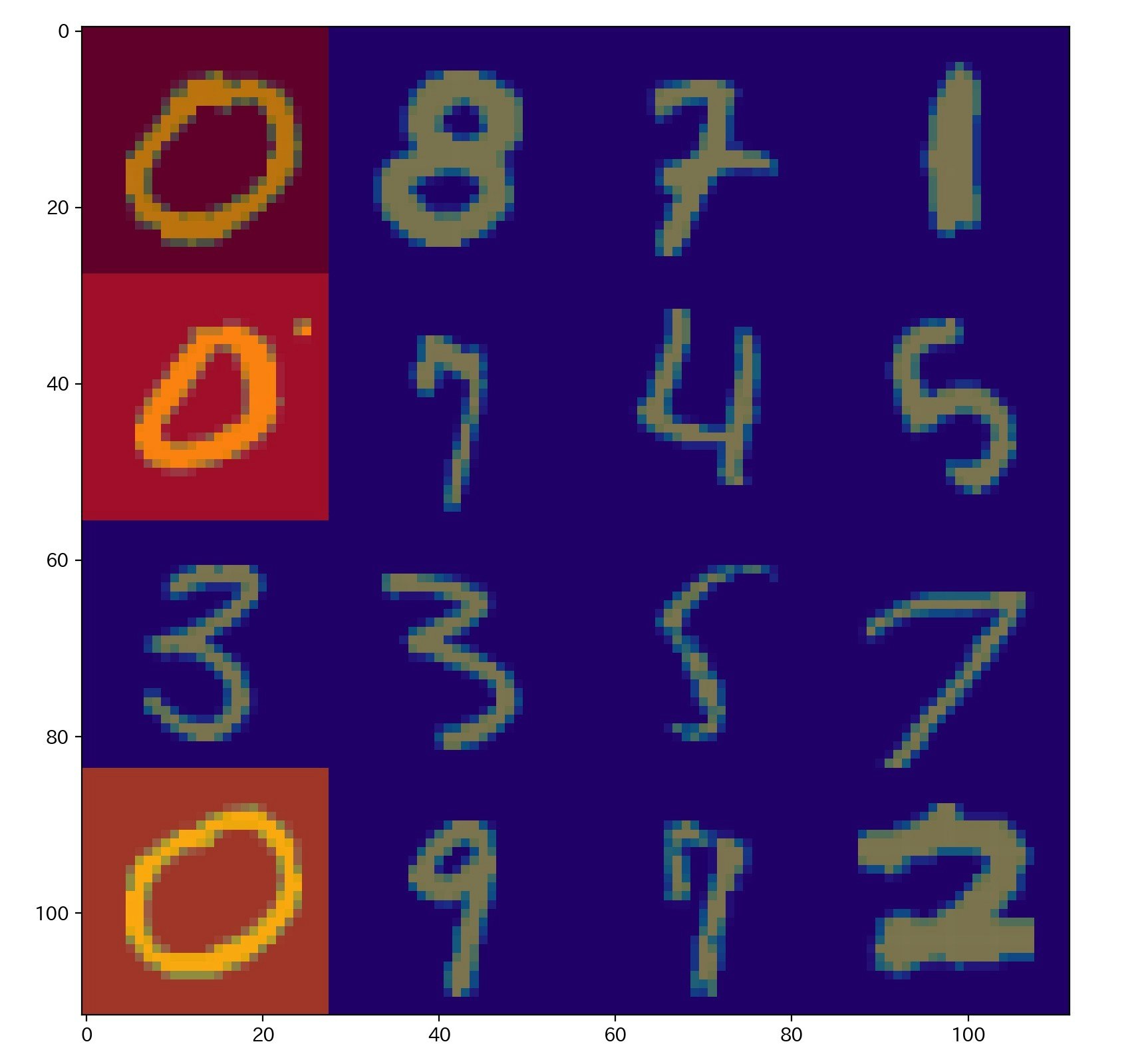 |
 |
Attention の値は、min-max 変換を行っている。
\begin{align}
a_k \leftarrow \frac{a_k - \min(a_k)}{\max(a_k)-\min(a_k)}
\end{align}
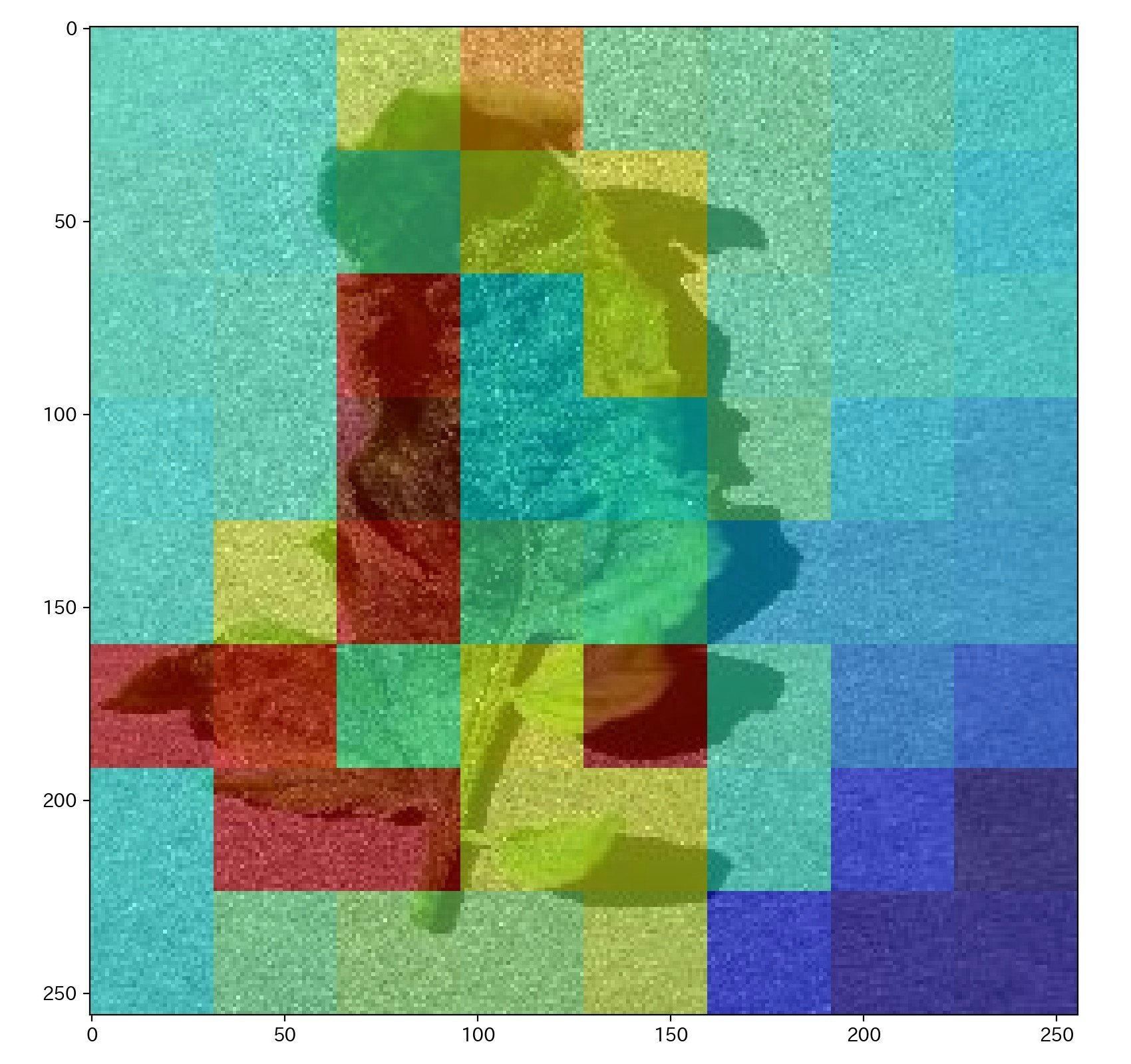
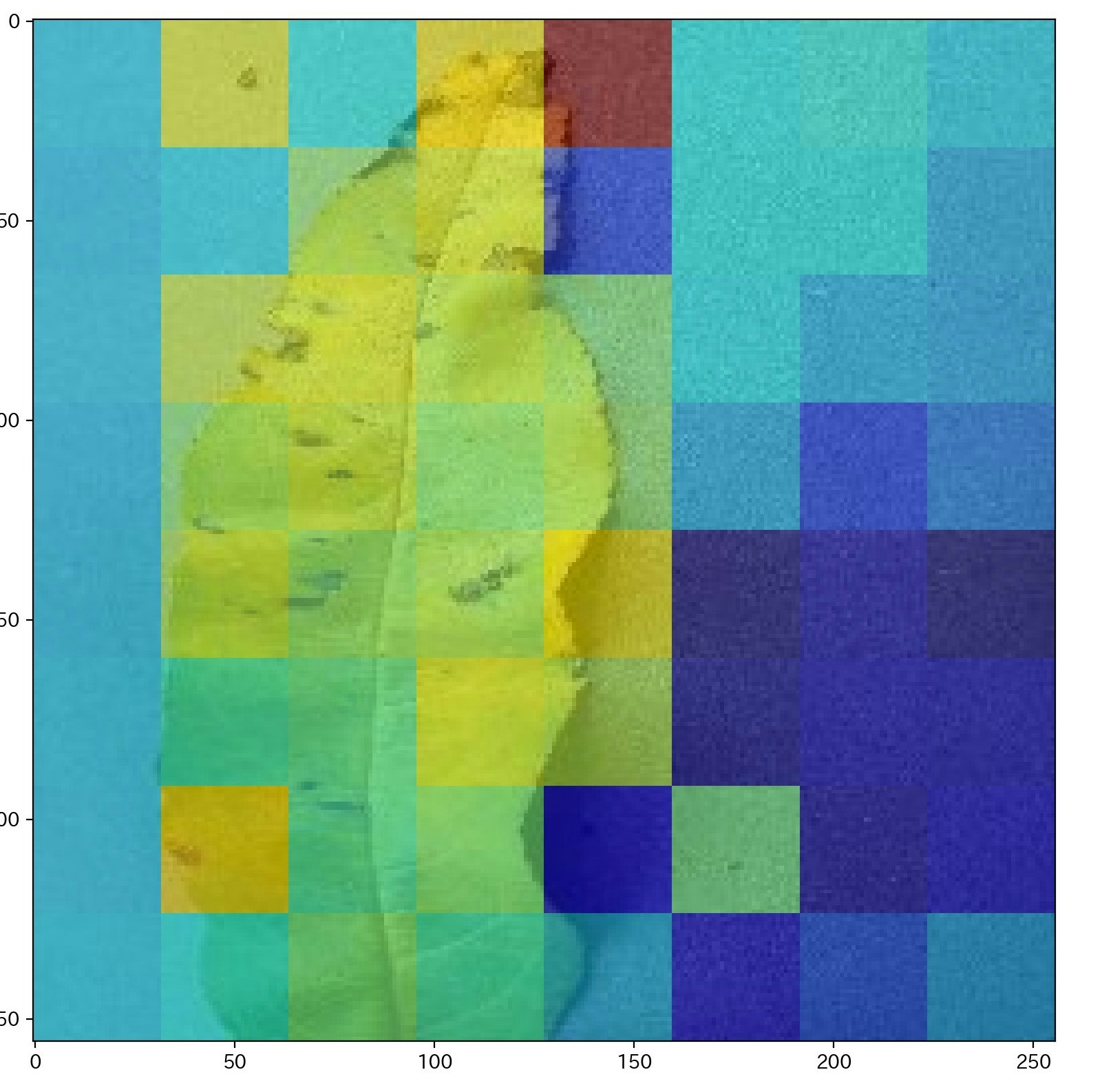
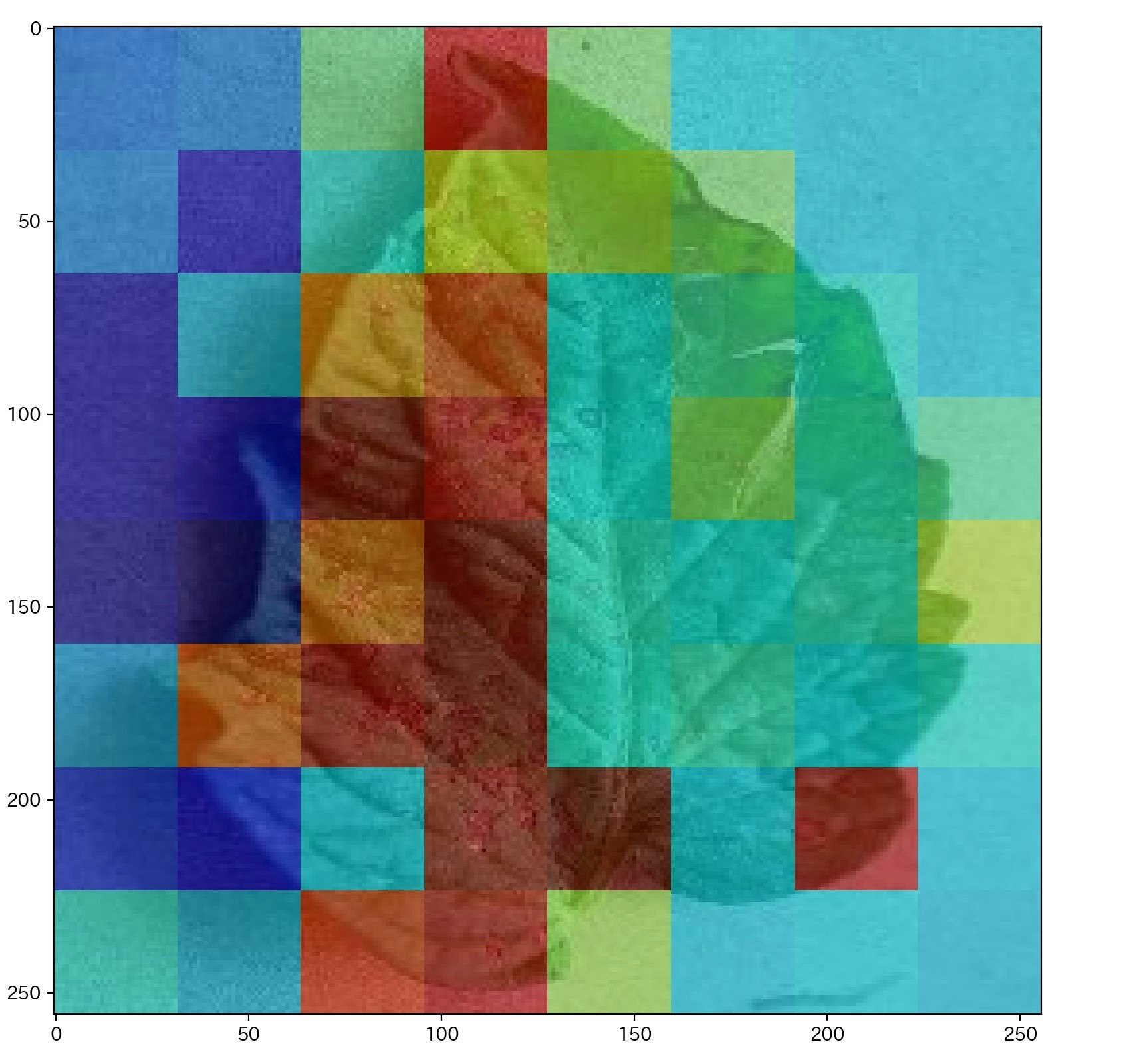
plant_village bags の結果
Tensorflow から取得できる以下のアドレスの、葉っぱの病気のデータを使い学習を行った。
ニューラルネットワーク $f_{\psi}$ は、MNIST bags と同様に、簡単な畳み込みニューラルネットワークを使用した。
画像サイズは、256x256 ピクセルで、画像を64枚に分割した。葉っぱの種類とその病気で分類されており、全部で38クラスある。この記事では、病気か健康か、2値分類として、学習をおこなった。
クラス名に healthy がついていたら Negative class(bag のラベル $Y=0$)、その他は positive class (bag のラベル $Y=1$)とした。
データ数は全部で54303枚であるが、trainデータは20000枚、validationデータは500枚としている。
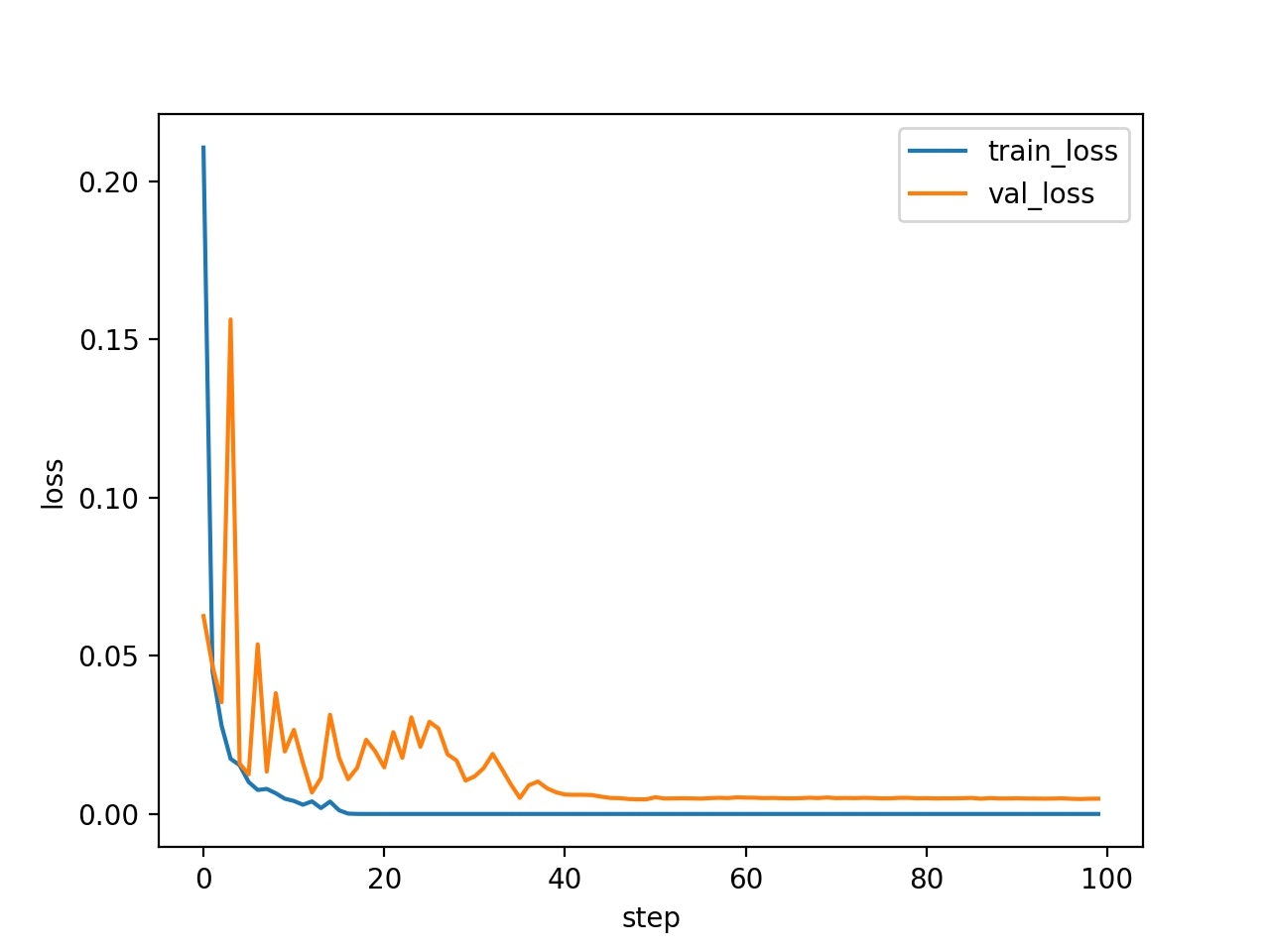
学習曲線は、以下の通りになった。誤差関数の値も収束している。
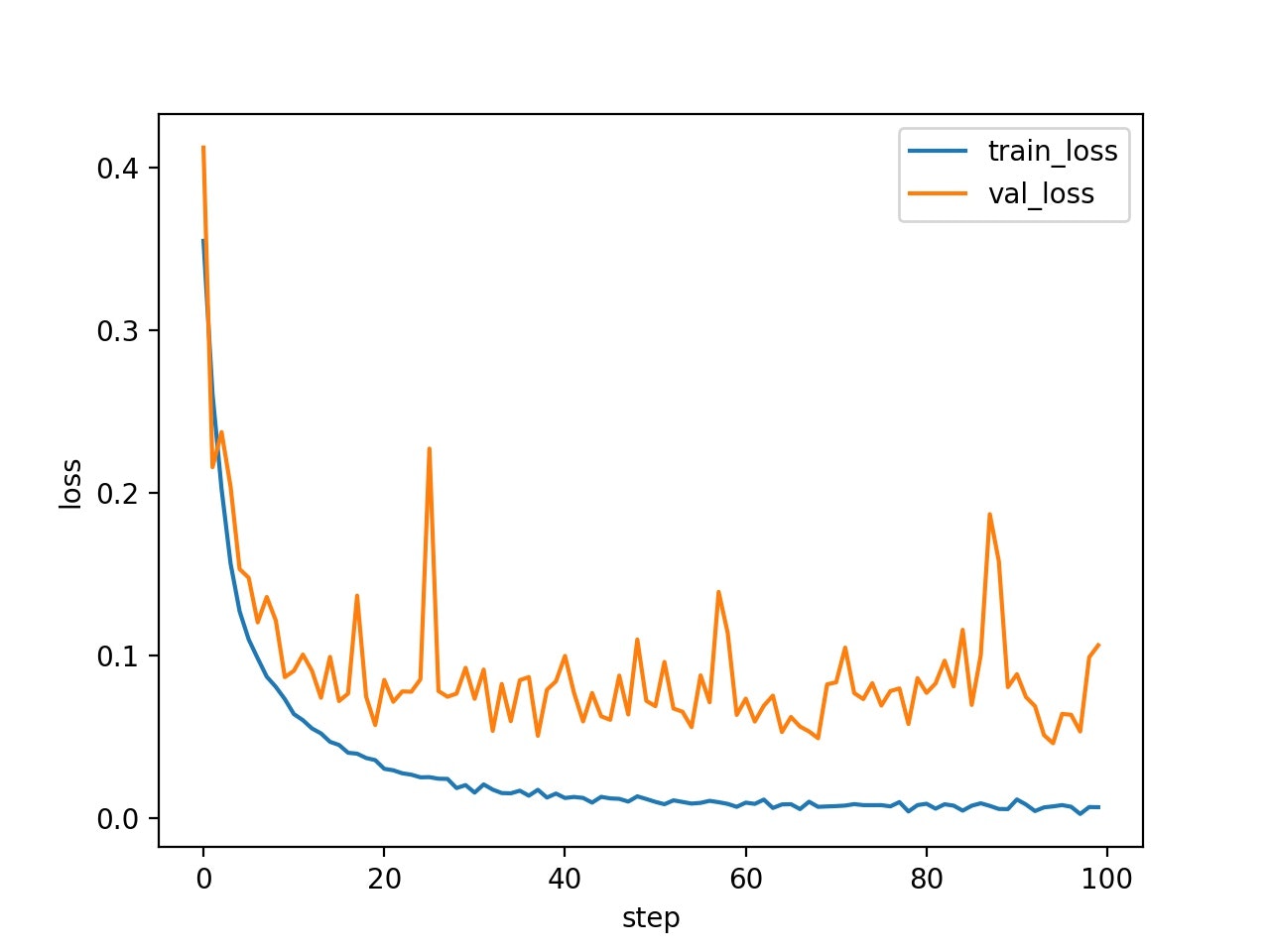 |
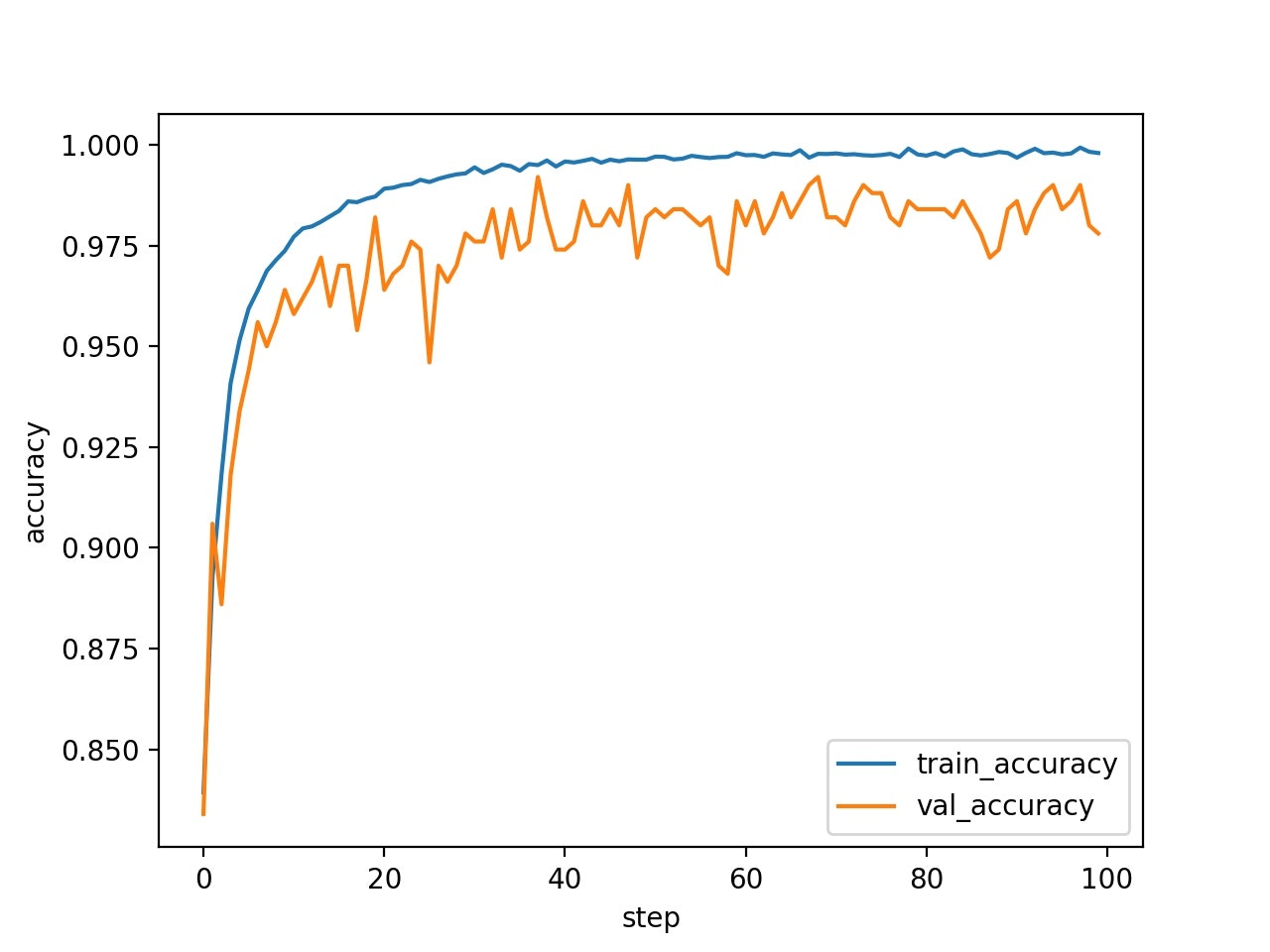 |
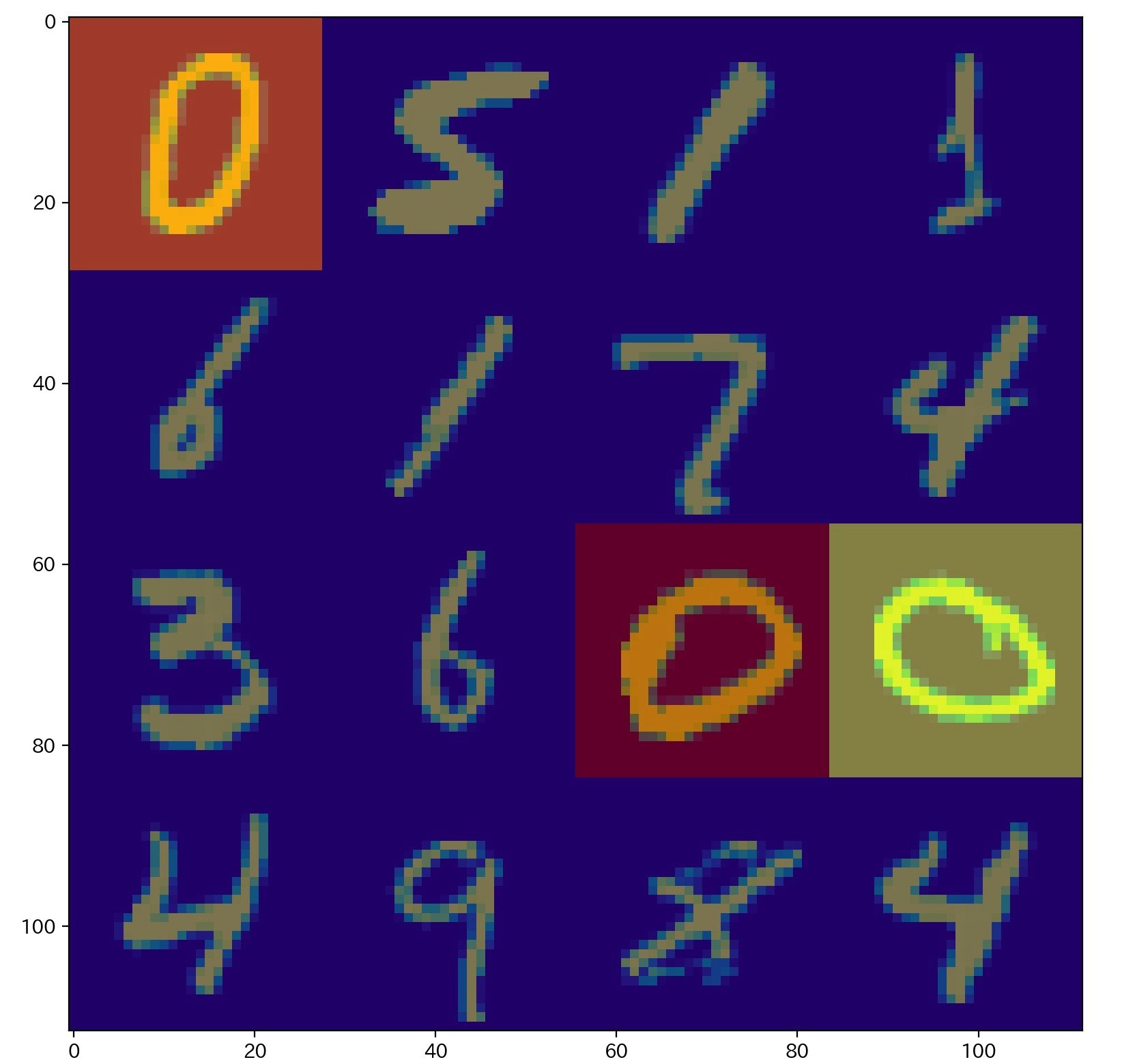
次に、positive class (病気のデータ)のAttention の値を確認すると、病気っぽいところの instance の、Attention の値が高くなっていると思われる。Attention の値は、min-max 変換を行っている。
まとめ
MNIST データとplant_villageを使い、学習をおこなった。ただし、画像サイズは小さいサイズである。論文では、896x768 ピクセルの医療系のデータセットを使っている。今後は、1000x1000 ピクセルのようなデータで試す必要がある。(もう少しアノテーション的な感じにしたい。)