概要
土木の分野において、道路や橋梁のひび割れ・破損を物体検知の手法を取り入れられ、様々な場面で適用されています。
通常の教師ありの物体検知では、精度を上げるにはデータが多く必要であり、人間がアノテーションをするのにかなりの労力が必要となります。また、土木分野において、普通の人間では認識が難しいデータセット(例えば、航空写真を使った地形データなど)では、そもそも教師あり学習データが正しいかどうか、判断が難しい場合があります。このような場合、教師無し物体検知が有用だと考えています。
話は逸れて、自然言語処理や画像分類において、注意機構(Attention)が使われています。Attentionは、AIがどこを見て判断しているか説明(解釈)するために有用だと注目を集めています。個人的には、Attentionの技術にとても注目しています。
今回の記事では、Slot Attentionを用いた教師無しの物体検知(Object Discovery)について紹介します。また参考にした論文に集合予測について書かれていたので、それについても簡単に紹介したいと思います。
Slot Attention をつかった反復Attentionメカニズム(iterative attention mechanism)は、潜在表現から入力の特徴マップを分解し、グループ分けの手順(grouping strategy)を学習します。つまり、それぞれのスロットで1つの物体を記述することができます。
今回の論文で、はじめて教師無し物体検知・物体中心表現・集合予測を勉強したので、間違っている点が多々あると思います。
論文は以下を引用しています。
またtensorflowのコードが公開されています。
日本語の解説として、以下の解説があります。論文の理解に、とても役立ちました。
物体中心表現については、以下を引用しています。
物体中心表現
人間が物体を認識するとき、人間の目(網膜)は、3次元の拡がりを持った物体を認識しているのではなく、3次元を2次元に射影したものを認識している。網膜は、奥行きの情報が欠如していても、物体を認識できる。
機械学習に与える入力データも人間と同じ情報のはずである。しかし、日当たり・影などが変化しても人間は認識できるが、機械学習は、日当たり・影などをの影響を受けてしまい、学習が上手くいかないことが頻繁に起こる。
「畳み込み」と「プーリング」によって構成される畳み込みニューラルネットワーク(CNN)は、ヒューベルとウィーゼルの仮設に基づき構築された数理モデルである。畳み込み層は局所的な特徴を抽出し、プーリング層は物体の移動に対して不変となるように導入する。(カプセルネットワークでは、プーリング層に関して否定的である。今回の記事で登場するCNNは、プーリング層は入れない。)
CNNは、知覚特徴量は抽出できるが、日当たり・影などをの影響についての不変性は考慮されていない。
Marrらは「物体の内部表現は、網膜像の変化に関して不変であり(物体が暗くなったり、近くまた遠くなったりしても影響は受けないと言うこと)、その表現は物体中心である三次元表現である。」と考えた。このことを物体中心表現と呼ぶ(のだろう)。
物体中心表現を獲得することで、2次元情報から3次元情報を推論することができる。Slot attentionは、物体中心表現を獲得するためのアルゴリズムである。
他の表現方法として、分散表現がある。詳しくは理解していないが、分散表現は教師あり物体検知などで使われ、埋め込みベクトルを学習させる方法である。
Attention
Attention に関しては、多数の分かりやすい記事があるので、大雑把に説明する。
Attention は辞書オブジェクトと呼ばれている。例えば、Key を[1,2,3]とし Key に対応する要素(Value)を [a,b,c] とする。辞書は
辞書={1 : a , 2 : b, 3 : c}
みたいになる。Query とは、検索したい Key なので、例えば、Query を 1 とすると
辞書[1] = a
となり、1 の要素(Value)a が取り出せる。もちろん、Query は Key に含まれなければ Value は取り出せない。
Attention(正確にはDot Product Attention)は、Key , Query , Value と呼ばれるLayer がある。AI のなかでは、Key と Query は一致しない。したがって、Key と Query の内積、つまり類似度を計算しSoftmax関数で正規化する。これを、Attentoin Weightと呼ばれる。Attentoin Weight に Value を作用させることで値を取り出す。
単純な例を考えてみる。Key を
K=
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
とし対応する Value を
V=
\begin{pmatrix}
a\\
b\\
c\\
\end{pmatrix}
とする。つまり、Key の$(1\ \ 0\ \ 0)$は Value の $a$ に対応し、同様に、$(0\ \ 1\ \ 0)$は $b$ 、$(0\ \ 0\ \ 1)$は $c$ に対応する。
Queryが
Q=
\begin{pmatrix}
0.8 & 0.2 & 0.0
\end{pmatrix}
だったとする。この Query は、Key の$(1\ \ 0\ \ 0)$に類似しているため、Attentionを計算すると Value の中の $a$ が取り出せそうである。
Attention weight を計算してみると(簡単なためSoftmax正規化は行わない)
W=QK^T=\begin{pmatrix}
0.8 \\
0.2 \\
0.0 \\
\end{pmatrix}
Attention は
\mbox{attn} = W^TV = 0.8*a+0.2*b
と求まり、a に近い値が取り出せる(もちろん a,b,c の大きさにも依るが)。
実際のAIでは、 Key , Query , Value の値は学習により決定する。
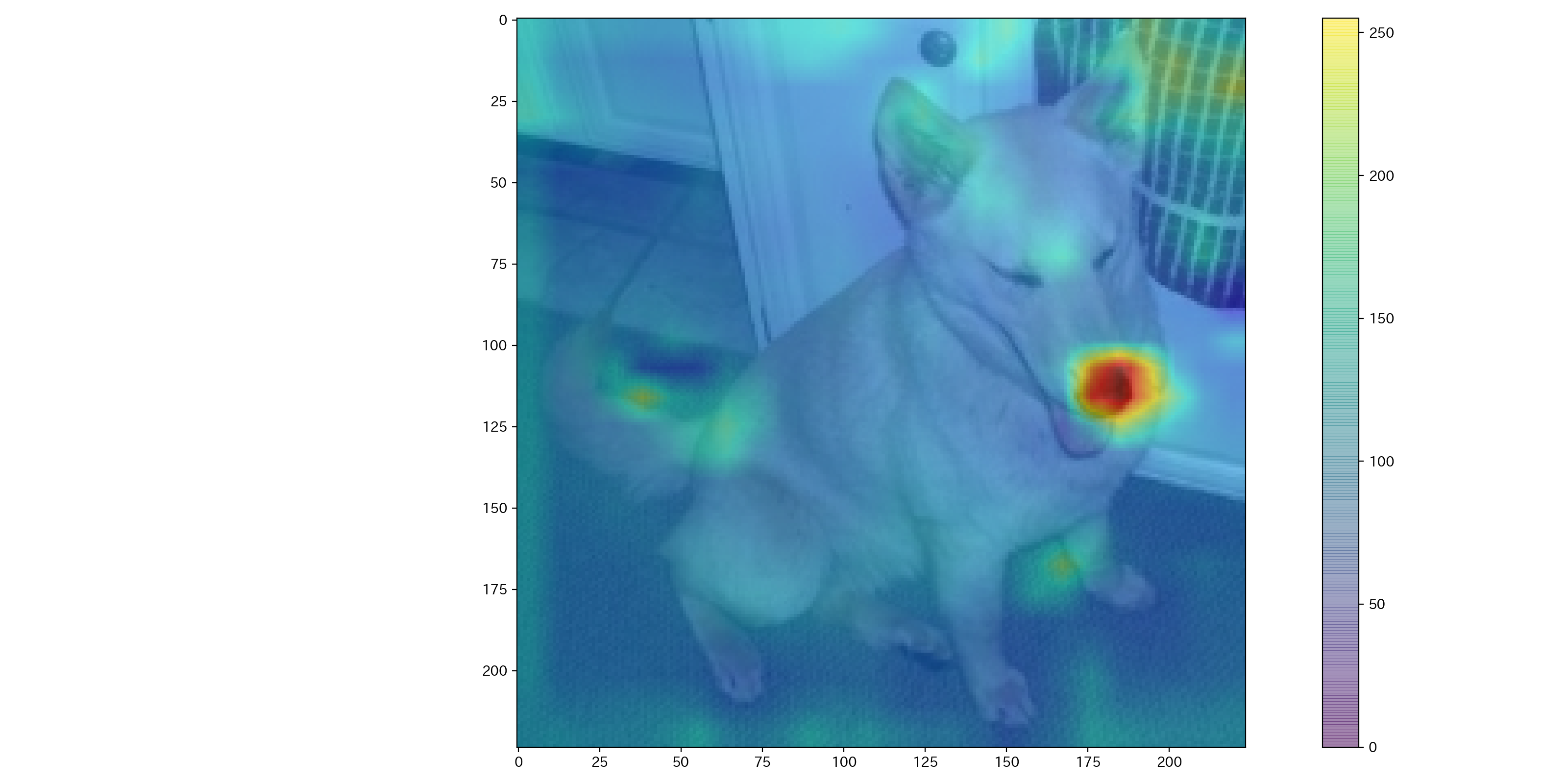
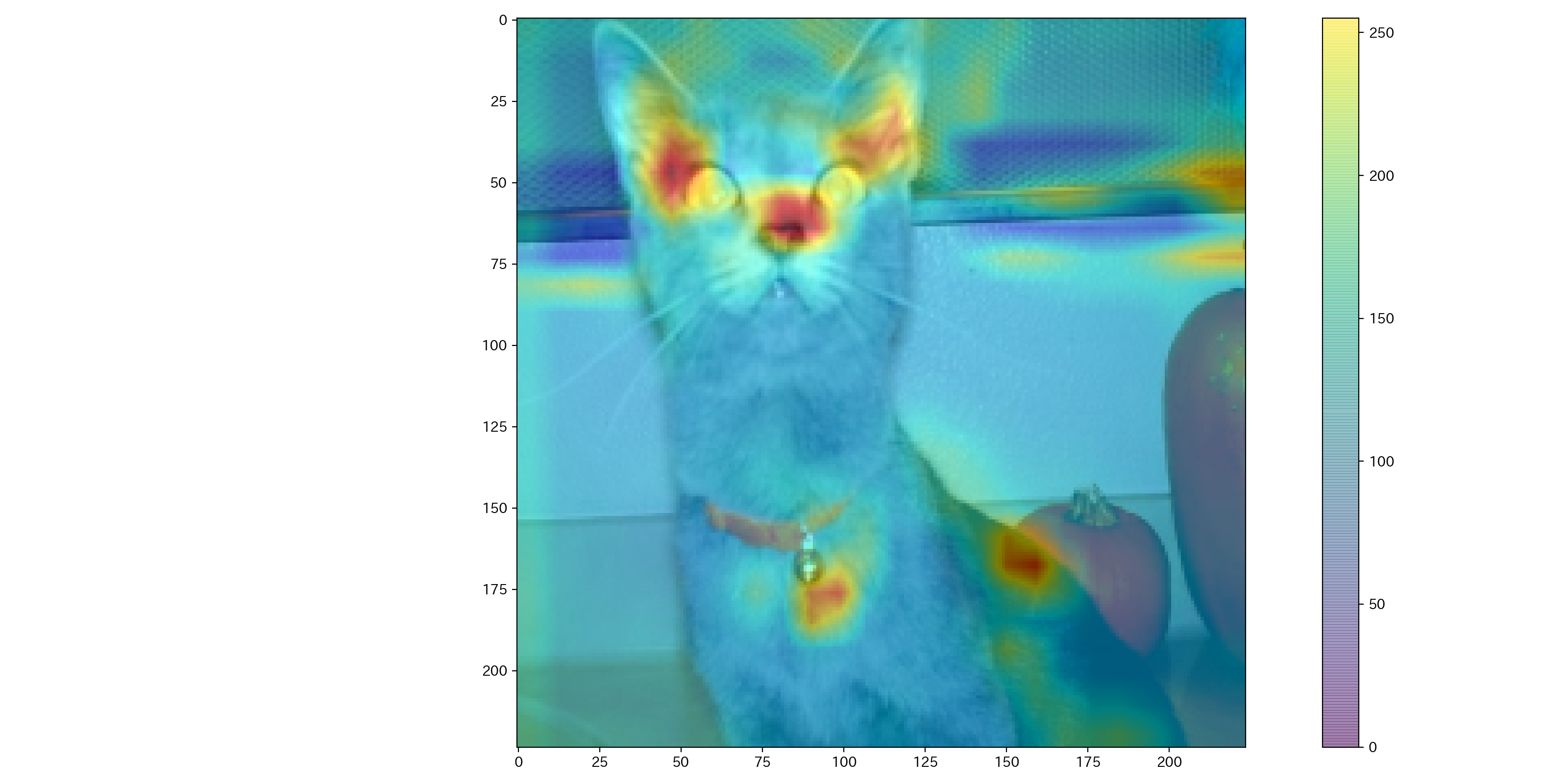
Attentionは、AIがどこを見て判断しているか説明(解釈)するために有用だと考えられている。例えば、画像分類を考え、Value を画像の値(または、畳み込みによって得られた特徴量)とすると、Attention weight と Value の計算は、画像に分類に寄与する部分だけ取り出すことを意味するだろう。Attention weight は、Softmax関数で正規化されているので、Attention weight が1に近い要素は、分類に寄与する要素と考えることができ、逆に0に近い要素は分類に寄与しない要素だと考えることができる。
この記事では、詳細に説明はしないが、CNN + Attentionのネットワークを使い、犬・猫分類を行い、Attention weight をプロットすると以下の画像ようになる。何となく、耳や鼻、目などに注目してそうである。
Slot attention
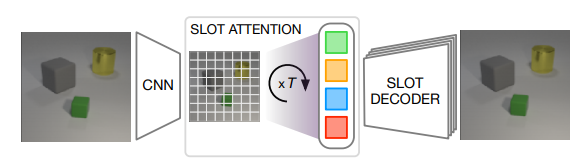
Slot attentionのアルゴリズムは以下の図である。以下の図は、論文から引用している。

最初に、画像をCNNに入力して、畳み込み後のサイズ$W,H$として、特徴量 $\mathrm{R}^{W\times H\times D_{input},}$を出力させる。特徴量を平坦化させ、特徴マップ $\mathrm{R}^{N\times D_{input},}$を Slot Attentionの入力とする。
Slotは、ガウス分布$\mathcal{N}(\mu,\mbox{diag}(\sigma))$から$k$個サンプルする。また、$\mu\in\mathrm{R}^{D_{slot}}$と$\sigma\in\mathrm{R}^{D_{slot}}$は平均・分散である。ガウス分布のパラメータ$\mu,\sigma$も学習させる。
$Q,K,V$をQuery・Key・Valueとする。Softmax Temperature $T=\sqrt{D_{slot}}$として、attentionをQueryとKeyを使い
\begin{align}
\mbox{attn}_{i,j}&=\mbox{softmax}(M)_{i,j} =\frac{\exp\{M_{i,j}\}}{\sum_l \exp\{M_{i,l}\}} \\
M&=\frac{1}{\sqrt{D_{slot}}}K(\mbox{inputs})Q^T(\mbox{slots}) \in \mathrm{R}^{N\times k}
\end{align}
とする。Softmax Temperature は内積が大きくならないようにする。Attention Weightは、正規化を行い
\begin{align}
W_{i,j}=\frac{\mbox{attn}_{i,j}}{\sum_l \mbox{attn}_{i,l}}
\end{align}
Slotは、Attention Weight と Value の積とする。
\begin{align}
\mbox{slot}=W^T V(\mbox{inputs}) \in \mathrm{R}^{k\times D_{slot} }
\end{align}
Slotの値を(ゲート付き)再帰ニューラルネットワーク(GRU)を使い、Slotを更新する。
Slot Attentionの意味は、$k$個のSlotが、入力された特徴マップが物体なのか空なのか記述する。Attention のKeyとValueは特徴マップを入力とするが、QueryはSlotを入力とする。Queryを反復させることでSlotは、入力された特徴マップの1部を解釈できるようになり、物体中心表現をもつ潜在表現を獲得することができる(らしい)。
各スロットは、物体の一部のみの情報を保持しており、それらをまとめてデコードすれば元の画像に復元することができる。
集合予測に関する簡単な説明
今回の集合予測では、画像内に写っている複数の物体の情報を予測する。CLEVR dataset においては、物体の有無(True, False)、サイズ(small, large)、物性(metal, rubber)、形状(cube, sphere, cylinder)、色(gray, blue, brown, yellow, red, green, purple, cyan)、位置(x, y, z)を予測する。
上記のような集合予測の機械学習アルゴリズムは、置換不変(permutation invariance)または置換同変(permutation equivariance)でなければならない。
一般的な機械学習アルゴリズムは、入力データが配列となっており、その配列を入れ替えれば予測結果は変わる。例えば、画像や時系列データは、入力データの配列を入れ替えるとデータの意味が変わるので、置換不変・置換同変である必要がなく、一般的な機械学習アルゴリズムが使用できる。
集合タイプのデータは、入力データの配列を入れ替えてもデータの意味が変わらないので、入力データを変えても予測結果が変わらないようなアルゴリズム、つまり、置換不変および置換同変なアルゴリズムが必要である。
例えば、AIを$f$、集合タイプの入力データを$[A,B,C]$、出力を$\alpha$とすると、置換不変なAIは、
\begin{align}
[A,B,C] &\xrightarrow[f]{} [\alpha] \\
[A,C,B] &\xrightarrow[f]{} [\alpha] \\
& \vdots \\
[C,B,A] &\xrightarrow[f]{} [\alpha] \\
\end{align}
を満たす必要があり、入力データ$[A,B,C]$を入れ替えても出力結果は変わらない。
上記の関係は、関数 $f:\mathrm{R}^{M\times D_1} \rightarrow \mathrm{R}^{M\times D_2} $ として、置換行列を$\pi \in \mathrm{R}^{M\times M}$とすれば、
\begin{align}
f(\pi x) = f(x)
\end{align}
と書ける。
また、AIを$f$、集合タイプの入力データを$[A,B,C]$、出力を$[\alpha,\beta,\gamma ]$とすると、置換同変なAIは、
\begin{align}
[A,B,C] &\xrightarrow[f]{} [\alpha,\beta,\gamma ] \\
[A,C,B] &\xrightarrow[f]{} [\alpha,\gamma,\beta ] \\
& \vdots \\
[C,B,A] &\xrightarrow[f]{} [\gamma,\beta,\alpha ] \\
\end{align}
を満たす必要があり、入力データ$[A,B,C]$を入れ替えたら、出力結果$[\alpha,\beta,\gamma ]$も入れ替わる。
上記の関係は、関数 $f:\mathrm{R}^{M\times D_1} \rightarrow \mathrm{R}^{M\times D_2} $ として、置換行列を$\pi \in \mathrm{R}^{M\times M}$とすれば、
\begin{align}
f(\pi x) = \pi f(x)
\end{align}
と書ける。
Slot Attention は置換同変なアルゴリズムであり、以下の命題が成立する。
命題
$\mbox{input} \in \mathrm{R}^{N\times D_{input}}$ と $\mbox{slots}\in \mathrm{R}^{K\times D_{slots}}$ 、そして、Slot Attention の出力を $\mbox{Slot Attention}(\mbox{inputs},\mbox{slots}) \in \mathrm{R}^{K\times D_{slots}}$ とする。
$\mbox{input}$ に対する置換行列を $\pi_i\in\mathrm{R}^{N\times N}$ 、$\mbox{slots}$ に対する置換行列を $\pi_s\in\mathrm{R}^{K\times K}$ とする。
このとき、
\begin{align}
\mbox{Slot Attention}(\pi_i \cdot \mbox{inputs},\pi_s\cdot\mbox{slots}) &= \pi_s\cdot\mbox{Slot Attention}(\mbox{inputs},\mbox{slots})
\end{align}
が成立する。
Slot attention のアルゴリズムに含まれる Key,Quary,Value および LayerNorm そしてGRU は、入力($\mbox{input}$および$\mbox{slots}$)に対して線形な Layer またはアルゴリズムなので置換同変である。
Attention は、
\begin{align}
\mbox{softmax}(\pi_s\cdot\pi_i \cdot M)_{k,l} &=\frac{\exp\{(\pi_s\cdot\pi_i \cdot M)_{k,l}\}}{\sum_j \exp\{(\pi_s\cdot\pi_i \cdot M)_{k,j}\}} \\
& = \frac{\exp\{ M_{\pi_i(k),\pi_s(l)}\}}{\sum_j \exp\{M_{\pi_i(k),\pi_s(j)}\}} \\
& = \mbox{softmax} (M)_{\pi_i(k),\pi_s(l)}
\end{align}
となるので、置換同変である。
Attention Weightは、置換同変であり
\begin{align}
W_{\pi_i(k),\pi_s(l)} =\frac{ \mbox{softmax} (M)_{\pi_i(k),\pi_s(l)}}{\sum_j \mbox{softmax} (M)_{\pi_i(k),\pi_s(j)}}
\end{align}
Slotは、Attention Weight と Value の積であり
\begin{align}
\mbox{slot}_{\pi_s(l)}=\sum_k W_{\pi_i(k),\pi_s(l)} V(\mbox{inputs})_{\pi_i(k)}
\end{align}
添え字 $k$ について足し上げるので、$\mbox{input}$ に対する置換行列 $\pi_i$ に関して置換不変、$\mbox{slots}$ に対する置換行列$\pi_s$に関して置換同変である。
すべてのステップにおいて置換同変なので、命題の
\begin{align}
\mbox{Slot Attention}(\pi_i \cdot \mbox{inputs},\pi_s\cdot\mbox{slots}) &= \pi_s\cdot\mbox{Slot Attention}(\mbox{inputs},\mbox{slots})
\end{align}
が成立する。
画像内に写っている物体の情報を入れ替えたら、出力結果も入れ替わってほしい。Slot の役割は、画像に写っている物体の一部の情報を保持する役割を持っている。写っている物体の情報を入れ替えるとは、Slot を入れ替えることである。Slot Attention は、Slot を入れ替えたら出力結果も入れ替わるアルゴリズムになっている。
物体検知および集合予測のネットワーク構成
物体検知(Object Discovery)のネットワークの構成について説明する。図は論文から引用した。
物体検知は、エンコーダー・デコーダーからなり、さらにエンコーダーは2つのネットワークからなる。
(1). CNNにより、知覚特徴量を抽出する。位置情報を把握するために、CNNから得られた特徴量にpositional embedding を行う。
(2). Slot Attention により物体中心表現を獲得する。
デコーダに関しては、Slot から二次元グリッドを作成する。(tf.tileを使い(1,1) -> (width, height)にする。)次にCNNを使いデコードして、最終的な画像出力サイズを、Slotごとに$W\times H\times 4$とする。この出力をRGBの画像$W\times H\times 3$とmask $W\times H\times 1$に分解する。msak は、Softmax関数を使い正規化する。各Slotまとめて mask とRGBの画像を結合して再構成画像を出力させる。誤差関数は、自乗誤差を使う。
次に集合予測のネットワークの構成について説明する。図は論文から引用した。
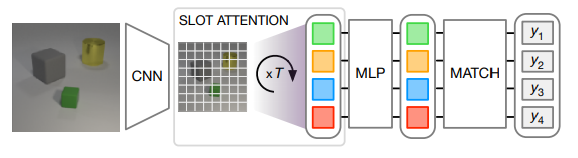
最初の部分は、物体検知と同じエンコーダーを用いる。エンコーダーの次に分類用のニューラルネットを追加する。ただし出力次元は、Slot数を$k$として $\mbox{batch}\times k\times \mbox{set classes}$ とする。
誤差関数は、hangarian loss を使う。hangarian loss は、予測集合 $\hat{Y}=[\hat{y}_1,\hat{y}_2,\ldots,\hat{y}_n ]$とtarget(正解) 集合 $Y=[{y}_1,{y}_2,\ldots,{y}_n ]$として
\begin{align}
\mathcal{L}_{hun}(\hat{Y},Y) = \min_{\pi \in \Pi} \|\hat{y}_i - y_{\pi(i)} \|
\end{align}
である。$\pi$は置換を意味する。
教師無し物体検知の結果
バッチサイズは16、Slot の数は7、再帰ニューラルネットの繰り返し数は3として学習させた。学習ステップ数は500000であり、論文と比べると(論文のバッチサイズは64?)バッチサイズが小さいので、学習ステップ数が足りない結果になったと考えられる。計算時間は約5日かかった。
学習率の変化は、指数関数的減衰させた。学習率は0.0004であるが、10000ステップまで Warm-up させる。
# 学習率の変化
def lr_scheduling(base_learning_rate,global_step,warmup_steps,decay_rate,decay_steps):
# Learning rate warm-up
if global_step < warmup_steps:
learning_rate = base_learning_rate * tf.cast(global_step, tf.float32) / tf.cast(warmup_steps, tf.float32)
else:
learning_rate = base_learning_rate
# Learning rate の減衰
learning_rate = learning_rate * (decay_rate ** (
tf.cast(global_step, tf.float32) / tf.cast(decay_steps, tf.float32)))
return learning_rate.numpy()
以下の図を確認すると、誤差が順調に下がっていることが分かる。
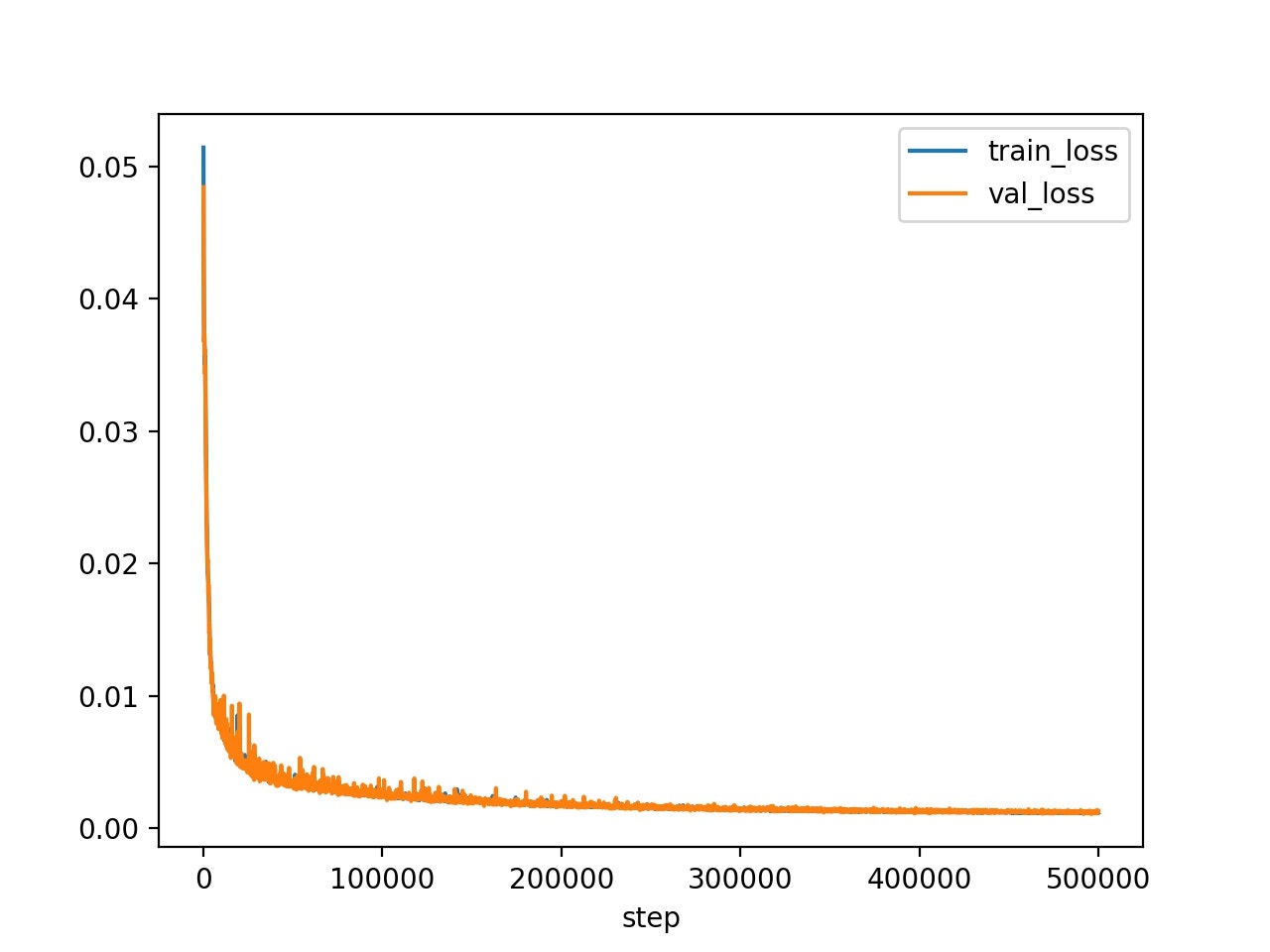
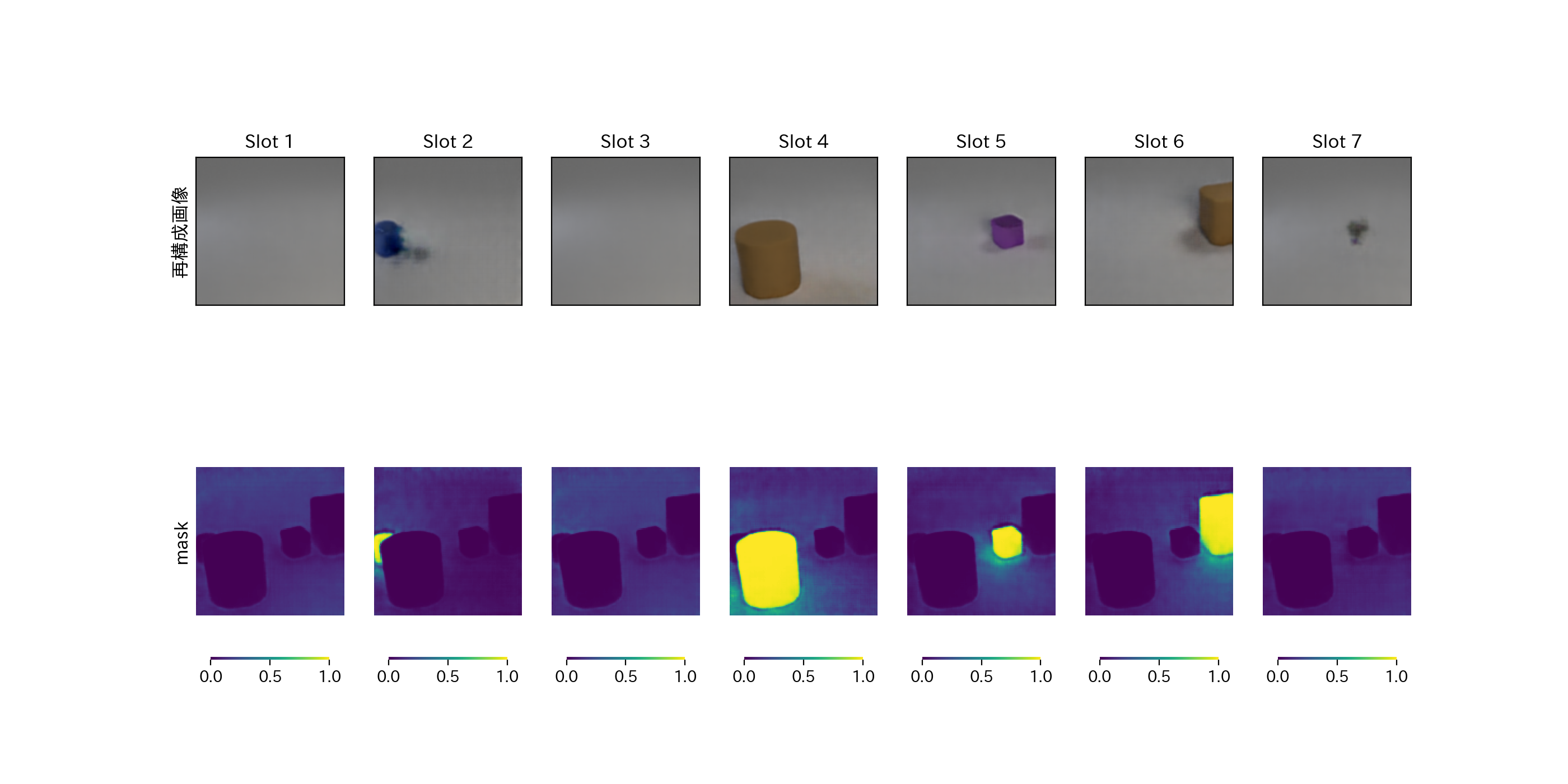
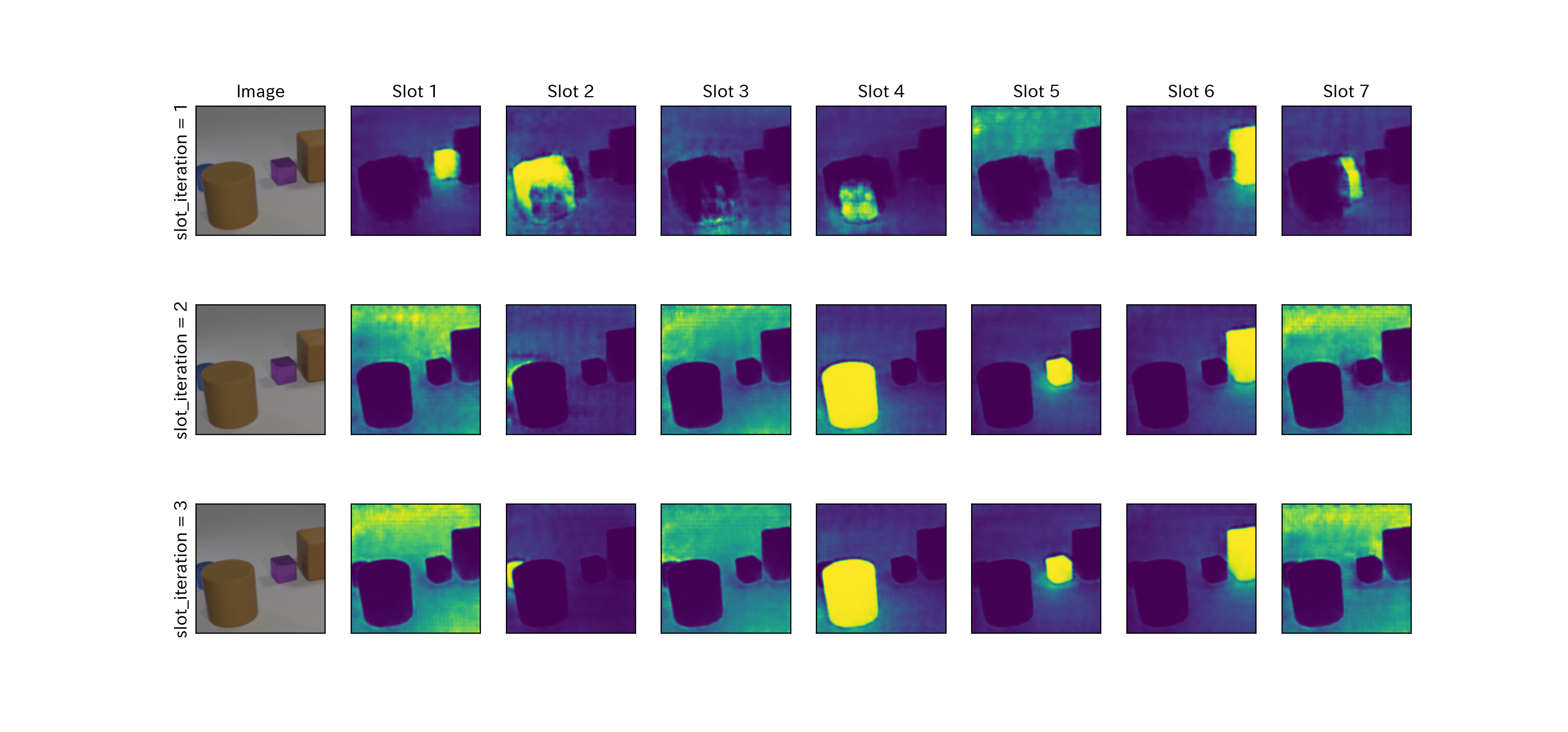
物体検知の結果を見ると、Slot ごとに物体を検知できていることが確認でき、物体がないところは空になるように記述されている。
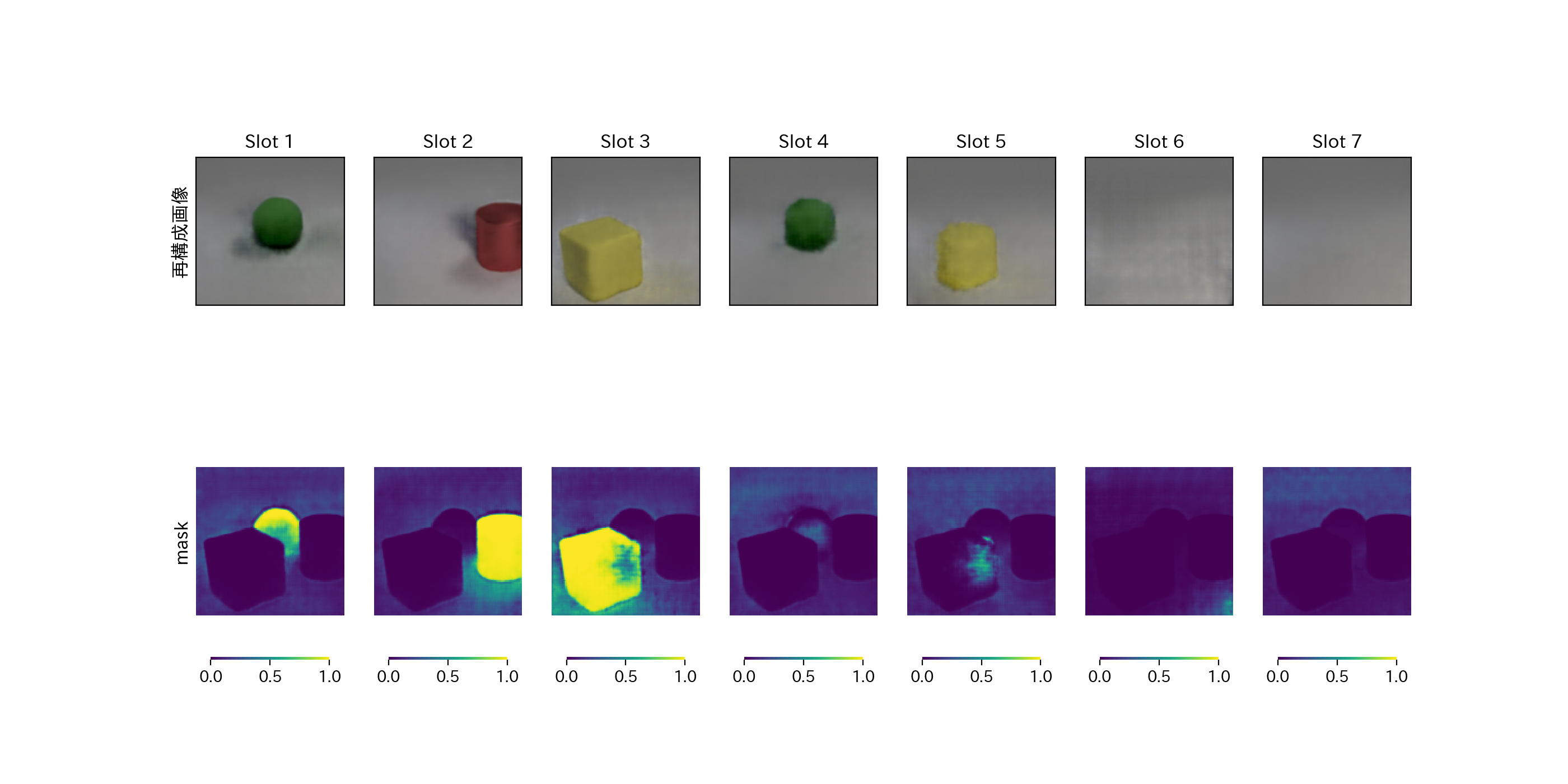
次に、デコーダの出力画像を見てみる。slotごとに$W\times H\times 4$が出力され、この出力をRGBの画像$W\times H\times 3$ と mask $W\times H\times 1$に分解されている。概ねSlot ごとに一部の情報が再構成され、mask もそれに反応していることが分かる。図の mask は、都合上(カラーbarを出すため)、最小値が 0 で最大値が 1 になるように正規化されている。
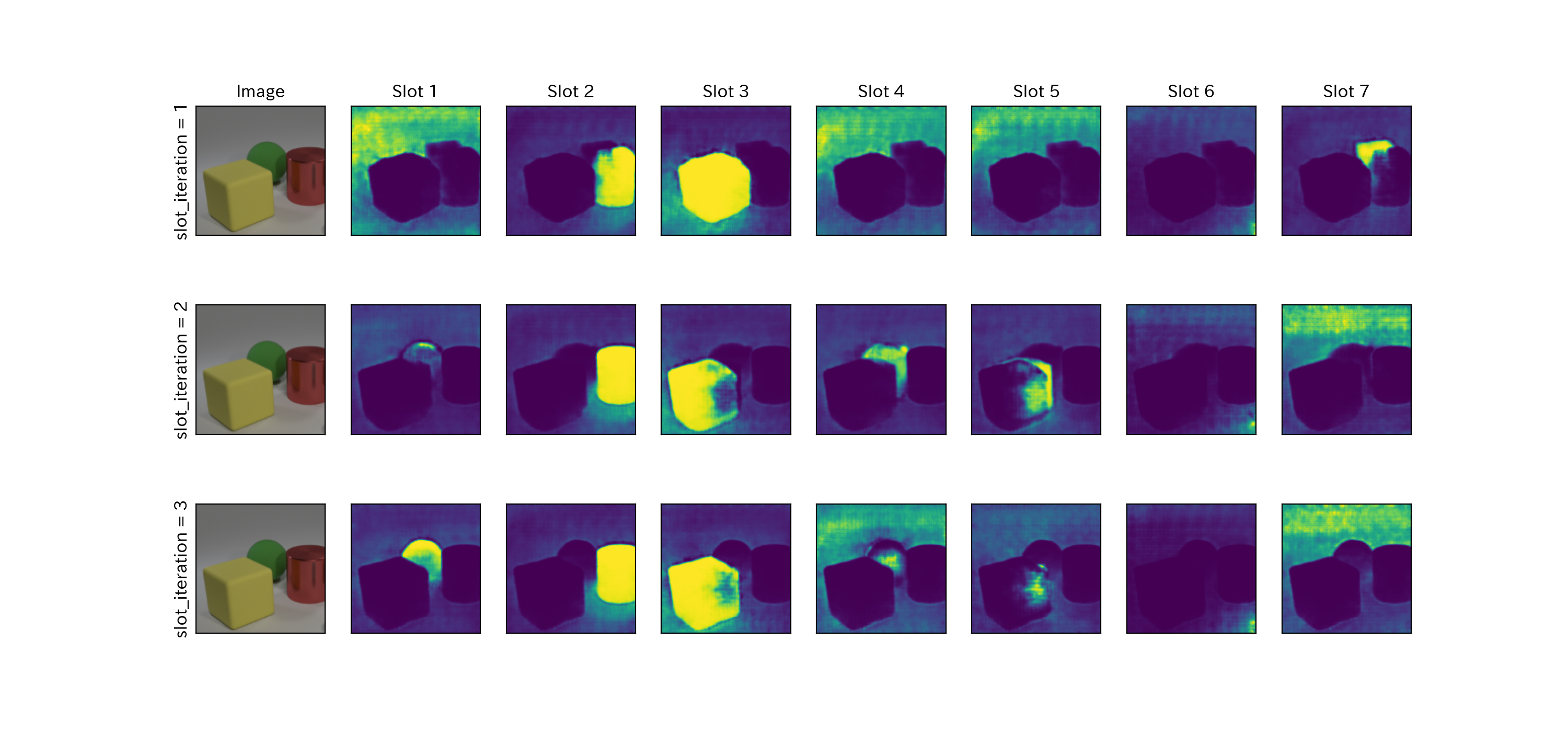
最後に、Queryを反復させることでslotは、入力された特徴マップの1部を解釈できるようになることを確認する。
下図の上から、再帰ニューラルネットの繰り返しごとに mask を行った図である。繰り返し数が1の場合は、各Slotにおいて同じ物体をmaskしているSlotがある。しかし、繰り返し数が3になると、Slot ごとに物体を検知し、物体がないところは空になっている。つまり、Queryを反復させることでSlotは、入力された特徴マップの1部を解釈できるようになっていると言える。
集合予測の結果
バッチサイズは16、Slot の数は7、再帰ニューラルネットの繰り返し数は3として学習させた。教師無し物体検知で学習させたエンコーダを転移させて学習を実行した。計算時間は約1日かかった。
以下の図を確認すると、誤差が順調に下がっていることが分かる。
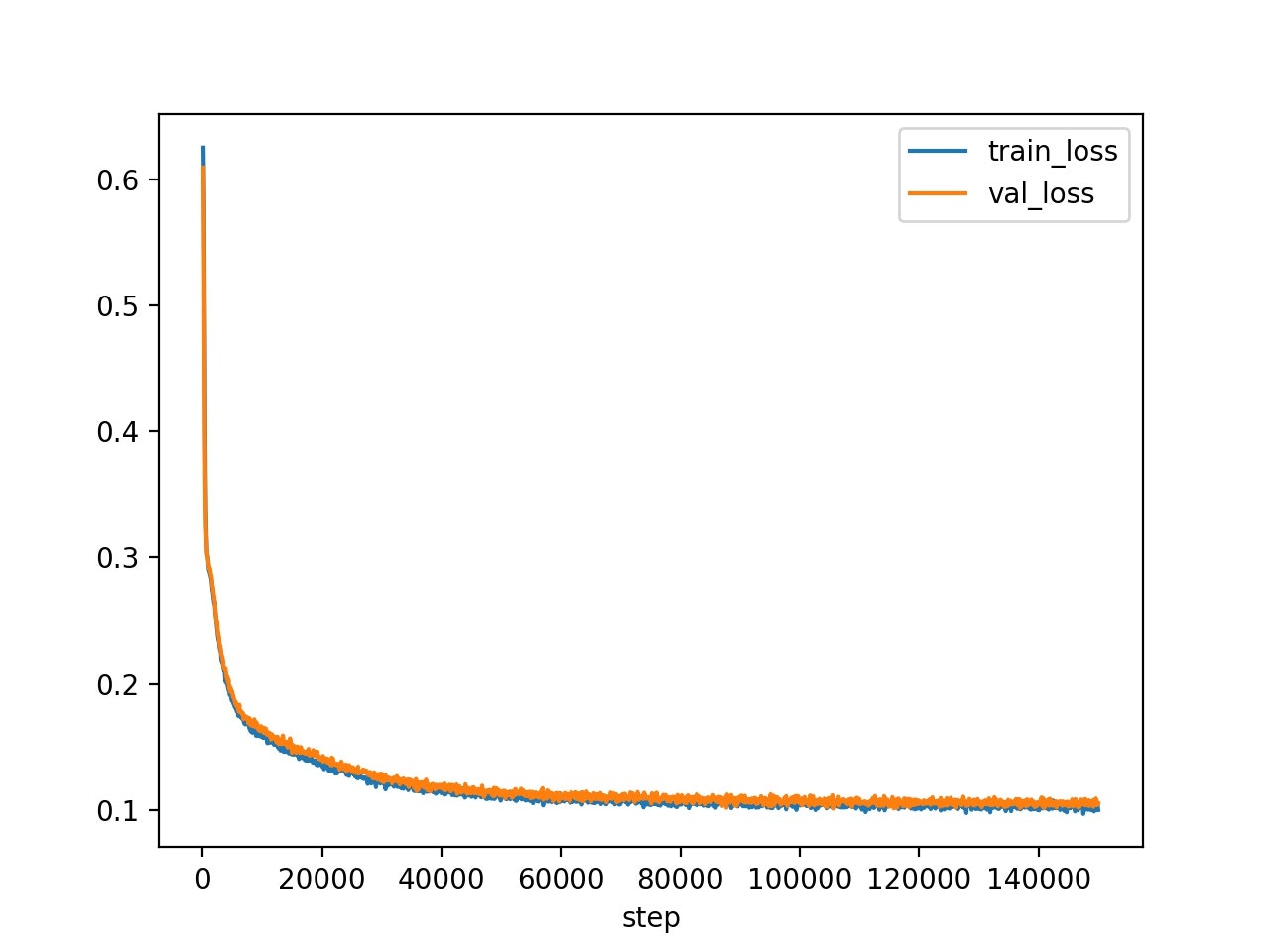
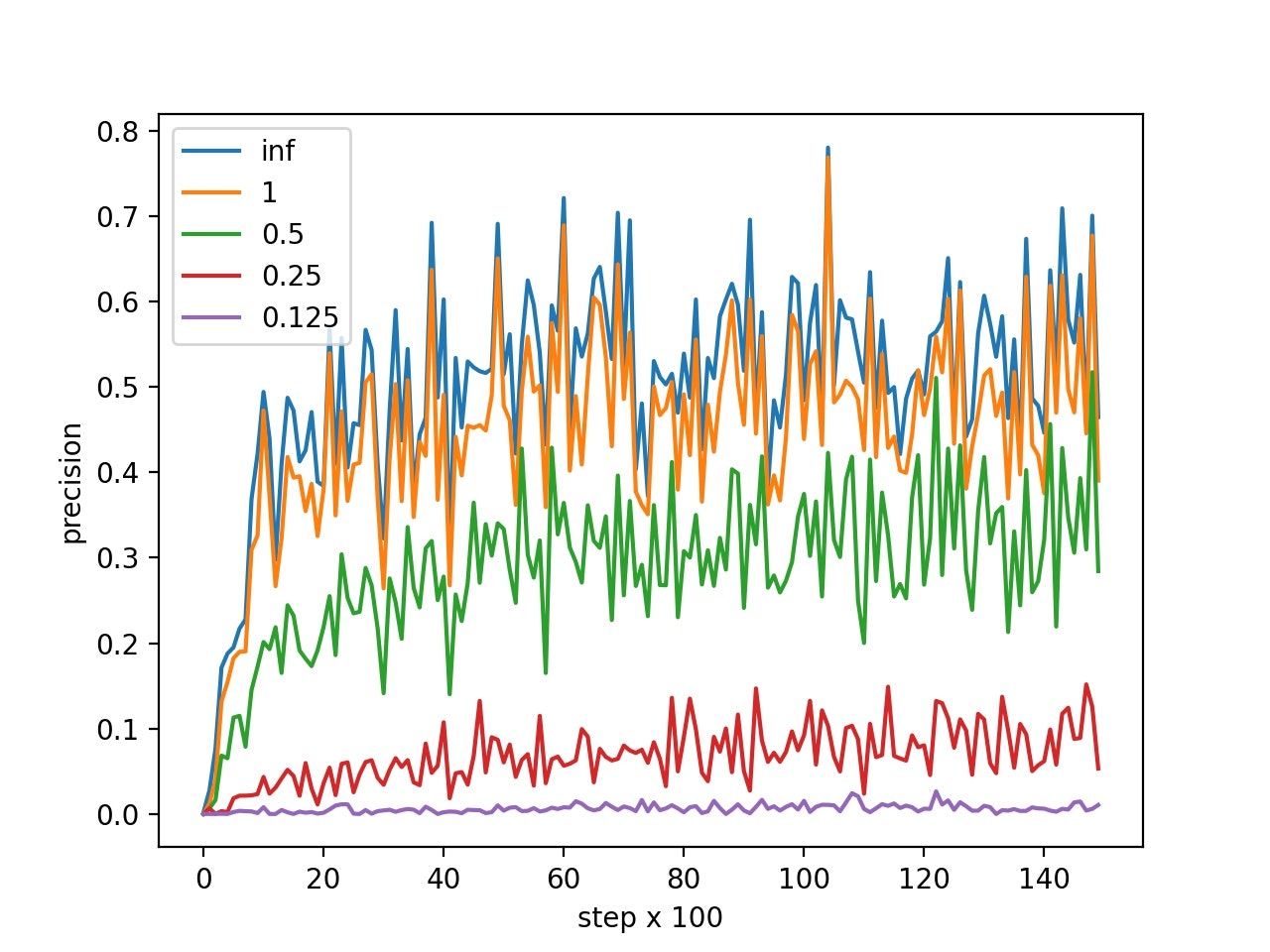
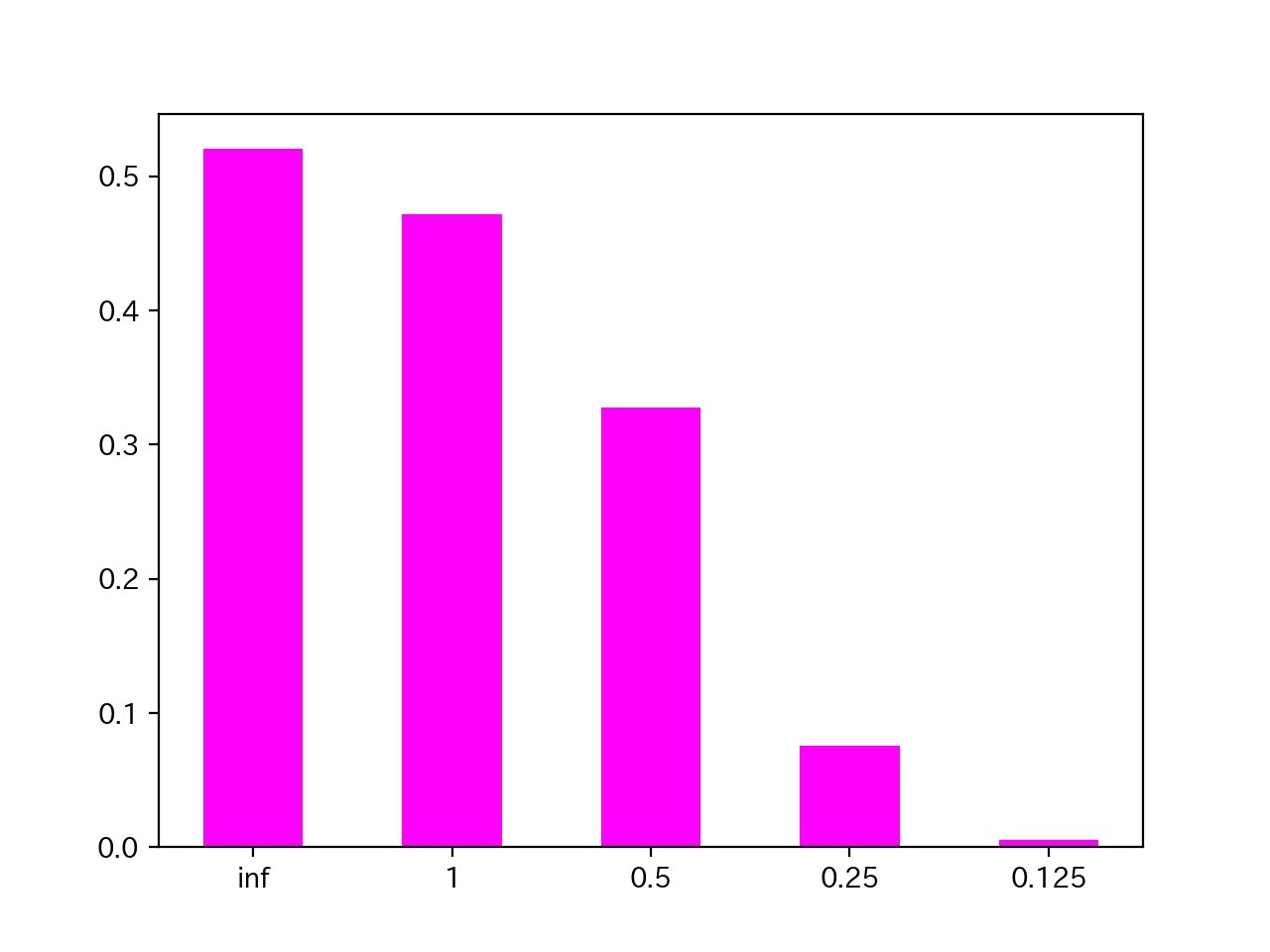
以下の図は、学習ステップごとの平均適合率をプロットしたものである。図の[inf,1,0.5,0.25,0.125]は、予測された物体と正解の物体との距離の閾値である。この閾値以内かつ、予測結果のサイズ・物性・形状・色が正解データと一致するなら正解とする。
論文と比べると値が低いので、もう少し学習が必要である。
最後に
今回の記事で使ったデータセットは、物体がはっきりしたデータセットである。物体がはっきりしていないような物体(物体とは言えない。。。地形など)を、検知できるか試す必要がある。