概要
土木の分野において、粒子法の研究が盛んにおこなわれています。例えば、離散要素法(DEM)、Smoothed Particle Hydrodynamics(SPH) 、Material Point Method(MPM)などがあります。
MPM は、メッシュ(グリッド)と粒子を組み合わせた計算方法であり、FEM(有限要素法)で生じるメッシュのねじれがなく、計算の途中でメッシュを使うので、SPH や MPS にくらべ計算が安定していると言われています。
前回の記事で、少し紹介しました。
https://qiita.com/fujitagodai4/items/ae6c1db61a0a6172a18f
MPMの欠点として、cell crossing error と呼ばれる、粒子がセルを横切った際に符号が入れ替わり数値振動が起こることが知られています。これは、グリッド上の計算で使う補間関数(形状関数)が原因です。(6 面体要素が使われる。)
この欠点を克服する方法として、補間関数を変更する方法、B-spline MPM (BSMPM) や generalized interpolation material point (GIMP) 、 convected particle domain interpolation (CPDI) などが知られています。
この記事では、Total Lagrangian Material Point Method (TLMPM) と呼ばれる方法について説明します。通常の MPM では、グリッド上で支配方程式を解くとき、そのグリッド上に配置されている現時点の粒子の情報を使い計算します。TLMPM では、グリッド上で支配方程式を解くとき、初期に配置されていた粒子の情報を使い計算するので、粒子がセルをまたぐことがなく、cell crossing error が起こらない利点があります。
以下の論文の内容を参考にしています。
MPM の簡単な復習
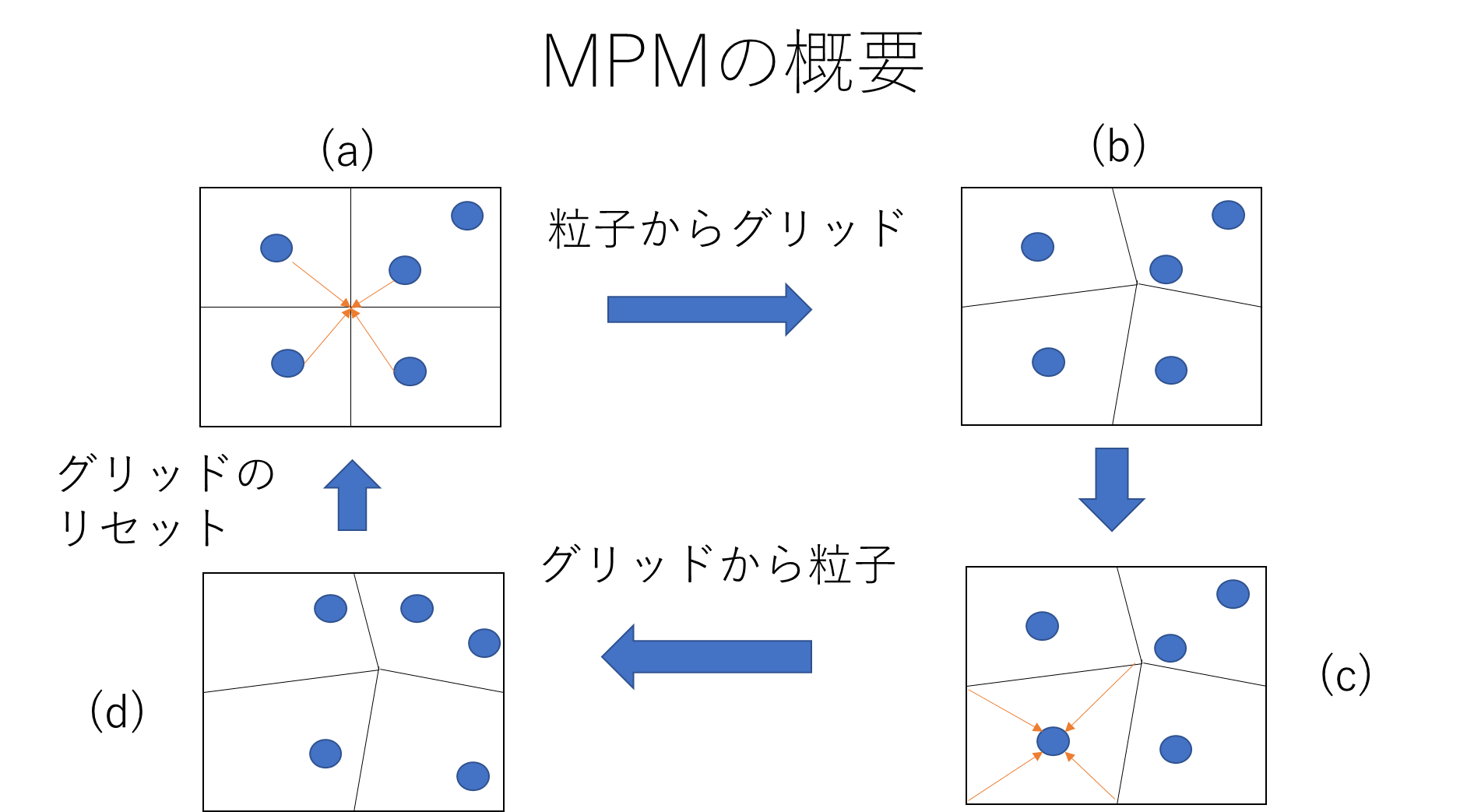
大まかな計算手順は以下の4手順である。
(a) 粒子の情報を使いグリッド点での物理量を計算する。
(b) 支配方程式を用いてグリッド点での物理量を更新する。
(c) グリッドの情報を用いて粒子の物理量を計算する。
(d) 粒子の物理量を更新し、グリッドをリセットする。
cell crossing error は、(c) から (d) の計算において、粒子が現時点にいるセルから違うセルに移動することで起きる。TLMPM では、計算で使う粒子はセルを移動しないので、cell crossing error の問題を避けることができる。
これについて説明すると、初期座標を $X$ とし、現座標を $x$ とする。通常の MPM では、グリッド上で使う粒子の情報は現配位 $x$ であるが、TLMPM では、グリッド上で使う粒子の情報は初期配位 $X$ であるので、粒子はセルを移動しない。
支配方程式
初期座標を $X$ とし変位を $u$ とすると、現座標 $x$ は
\begin{align}
x_i = X_i + u_i
\end{align}
と書ける。小文字の添え字は、空間座標を示す。Lagrangian 形式では、初期座標 $X$ の情報で応力を計算する。質量保存則と運動量保存則より支配方程式が導出され、
\begin{align}
\rho_0 &= J \rho \\
\\
\frac{\partial v_i}{\partial t} &= \frac{1}{\rho_0} \frac{\partial}{\partial X_j} P_{ij} +b_i \ , \
v_i = \frac{\partial u_i}{\partial t}
\end{align}
と書ける。$\rho_0,\rho$ は、初期密度・密度であり、$b$ は重力などの外力である。$J$ は変形勾配の行列式であり、変形勾配を用いて
\begin{align}
F_{ij} = \frac{\partial x_i}{\partial X_j} \\
\\
J = \mathrm{det}F
\end{align}
と書ける。$P$ は、(第一)Piola-Kirchhoff 応力テンソルである。この記事では、Neo-Hookean モデルを使用する。
\begin{align}
P_{ij} = \mu(F - F^{-T})_{ij} + \lambda \ln(J)(F^{-T})_{ij}
\end{align}
$\mu,\lambda$ は、ラメ定数である。
Particle to node mapping
グリッドノードの座標を大文字 $I,J,...$ の添え字を、粒子の添え字は $p$ を使う。グリッドノードにおける質量、速度(実際の計算では運動量を計算)、内・外力は、
\begin{align}
M_I &= \sum_{p} N_{I}(X_p)m_p \\
\\
V_I^{t^n} &= \frac{1}{M_I} \sum_{p} N_{I}(X_p)m_p v_p^{t^n}\\
\\
f_I^{int,t^n} &=-\sum_{p}V_{p}^0 P_p^{t^n} \nabla_0 N_{I}(X_p) \\
\\
f_I^{ext,t^n} &= \sum_{p} N_{I}(X_p)m_p b_p^{t^n} +M_Ib_I^{t^n} \\
\end{align}
と計算される。$N_I(X_p)$ は形状関数であり、$b_I^{t^n}$ はグリッドノードにおける外力である($P_{ij}n_j$に相当する表面力)。$V_{p}^0 $ は粒子の初期体積であり、$\nabla_0 $ は初期座標 $X$ における微分を表す。添え字が煩雑になるので、空間添え字は省いた。上付き添え字$t^{n}$ は、$n$ 時間ステップにおける物理量を示す。
通常の MPM では、現座標を使い形状関数の値 $N_I(x_p)$ が 計算される。また、グリッドノードの質量は、粒子がセルを移動するので、各時間ステップ $t^{n}$ において異なる。TLMPM では、初期座標を使い計算を行うので、グリッドノードにおいても質量は保存される。よって、最初のステップのみ計算すればよい。
Update nodal momenta and fix Dirichet nodes
グリッドノードにおける速度の更新(実際の計算では運動量を更新)を行う。MUSL(Modified Update Stress Last )を使うので、一時的な速度を
\begin{align}
\tilde{V}_I^{t^{n+1}} = V_I^{t^{n}} + \frac{\Delta t^{t^n}}{M_I}\left(f_I^{ext,t^n}+f_I^{int,t^n} \right)
\end{align}
と更新する。
Dirichet 境界条件においては、
\begin{align}
\tilde{V}_I^{t^{n+1}} = 0
\end{align}
とする。
Update particle position and velocities
一時的な速度を用いて、粒子の速度・加速度・位置の更新を行う。
\begin{align}
\tilde{v}_p^{t^{n+1}} &= \sum_I N_{I}(X_p)\tilde{V}_I^{t^{n+1}}\\
\\
\tilde{a}_p^{t^{n+1}} &= \sum_I N_{I}(X_p)\frac{\tilde{V}_I^{t^{n+1}}-{V}_I^{t^{n}} }{\Delta t^{t^n}} \\
\\
x_p^{t^{n+1}} &= x_p^{t^{n}} + \Delta t^{t^n}\tilde{v}_p^{t^{n+1}}
\end{align}
粒子の最終的な速度は、Pure particle in cell (PIC) と Fluid implicit particle method (FLIP) を組み合わせる。
PICは、速度を
\begin{align}
v_p^{t^{n+1}} = \tilde{v}_p^{t^{n+1}}
\end{align}
と更新する。PICは、安定性あるが散逸性が高い。FLIPは、速度を
\begin{align}
v_p^{t^{n+1}} = v_p^{t^{n}} + \Delta t^{t^n} \tilde{a}_p^{t^{n+1}}
\end{align}
と更新する。PICは、安定性を犠牲にして散逸性を低くする。
粒子の最終的な速度は、パラメータ $\beta$ として、
\begin{align}
v_p^{t^{n+1}} = (1-\beta)\tilde{v}_p^{t^{n+1}} +\beta(v_p^{t^{n}} + \Delta t^{t^n} \tilde{a}_p^{t^{n+1}} )
\end{align}
とする。パラメータは、$\beta = 0.99$ が使われる。
Update particle Deofrmation gradient
最後にMUSLを使い、再計算されたグリッドノードにおける速度から、変形勾配の更新を行う。
MUSLによって、グリッドノードにおける速度を更新する。
\begin{align}
V_I^{t^{n+1}} &= \frac{1}{M_I} \sum_{p} N_{I}(X_p)m_p v_p^{t^{n+1}}
\end{align}
変形勾配の時間微分は、
\begin{align}
\dot{F} = \frac{\partial }{\partial X}\frac{\partial u}{\partial t} = \frac{\partial v}{\partial X}
\end{align}
なので、
\begin{align}
\dot{F}_p^{t^{n+1}} = \sum_I V_I^{t^{n+1}}\otimes \nabla_0 N_{I}(X_p)
\end{align}
と計算される。空間添え字を陽に書くと、
\begin{align}
(\dot{F}_{p}^{t^{n+1}})_{ij} = \sum_I (V_I^{t^{n+1}})_i \frac{\partial}{\partial X_j} N_{I}(X_p)
\end{align}
となる。
変形勾配の更新は、
\begin{align}
F_p^{t^{n+1}} = F_p^{t^{n}} + \Delta t^{t^{n}} \dot{F}_p^{t^{n+1}}
\end{align}
と更新される。その結果を用いてPiola-Kirchhoff 応力テンソルを計算する。
\begin{align}
P_{p}^{t^{n+1}} = \mu\left(F_p^{t^{n+1}} - (F_p^{t^{n+1}})^{-T} \right) + \lambda \ln(\mathrm{det} F_p^{t^{n+1}}) (F_p^{t^{n+1}})^{-T}
\end{align}
また、密度の更新は、初期密度 $\rho_p^{0}$ を使い
\begin{align}
\rho_p^{t^{n+1}} = \frac{\rho_p^{0}}{\mathrm{det} F_p^{t^{n+1}}}
\end{align}
と更新される。
時間の刻み幅は、各ステップごとに
\begin{align}
\Delta t \leq \frac{h}{c}
\end{align}
を満たすように決める。$h$ はセルのサイズであり、$c$ は
\begin{align}
c = \sqrt{\frac{K+4\mu/3}{\rho} }
\end{align}
と計算される。$K$ は体積弾性率である。
Vertical bar in gravity field
1m × 1m × 1m の棒を天井に吊り下げ、重力を$1000m/s^2$(本来の近しい値は$9.8m/s^2$)をかけるシミュレーションを行った。形状関数は、6 面体要素を使った。
ヤング率・ポアソン比・初期密度は
\begin{align}
E &= 1.0\times 10^{6} \ \ \mbox{Pa} \\
\nu &= 0.3 \\
\rho_0 &= 1050 \ \ \mbox{kg}/m^3
\end{align}
と設定し、シミュレーション時間は $0.25$秒とした。
セルサイズは $1/30$ $m$ とし、1つのセルに $27$ 個の粒子が入るように設定した。
シミュレーション結果は、以下の通りである。
以下の図は、下端の1つの粒子の変位を時間ごとにプロットしたものである。
厳密解と比較はしていないが、引用した論文と似たような結果である。
(引用した論文では、他2つの補間関数でシミュレーションを行っている。TLMPMの特性により、そこまで大きな差がなかったと考える。)
最後に
最終的には、塑性変形・土水連成計算など行いたい。