高校数学で解けるAtCoderのC問題まとめ

この記事は湧源クラブ Advent Calendar 2019 の記事（16日目）です。
**AtCoder Beginner Contestの解法に関するネタバレが含まれます。**読む際は注意してください。

##数学の力だけで水色になれる
夏季27回参加のfujioka_mathです。
生活に面白みを加えたくて、まわりの人々がやっていたAtCoderを始めてみました。

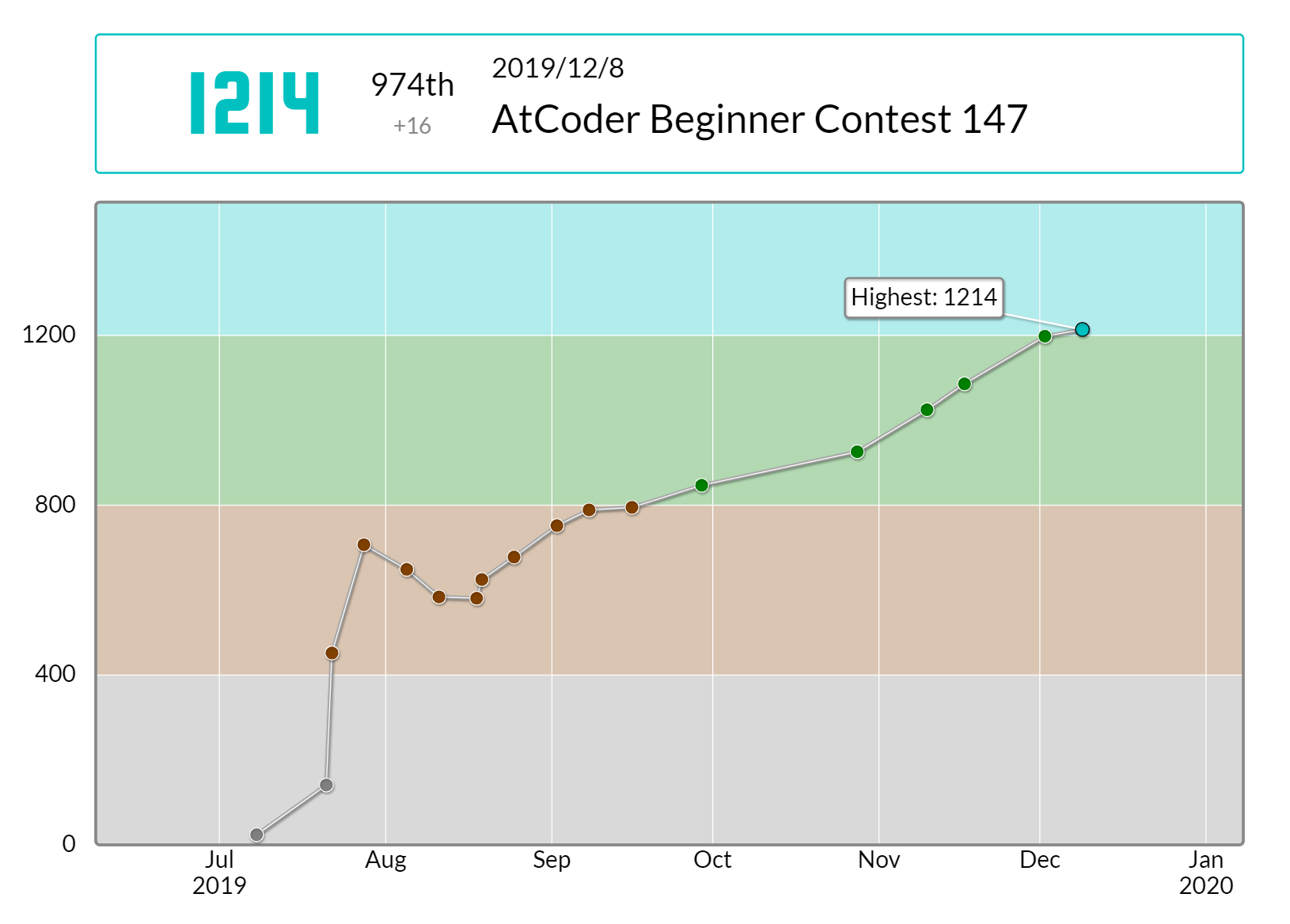
約5か月で水色になれました。（画像は12/16時点。アカウントはfujioka_1115です）

水色になったわけですが、正直アルゴリズムには全然詳しくありません。数学の力で単純に解ける問題を素早く解いて、ABCのE問題を一度も解くことなくギリギリ到達した感じです。

##数学力でゴリ押せ
ABCのC問題やD問題には、アルゴリズムに明るくなくても解ける問題がいくつかあります。
たとえばこういうものです。

問題を表示

###ABC144 D - [Water Bottle](https://atcoder.jp/contests/abc144/tasks/abc144_d) **【問題の概要】** 底面が$a\times a$、高さが$b$の直方体の容器に水が$x$入っている。 水を溢れさせずに容器を（正方形の1辺を軸として）傾けるとき、最大で何度傾けられるか？

解答例を表示

これは完全に数学の問題。tanの逆関数arctanを使う。 $x$と$\frac{a^2b}2$の大小で場合分けすると楽。 arctanは大学内容では？という疑問が出ると思いますが、ここではarctanの性質は一切使っておらず、逆関数自体は数学IIIの内容なので高校数学とします。

import math
a,b,x=[int(s) for s in input().split()]
if x>a*a*b/2:
  h=2*(a*a*b-x)/(a*a)
  print(math.degrees(math.atan(h/a)))
else:
  k=2*x/(a*b)
  print(math.degrees(math.atan(b/k)))

これはD問題でありながらアルゴリズムを使いません。
今回はこのような数学の力があれば楽に解ける問題を紹介するので、プログラミング初心者のクラブ員もどんどん挑戦してみてください。

##対象とする問題

• AtCoder Beginner Contestの第101回以降のC問題
• AtCoder Problemsで表示されるDifficultyが400（茶）以上
• 高校数学だけで解けるもの
• 文字列の操作、累積和などが出てくる問題は対象外

##使用言語、注意点

• Pythonを使用。
• 配列の扱いやif文、for文などの知識は仮定します。（これは簡単なのですぐ身に付きますよ！）
• 僕は以下の解答をすべて初見で思いついたわけではなく、解説や他人の解答から学んだ部分も多くあります。
• 解答例よりもっと良い解答がたくさんあると思うので、参考程度にとどめてください。

##C問題

###ABC101 C - Minimization

考え方

問題文の「$A_1, A_2, \dots , A_n$は$1, 2, \dots , N$を並び替えたもの」というところさえ見逃さなければ、長さ$K$の区間がいくつあれば全体を覆えるか？という問題であることに気づく。

解答例

N,K=[int(s) for s in input().split()]
print((N+K-3)//(K-1))

必要な区間の個数は$\left\lceil\dfrac{N-1}{K-1}\right\rceil$です。
ここでは$\left\lceil\dfrac nm\right\rceil=\left\lfloor\dfrac {n+m-1} n\right\rfloor$を用いて、天井関数を呼び出さずに書いています。
（この式もABCの解説で知りました。）

###ABC105 C - Base -2 Number

考え方

数学Ｉで習う$n$進数の発展であり、特に悩むことはない。 割り算した余りを順番に出力すればよい。

解答例

N=int(input())
ls=[]
while True:
  ls.append(N%2)
  N=-(N//2)
  if N==0:
    break
print(*reversed(ls),sep="")

この問題で一番苦労したのは、[1,1,0,1]のような数字のリストを1011のように逆順に、しかも繋げて出力するところ。
リストをつなげて出力するのはprint(*ls,sep="")で簡単にできることを以前おしえてもらいました。
それから、細かいところですが$N=0$のときに一敗しています。

###ABC108 C - Triangular Relationship

考え方

数学Ａの「整数」分野の考え方を使う。 $K$が奇数のとき、$a+b,b+c,c+a$が全て$K$の倍数であることは$a,b,c$がすべて$K$の倍数であることと同値。 $K$が偶数のときは、「$a,b,c$がすべて$K$の倍数、または$a,b,c$がすべて$\frac K2$の倍数かつ$K$の倍数でない」と同値。 よってそれぞれの場合について倍数の個数を調べて3乗して、足せばよい。

解答例

N,K=[int(s) for s in input().split()]
if K%2==1:
  print((N//K)**3)
else:
  print((N//K)**3+((N//(K//2)-N//K)**3))

###ABC109 C - Skip

考え方

$x_1-X,x_2-X,\dots,x_n-X$の最大公約数を出力すればよい。 Pythonには最大公約数を求める関数gcdがあるが、AtCoderではPythonのバージョンが3.4であるためmathモジュールでなくfractionsモジュールでgcdを使う。これは負の値を返すこともあるので注意。

解答例

import fractions
N,X=[int(s) for s in input().split()]
ls=[int(s)-X for s in input().split()]
a=0
for e in ls:
  a=fractions.gcd(a,e)
print(abs(a))

###ABC116 C - Grand Garden

考え方

自分は初見でいい方法がわからなかったが…

隣り合う花と両端の地面の高さの差（の絶対値）の総和が、必要な水やりの回数の2倍になっていることがわかる。

より単純に、緑の部分だけ足せば答えがそのまま得られる。これを出力すればよい。

解答例

N=int(input())
ls=[int(s) for s in input().split()]
ls.append(0)
a=0
for i in range(N):
  a+=max([0,ls[i]-ls[i+1]])
print(a)

###ABC117 C - Streamline

考え方

どちらかといえば、配列の基本的な操作ができるかどうかを聞いている問題。 $X_1 階差数列$Y_n=X_{n+1}-X_n$を考え $Y_1,\dots,Y_n$の大きいもの上位$N-1$個を取り除き 残ったものの総和を出力すればよい。

階差数列なので一応数学Ｂか。

解答例

N,M=[int(s) for s in input().split()]
if N>=M:
  print(0)
else:
  ls=[int(s) for s in input().split()]
  ls.sort()
  d=[ls[i+1]-ls[i] for i in range(M-1)]
  d.sort()
  print(sum(d[:M-N]))

$N\ge M$のときには答えは自動的に0になる。
最後の行のd[:M-N]は、配列dを途中で（M-Nの手前までで）切り取ったもの。

###ABC118 C - Monsters Battle Royale

考え方

$A_1, A_2, \dots , A_n$の最大公約数を出力するのみ。

解答例

import fractions
N=int(input())
ls=[int(s) for s in input().split()]
a=0
for e in ls:
  a=fractions.gcd(a,e)
print(a)

###ABC123 C - Five Transportations

考え方

5つの輸送手段のうち最も遅いものがカギになる。 化学でいうところの律速段階。

最も遅い輸送手段でN人を運ぶのにかかる時間を求めれば、その時間＋4分が答え。

解答例

import math
N = int(input())
A = int(input())
B = int(input())
C = int(input())
D = int(input())
E = int(input())
X = min([A,B,C,D,E])
t=math.ceil(N/X)
print(t+4)

あるいは$\left\lceil\dfrac NX\right\rceil=\left\lfloor\dfrac {N+X-1} X\right\rfloor$を用いるなどして

N = int(input())
ls = [int(input()) for i in range(5)]
X = min(ls)
print((N+X-1)//X+4)

###ABC126 C - Dice and Coin

考え方

数学Ａの問題。特記事項無し。 logを使ってもよいが、使わずに二重のforループを回しても間に合う。

解答例

import math
N,K=[int(s) for s in input().split()]
a=0
for i in range(N):
  a+=2**(-max([0,math.ceil(math.log2(K/(i+1)))]))
print(a/N)

あるいはfor文とwhile文を組み合わせて（二重ループ）、こう書くこともできる。
僕の場合、こういう「頭のよくない」方法を用いたほうが単純ミスは少ない。

N,K=[int(s) for s in input().split()]
a=0
for i in range(N):
  x=i+1
  n=0
  while x<K:
    n+=1
    x*=2
  a+=2**(-n)
print(a/N)

###ABC129 C - Typical Stairs

考え方

高校数学の有名な問題。漸化式を用いるもの。 $n$段目まで上がる方法の数を$b_n$としたとき、

b_{n}=  \begin{cases}
     b_{n-1}+b_{n-2} \quad (n\text{段目が壊れていない})\\
     0\qquad (n\text{段目が壊れている})
  \end{cases}

が$n\ge2$に対して成り立つ。
この再帰を実装する方法は、実は初心者には難しいのでこの記事で扱うかどうか悩んだが、あまりにも高校数学なので扱ってしまった。

解答例

「メモ化再帰」と呼ばれるものを使った。

MOD=10**9+7
N,M=[int(s) for s in input().split()]
ls=[1 for _ in range(N+1)]
for i in range(M):
  ls[int(input())]=0
for n in range(2,N+1):
  if ls[n]!=0:
    ls[n]=(ls[n-1]+ls[n-2])%MOD
print(ls[N])

###ABC130 C - Rectangle Cutting

考え方

特に何も言うことはない。2等分は常に可能で、点$(x,y)$が長方形の対角線の交点であれば複数通りの切り方が可能。 場合によっては中学校の「線対称、点対称」の授業で扱うはず。

解答例

W,H,x,y = [int(s) for s in input().split()]
if 2*x==W and 2*y==H :
  print(W*H/2,1)
else:
  print(W*H/2,0)

###ABC131 C - Anti-Division

考え方

完全に高校数学。数学Ａの「集合と論理」分野。 「全体の個数」－「$C$の倍数の個数」－「$D$の倍数の個数」＋「$C,D$の公倍数の個数」を出力すればよい。

また、$A$以上$B$以下である$x$の倍数の個数は、「$B$以下の$x$の倍数の個数」－「$A-1$以下の$x$の倍数の個数」で求められる。

ちなみにfractionsモジュールには最小公倍数を求める関数lcmがない。
よって$C\times D \div gcd(C,D)$で最小公倍数を求めてみた。これは数学Ａの「整数」分野の内容。

解答例

import fractions
A,B,C,D = [int(s) for s in input().split()]
L=C*D//fractions.gcd(C,D)
print(B-(A-1)
      -(B//C)+((A-1)//C)
      -(B//D)+((A-1)//D)
      +(B//L)-((A-1)//L))

##もっと簡単なC問題もある
これまでのものはAtCoder Problemsで表示されるDifficulty、つまり正解者のレートの中央値が400(茶)以上の問題であり、実際にはもっと楽に解けるもの（灰色相当のもの）も多いです。

##結局アルゴリズムを学ぶことになる

###D問題以上は
D問題以上になると「高校数学のこの部分！」という問題は少なくなってしまいます。

しかも、数学の力で単純化したとしても実装にはアルゴリズムの知識がなお必要となる（実行時間の制限に引っかかる）ことが多いので、最初に紹介した144Dや139Dのような「簡単」な問題はほとんどないのが現実です。

###アルゴリズムの勉強もたのしい
なので、やっぱりアルゴリズムの勉強もしましょう。

解けない問題の解説を見るととても鮮やかな解法や興味深いアルゴリズムが載っていて、楽しいです（ただし読んだ直後は自分の無力さに落ち込みます）。
これを楽しめれば競プロを楽しめるのではないでしょうか。