Q-Learningを用いて、迷路の探索をCで実装します。
強化学習とは
一連の行動の最後に評価を与え、この評価にしたがって学習をすすめる手法です。
最後の評価値を用いて一連の動作の中の、一つ一つの個別の行動について知識を学習していきます。
Q学習とは
Q値というのは、将来を見据えたうえでその選択がどのくらい良いものなのかの基準となる値です。
報酬を得た場合報酬と繋がる行動のQ値を増加させていきます。
また、報酬を得なかった場合は、次の状態のうち最大のQ値を利用して更新します。
学習の目標はこのようにして適切なQ値を獲得することになります。
Q値更新の数式は以下のようになります。
Q(St,At)=Q(St,At)+α(r+γmax(St+1,At+1)-Q(St,At))
r :報酬(得られなかったら0)
α:学習係数(0.1程度) →学習の速度を調整します
γ:割引率 →未来(ここではひとつ先)のQ値をどれほど重視するか決める値です
つまり、「もし報酬が得られたら報酬に比例した値をQ値に加える。
次の状態で選択できる行動に対するQ値のうち最大値に比例した値をQ値に加える。」
ということをしているのです。
学習の手順まとめ
1.すべてのQ値を乱数で初期化
2.学習が十分進むまで以下を繰り返す
(2.1)動作の初期状態に戻る
(2.2)選択可能な行動からQ値に基づいて次の行動を決定する
(2.3)行動後、Q値を更新
(2.4)ある条件(目標状態or一定時間経過)を満たしたら2.1.に戻る
(2.5)2.2.に戻る
コードの概要
迷路抜けをします。なるべく多くの報酬がもらえるような行動を学習していきます。
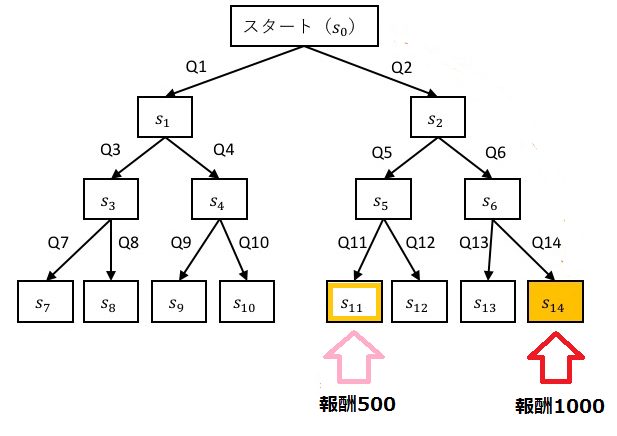
状態s14,s11にたどり着くとそれぞれ1000,500の報酬がもらえます。
報酬が大きくなるような経路を探すのが目標です。
学習手順(2.4)の条件については、「GENMAXで定義した回数だけ学習したら」とします。
コード解説1〜Q値更新について
報酬が生じる場合(最下段の状態11か14)は
qv=qvalue[s]+ALPHA*(REWARD-qvalue[s]);
生じない場合(最下段以外)は
qv=qvalue[s]+ALPHA*(GAMMA*qmax-qvalue[s]);
となります。
int updateq(int s,int qvalue[NODENO]){
int qv; //更新されるQ値
int qmax; //Q値の最大値
if(s>6){ //最下段
if(s==14)qv=qvalue[s]+ALPHA*(REWARD1-qvalue[s]); //報酬の付与
else if(s==11)qv=qvalue[s]+ALPHA*(REWARD2-qvalue[s]);
else qv=qvalue[s];
}
else{ //最下段以外
if((qvalue[2*s+1])>(qvalue[2*s+2]))qmax=qvalue[2*s+1];
else qmax=qvalue[2*s+2];
qv=qvalue[s]+ALPHA*(GAMMA*qmax-qvalue[s]);
}
return qv;
}
コード解説2〜ε-greedyによる行動選択について
ε-greedy法とは、乱数を用いてある割合でランダムに行動を選択する手法です。
0~1の乱数を生成して、あらかじめ定義したEPSILONよりも大きければQ値の大きいものに対応する行動を選択します。EPSILON以下であったらランダムに行動を選択します。
これにより、Q値の初期値と運に影響されずに、適切な探索ができるようになります。
int selecta(int olds,int qvalue[NODENO]){
int s;
if(rand1()<EPSILON){ //ランダムに行動
if(rand01()==0)s=2*olds+1;
else s=2*olds+2;
}
else{ //Q値最大値を選択
if((qvalue[2*olds+1])>(qvalue[2*olds+2]))s=2*olds+1;
else s=2*olds+2;
}
return s;
}
結果
 s1~s14の重みづけ(選ばれやすさ)がこのように表示されます。(最後の数十回のみ表示しています)
s2,s6,s14が大きくなっていることがわかります。
s1~s14の重みづけ(選ばれやすさ)がこのように表示されます。(最後の数十回のみ表示しています)
s2,s6,s14が大きくなっていることがわかります。
コード全文
#include<stdio.h>
#include<stdlib.h>
#define _CRT_SECURE_NO_WARNINGS
#define NODENO 15 //Q値のノード数
#define GENMAX 1000 //学習の繰り返し回数
#define ALPHA 0.1 //学習係数
#define GAMMA 0.9 //割引率
#define EPSILON 0.3 //行動選択のランダム性を決定(閾値)
#define REWARD1 1000 //報酬
#define REWARD2 500
#define DEPTH 3 //道のりの深さ
#define SEED 3277
int rand100(); //0~100の乱数
int rand01(); //0or1の乱数
double rand1(); //0~1の乱数
void printqvalue(int qvalue[NODENO]); //Q値出力
int selecta(int s,int qvalue[NODENO]); //行動選択
int updateq(int s,int qvalue[NODENO]); //Q値更新
/***********************************/
int main(){
int qvalue[NODENO]; //Q値
int s; //状態
int t; //時間
srand(SEED);
//Q値の初期化
for(int i=0;i<NODENO;++i)qvalue[i]=rand100();
printqvalue(qvalue);
//学習の本体
for(int i=0;i<GENMAX;++i){
s=0; //行動の初期化
for(t=0;t<DEPTH;++t){
s=selecta(s,qvalue); //行動選択
qvalue[s]=updateq(s,qvalue); //Q値の更新
}
if(i%20==0){
for(int j=1;j<NODENO;++j)printf("s=%d\t",j);
printf("\n");
}
printqvalue(qvalue);
}
return 0;
}
/*******************************************/
/*Q値を更新する*/
int updateq(int s,int qvalue[NODENO]){
int qv; //更新されるQ値
int qmax; //Q値の最大値
if(s>6){ //最下段
if(s==14)qv=qvalue[s]+ALPHA*(REWARD1-qvalue[s]); //報酬の付与
else if(s==11)qv=qvalue[s]+ALPHA*(REWARD2-qvalue[s]);
else qv=qvalue[s];
}
else{ //最下段以外
if((qvalue[2*s+1])>(qvalue[2*s+2]))qmax=qvalue[2*s+1];
else qmax=qvalue[2*s+2];
qv=qvalue[s]+ALPHA*(GAMMA*qmax-qvalue[s]);
}
return qv;
}
/*行動を選択(ε-greedy)*/
int selecta(int olds,int qvalue[NODENO]){
int s;
if(rand1()<EPSILON){ //ランダムに行動
if(rand01()==0)s=2*olds+1;
else s=2*olds+2;
}
else{ //Q値最大値を選択
if((qvalue[2*olds+1])>(qvalue[2*olds+2]))s=2*olds+1;
else s=2*olds+2;
}
return s;
}
/*Q値表示*/
void printqvalue(int qvalue[NODENO]){
for(int i=1;i<NODENO;++i)printf("%d\t",qvalue[i]);
printf("\n");
}
/*乱数*/
double rand1(){ //0~1
return (double)rand()/RAND_MAX;
}
int rand01(){ //0or1
int rnd;
while((rnd=rand())==RAND_MAX);
return (int)((double)rnd/RAND_MAX*2);
}
int rand100(){ //0~100
int rnd;
while((rnd=rand())==RAND_MAX);
return (int)((double)rnd/RAND_MAX*101);
}