今回は ナイーブベイズ分類器について
ガウシアン、ベルヌーイ分布、多項分布の事象モデルについて scikit-learn を使って試してみます。
ナイーブベイズ分類器
ナイーブベイズ分類器とは
- 高速な分類アルゴリズム
- 高次元のデータセットに適している
- ナイーブベイズ=単純ベイズ
- 迷惑メールの分類などに使われている
- ベイズの定理が使われている
ベイズの定理
ベイズの定理は以下となり、確率および条件付き確率に関して、P(X) > 0 のとき次が成り立つ
P(Y|X) = \frac{P(Y)P(X|Y)}{P(X)}\\
この時、P(Y|X) は事後確率、P(Y) は事前確率、P(X|Y) は尤度と呼ばれる。
また、X については定数と考えることが出来るため、比例関係で表すと以下のようになり、
事後確率は事前確率と尤度の積に比例する。
{P(Y|X)\propto P(Y)P(X|Y)}
メモ:
P(Y|X) は X を与えたときの Y の条件付き確率を示す。
※読み方:X given Y
https://atarimae.biz/archives/15536
単純ベイズ確率モデル
上記の比例式を元に確率モデルを作成する。
確率モデル
入力変数を x(N個の特徴)、クラスを C(K個) とすると以下のように表せる。
\begin{eqnarray}
P(C_k | x_1,x_2,...,x_N) &\propto& P(C_k, x_1,x_2,...,x_N)\\
&=& P(C_k)P(x_1, x_2,...,x_n|C_k)\\
&=& P(C_k)\prod_{n=1}^{N} P(x_n|C_k)
\end{eqnarray}
確率モデルから分類器を構築
分類器は以下の式で表すことができ、一番確率の高いクラスへ分類する。
\hat{y} = argmax_{k\in{\{1,...,K\}}}
\biggl[ P(C_k)\prod_{n=1}^{N} P(x_n|C_k) \biggr]\\
\\
\hat{y} \in{ \{1,...,K \} }
尤度
分類器を使う上で、確率分布毎に固有パラメータが必要となります。
固有パラメータの最適な値は、以下の尤度関数を最大化する問題を解く事によって求めます。
尤度関数
尤度関数をL(x, C)とすると、以下のように書くことが出来ます。
L(x, C) = \prod_{k=1}^{K}
\biggl[
P(C_k)\prod_{i=1}^{n} P(x_i|C_k)
\biggr]
計算の簡略化、及び、アンダーフロー防止のため対数を取ります。
確率の積を和に変換する事が出来るため、
値が小さくなりすぎる事によるアンダーフロー発生を防止する事が出来ます。
\log L(x, C) = \sum_{k=1}^{K}
\biggl[
\log P(C_k) + \sum_{n=1}^{N} \log P(x_i|C_k)
\biggr]
あとは、それぞれの事象モデルごとに尤度関数を最大化する式(微分した結果=0)を求め、
学習を繰り返す事によって、固有パラメータの最適な値を求めます。
以下、各事象モデルを scikit-learn で試して行きます。
ガウスモデル (Gaussian naive Bayes)
- 特徴ベクトルにガウス分布(正規分布)を仮定する場合に使われる。
- 連続データを扱う場合に使われる。
- 固有パラメータは μ:平均 と σ^2:分散
事象モデル(Event Model)
P(x = v|C_k) = \frac{1}{\sqrt{2\pi\sigma_k^2}}e^{-\frac{(v-\mu_k)^2}{2\sigma_k^2}}
\\
\mu : 平均
\\
\sigma^2 : 分散
クラス
sklearn.naive_bayes.GaussianNB クラスを使用します。
サンプルコード
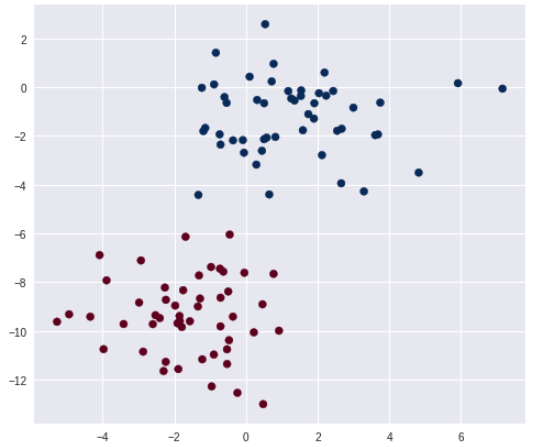
正規分布に従った乱数を発生させます。
データ件数は 100件、クラス数2、標準偏差は 1.5 になります。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=100, n_features=2, random_state=2, centers=2, cluster_std=1.5)
print("X[:5] =", X[:5])
print("y[:5] =", y[:5])
plt.figure(figsize=(8, 7))
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
先頭5件のデータは以下の通りです。
X[:5] = [[ 0.92141506 -9.98499137]
[-5.26927614 -9.6186543 ]
[-0.45292089 -6.04316334]
[-0.0856312 -2.16867404]
[ 1.53194956 -0.36022153]]
y[:5] = [0 0 0 1 1]
データをプロットします。
モデルの作成と予測
GaussianNB クラスを使い、モデルの作成と学習を行い、
データ先頭5件をそのまま予測します。
model = GaussianNB()
model.fit(X, y)
model.predict(X[:5])
array([0, 0, 0, 1, 1])
分類境界線可視化
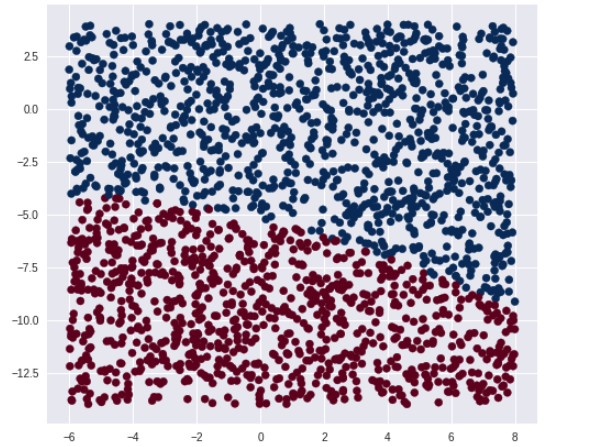
テストデータとして、ランダムに2000件発生させ、
予測結果を全てプロットしてみます。
rnd = np.random.RandomState(0)
X_test = [-6, -14] + [14, 18] * rnd.rand(2000, 2)
# 予測
Y_pred = model.predict(X_test)
# 境界線
plt.figure(figsize=(8, 7))
plt.scatter(X_test[:, 0], X_test[:, 1], c=Y_pred, s=50, cmap='RdBu')
各クラスの確率を可視化
predict_proba() を使うと、各クラスの確率が取得出来ます。
# 各クラスの確率
Y_prob = model.predict_proba(X_test)
print(Y_prob[20:30].round(2)) # 小数点第2位まで表示
[[0.98 0.02]
[1. 0. ]
[0. 1. ]
[1. 0. ]
[1. 0. ]
[0.56 0.44]
[1. 0. ]
[1. 0. ]
[1. 0. ]
[1. 0. ]]
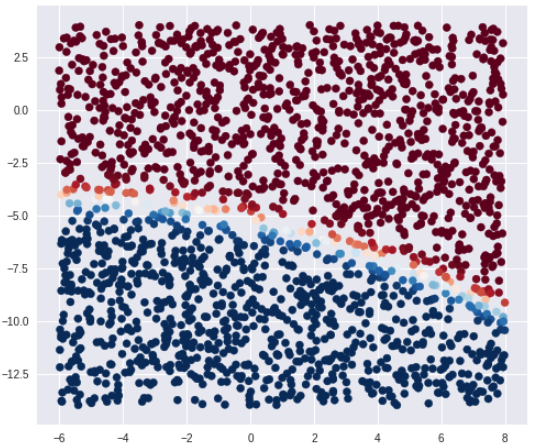
次に、確率で着色してみます。
plt.scatter(X_test[:, 0], X_test[:, 1], c=Y_prob[:, 0], s=50, cmap='RdBu')
プロットしてみると、境界付近で確率に変化があるのがわかります。
ベルヌーイ分布モデル (Bernoulli naive Bayes)
- 特徴ベクトルにベルヌーイ分布を仮定する場合に使われる。
- 入力特徴を x とした場合、 x は独立したバイナリ変数(0 または 1)となる。
- 固有パラメータは λ
事象モデル(Event Model)
P(x|C_k) = \prod_{i=1}^{n} λ_{k_i}^{x_i}(1 - λ_{k_i})^{(1-x_i)}
\\
x \in{ \{0,1 \} }\\
0 \leqq λ \leqq 1
クラス
sklearn.naive_bayes.BernoulliNB クラスを使用します。
引数(一部)
| パラメータ名 | 概要 | 備考 |
|---|---|---|
| alpha | スムージング(Laplace/Lidstone) | (初期値:1.0) ゼロ頻度問題対策 |
| binarize | バイナリ化閾値(float) | (初期値:0.0) 閾値を超える値を1、それ以外を0として扱う。 |
サンプルコード
入力 X にバイナリ変数(100次元)を設定し、BernoulliNB クラスを使って
学習・予測を行います。
import numpy as np
from sklearn.naive_bayes import BernoulliNB
X = np.random.randint(2, size=(6, 100))
Y = np.array([1, 2, 3, 4, 4, 5])
print("X[:1] =", X[:1])
model = BernoulliNB()
model.fit(X, Y)
print("Predicted Class = ", model.predict(X[2:3]))
予測結果は以下となり、クラス"3"に分類されています。
X[:1] = [[1 0 1 1 0 1 1 0 1 0 1 1 1 0 0 1 0 0 0 1 0 1 0 0 0 0 1 0 0 0 1 0 0 1 1 1
0 1 0 0 1 1 1 1 0 0 1 0 1 1 1 0 1 0 1 1 0 1 1 1 0 0 1 0 0 0 1 0 0 1 0 0
1 1 0 0 0 1 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 0 1]]
Predicted Class = [3]
多項分布モデル (Multinomial naive Bayes)
- 特徴ベクトルに多項分布を仮定する場合に使われる。
事象モデル(Event Model)
P(x|C_k) = \frac{(\sum_{i=1}^k x_i)!}{\prod_{i=1}^k x_i!}\prod_{i=1}^k p_{i}^{x_i}
x_i \geqq 0\\
p_i > 0\\
p_1 + p_2 + ... + p_k = 1
クラス
sklearn.naive_bayes.MultinomialNB クラスを使用します。
引数(一部)
| パラメータ名 | 概要 | 備考 |
|---|---|---|
| alpha | スムージング(Laplace/Lidstone) | (初期値:1.0) ゼロ頻度問題対策 |
サンプルコード
入力 X に変数(100次元)を設定し、MultinomialNB クラスを使って
学習・予測を行います。
import numpy as np
from sklearn.naive_bayes import MultinomialNB
X = np.random.randint(5, size=(6, 100))
Y = np.array([1, 2, 3, 4, 4, 5])
print("X[:1] =", X[:1])
clf = MultinomialNB()
clf.fit(X, Y)
print("Predicted Class = ", clf.predict(X[2:3]))
予測結果は以下となり、クラス"3"に分類されています。
X[:1] = [[2 3 2 2 3 2 0 2 4 4 4 0 0 3 3 2 1 2 3 1 1 2 2 0 4 0 0 4 0 4 0 4 0 0 4 2
0 3 3 3 1 4 0 3 4 2 0 1 0 0 0 1 0 4 4 1 0 1 0 3 2 1 1 1 4 0 4 1 3 3 4 3
3 3 4 2 2 3 1 0 4 0 4 1 1 3 2 0 4 4 3 4 1 0 2 2 3 0 1 3]]
Predicted Class = [3]
predict_proba() を使うと、各クラスの確率が取得出来ます。
# 各クラスの確率
Y_probs = clf.predict_proba(X[2:3])
for Y_prob in Y_probs:
for i in range(Y_prob.shape[0]):
print("Class [%d] : " % (i+1), Y_prob[i].round(2))
Class [1] : 0.0
Class [2] : 0.0
Class [3] : 1.0
Class [4] : 0.0
Class [5] : 0.0
今回は ナイーブベイズ分類器について、3つの事象モデルを試してみました。