断面にみえた!?
マンデルブロ集合の可視化表現で、「集合に含まれる部分は真っ黒(または一色)で、含まれない部分は外側に向かってグラデーションや同心円状の縞模様で」という「絵」を見たとき、なんとなく果物みたいなものを縦に割った断面を連想していました。どの果物かといわれればよくわかりませんでしたが・・・
今考えれば、ともかく、「中身が詰まった『何か』の真ん中付近がすっぽり空洞になっているようなものを縦にスパッと切った断面」を見ている、という感覚だったのだと思います。
今回の記事はこの感覚を具現化したような絵を作り、「自己満足」に浸ったときの事を思い出して書いたものです。
四元数
あるとき、四元数(quaternion)という、複素数よりもさらに複雑な数で、しかもそれがCGなどの世界で結構役にたっている事を知りました。
四元数は、その名の通り、四つの元(要素)を持つ数の事です。ちなみにマンデルブロ集合を計算する場合に基礎とした「複素数」は実部と虚部からなる「二元数」です。
四つの数の構成としては、
Q = (a, b, c, d) = a + ib + jc + kd
というものです。a,b,c,dは実数で、i,j,kは複素数でいうところの虚数単位、つまり、四元数の単位です。
i,j,kの性質は以下の掛け算規則で特徴づけられます。
i^2 = j^2 = k^2 = ijk = -1,
この性質から、四元数の単位同士や四元数同士の掛け算を求める事ができます。
四元数でマンデルブロ
複素数の2つの元を2次元の空間の座標とみなしてある計算を行い、その結果がある条件を満たす複素数の点からなる集合がマンデルブロ集合でした。
では、これと同じ方法で、つまり四元数の4つの元を4次元の空間の座標とみなして、マンデルブロ集合を計算したのと同様の繰り返し計算の収束・発散を判定して図形を書けば、何か意味のある図形が生まれるのでしょうか?
私は残念ながら、この事に関する数学的な解析をする素養を持ち合わせていないので、直観を信じ、半ば強引に、
ともかくやってみる
ことにしました。結果は4次元の座標として得られるので、これも適当に一次元を無視して(4次元を3次元に射影して)可視化してみる事にします。
c++/boostによる3次元マンデルブロ集合の計算
今回はc++/boostの四元数のライブラリを使って計算します。
# include <iostream>
# include <boost/math/quaternion.hpp>
using namespace std;
using namespace boost::math;
int main(int argc, const char * argv[])
{
for(float x = -2.0 ; x <= 2.0 ; x += 0.05 ) {
for(float y = -2.0 ; y <= 2.0 ; y += 0.05 ) {
for(float z = -2.0 ; z <= 2.0 ; z += 0.05 ) {
quaternion<float> c(x, y, z, 0);
quaternion<float> q(0, 0, 0, 0);
int i;
float r;
bool div = false;
for(i = 0; i < 20; i++) {
r = abs(q);
if(r > 4.0) {
div = true;
break;
}
q = q*q + c;
}
if(!div)
cout << x << " " << y << " " << z << endl;
}
}
}
}
コードの構造は、ほぼ、前記事「マンデルブロ集合で遊ぶ(描画編)」と同じです。発散チェックの結果を保持するdivというbool値の変数を使っています。
このプログラムをコンパイルして実行し、標準出力をファイル(tt.dat)にリダイレクとした後、gnuplotを起動し、以下のコマンドを入力します。
gnuplot> set view equal xyz
gnuplot> splot "tt.dat" with dot
1行目は、3次元プロットする場合にx,y,z座標の比率を同じにするという指定です。2行目は3次元プロットを点(dot)で表示する命令です。
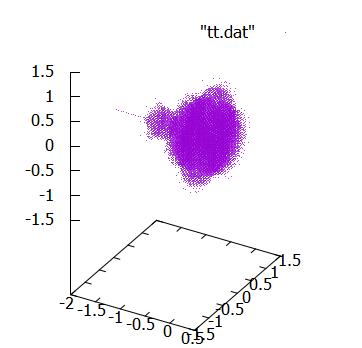
これで、以下の表示が得られます。
なんだか、三次元空間の中心に「かたまり」が浮いています。gnuplotのプロットのアウトプットウィンドウによりますが、マウスでインタラクティブに表示角度を変えられる場合には変えて、いろいろな角度からみてみてください。
この図形が、なんとなく、先がとがった回転体である事は確認できると思います。
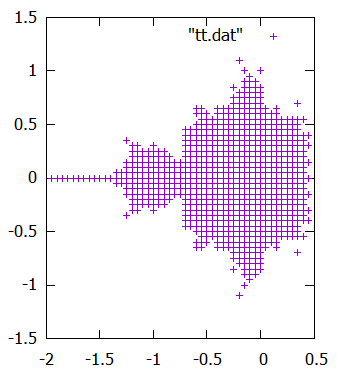
次にこれを、2次元plotしてみます。これによって、データとして出力されているz軸の要素は無視され、解像度は低いものの、おおむね見慣れた(?)マンデルブロ集合の絵になっている事が確認できます。
これは、この3次元図形の断面をみている事になります。
gnuplotのコマンドは、以下です。
gnuplot> set size ratio -1
gnuplot> plot "tt.dat"
なお、冒頭の画像は、ここまでと同様の方法で3次元画像データを作成し、ボリュームデータの可視化を行ったもので、より「断面」感が出ていると思います。
以上、です。