はじめに
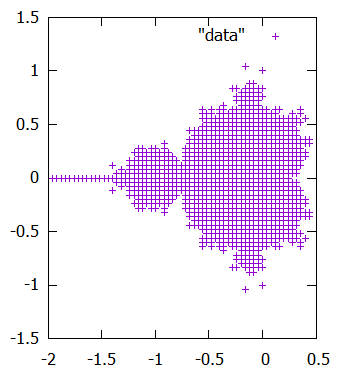
マンデルブロ集合(Mandelbrot Set)を描画すると、以下のような絵になります。
初めてみる人にとって、この図形はとても不可解で複雑、どうやったらこんな絵が描けるのか見当もつかない、と思える事でしょう。しかし、これから述べるようにこの図形のために計算するプログラムはとても短く、このような単純なプログラムからこのような絵が生成される事に驚くことと思います。
この記事では複素平面上に描かれるこの不思議な図形について、簡単な説明と実装方法を紹介します。これらを理解し、自分のものとする事で、読者が新しい開発環境(言語、ライブラリ、支援ツールなど)を習得するための道具として活用してもらえれば幸いです。
目標
- マンデルブロ集合の計算方法について理解
- マンデルブロ集合のコードを理解
- マンデルブロ集合の描画方法を理解
準備
マンデルブロ集合を描くために、いくつかの準備を行います。
複素数
複素数とは、通常私たちになじんでいる通常の数(整数、実数といった、私たちが「量」と読んでいるものを表すのに使われるもの)とは異なる面白い数です。この数は二つの部分からないます。
複素数=(実部,虚部)
実部も虚部も、実数ですから、これら2つの部分については既によく知っている「数」です。ここで、実「部」、虚「部」とあえていったのは、わけがあります。「実部」は「実数」そのもので、特に新たに知る事はありませんが、「虚部」も実数です。このようにある複素数を(a,b)のようにベクトル、または組のように書くならこれでよいですが、通常は実部の実数に「虚数単位 $i$ 」をかけた多項式で表します。つまり、
C = A + iB
この虚数単位 $i$ には次のような性質があります。
i \times i = -1
二乗する事によって $-1$ になるという意味で既に知っている実数の表現を使うなら、$\sqrt{-1}$ となります。
この性質を考慮すると、複素数の演算結果が次のようになる事がわかります。
\begin{align}
C_{1} &= A_{1} + iB_{2} , \\ C_{2} &= A_{2} + iB_{2}
\end{align}
とすると、加算は:
\begin{align}
C_{1} + C_{2} &= (A_{1} + iB_{1}) + (A_{2} + iB_{2}) \\
&= (A_{1}+A_{2}) + i(B_{1} + B_{2})
\end{align}
つまり、$(C_{1}+C_{2})$という複素数の実数部は$(A_{1}+A_{2})$、虚数部は$i(B_{1}+B_{2})$となります。
同様に、減算、乗算は:
\begin{align}
C_{1} - C_{2} &= (A_{1}-A_{2}) + i(B_{1}-B_{2}) \\
C_{1} \times C_{2} &= (A_{1} + iB_{1}) (A_{2} + iB_{2}) \\
&= A_{1}A_{2} + A_{1}(iB_{2}) + iB_{1}A_{2}+iB_{1}iB_{2} \\
&= A_{1}A_{2} + i( A_{1}B_{2} + B_{1}A_{2} ) + (-1)B_{1}B_{2} \\
&= A_{1}A_{2} - B_{1}B_{2} + i (A_{1}B_{2} + B_{1}A_{2})
\end{align}
となります。割り算は割愛します(使わないので)。
複素平面
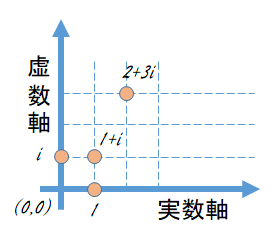
複素数の実数部と虚数部をそれぞれ、2次元直交座標上のX座標、Y座標ととらえると、すべての複素数は、この座標平面上の1つの「点」として表される事になります。
次のような複素数が複素平面上のどこにあるのか、図示してみます。
$1$
$i$
$1+i$
$2+3i$
マンデルブロ集合に含まれる?含まれない?
条件の計算方法
「集合」というからには、この集合に「含まれるもの」と「含まれないもの」があるわけです。マンデルブロ集合に含まれるかどうかを判定するには以下の条件を満たす必要があります。
条件:「複素平面上のある点$(x, y)$ について、$c = x + iy $ という複素数を考えたとき、以下の式を $n->\infty $ 、つまり、$n$を0からどんどん(無限大まで)増したとしても、$z(n)$が発散しない」
\left\{
\begin{array}{ll}
z_{0} = 0 \\
z_{n+1} = z_{n}^{2} + c
\end{array}
\right.
コード
上記条件を判定するコードを示します。
適当な疑似言語で書いてもいいのですが、以下、具体的な言語(c++)で書いてみます。
$z_{n}$が発散したかどうかは、20回程度、$z_{n}$の絶対値(実数)を計算し、それが適当な数2.0を超えるの(発散)を監視して判断します(もちろん、これらの数値は大きいほど条件の定義に忠実なものになります)。
C++(g++利用)
bool include_mandelbrot_set(complex<float> c) {
complex<float> z(0.0, 0.0);
for(int i = 0; i < 20; i++) {
if(abs(z) > 2.0) {
return false;
}
z = z * z + c;
}
return true;
}
いよいよ、描画
データ作成
まずは描画するためのデータを作成します。ここでは、マンデルブロ集合に含まれると判断された座標値をテキストファイルに書き出すというもっとも単純な方法をとります。
複素平面は無限に広がっているだけでなく、いたるところ連続なので、すべての点について、上の条件を満たしているのか、確認することはできません。なので、ここでは適当に$-2 \leq x,y \leq 2 $の範囲を調べる事にします(実はみたい範囲のマンデルブロ集合はだいたいこの範囲に収まってます)。そして、その範囲をx方向、y方向にそれぞれ100分割した点について確認し、それがマンデルブロ集合に含まれると判定されたらそのx,y座標を標準出力に書き出してみます。
繰り返し回数(今回20)、収束判定の大きさ(今回2.0)をもっと大きな数にして、精度を上げてみるとどうなるかなど、実験してみても面白いと思います。
以下がコードです。
# include <complex>
# include <iostream>
using namespace std;
// ここに include_mandelbrot_set 関数の定義を挿入
int main() {
int nx = 100;
int ny = 100;
float xmin = -2.0;
float ymin = -2.0;
float xmax = 2.0;
float ymax = 2.0;
float dx = (xmax - xmin)/(double)nx;
float dy = (ymax - ymin)/(double)ny;
for(int iy = 0; iy < ny; iy++) {
for(int ix = 0; ix < nx; ix++) {
float x = xmin + dx*(double)ix;
float y = ymin + dy*(double)iy;
complex<float> c(x, y);
if(include_mandelbrot_set(c)) {
cout << x << " " << y << endl;
}
}
}
}
コンパイル、実行は以下のようにします。
$ g++ mandelbrot.cpp -o mandelbrot
$ ./mandelbrot > data
出力先(標準出力)をリダイレクトしてファイル(data)に書き出しています。
gnuplotによる描画
このテキストデータgnuplotによって描画します。このデータファイルが置いてある場所でgnuplotを起動し、以下のコマンドを実行します。
gnuplot> set size -1
gnuplot> plot "data"
すると、以下のように表示されます。1つ目のコマンドは、x軸とy軸の比を同じにする指定です。
まとめ
この記事では、mandelbrot集合の計算のしかた、そして、データのつくり方、描画のしかたについて説明しました。
ここで紹介したコードや描画方法はもっとも素朴な(まじめな)方法だと思いますが、これをベースに、自分なりのプログラムを作成し、動かしてみてもらえればと思います。