Koch(コッホ)曲線
何はともあれ、Koch曲線はこのような「自己相似性」をもった図形です。
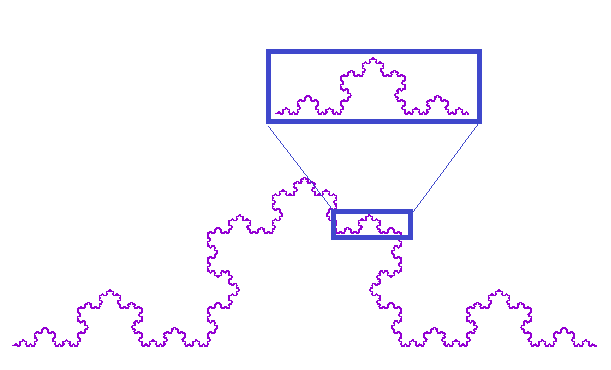
描き方の手順は以下です:
- 横(X軸方向)に長さLの直線を引く
- この線を3等分し、真ん中の直線の端を2頂点とする正三角形を描く
- 真ん中の直線(正三角形の底辺)を消す
- それぞれの辺に対して上記3ステップを適用、というのを無限に繰り返す
手作業はもちろんの事、プログラムでも、無限に繰り返す事はできないので、上記ステップを8まで繰り返した結果です。
タートルグラフィクスを使った描画コード
前に描いた記事「フラクタル図形を描く(道具編)」で紹介した簡易タートルグラフィクスライブラリのコードturtle.cxxを利用して、koch曲線を描画するコードを以下に紹介します。
// kochmain.cxx
# include <stdio.h>
# include <math.h>
void pd();
void pu();
void rt(float th);
void lt(float th);
void fd(float len);
void bk(float len);
void koch(float len, int n) {
if(n > 0) {
koch(len/3.0, n-1);
lt(60.0);
koch(len/3.0, n-1);
rt(120.0);
koch(len/3.0, n-1);
lt(60.0);
koch(len/3.0, n-1);
} else {
fd(len);
}
}
int main(int argc, char **argv)
{
pd();
rt(90.0);
koch(10.0, 6);
}
ビルド、実行は以下で。
$ g++ kochmain.cxx turtle.cxx -o kochmain
$ ./kochmain > tt.dat
描画も「フラクタル図形を描く(道具編)/描画」と同様に、gnuplotを利用します。
Koch Snow-flake
koch曲線を3つ組み合わせて、以下のような絵が描けます。
Snow-flake(雪片)や、Island(島)と呼ばれているようです。
コードはmainを以下のように書き換える事で簡単に実装できます。
int main(int argc, char **argv)
{
pd();
rt(90.0);
for(int i = 0; i < 3; i++) {
koch(10.0, 6);
rt(120.0);
}
}
koch「曲線]?
Koch曲線は、「曲線」という名前がついています。しかし、手順的にも、プログラム的にも、描いているのは「直線」だからか、何か腑に落ちないところがあります。
「無限にやったからといって曲線といって良い代物だろうか」
と。。
微分不可能
おそらく、通常我々が知っている(想定している)曲線のほとんどは、
「なめらかな」
曲線だからかもしれません。
この言葉は、数学の言葉に置き換えると、この曲線上のいたるところが「微分可能」という事になります。
あまり厳密な話に突入するつもりはありませんが、このことは、Koch曲線がどういう図形なのか、なんとなくでも想像できる鍵になると思います。
高校生くらいまでに習う、二次曲線やsin(x), cos(x)のような関数で描画する曲線は、定義域の範囲でどんな値を持ってきても、その点でその関数の「傾き」が決まります。しかし、koch曲線はそうではありません。
このような性質はフラクタルな性質を持つ図形がは往々にして持つもののようです。
フラクタル次元
そして、数学的な概念「フラクタル次元」の観点からkoch曲線を眺めるのも面白いと思います。フラクタル次元という次元は、通常我々が使う0(点),1(線),2(面),3(立体)といった「整数次元」だけでなく、その中間の「非整数次元」を取り扱います。例えば、koch曲線のフラクタル次元は、、
1.2618595
という事です(Wikipeidaより)。
今回は以上です。

