Lasso 回帰をイチから実装する

正則化 と Lasso 回帰

前回の「逆行列を使わずに最小二乗法を解く」というエントリーでは、一般の線形回帰問題
$$
\text{argmin}_\mathbf{x} \bigl\vert \mathbf{y} - \mathrm{A} \mathbf{x} \bigr\vert^2
$$
について述べました。

ただし上記の線形回帰問題は、行列Aの条件数が小さかったり、データが少なかったりすると過学習してしまいます。
過学習を防ぐため、正則化項を加えた以下のような式を最小化することも一般的です。

$$
\text{argmin}_\mathbf{x} \Bigl(\frac{1}{2}\bigl\vert \mathbf{y} - \mathrm{A} \mathbf{x} \bigr\vert^2 + \alpha |\mathbf{x}|^2\Bigr)
$$

ここで $\alpha |\mathbf{x}|^2$ が正則化項で、xの各要素があまりに大きな値にならないように抑制するものです。

正則化項には様々な種類があります。
上で述べた $\alpha |\mathbf{x}|^2$ を用いるものは Ridge 回帰と呼ばれるほか、 $\alpha |\mathbf{x}|^1 = \sum_i |x_i|$ のように１乗ノルムを用いるものをLasso回帰（Least Absolute Shrinkage and Selection Operator）と呼びます。
つまり、与えられた $\mathrm{A} \in \mathbb{R}^{N\times M}$ 、 $\mathbf{y} \in \mathbb{R}^N$ 、 $\alpha \in \mathbb{R}$ に対して

$$
\text{argmin}_\mathbf{x} \Bigl(\frac{1}{2}\bigl\vert \mathbf{y} - \mathrm{A} \mathbf{x} \bigr\vert^2 + \alpha |\mathbf{x}|^1\Bigr)
\tag{1}
$$

を求める問題です。

Lasso回帰では、多くの要素が０になるスパースな解が求まることが知られており、よく用いられています。この記事では、Lasso回帰の解き方の１つである ISTA （Iterative Shrinkage Thresholding Algorithm）を NumPy だけで実装することを目指します。これは近接勾配法の一種で、比較的高速に大規模な問題を解くことができます。

なお、Lasso回帰は Scikit-learn にも実装されているので基本的な実問題にはそちらを使う方が良いでしょう。
ただし原理を知っていると、Group Lasso や Elastic net など各問題に合わせた応用アルゴリズムも構築できるようになると思います。

まず結論

最終的に、以下の更新式を繰り返すことで最適値を求めることが可能となります。

$$
\mathbf{x} \leftarrow S_{\alpha/\rho} \Bigl(
\mathbf{x} + \frac{1}{\rho} \mathrm{A}^\top \bigl(
\mathbf{y} - \mathrm{A} \mathbf{x}
\bigr)
\Bigr)
$$

ここで、$\rho$ は学習率で、 $S_\alpha(y)$ は軟判別しきい値関数（以下で定義します）です。以下では、この導出について述べます。また、Python スクリプトも置いておきますので参考にしてください。

参考

今日からできるスパースモデリング入門

Lassoの理論と実装 -スパースな解の推定アルゴリズム-

1 次元問題

まずは以下の１次元問題を解くことを考えてみましょう。

$$
\text{argmin}_x \Bigl(\frac{1}{2}\bigl( y - x \bigr)^2 + \alpha |x|\Bigr)
$$

ここで、$y$ は任意の与えられた実数、$\alpha$ は与えられた正の実数です。絶対値の部分がややこしいですが、まずは $x <0 のときと 0\le x$ のときの２通りに分けて考えましょう。
$0\le x$ のとき、上式は
$$
\frac{1}{2}\bigl( y - x \bigr)^2 + \alpha x \\
= \frac{1}{2}(x -2 y x + 2 \alpha x + y^2) \\
= \frac{1}{2} \bigl(x - (y - \alpha)\bigr)^2 + \mathrm{const.}
$$
同様に $x < 0$ のときは
$$
\frac{1}{2}\bigl( y - x \bigr)^2 + \alpha x \\
= \frac{1}{2} \bigl(x - (y + \alpha)\bigr)^2 + \mathrm{const.}
$$
のように求まります。
$x$ の条件に注意すると、以下の3通りの状況があることに気づきます。
$$
x=S_\alpha(y)=\begin{cases}
y + \alpha & & (y < -\alpha)\\
0 & & (-\alpha \le y \le \alpha)\\
y - \alpha & & (\alpha < y)\\
\end{cases}
$$
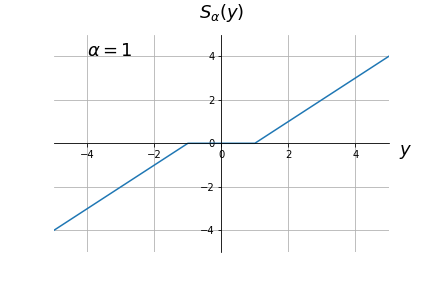
このように、 $-\alpha \le y \le \alpha$ のときは解が 0 になります。 この関数 $S_\alpha(y)$ を軟判別しきい値関数と呼びます。
軟判別しきい値関数を図示すると、以下のようになります。

多次元問題への拡張

次に、以下のように多次元に拡張することを考えましょう。 2つのベクトル、 $\mathbf{y} = [y_1, y_2, ..., y_N]$ に対して、以下を最適化するベクトル $\mathbf{x} = [x_1, x_2, ..., x_N]$ を求めます。

$$
\text{argmin}_\mathbf{x} \Bigl(\frac{1}{2}\bigl( \mathbf{y} - \mathbf{x} \bigr)^2 + \alpha |\mathbf{x}|\Bigr)
\tag{2}
$$

元の式(1)に比べると、 $\mathbf{x}$ の前に $\mathrm{A}$ が付いていないことに注意してください。この表式は以下のように分離することができます。

$$
\text{argmin}_\mathbf{x} \sum_i \Bigl( \frac{1}{2} (y_i- x_i)^2 + \alpha |x_i| \Bigr)
$$

このような問題を分離可能問題と言います。 この問題は上記の1次元問題を並列化しただけなので、
$$
x_i=S_\alpha(y_i)
$$
と解を求めることができます。

軟判別しきい値関数の Python 擬似コード

上記の軟判別しきい値関数は、以下のように実装することができます。

def soft_threshold(y, alpha):
    return np.sign(y) * np.maximum(np.abs(y) - alpha, 0.0)

蛇足になりますが、Python ではfor ループとif文を用いて実装すると非常に計算に時間がかかります。NumPy配列をインデクシングするのに時間がかかるためです。
np.sign や np.maximum を使い比較演算をベクトル化することで、効率のよい計算を実現することができます。

分離可能関数で上から抑える

さて、現在解きたい問題

$$
\text{argmin}_\mathbf{x} \Bigl(\frac{1}{2}\bigl( \mathbf{y} - \mathrm{A} \mathbf{x} \bigr)^2 + \alpha |\mathbf{x}|\Bigr)
$$
は行列Aのせいで分離可能ではありません。 ここでは何か分離可能な関数で
$$
\mathcal{L}(\mathbf{x}) = \frac{1}{2}\bigl( \mathbf{y} - \mathrm{A} \mathbf{x} \bigr)^2
$$
の部分を近似することを目指します。

二次式を上から抑える分離可能関数

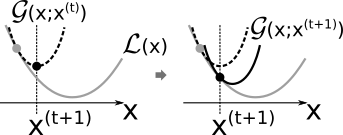
前回の「逆行列を使わずに最小二乗法を解く」 というエントリーで用いたように、以下の性質を満たす補助関数 $\mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)})$ を探すことにしましょう。

• $\mathcal{L}(\mathbf{x}^{(t)}) = \mathcal{G}(\mathbf{x}^{(t)}; \mathbf{x}^{(t)})$　： $\mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)})$ は $\mathbf{x} = \mathbf{x}^{(t)}$ で $\mathcal{L}(\mathbf{x})$ と交わる

• $\mathcal{L}(\mathbf{x}) \le \mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)})$　：　その他の点では、$\mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)})$ は $\mathcal{L}(\mathbf{x})$ より上にある

図にすると以下のような状態です。

ここで、 $\mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)})$ について、分離可能な式2のような形式のもの、つまり、　
$$
\mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)}) =
\mathcal{L}(\mathbf{x}^{(t)})
+
\frac{d\mathcal{L}(\mathbf{x}^{(t)})}{d\mathbf{x}}(\mathbf{x} - \mathbf{x}^{(t)})
+
\frac{\rho}{2}\bigl\vert\mathbf{x}-\mathbf{x}^{(t)}\bigr\vert^2 \\

\frac{\rho}{2} \Bigl\vert
\bigl(
\mathbf{x}^{(t)} - \frac{1}{\rho} \frac{d\mathcal{L}(\mathbf{x}^{(t)})}{d\mathbf{x}}
\bigr)

• \mathbf{x}
  \Bigr\vert^2 + \mathrm{const.}
  $$
  の形式のものにしておきます。 $\mathcal{L}(\mathbf{x})$ の代わりに $\mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)})$ を用いた式
  $$
  \mathbf{x}^{(t+1)} =
  \text{argmin}_\mathbf{x} \Bigl(\mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)}) + \alpha |\mathbf{x}|\Bigr)
  $$
  の最適値は、式2を参考にすると以下のように求まります。
  $$
  x^{(t+1)}_i = S_{\alpha/\rho} \Bigl(
  \mathbf{x}^{(t)} - \frac{1}{\rho} \frac{d\mathcal{L}(\mathbf{x}^{(t)})}{d\mathbf{x}}
  \Bigr)
  $$

ここで、
$\mathcal{G}(\mathbf{x}^{(t+1)}; \mathbf{x}^{(t)}) < \mathcal{L}(\mathbf{x}^{(t)})$ であることから、上記の更新式は、元のロス関数も小さくしていることが保証されます。

図にすると以下のようになります。

つまり、この更新を何度も繰り返していくことで元のロス関数である式(1)の最適解に徐々に近づいていくことになります。

なお、 $\mathcal{G}(\mathbf{x}; \mathbf{x}^{(t)})$ で用いている $\rho$ やそれを求めるための supermum_eigen 関数については前回の記事 を参考にしてください。

Lasso 更新式の Python 擬似コード

上記の操作を Python で書くと以下のようになります。

def update(x0, A, y, alpha, rho):
    """ Make an iteration with given initial guess x0 """
    res = y - A @ x0
    return soft_threshold(x0 + (A.T @ res) / rho, alpha / rho)

Pythonスクリプト

最後に、これらをまとめたPythonコードを示します。

import numpy as np

def solve_lasso(A, y, alpha, maxiter=100, tol=1.0e-4):
    """ Solve lasso problem """
    x0 = np.zeros(A.shape[1])
    rho = supermum_eigen(A.T @ A)
    x = []
    for it in range(maxiter):
        x_new = update(x0, A, y, alpha, rho)
        if (np.abs(x0 - x_new) < tol).all():
            return x_new
        x0 = x_new
    raise ValueError('Not converged.')

def update(x0, A, y, alpha, rho):
    """ Make an iteration with given initial guess x0 """
    res = y - A @ x0
    return soft_threshold(x0 + (A.T @ res) / rho, alpha / rho)

def soft_threshold(y, alpha):
    return np.sign(y) * np.maximum(np.abs(y) - alpha, 0.0)

def supermum_eigen(A):
    return np.max(np.sum(np.abs(A), axis=0))

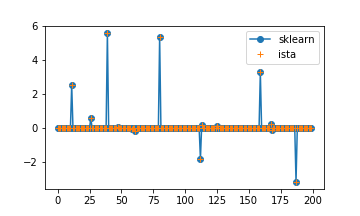
Scikit-learn の例 を参考に、以下のようにテストしました。
なお本記事では説明の都合上 $\alpha$ の定義が Scikit-learn のものと少し異なるので注意してください。

import numpy as np
import matplotlib.pyplot as plt


# Generate some sparse data to play with
np.random.seed(42)

n_samples, n_features = 50, 200
X = np.random.randn(n_samples, n_features)
coef = 3 * np.random.randn(n_features)
inds = np.arange(n_features)
np.random.shuffle(inds)
coef[inds[10:]] = 0  # sparsify coef
y = np.dot(X, coef)

# add noise
y += 0.01 * np.random.normal(size=n_samples)

# Lasso from scikit-learn
from sklearn.linear_model import Lasso

alpha = 0.1
lasso = Lasso(alpha=alpha, fit_intercept=False, tol=1.0e-5)

# Lasso from this work
alpha = 0.1 * n_samples
x = solve_lasso(X, y, alpha, tol=1e-5, maxiter=30000)

# compare
plt.plot(lasso.coef_, '-o', label='sklearn')
plt.plot(x, '+', label='ista')
plt.legend()

Scikit-learn では Coordinate descent (座標降下法) という異なるアルゴリズムを用いていますが、同じ値に収束していることがわかります。