1. Ear Clipping Triangulationとは
ビジュアルプログラミング言語のProcessingのJavascript版、「p5.js」のサンプルにSoft Body - p5.jsというものがります。ブラウザで動作確認できるのでぜひ遊んでみてほしいのですが、プリンみたいな動きをします。
これをUnityで表現するにはどうしたら良いでしょうか?
SoftBodyのソースを見ると、beginShape(); endShape(CLOSE);という関数があります。この機能がUnityには存在しません。何をしているかというと、与えられた2Dの頂点からなる図形を描写する処理をしています。
beginShape - p5.js
endShape - p5.js
この関数と同じ機能をUnityで自分で実装すれば、SoftBodyは作れるということになります。
ただ、Unityはゲームエンジンでメッシュはすべて三角形で処理されているので、与えられた頂点を三角形ポリゴンに変換しなければなりません。この記事では、複数の2D頂点から三角形ポリゴンを生成するためのアルゴリズムの一つである「Ear Clipping Triangulation」を紹介します。
1.1 先に制作物の画像紹介
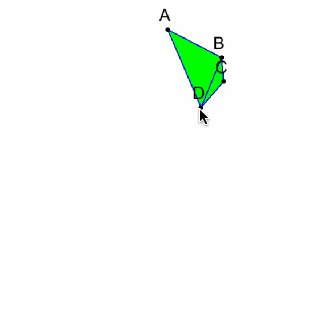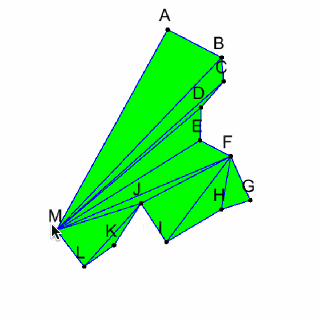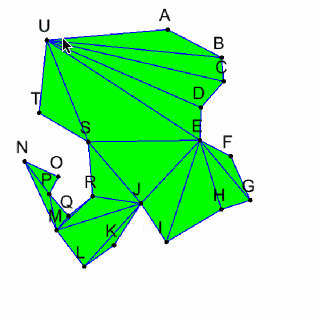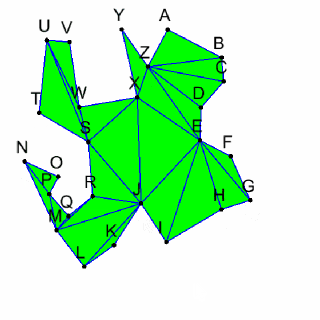
Ear Clipping Triangulationを応用してSoftBodyをUnityで作ってみました。

1.2 参考にしたページ
・Triangulation by Ear Clipping
・Soft Body - p5.js
・[Triangulator - Unity Community]
(http://wiki.unity3d.com/index.php?title=Triangulator)
・Vertex - Wikipedia
・[mapbox/earcut - Github]
(https://github.com/mapbox/earcut)
2. 必要な知識
Ear Clipping Triangulationを実装するのに必要な知識を先に紹介しておきます。
2.1 2直線のなす角が180度未満か判定する
直線OAと直線OBのなす角が180度未満か判定するとき、外積を用いると簡単に実装できます。
(Mathf.Atan2を使って実際に角度を求める方法でもできます。)
実装
// 直線OAと直線OBのなす角が180度以下か?
private static bool IsAngleLessThan180(
Vector3 o,
Vector3 a,
Vector3 b)
{
return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x) > 0;
}
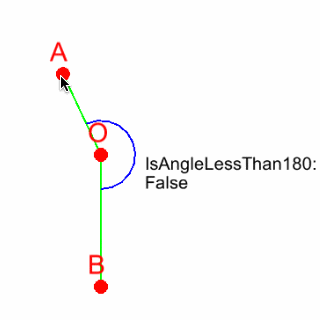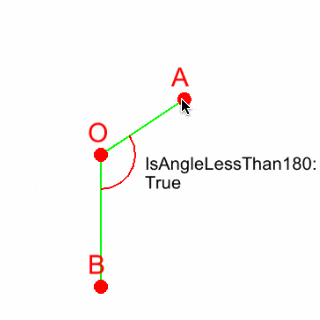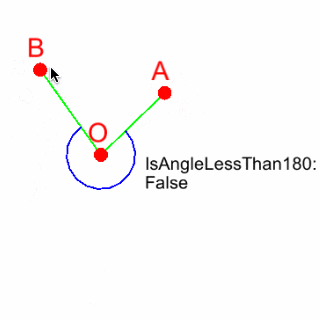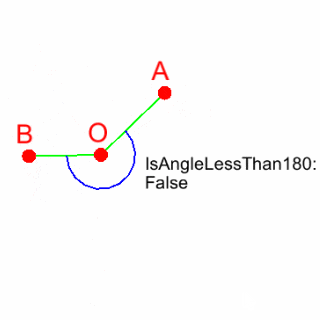
画像 直線OAと直線OBのなす角が180度以下か判定した結果
※Unityが左手系を採用しているので、左手系用の画像になります
2.2 三角形と点の当たり判定
三角形ABCと点Pの当たり判定を求める方法を紹介します。
これも外積を用いると簡単に実装できます。
以下の3つの条件で、点Pの位置関係を調べます。
- 直線ABがあるとき、点Pが、時計回り側、反時計回り側に存在するか
- 直線BCがあるとき、点Pが、時計回り側、反時計回り側に存在するか
- 直線CAがあるとき、点Pが、時計回り側、反時計回り側に存在するか
3つの条件を調べたとき、点Pが全て時計回り側、または反時計回り側に存在するときに、三角形ABCは点Pは当たり判定がTrueになります。
実装
private static bool IsContain(Vector3 a, Vector3 b, Vector3 c, Vector3 p)
{
var c1 = (b.x - a.x) * (p.y - b.y) - (b.y - a.y) * (p.x - b.x);
var c2 = (c.x - b.x) * (p.y - c.y) - (c.y - b.y) * (p.x - c.x);
var c3 = (a.x - c.x) * (p.y - a.y) - (a.y - c.y) * (p.x - a.x);
return c1 > 0f && c2 > 0f && c3 > 0f || c1 < 0f && c2 < 0f && c3 < 0f;
}
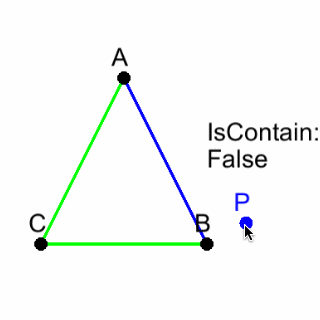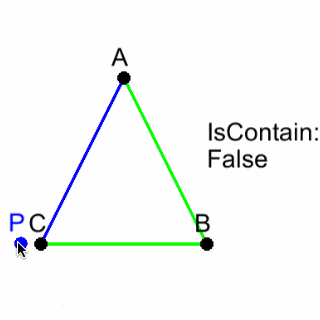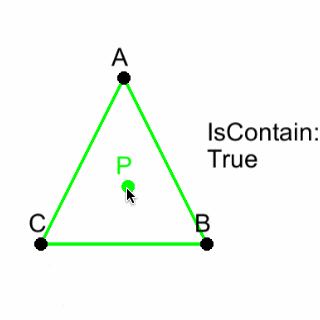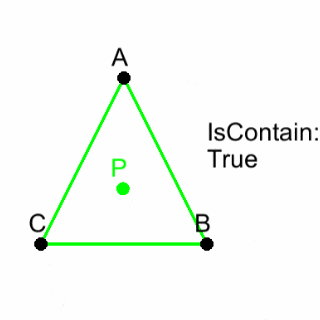
画像
直線AB、BC、CAがあるとき、
点Pが時計回り側にあれば緑色、
点Pが反時計回り側にあれば青色に設定しています。
直線AB、BC、CAが全て緑色になれば、三角形ABCと点Pは当たり判定がTrueになります。
2.3 Ear
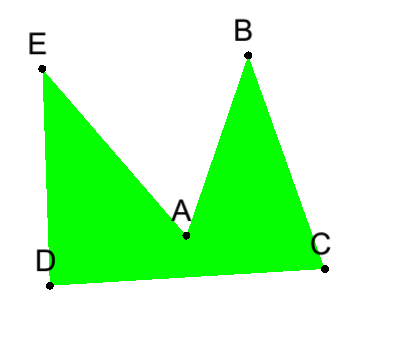
以下のような図形があるときに、隣接頂点でできる三角形を考えます。
考えられるEar候補は5点あり、点A、点B、点C、点D、点Eになります。
Earを構成する三角形は5つあり、それぞれ三角形ABC、三角形BCD、三角形CDE、三角形DEA、三角形EABになります。Ear候補からEarを検出するために以下の2つの条件を見たものを探します。
- Ear頂点で交わる2直線の内角が、180度未満である。
- Earを構成する三角形に他の頂点が含まれない
点Aは直線AEと直線ABの内角が180度以上なのでEarではありません。
点Bは三角形ABCの中に他の頂点を含まないのでEarです。
点Cは三角形BCDの中に他の頂点Aを含むのでEarではありません。
点Dは三角形CDEの中に他の頂点Aを含むのでEarではありません。
点Eは三角形DEAの中に他の頂点を含まないのでEarです。
2.4 Two ears theorem
4頂点以上で構成されたSimple Polygonには、必ず2つ以上のEarが存在するという定理です。
シンプルな定理ですが、Ear Clipping Triangulationはこの定理に基づいており、結構強力な定理なのです。
定理に基づいて2つ以上の存在するEarを取り除いた後、再びTwo ears theoremを適用することができます。
3.実装
Two ears theoremに基づいて、Earを探して取り除きます。
Earを取り除いた後の頂点リストに対して、再びTwo ears theoremに基づいて、Earを探して取り除くことを繰り返します。すべての頂点がEarになったら処理を終了します。
using System.Collections.Generic;
using UnityEngine;
namespace MeshEffect2D
{
// TODO: O(N^3) => O(N^2) のアルゴリズムに修正する
public class Triangulate
{
public static void EarCut(
IList<Vector3> vertices,
IList<int> resultIndices,
int vertexStart = 0,
int vertexCount = -1)
{
vertexCount = vertexCount < 0 ? vertices.Count : vertexCount;
if (vertexCount < 3)
{
return;
}
List<int> candidateIndices = new List<int>();
if (IsClockWise(vertices, vertexStart, vertexCount))
{
for (var i = 0; i < vertexCount; i++)
{
candidateIndices.Add(vertexStart + i);
}
}
else
{
for (var i = 0; i < vertexCount; i++)
{
candidateIndices.Add(vertexStart + vertexCount - 1 - i);
}
}
while (candidateIndices.Count >= 3)
{
var success = GetEar(vertices, candidateIndices, ref resultIndices, vertexStart, vertexCount);
if (!success)
{
break;
}
}
}
private static bool IsClockWise(IList<Vector3> vertices, int vertexStart, int vertexCount)
{
float sum = 0f;
for (int i = 0; i < vertexCount; i++)
{
Vector3 va = vertices[vertexStart + i];
Vector3 vb = (i == vertexCount - 1)
? vertices[vertexStart]
: vertices[vertexStart + i + 1];
sum += va.x * vb.y - va.y * vb.x;
}
return sum < 0;
}
private static bool GetEar(
IList<Vector3> vertices,
List<int> candidateIndices,
ref IList<int> resultIndices,
int vertexStart,
int vertexCount)
{
var hasEar = false;
for (int i = 0; i < candidateIndices.Count; i++)
{
if (candidateIndices.Count <= 3)
{
resultIndices.Add(candidateIndices[0]);
resultIndices.Add(candidateIndices[1]);
resultIndices.Add(candidateIndices[2]);
candidateIndices.RemoveRange(0, 3);
return true;
}
var length = candidateIndices.Count;
var indexA = candidateIndices[(i + length - 1) % length];
var indexB = candidateIndices[i];
var indexC = candidateIndices[(i + 1) % length];
var vertexA = vertices[indexA];
var vertexB = vertices[indexB];
var vertexC = vertices[indexC];
if (!IsAngleLessThan180(vertexB, vertexA, vertexC))
{
continue;
}
var isEar = true;
for (var j = 0; j < vertexCount; j++)
{
if (vertexStart + j == indexA
|| vertexStart + j == indexB
|| vertexStart + j == indexC)
{
continue;
}
var vp = vertices[vertexStart + j];
if (IsContain(vertexA, vertexB, vertexC, vp))
{
isEar = false;
break;
}
}
if (isEar)
{
hasEar = true;
resultIndices.Add(indexA);
resultIndices.Add(indexB);
resultIndices.Add(indexC);
candidateIndices.RemoveAt(i);
i -= 1;
}
}
if (!hasEar)
{
return false;
}
return true;
}
private static bool IsContain(Vector3 a, Vector3 b, Vector3 c, Vector3 p)
{
var c1 = (b.x - a.x) * (p.y - b.y) - (b.y - a.y) * (p.x - b.x);
var c2 = (c.x - b.x) * (p.y - c.y) - (c.y - b.y) * (p.x - c.x);
var c3 = (a.x - c.x) * (p.y - a.y) - (a.y - c.y) * (p.x - a.x);
return c1 > 0f && c2 > 0f && c3 > 0f || c1 < 0f && c2 < 0f && c3 < 0f;
}
private static bool IsAngleLessThan180(
Vector3 o,
Vector3 a,
Vector3 b)
{
return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x) > 0;
}
}
}
Ear Clipping Triangulationを工夫なく実装するとO(n ^ 3)になってしまいました。
論文にはここからO(n ^ 2)にする方法が書いてあるので、時間があるときに、やってみます。
4.動作確認
4.1 Ear Clipping Triangulation
Ear Clipping Triangulationの動作確認をしてみます。
このアルゴリズムはSimplePolygonのみでしか使えないので、自己交差ポリゴンになっているときに、ポリゴンがおかしくなります。
画像 Ear Clipping Triangulationの動作確認
4.2 SoftBody
次にSoft Bodyの実装をしてみます。
実装方法はp5.jsのサンプルスクリプトをご覧ください。
Unityで実装してみたらこんな感じになりました。
いい感じなきがします。
画像 UnityでSoftBodyを実装してみました。
5. まとめ・発展
Ear Clipping Triangulationを用いると、Processingで用いられるbeginShape、endShapeを使った表現ができるようになります。Triangulation by Ear Clippingの論文にはHoleの作り方も書いてあるので、それを実装するのも面白そうです。また、このアルゴリズムの計算量はO(n^2)ですが、O(n*log n)で計算できるアルゴリズムやそれ以下の計算量のアルゴリズムもあります。リッチな表現を実現するためにより計算量の低いアルゴリズムを勉強したくなりますね。
この記事はここでおしまいです。
またどこかでお会いしましょう。