この記事は…
技術評論社の『強化学習理論入門』にでてくる「ポリシー反復法」を使って、実際に計算しながら迷路を解いていく内容となっています。はじめからあまり複雑にすると混乱してしまうので、例を簡単にして説明していきます。
やりたいことは、3×3セル で構成される環境における、スタートからゴールまでの経路探索です。まずは何の障害物もない環境を用意して、左上のスタートから右下のゴールまでの経路を探索します。
なお、このアルゴリズムを元にVBAで実装したサンプルは こちら で公開しています。
準備
環境設定
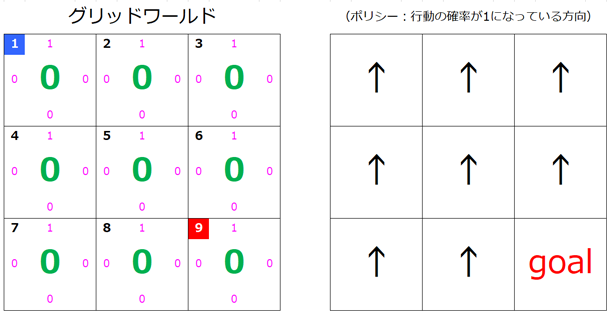
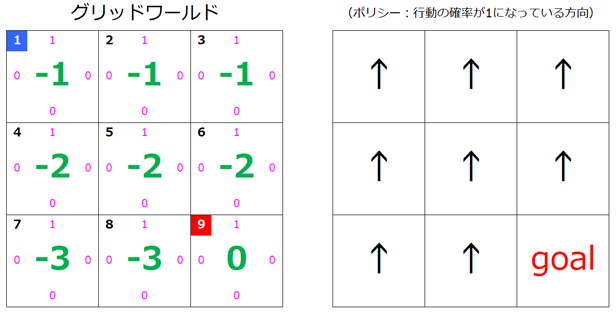
今回は簡単のため、以下のような 3×3 のグリッドワールドで話を進めます。
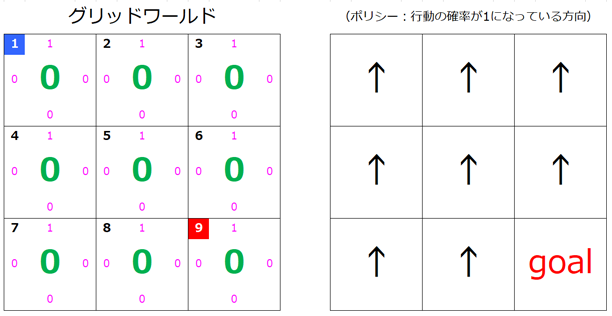
それぞれのセルの左上の数はそのセルを表す番号で、状態 S を表す数ともいいます。
例えば、左上のセルには「1」が振られていますが、このセルを 状態 s=1 もしくは単に s=1 と表します。
s=5 だと真ん中のセルですね。
s=1 は青にしていますが、これはスタートを表しています。
s=9 は赤にしていますが、これはゴールを表しています。
セルの四方に配置されているピンク色の値は、その方向への移動を選択する場合の 確率 です。
s=1 では、上が「1」、それ以外は「0」になっているので、このセルでは必ず上向きに移動を試みます。
この値は最終的には正しい方向の値が「1」になります。
セルの真ん中の緑の値は、そのセルの 価値 を表しています。
この値も徐々に更新されていきます。
右側の矢印の図は各セルでどの方向に移動するかを表しています。
これはピンク色の値が「1」になっている方向です。
スタート地点からこの矢印をたどっていくとゴールまでたどり着くようにするのが今回の目的です。
アルゴリズム
具体的な計算に入る前にざっくりとしたアルゴリズムを説明します。
1. 自分のいるセル(状態)の価値を計算
自分のいるセル(状態)の価値を計算します。上下左右に設定されている移動確率で移動した場合の報酬、移動先セル(状態)の価値を元に計算します。すべてのセル(状態)について行います。
2. どの方向に行けばよいかを調べる
自分のセル(状態)からどちらの方向に行けばもっとも高い価値を得られるかを調べます。
3. 行動ポリシーを更新する
もっとも高い価値を得られる方向への移動確率を「1」にし、他の方向への移動確率を「0」にします。
4. 繰り返す
移動方向の更新がなくなるまで 1. ~ 3. を繰り返します。
ベルマン方程式と行動-状態価値関数
アルゴリズムで利用する計算式をあげておきます。
アルゴリズムの「1.」での計算にはベルマン方程式を、「2.」での計算では行動-状態価値関数を利用します。
実際にはわかっている値を代入していくだけです。
見比べるとわかりますが、行動-状態価値関数はベルマン方程式の後半部分と同じです。
ベルマン方程式
V_{\pi}(s)=\sum_{a}\pi(a|s)\sum_{(r,s')}p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\}
行動-状態価値関数
q_{\pi}(s,a)=\sum_{(r,s')}p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\}
各項目について
ベルマン方程式と行動-状態価値関数の各項目が何を表していてどんな値をとるかについてみていきます。
-
$V_{\pi}(s)$
セル(状態)s の価値を表します。
例えば、現時点の s=1 の価値(緑の数値)は 0 なので、$V_{\pi}(1)=0$です。 -
${\pi}(a|s)$
状態 s で取りうる行動 a の確率(ピンクの数値)を表します。
例えば、s=1 の場合、上が 1 、それ以外は 0 なので、それぞれ
$\qquad\pi(↑|1)=1, \quad\pi(→|1)=0, \quad\pi(↓|1)=0, \quad\pi(←|1)=0$
となります。
その状態で取りうる行動についての総和を求めるため $\sum$ がついています。 -
$p(r,s'|s,a)$
その状態で取った行動で報酬(r)を得て次の状態(s')になる確率です。
今回は例えば右に移動しようとした場合は確率「1」で右に移動することとします。
環境によっては、ある確率によって結果が変わる場合があり、すべての可能性について計算するため $\sum$ で総和をとっています。 -
$r$
状態 s で行動 a を取った際に得られる報酬です。 -
$\gamma$
割引率と呼ばれるハイパーパラメータです。
今回は有限回の手順でゴールまで到達することが保証されているので 1 としています。 -
$V_{\pi}(s')$
状態 s で行動 a を取った際の移動先の状態の価値です。
グリッドワールドの設定
今回の説明で使用するグリッドワールドの報酬等の設定は以下の通りとします。
ゴールにいる時は確率「1」で報酬「0」を得て状態はそのままとなります。
つまり、ゴールに到達しているのでそれ以上変化しないということですね。
移動先がワールド内の場合は、確率「1」で報酬「-1」を得て移動先のセル(状態)に移動します。
移動先がワールド外に行ってしまう場合、例えば $s=1$ で上や左に移動する場合ですが、
その場合も、確率「1」で報酬「-1」を得ます。ただし、移動先は元のセル(状態)のままとなります。
報酬を「-1」に設定しているのは、なるべく少ない手数でゴールまでたどり着くルートを探索するためです。
表にまとめると以下のようになります。
| 場合 | 確率($p$) | 報酬($r$) | 次の状態($s'$) |
|---|---|---|---|
| ゴールにいる時 | 1 | 0 | そのまま |
| 移動先がワールド内の場合 | 1 | -1 | 移動先 |
| 移動先がワールド外の場合 | 1 | -1 | 移動前の場所に戻る |
計算実行
1. 価値の計算:1回目
では、準備が整ったので実際に計算してルートを探索してみましょう。
価値の計算にはベルマン方程式を用います。
【ベルマン方程式】
V_{\pi}(s)=\sum_{a}\pi(a|s)\sum_{(r,s')}p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\}
まずは現在の状態です。
各状態($s$)の価値は「0」、行動($a$)の確率はすべて上方向が「1」になっています。
s=1のとき
- $a=「↑」$
まずは上に移動する場合です。状態 $s=1$ のときは上向きの行動確率が「1」になっています。そして、状態 $s=1$ で 行動 $a=↑$ をとると(上に移動しようとすると)、ワールド外に移動してしまいます。よって、「グリッドワールドの設定」表より、確率 $p=1$ で報酬 $r=-1$ を得て、次の状態は移動前のセル($s'=1$)となります。ベルマン方程式に実際の値をあてはめてみると…
\begin{align}
& \pi(a|s)=\pi(a=↑|s=1)=1 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(1)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=↑|s=1)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(1)\bigr\} \\
\\
& =1*1* \bigl\{-1+1*0 \bigr\} \\
\\
& =-1
\end{align}
- $a=「→」$
次は右に移動する場合です。右向きの行動確率は「0」です。そして 行動 $a=→$ をとると $s=2$ に移動します。移動先はワールド内なので、「グリッドワールドの設定」表より、確率 $p=1$ で報酬 $r=-1$ を得て、次の状態は移動先のセル($s'=2$)となります。値をあてはめてみると…
\begin{align}
& \pi(a|s)=\pi(a=→|s=1)=0 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(2)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=→|s=1)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(2)\bigr\} \\
\\
& =0*1* \bigl\{-1+1*0 \bigr\} \\
\\
& =0
\end{align}
- $a=「↓」$
次は下に移動する場合です。下向きの場合は移動先が $s=4$ になるだけで他は左向きの場合とほぼ同じですね。値をあてはめてみると…
\begin{align}
& \pi(a|s)=\pi(a=↓|s=1)=0 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(4)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=↓|s=1)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(4)\bigr\} \\
\\
& =0*1* \bigl\{-1+1*0 \bigr\} \\
\\
& =0
\end{align}
- $a=「←」$
最後は左に移動する場合です。この場合、移動先はワールド外になるので、上向きの場合と同じです。ただし、移動確率は「0」なのでその部分だけ異なります。値をあてはめてみると…
\begin{align}
& \pi(a|s)=\pi(a=←|s=1)=0 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(1)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=←|s=1)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(1)\bigr\} \\
\\
& =0*1* \bigl\{-1+1*0 \bigr\} \\
\\
& =0
\end{align}
- 価値の計算
状態 $s=1$ におけるすべての行動についての値が算出できたので総和を求めます。この値が更新された状態 $s=1$ の価値となります。
V_{\pi(1)} = -1 + 0 + 0 + 0 = -1
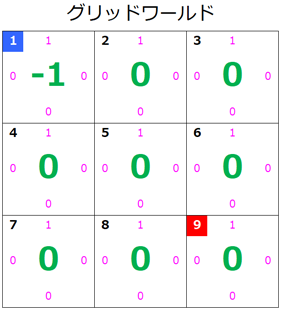
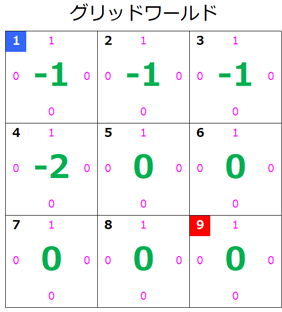
- 更新されたグリッドワールド
状態 $s=1$ の価値が更新されたのでグリッドワールドはこのようになります。
s=2のとき
- $a=「↑」$
上に移動する場合です。状態 $s=2$ のときも $s=1$ のときと同様、上向きの行動確率が「1」になっています。それぞれの値も $s=1$ のときと同じですね。
\begin{align}
& \pi(a|s)=\pi(a=↑|s=2)=1 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(2)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=↑|s=2)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(2)\bigr\} \\
\\
& =1*1* \bigl\{-1+1*0 \bigr\} \\
\\
& =-1
\end{align}
- $a=「→」$
行動 $a=→$ をとると $s=3$ に移動します。値をあてはめてみると…
\begin{align}
& \pi(a|s)=\pi(a=→|s=2)=0 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(3)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=→|s=2)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(3)\bigr\} \\
\\
& =0*1* \bigl\{-1+1*0 \bigr\} \\
\\
& =0
\end{align}
- $a=「↓」$
下に移動する場合も $s=1$ のときと同じですね。
\begin{align}
& \pi(a|s)=\pi(a=↓|s=2)=0 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(5)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=↓|s=1)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(5)\bigr\} \\
\\
& =0*1* \bigl\{-1+1*0 \bigr\} \\
\\
& =0
\end{align}
- $a=「←」$
左に移動する場合です。この場合、移動先は $s=1$ になり $s=1$ の価値は先ほど更新されているので注意が必要です。とはいえ、移動確率は「0」なので結果は 0 になりますが…
\begin{align}
& \pi(a|s)=\pi(a=←|s=2)=0 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(1)=-1 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=←|s=2)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(1)\bigr\} \\
\\
& =0*1* \bigl\{-1+1*-1 \bigr\} \\
\\
& =0
\end{align}
- 価値の計算
状態 $s=2$ におけるすべての行動についての値が算出できたので総和を求めます。この値が更新された状態 $s=2$ の価値となります。
V_{\pi(2)} = -1 + 0 + 0 + 0 = -1
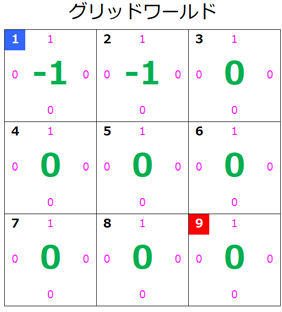
- 更新されたグリッドワールド
状態 $s=2$ の価値が更新されたのでグリッドワールドはこのようになります。
s=3のとき
$s=1, s=2$ とほぼ同じなので結果だけ示します。
V_{\pi(3)} = -1 + 0 + 0 + 0 = -1
s=4のとき
- $a=「↑」$
状態 $s=4$ で上に移動する場合です。上向きの行動確率が「1」で、状態 $s=4$ で 行動 $a=↑$ をとると 確率 $p=1$ で報酬 $r=-1$ を得て $s=1$ に移動します。$s=1$ の価値が -1 になっていることに注意します。
\begin{align}
& \pi(a|s)=\pi(a=↑|s=4)=1 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(1)=-1 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=↑|s=4)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(1)\bigr\} \\
\\
& =1*1* \bigl\{-1+1*-1 \bigr\} \\
\\
& =-2
\end{align}
-
$a=「→」, a=「↓」, a=「←」$
行動確率はともに「0」なので、計算結果は 0 になります。 -
価値の計算
状態 $s=4$ の価値を更新します。
V_{\pi(4)} = -2 + 0 + 0 + 0 = -2
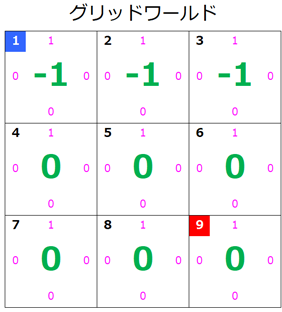
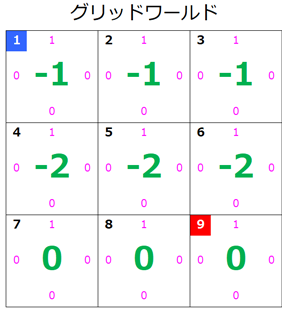
- 更新されたグリッドワールド
状態 $s=4$ の価値が更新されたのでグリッドワールドはこのようになります。
s=5のとき
いままでの計算とあまり変わりがないので結果だけ示します。
V_{\pi(5)} = -2 + 0 + 0 + 0 = -2
s=6のとき
-
$a=「↑」$
$s=4$ と同様、-2 になります。 -
$a=「→」$
行動確率は「0」なので、計算結果は 0 になります。 -
$a=「↓」$
行動確率が「0」なので、計算結果は 0 になりますが、移動先が $s=9$ のゴールになるので、報酬等が「グリッドワールドの設定」表のどれに該当するかについて補足します。$s=6$ からみた「ゴール」はあくまでも移動先なので、報酬等は「グリッドワールドの設定」表の「ゴールにいる時」ではなく「移動先がワールド内の場合」となります。よって、
\begin{align}
& \pi(a|s)=\pi(a=↓|s=6)=0 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(9)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=↓|s=6)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(9)\bigr\} \\
\\
& =0*1* \bigl\{-1+1*0 \bigr\} \\
\\
& =0
\end{align}
-
$a=「←」$
行動確率は「0」なので、計算結果は 0 になります。 -
価値の計算
状態 $s=6$ の価値を更新します。
V_{\pi(6)} = -2 + 0 + 0 + 0 = -2
- 更新されたグリッドワールド
状態 $s=6$ の価値が更新されたのでグリッドワールドはこのようになります。
s=7のとき
- $a=「↑」$
いままで同様、状態 $s=7$ で 行動 $a=↑$ をとると 確率 $p=1$ で報酬 $r=-1$ を得て $s=4$ に移動します。$s=4$ の価値が -2 になっていることに注意します。
\begin{align}
& \pi(a|s)=\pi(a=↑|s=7)=1 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(4)=-2 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=↑|s=4)*p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(4)\bigr\} \\
\\
& =1*1* \bigl\{-1+1*-2 \bigr\} \\
\\
& =-3
\end{align}
-
$a=「→」, a=「↓」, a=「←」$
行動確率はともに「0」なので、計算結果は 0 になります。 -
価値の計算
状態 $s=7$ の価値を更新します。
V_{\pi(7)} = -3 + 0 + 0 + 0 = -3
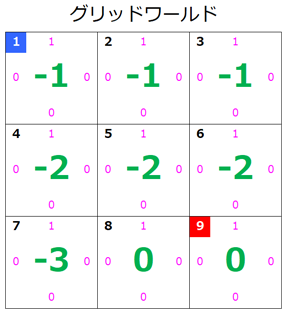
- 更新されたグリッドワールド
状態 $s=7$ の価値が更新されたのでグリッドワールドはこのようになります。
s=8のとき
いままでの計算とあまり変わりがないので結果だけ示します。
V_{\pi(8)} = -3 + 0 + 0 + 0 = -3
s=9のとき
ゴール地点の場合です。ゴールにいる場合、「グリッドワールドの設定」表に従うと確率 $p=1$ で報酬 $r=0$ を得てその場にとどまることとなります。報酬 $r=0$ かつ $V_{\pi}(S')=V_{\pi}(9)=0$ なので、中かっこ{ }の中は 0 になります。よって、計算結果は 0 になります。
念のため、$a=↑$ の場合の計算式をあげておきます。
\begin{align}
& \pi(a|s)=\pi(a=↑|s=9)=1 \\
\\
& p(r,s'|s,a)=1 \\
\\
& r=0 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(9)=0 \\
\\
よって
\\
& \pi(a|s)*p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =\pi(a=↑|s=9)*p(r,s'|s,a)\bigl\{0+\gamma V_{\pi}(9)\bigr\} \\
\\
& =1*1* \bigl\{0+1*0 \bigr\} \\
\\
& =0
\end{align}
- 価値の計算
状態 $s=9$ の価値を計算します。
V_{\pi(9)} = 0 + 0 + 0 + 0 = 0
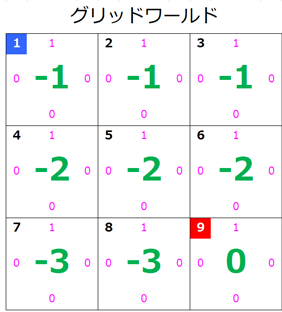
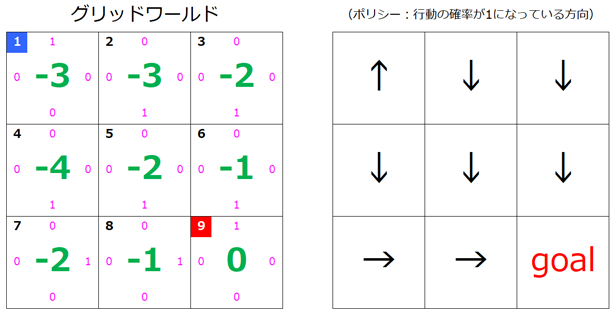
- 最終的なグリッドワールド
最終的なグリッドワールドはこのようになります。
2.と3. どの方向に行けばよいかを調べて行動ポリシーを更新する:1回目
さて、すべての状態の価値が更新されたので、次はすべての状態(セル)について、どの方向に行けばよいかを状態-価値関数を使って調べ、行動ポリシーを更新します。(どの方向の行動確率を「1」にすればよいかを決めます。)
【行動-状態価値関数】
q_{\pi}(s,a)=\sum_{(r,s')}p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\}
s=1のとき
- $a=「↑」$
状態 $s=1$ で 行動 $a=↑$ をとるとワールド外に移動してしまいます。よって、「グリッドワールドの設定」表より、確率 $p=1$ で報酬 $r=-1$ を得て、次の状態は移動前のセル($s'=1$)となります。計算方法はベルマン方程式の場合とほぼ同じですね。
\begin{align}
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(1)=-1 \\
\\
よって
\\
& p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(1)\bigr\} \\
\\
& =1* \bigl\{-1+1*-1 \bigr\} \\
\\
& =-2
\end{align}
- $a=「→」$
行動 $a=→$ をとる場合の移動先はワールド内です。よって、「グリッドワールドの設定」表より、確率 $p=1$ で報酬 $r=-1$ を得て、次の状態は右隣りのセル($s'=2$)となります。
\begin{align}
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(2)=-1 \\
\\
よって
\\
& p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(2)\bigr\} \\
\\
& =1* \bigl\{-1+1*-1 \bigr\} \\
\\
& =-2
\end{align}
- $a=「↓」$
行動 $a=↓$ をとる場合の移動先は $s'=4$ となります。状態4 の価値は「-2」であることに注意します。
\begin{align}
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(4)=-2 \\
\\
よって
\\
& p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(4)\bigr\} \\
\\
& =1* \bigl\{-1+1*-2 \bigr\} \\
\\
& =-3
\end{align}
- $a=「←」$
行動 $a=←$ をとる場合の移動先はワールド外となります。
\begin{align}
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(1)=-1 \\
\\
よって
\\
& p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(1)\bigr\} \\
\\
& =1* \bigl\{-1+1*-1 \bigr\} \\
\\
& =-2
\end{align}
- もっとも大きい値となる 行動a を採用する
$\quad a=↑$ のとき -2
$\quad a=→$ のとき -2
$\quad a=↓$ のとき -3
$\quad a=←$ のとき -2
このなかでもっとも大きい値をとる 行動a を $s=1$ の行動ポリシーとしますが、もっとも大きい値である「-2」をとる行動は 3種類 あります。今回は簡単のため $a=「↑」$ を行動ポリシーとして採用します。(上方向の行動確率を「1」にします。)
今回は変化はありませんね。
s=2, s=3, s=4, s=5
$s=2$ から $s=5$ までは $s=1$ と同様の結果となるので省略します。
s=6のとき
- $a=「↑」$
\begin{align}
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(3)=-1 \\
\\
よって
\\
& p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(3)\bigr\} \\
\\
& =1* \bigl\{-1+1*-1 \bigr\} \\
\\
& =-2
\end{align}
- $a=「→」$
\begin{align}
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(6)=-2 \\
\\
よって
\\
& p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(6)\bigr\} \\
\\
& =1* \bigl\{-1+1*-2 \bigr\} \\
\\
& =-3
\end{align}
- $a=「↓」$
移動先は $s=9$ でゴールになりますが、状態の価値を計算したときと同様、あくまでもワールド内の移動なので、報酬等は「移動先がワールド内の場合」となります。
\begin{align}
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(9)=0 \\
\\
よって
\\
& p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(9)\bigr\} \\
\\
& =1* \bigl\{-1+1*0 \bigr\} \\
\\
& =-1
\end{align}
- $a=「←」$
\begin{align}
& p(r,s'|s,a)=1 \\
\\
& r=-1 \\
\\
& \gamma=1 \\
\\
& V_{\pi}(s')=V_{\pi}(5)=-2 \\
\\
よって
\\
& p(r,s'|s,a)\bigl\{r+\gamma V_{\pi}(s')\bigr\} \\
\\
& =p(r,s'|s,a)\bigl\{-1+\gamma V_{\pi}(5)\bigr\} \\
\\
& =1* \bigl\{-1+1*-2 \bigr\} \\
\\
& =-3
\end{align}
- もっとも大きい値となる 行動a を採用する
$\quad a=↑$ のとき -2
$\quad a=→$ のとき -3
$\quad a=↓$ のとき -1
$\quad a=←$ のとき -3
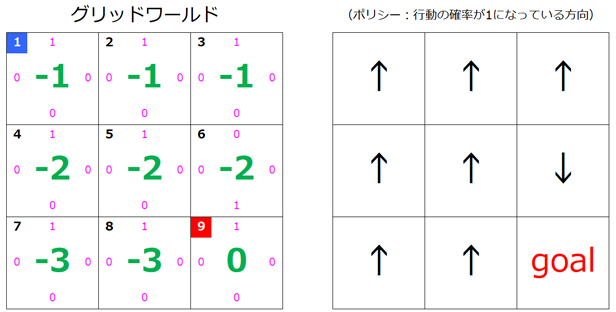
このなかでもっとも大きい値をとる 行動a は下向きの移動ですね。なので $s=6$ の行動ポリシーとしては、$a=「↓」$ が採用されます。
$s=6$ の矢印が下向きに更新されたのが確認できると思います。
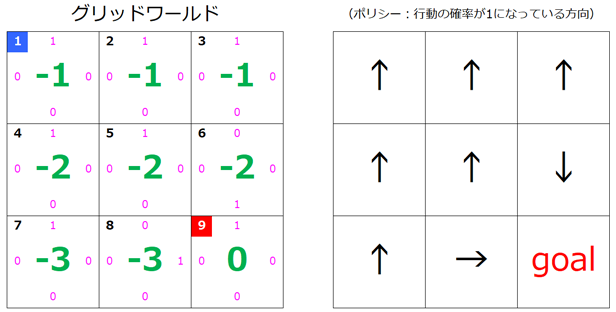
s=7, s=8
こちらも更新された図だけ示すことにします。$s=8$ の矢印が右向きに更新されていますね。
4. 繰り返す
以降はここまでの計算(1. ~ 3.)を繰り返します。
計算の仕方自体は同じなので更新後のグリッドワールドの状態だけを示すことにします。
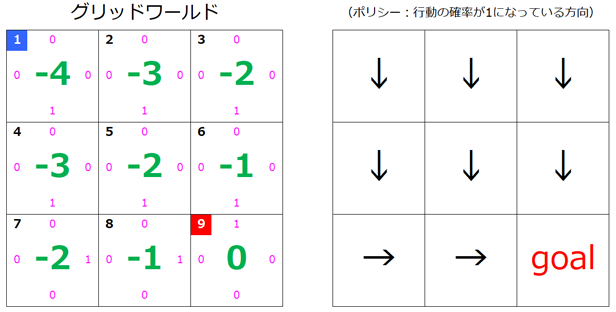
2回目の更新後
$s=3, s=5, s=7$ の矢印の向きが変化したのがわかります。
3回目の更新後
$s=2, s=4$ も変化しました。
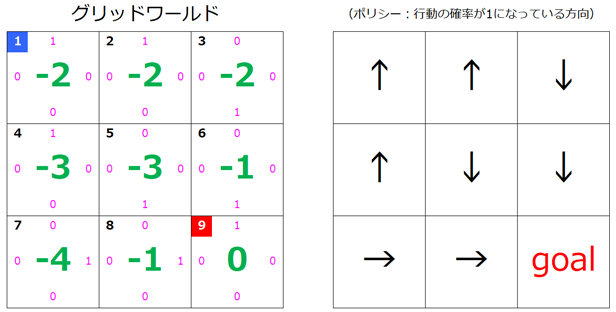
4回目の更新後
$s=1$ も変化しました。
5回目
計算するとわかりますが、これ以上、行動ポリシーは更新されません。よって、4回目で更新完了となります。
ちゃんとスタートからゴールまでいけるか確かめてみる
さて、この結果が正しくゴールまで導かれるようなルートになっているか確かめてみましょう。
まず、スタートの $s=1$ の行動ポリシーは $a=↓$ となっているので $s=4$ に移動します。
$s=4$ の行動ポリシーも $a=↓$ になっているので $s=7$ に移動します。
$s=7$ の行動ポリシーは $a=→$ なので $s=8$ に移動します。
$s=8$ の行動ポリシーも $s=→$ なので $s=9$ に移動します。
無事にゴールまでたどり着けました。
もう少し迷路っぽい環境で試してみる
行き止まりも何もない環境では面白みがないですよね。なのでもう少し迷路っぽい環境で試してみましょう。
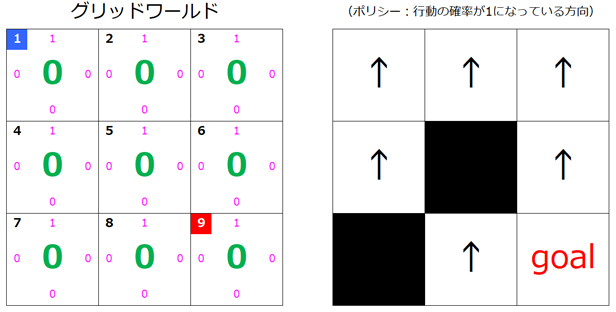
環境
黒い部分は通行不可能なセルで、そちら向きに移動しようとすると元のセルに戻されてしまいます。動きとしてはワールド外に出てしまう場合と同じですね。先ほど求めた行動ポリシーではスタートから下向きに移動してその後、右に移動するようになっていたので、今回はその方向には行けないようにしてみました。
計算の過程は省略しますが、行動ポリシーがどのように更新されるか見ていきましょう。
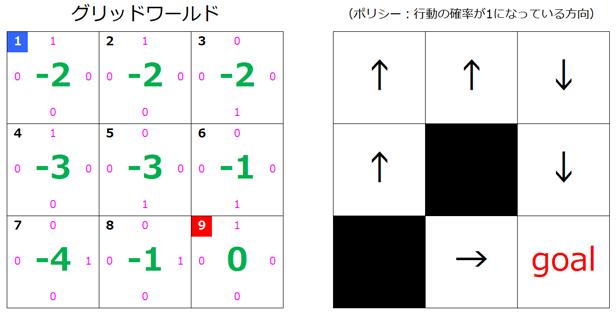
1回目
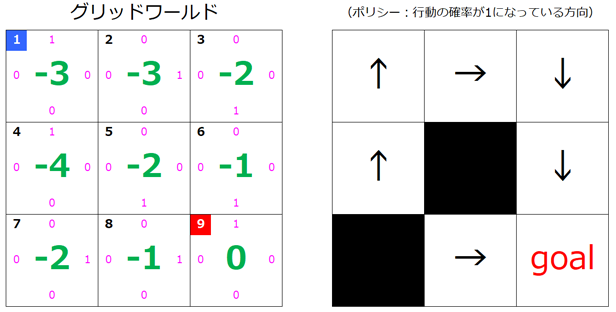
2回目
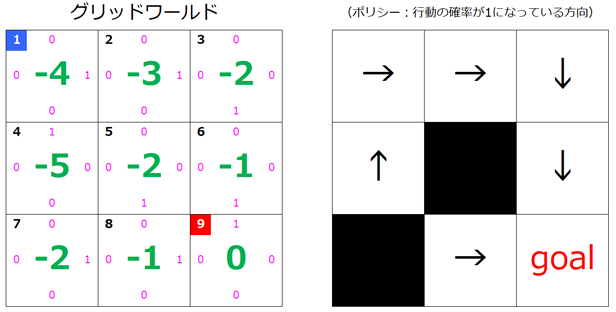
3回目
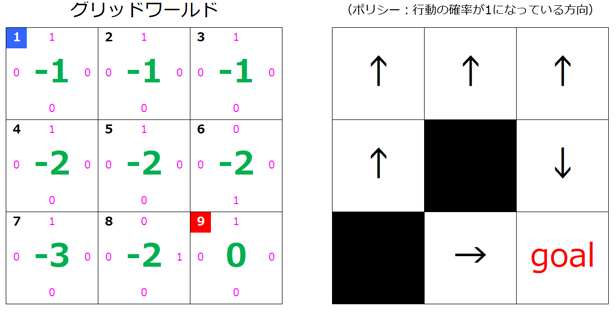
4回目
これ以上は更新されないので、これで完了です。
ルートの確認
矢印をたどると、ちゃんとスタートからゴールまで到達できていますね。
まとめみたいなの
今回は左上のセルをスタートに設定しましたが、実は結果を見るとどのセルからスタートしてもゴールに到達できるのがわかると思います。
また、3×3 よりも大きなグリッドワールドでもこの手順でゴールまでの経路を探索することが可能です。
今回は「ポリシー反復法」というアルゴリズムを使いましたが、より手順の簡単な「価値反復法」というアルゴリズムもあるようですので、興味がある方はぜひ試してみましょう。
参考書籍
『強化学習理論入門』