コンパイラ 作りながら学ぶ 第2章

コンパイラ作りながら学ぶ（著者　中田育男）　で勉強したことを自分の言葉でまとめています．
https://www.ohmsha.co.jp/book/9784274221163/

2.1 後置記法

後置記法は演算子を後ろに置く記法．通常の算術式ではaとbの加算は

a+b

のように演算子の「+」を中に置く形となる．この記法は中置記法と呼ばれる．これに対して後置記法は

ab+

のように演算子が後ろに置かれる．反対に前置記法では，

+ab

のように演算子を前に置く．前置法はポーランド人が考え出した記法なので，ポーランド記法と呼ばれる．後置記法は演算子の位置が逆であるため逆ポーランド記法と呼ばれる．

次に，より複雑な式の際に，後置記法ではどのように表されるのかを説明する．例えば以下のような式があった時，

a*b+c*d+e*f

後置記法では以下のように表される．

ab*cd*+ef*+

後置記法の優れている点は，式を左から順に読んで計算すれば，その式が示す値を計算出来てしまうという点である．具体的にはスタックを用いて計算されるが，それは2章の最後で説明されている．後置記法から手計算で式の値を計算する場合,基本的に演算子が現れたら直前2つの演算数を計算し，それを一つの演算数として書き換える，ということを繰り返す．上の式を例に挙げると以下のような変形となる．

ab*cd*+ef*+
(a*b)cd*+ef*+
(a*b)(c*d)+ef*+
((a*b)+(c*d))(e*f)+
((a*b)+(c*d))+(e*f)

まず，abを読み込み，演算子「*」が現れたため，直前2つの演算数a,bを用いてab*を(ab)と置き換える．次に，同様にしてcd*を(cd)へと置き換える．次に演算子「+」が現れたため，直前2つの演算数(ab),(cd)を用いて(ab)+(cd)へと置き換える．次に，efを(ef)へ置き換える．次に，演算子「+」が現れたため直前二つの演算数，(ab)+(cd),(ef)を加算して((ab)+(cd))+(e*f)が導かれる．

次に中置記法から後置記法へ変換する方法を説明する．まず，中置記法を後置記法へと変換する関数Pを考えた時，その関数Pは以下のような挙動をする．
$$P(式1 ;演算子; 式2) = P(式1);P(式2);演算子, \qquad
P(演算数) = 演算数$$

右辺のP(式1)やP(式2)についても繰り返し同様な変形を行っていき，最終的に関数Pで変換できるものが無くなった時に，中置記法から後置記法へと完全に変換できたということになる．具体例と共に変換の様子を見ていく．例えば中置記法で(ab)+(cd)という式の場合

P((a*b)+(c*d))
=P(a*b)P(c*d)+
=P(a)P(b)*P(c)P(d)*+
=ab*cd*+

と変換される．

2.2 スタック

スタックは積み重ねという意味である．コンパイラの中ではスタックが様々な場面で使われる．スタックとは後に入れたものほど先に取り出す(Last-In First-Out)の方法をとる．棚に物を積んでそれを降ろすときの様に後から積んだものが先に降ろされるので，棚と呼ばれることもある．

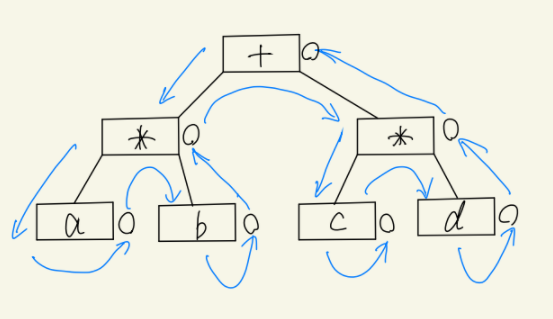
木構造で表された式を後置記法に変換する方法について説明する．下の図は式ab+cdを木構造で表したものである．この木構造を下図の青い矢印のようにたどる際に，根は3回目の訪問で出力，葉は2回目の訪問で出力，すると後置記法が得られる．図の丸で書かれた部分が出力するタイミングとなる．これによりabcd+という後置記法が得られる．

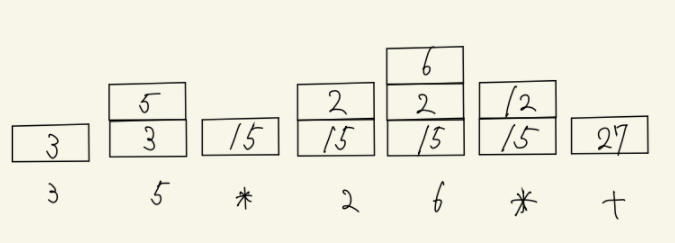
さらに，後置記法の式をスタックを用いて計算することが出来る．下図の四角はスタックを意味している．四角の下の数字や記号は，スタックにその数字や記号を入れようとしていることを意味する．スタックに入れようとしている記号が演算子である場合，その時点でスタックに積まれている上から2つの演算数をスタックから取り出し，演算子によって計算したものをスタックの一番上に積む．下図の左から3番目のブロックの例ではスタックに3,5が積まれている状態で，次に「*」を読み込んだ際に，35から計算される数字15をスタックに積むことになる．また，スタックに入れようとしている記号が演算数の場合は，そのままスタックに積む．下図は中置記法で35+26,後置記法で3526*+と表される式を，スタックを用いて計算するときの流れを示している．

さらに，中置記法の式を後置記法に変換する際にもスタックが用いられる．その時のアルゴリズムは以下の通り．
(1) 一番最初にスタックに左括弧を積む．
(2)演算数を読んだらそれをそのまま出力する．
(3)演算子を読んだら，スタックの上にそれより優先順位の高い演算子があればあるだけそれをスタックから降ろして出力し，読んだ演算子をスタックに積む．ただし，式の終わりになったら，右括弧（どの演算子よりも優先順位の低い演算子)を読んだことにする．

演算子の優先順位は以下の通り．同じ優先順位年の演算子を比較する際には後置記法上で左側にあるほど優先順位が高いものとする．

*=/ > +=- > ( > )

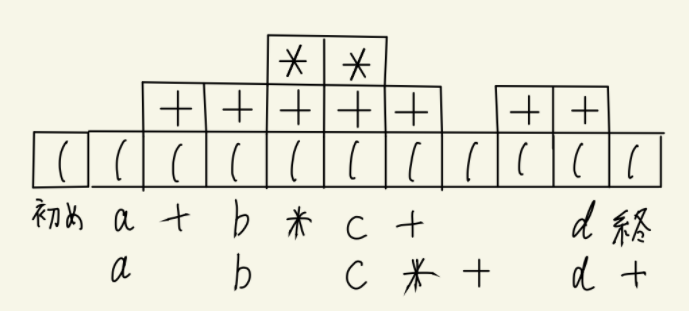
下図は，中置記法の式a+b*c+dを，後置記法に変換するときのスタックの様子を表している．ブロックの下で１行目の文字列は記号の入力を表し，2行目は出力を表している．

2.3 簡単なコンパイラの例

変数abcに値を代入する文を，2.2で説明したスタックを用いた読み込み方を使って処理する．

abc := e3 * 2.56 + abc / e3;

変数名表（１）

番号	変数名	種類	値
0	abc	real	100
1	e3	real	104
2	fg	real	108

基本的には，2.2で説明した中置記法から後置記法に変換する方法を行っていく．まず最初に変数abcを読み込む．変数abcは変数名表1の第0番目の行にあるため，(1,0)を出力する．

出力結果

(1,0)

次に「:=」の代入記号を読み込む．これを(8,1)という記号(8は演算記号，1は代入を意味する演算記号)としてスタックに積む．この時のスタックは以下の通り．最初に左括弧をスタックに積んだ状態で，今回の「:=」を表す1が積まれている．

(	1
次に同様にして，「e3」を読んで(1,1)を出力する．これは変数名表１の１番目を意味している．さらに，「*」を読んで(8,5)という記号にしてスタックに積む．この時，「*」の演算子の順位が5であり，すでにスタックに積まれている1よりも高くないため，そのままスタックに積まれたのである．

出力結果

(1,0)(1,1)

(	1	5
次に定数「2.56」を調べたところで，それを定数表２に書き込み,さらに定数表2の0番目を意味する(2,0)を出力する．

定数表（２）

番号	値	種類	番地
0	2.56	real	200

出力結果

(1,0)(1,1)(2,0)

次に「+」を読み込む．これは既にすでにスタックに積まれている5よりも優先順位の低いものであるため，(8,5)を出力して，スタックに３(+)を積む．

(	1	3
次の「abc」は(1,0)として出力する．次の「/」記号(8,6)の優先順位は3(+)より高いため，スタックに積む．

(	1	3	6

出力結果

(1,0)(1,1)(2,0)(8,5)

最後に「e3」を読んで(1,1)を出力し，「;」を読んでスタックに積まれた記号を6, 3, 1, の順に降ろして出力する．

出力結果

(1,0)(1,1)(2,0)(8,5)(1,0)(1,1)(8,6)(8,3)(8,1)

この最終的な出力結果によって以下の後置記法が得られる．

abc e3 2.56 * abc e3 / + :=

2.4 コンパイラの論理的構造

読み込まれた原子プログラムの文字列を1字1句調べながら，プログラム言語の要素を切り出していく作業が必要となる．その際に，文字列が定数であるのか，変数名であるのか，演算子であるのかなどの解析が行われる．これを字句解析という．