Codeforces Rond #739 (Div. 3) 解いた感想

A. Dislike of Threes

考えたこと

3で割り切れる整数と一の位が3の数を除いて，それ以外の整数を配列に入れました．配列の一番最初に適当な数を入れておくと，添え字とkが一致します．

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i,n) for(ll i=0; i<(n); i++)

int main() {
    int t; cin >> t;
    vector<ll> v;
    v.push_back(0);
    for(ll i=1; i<=100000; i++){
        if(i%3 == 0 || i%10 == 3) continue;
        v.push_back(i);
    }
    rep(i,t){
        ll k; cin >> k;
        cout << v[k] << endl;
    }
    
    return 0;
}

B. Who's Opposite?

https://codeforces.com/contest/1560/problem/B?locale=en

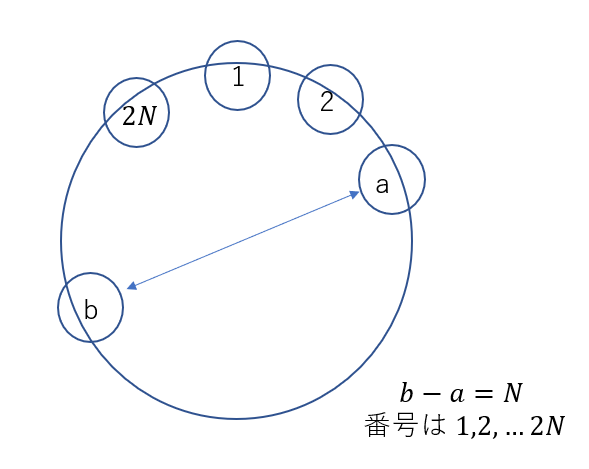
$c \leq N$ のとき，答えは$c+N$
$c>N$のとき，答えは$c-N$
答えが存在するための条件は，$1\leq a, b, c \leq 2N$

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i,n) for(ll i=0; i<(n); i++)

int main() {
    ll t; cin >> t;
    rep(i,t){
        ll a, b, c;
        cin >> a >> b >> c;
        ll n = abs(a-b);
        if(a>2*n || b>2*n || c>2*n) cout << -1 << endl;
        else if(c<=n) cout << c+n << endl;
        else cout << c-n << endl;
    }
    return 0;
}

C. Infinity Table

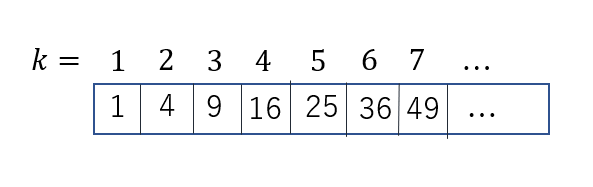
数字の配置は下の図のようになっています．バームクーヘンの層みたいに考えたとときに，与えられた数字が最初から何番目の層なのか？を変数$k$を使って表しています．この$k$を二分探索を用いて予め求めておきます．下図の2つ目のような，（添え字番号）＾２の配列を用意して，lower_boundを使って求めます．kが求まったら，入力された数字から$(k-1)^2$を引くと，層の中でその数字が何番目に位置しているかが分かります．その後は，頑張って答えを出します．

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i,n) for(ll i=0; i<(n); i++)
#define all(x) (x).begin(), (x).end()
#define lb(c, x) distance((c).begin(), lower_bound(all(c), (x)))

int main() {
    ll t; cin >> t;
    vector<ll> v;
    for(ll i=0; ; i++){
        if(i*i>1000000000) break;
        v.push_back(i*i);
    }
    rep(i,t){
        ll n; cin >> n;
        ll k = lb(v, n);
        ll sum = k*k-(k-1)*(k-1), h = n-(k-1)*(k-1);
        ll I, J;
        if(h<=(sum+1)/2){
            I = h;
            J = k;
        }else{
            I = k;
            J = k-(h-sum/2)+1;
        }
        cout << I << " " << J << endl;

    } 
    return 0;
}