LoginSignup
1
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@fred55

ブースティングアルゴリズムを実装してみた

Posted at

はじめに

  • ブースティングアルゴリズムを理解するためにシンプルなバージョンを実装してみた。

AdaBoostのアルゴリズム

説明変数$x_i(i=1,\dots,N)$を用いて2値の目的変数$y_i(=\pm1)$を予測する。
弱学習器$k_m(x_i)$の予測値を係数$\beta_m(m=1,2,\dots)$で順番に加算して新しい学習器$f_m(x_i)$を作る。
$f_m(x_i)$の符号を予測値とする。損失関数を$E=\sum_i\exp(-y_if_m(x_i))\ $として、
これを最小化するように新しく追加する$k_m(x_i)$と$\beta_m$を決定する。

\begin{align}
f_m(x_i)&=\beta_1k_1(x_i)+\cdots+\beta_mk_m(x_i)\\
f_m(x_i)&=f_{m-1}(x_i)+\beta_m k_m(x_i),\quad w^{(m)}_i=\exp(-y_if_{m-1}(x_i))\\
E&=\sum_{i=1}^N\exp(-y_if_m(x_i))=\sum_{i=1}^Nw^{(m)}_i\exp(-y_i\beta_mk_m(x_i))\\
&=\sum_{y_i=k_m(x_i)}w^{(m)}_i\exp(-\beta_m)+\sum_{y_i\neq k_m(x_i)}w^{(m)}_i\exp(\beta_m)\\
&=\sum_{i=1}^Nw^{(m)}_i\exp(-\beta_m)+\sum_{y_i\neq k_m(x_i)}w^{(m)}_i(\exp(\beta_m)-\exp(-\beta_m))\ 
\end{align}

従って誤分類する重み$w^{(m)}_i$の合計を最小化するように$k_m(x_i)$を構成すれば$E$が最小となる。
係数$\beta_m$は$E$を最小化する条件から求められる。

\begin{align}
\frac{dE}{d\beta_m}&=-\sum_{y_i=k_m(x_i)}w^{(m)}_i\exp(-\beta_m)+\sum_{y_i\neq k_m(x_i)}w^{(m)}_i\exp(\beta_m)=0\ \\
\beta_m&=\frac{1}{2}\log\frac{\sum_{y_i=k_m(x_i)}w^{(m)}_i}{\sum_{y_i\neq k_m(x_i)}w^{(m)}_i}\\
&=\frac{1}{2}\log\frac{1-\epsilon_m}{\epsilon_m},\quad
\epsilon_m=\frac{\sum_{y_i\neq k_m(x_i)}w^{(m)}_i}{\sum w^{(m)}_i}\\
w^{(m+1)}_i&=w^{(m)}_i\exp(-y_i\beta_mk_m(x_i))
\end{align}

$w^{(1)}_i=1$から開始して、$k_m(x_i)(m=1,2,\dots)$を構成しながら、係数$\beta_m$で加算していく。

サンプルデータ

$x_i$として10次元の標準正規分布を使用。
トレーニングデータを2000件、テストデータを1000件作成。
原点までの距離で半分に分けて、遠い方を$y_i=1$、近い方を$y_i=-1\ $とする。

set.seed(10)
d = 10
n_train = 2000
R2 = qchisq(p=0.5, df=d)
x_train = matrix(rnorm(n_train*d), nrow=n_train, ncol=d)
y_train = ifelse(rowSums(x_train^2) > R2, 1, -1)
n_test = 1000
x_test = matrix(rnorm(n_test*d), nrow=n_test, ncol=d)
y_test = ifelse(rowSums(x_test^2) > R2, 1, -1)

AdaBoostの実装

説明変数を一つ選択して二つに分割する単純な切株モデルを弱学習器として使用。
重複する値を分割の候補から除外するためにduplicated()を使用している。

# 誤分類する重みの合計を最小化する切株モデル
sstump = function(x, y, weight=NULL) {
  if(is.null(weight)){weight = rep(1, nrow(x))}
  splits = lapply(sample.int(ncol(x)), function(i) {
    t = order(x[, i])
    xt = x[t, i]
    yt = y[t]
    wt = weight[t]
    wt_left_a = cumsum(ifelse(yt == -1, wt, 0))
    wt_left_b = cumsum(ifelse(yt == 1, wt, 0))
    wt_right_a = sum(wt[yt == -1]) - wt_left_a
    wt_right_b = sum(wt[yt == 1]) - wt_left_b
    error = pmin(wt_left_a, wt_left_b) + pmin(wt_right_a, wt_right_b)
    error[duplicated(xt, fromLast=T)] = Inf
    k = which.min(error)
    list(index = i,
         error = error[k],
         split = xt[k],
         left  = ifelse(wt_left_a[k] >= wt_left_b[k], -1, 1),
         right = ifelse(wt_right_a[k] >= wt_right_b[k], -1, 1))
  })
  model = Reduce(function(x, y){if(x$error <= y$error){x}else{y}}, splits)
  class(model) = "sstump"
  model
}
predict.sstump = function(model, x) {
  ifelse(x[, model$index] <= model$split, model$left, model$right)
}

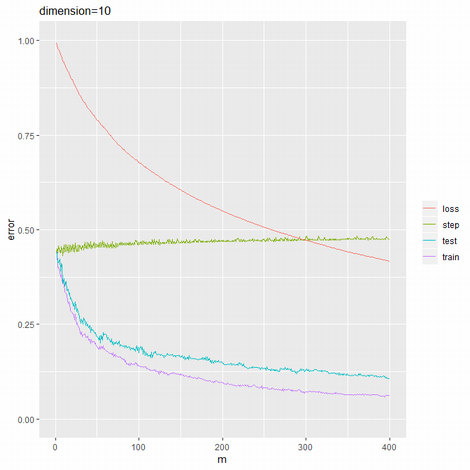
AdaBoostの実行結果

400回実行。重みを合計したものが損失関数の値となる。

set.seed(10)
M = 400
beta = 0
weight = rep(1, n_train)
f_train = rep(0, n_train)
f_test = rep(0, n_test)
step_err = 0
loss = 0
train_err = 0
test_err = 0
for (m in 1:M) {
  model = sstump(x_train, y_train, weight)
  y_pred = predict(model, x_train)
  step_err[m] = sum(weight[y_train != y_pred]) / sum(weight)
  beta[m] = log((1 - step_err[m]) / step_err[m]) / 2
  weight = weight * exp(-y_train * y_pred * beta[m])
  loss[m] = mean(weight)
  f_train = f_train + beta[m] * y_pred
  ada_train = ifelse(f_train > 0, 1, -1)
  train_err[m] = mean(y_train != ada_train)
  f_test = f_test + beta[m] * predict(model, x_test)
  ada_test = ifelse(f_test > 0, 1, -1)
  test_err[m] = mean(y_test != ada_test)
}

ggplotでグラフを作成。

library(ggplot2)

df_ada = data.frame(m=seq_along(test_err),train=train_err,test=test_err,
  step=step_err,beta=beta,loss=loss)
rbind(head(df_ada),tail(df_ada))

ggplot(df_ada, aes(x=m)) +
  geom_line(aes(y=train,color="train")) +
  geom_line(aes(y=test,color="test")) +
  geom_line(aes(y=step,color="step")) +
  geom_line(aes(y=loss,color="loss")) +
  scale_color_discrete(name=NULL) +
  labs(title=paste("dimension",d,sep='='),y="error")

      m  train  test      step       beta      loss
1     1 0.4405 0.439 0.4405000 0.11956654 0.9928943
2     2 0.4405 0.439 0.4502647 0.09980063 0.9879700
3     3 0.4010 0.414 0.4383692 0.12389155 0.9804360
4     4 0.4010 0.414 0.4582858 0.08362284 0.9770179
5     5 0.3890 0.422 0.4427193 0.11506647 0.9705854
6     6 0.3755 0.391 0.4397072 0.12117517 0.9635030
395 395 0.0630 0.108 0.4745115 0.05102122 0.4194590
396 396 0.0630 0.110 0.4821049 0.03580547 0.4191902
397 397 0.0625 0.107 0.4795388 0.04094520 0.4188391
398 398 0.0630 0.108 0.4775253 0.04497972 0.4184157
399 399 0.0630 0.107 0.4744743 0.05109586 0.4178701
400 400 0.0630 0.107 0.4758289 0.04837990 0.4173816

ada_boost.png

単体の切株モデルでは予測誤差率44%だったものが、合算することで11%まで改善している。

Gradient Tree Boostingのアルゴリズム

2値の目的変数$y(=\pm1)$に対してベルヌーイ分布を仮定して対数オッズ$F$を予測する。
負の対数尤度を$L(y,F)$とする。

\begin{align}
\Pr(y=1)&=p=\frac{1}{1+\exp(-F)},\quad F=\log\frac{p}{1-p}\\
L(y,F)&=-\frac{1+y}{2}\log p-\frac{1-y}{2}\log(1-p)\\
&=\frac{1+y}{2}\log(1+\exp(-F))+\frac{1-y}{2}\log(1+\exp(F))\\
&=\log(1+\exp(-yF))\\
\frac{d L}{d F}&=\frac{-y\exp(-yF)}{1+\exp(-yF)}
=\frac{-y}{1+\exp(yF)}=p-\frac{1+y}{2}\\
\frac{d^2 L}{d F^2}&=\frac{y^2\exp(yF)}{(1+\exp(yF))^2}=p(1-p)
\end{align}

$L$の合計を最小化する値を$F$の初期値とする。

\begin{align}
L(F)&=\sum_iL(y_i,F)=\sum_i\log(1+\exp(-y_iF))\\
\frac{d L}{d F}&=\sum_i\frac{-y_i}{1+\exp(y_iF)}
=\sum_{y_i=1}\frac{-1}{1+\exp(F)}+\sum_{y_i=-1}\frac{1}{1+\exp(-F)}=0\\
F^{(0)}&=\log\frac{\sum_{y_i=1}1}{\sum_{y_i=-1}1}
\end{align}

$L$の合計を最小化するようにケース$i$の推定値$F^{(t)}_i(t=0,\dots)$を逐次的に更新していく。
決定木を用いてリーフ$j(1,\dots,T)\ $にケース$i\in I_j$をまとめて、$L$を最小化するリーフの更新値$f_j$を求める。
$L$の差分をテイラー展開して二次の項までの近似を行なうことにより$f_j$の推定値を求める。

\begin{align}
F^{(t+1)}_i&=F^{(t)}_i+f_j\quad(i\in I_j,j=1,\dots,T)\\
L^{(t)}&=\sum_{j=1}^T\sum_{i\in I_j}\log(1+\exp(-y_iF^{(t)}_i))\\
\Delta L^{(t)}&\simeq\sum_{j=1}^T\sum_{i\in I_j} \left(g_i f_j+\frac{1}{2}h_i f_j^2\right)\\
g_i&=p_i-\frac{1+y_i}{2},h_i=p_i(1-p_i),p_i=\frac{1}{1+\exp(-F^{(t)}_i)}\\
\hat{f}_j&=-\frac{\sum g_i}{\sum h_i},\quad
\Delta\hat{L}^{(t)}_j=-\frac{1}{2}\frac{(\sum g_i)^2}{\sum h_i}
\end{align}

$\Delta\hat{L}^{(t)}_j\ $の合計を最小化するように決定木を構成して、$F^{(t)}_i$に$\hat{f}_j$を加算する。

Gradient Tree Boostingの実装

説明変数を一つ選択して二つに分割する単純な切株モデルを弱学習器として使用。
一次と二次の勾配情報gr,hsからscore=$-2\Delta L$を最大化する分割を求める。

# スコアを最大化する切株モデル
sstump_gtb = function(x, gr, hs) {
  splits = lapply(sample.int(ncol(x)), function(i) {
    t = order(x[, i])
    xt = x[t, i]
    gt = gr[t]
    ht = hs[t]
    gt_left = cumsum(gt)
    gt_right = sum(gt) - gt_left
    ht_left = cumsum(ht)
    ht_right = sum(ht) - ht_left
    ht_right[length(ht_right)] = 1 # avoid zero division
    score = gt_left * gt_left / ht_left + gt_right * gt_right / ht_right
    score[duplicated(xt, fromLast=T)] = -Inf
    k = which.max(score)
    list(index = i,
         score = score[k],
         split = xt[k],
         left  = -gt_left[k] / ht_left[k],
         right = -gt_right[k] / ht_right[k])
  })
  model = Reduce(function(x, y){if(x$score >= y$score){x}else{y}}, splits)
  class(model) = "sstump_gtb"
  model
}
predict.sstump_gtb = function(model, x){
  ifelse(x[, model$index] <= model$split, model$left, model$right)
}

Gradient Tree Boostingの実行結果

set.seed(10)
M = 400
models = list()
f0 = log(sum(y_train == 1) / sum(y_train == -1))
f_train = rep(f0, n_train)
f_test = rep(f0, n_test)
train_err = 0
test_err = 0
loss = 0
for (m in 1:M) {
  prob = 1 / (1 + exp(-f_train))
  gr = prob - (1 + y_train) / 2
  hs = prob * (1 - prob)
  model = sstump_gtb(x_train, gr, hs)
  models = append(models, list(model))
  f_train = f_train + predict(model, x_train)
  y_pred = ifelse(f_train > 0, 1, -1)
  train_err[m] = mean(y_train != y_pred)
  loss[m] = mean(log(1 + exp(-y_train * f_train)))
  f_test = f_test + predict(model, x_test)
  y_pred = ifelse(f_test > 0, 1, -1)
  test_err[m] = mean(y_test != y_pred)
}

ggplotでグラフを作成。

df_gtb = data.frame(m=seq_along(test_err),train=train_err,test=test_err,loss=loss)
rbind(head(df_gtb),tail(df_gtb))

ggplot(df_gtb, aes(x=m)) +
  geom_line(aes(y=train,color="train")) +
  geom_line(aes(y=test,color="test")) +
  geom_line(aes(y=loss,color="loss")) +
  scale_color_discrete(name=NULL) +
  labs(title=paste("dimension",d,sep='='),y="error")

      m  train  test       loss
1     1 0.4530 0.449 0.67517890
2     2 0.4120 0.417 0.65801367
3     3 0.3785 0.381 0.64112428
4     4 0.3460 0.348 0.62493165
5     5 0.3220 0.326 0.60779420
6     6 0.3025 0.312 0.59134871
395 395 0.0005 0.062 0.02579554
396 396 0.0005 0.059 0.02571115
397 397 0.0000 0.062 0.02562471
398 398 0.0000 0.062 0.02551885
399 399 0.0000 0.062 0.02541327
400 400 0.0000 0.061 0.02530959

gtb.png

AdaBoostの予測誤差率11%を上回る6%を達成。収束が速い。

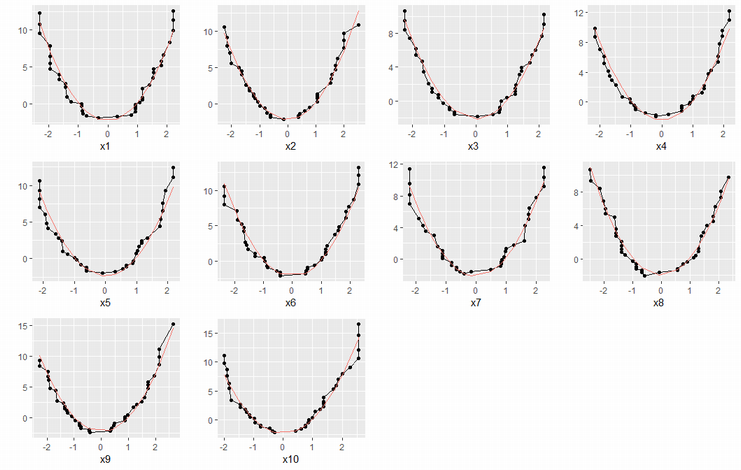
予測値は、切株モデルにより互いに独立な関数の和に分解される。
$F(x_i)=g_1(x_{i1})+\dots+g_d(x_{id})$
サンプルデータの特性から、$g(x)=(x^2-R_2/d)c\ $と表現されるように思われる。
説明変数毎の予測値をグラフにしてみた。

library(gridExtra)

df_model = t(sapply(models,function(x){c(index=x$index,split=x$split,left=x$left,right=x$right)}))
df_model = as.data.frame(df_model)

g_list = lapply(1:d, function(i) {
  df_model_x = df_model[df_model$index==i,]
  df_model_x = df_model_x[order(df_model_x$split),]
  df_model_x$f = sum(df_model_x$left) - cumsum(df_model_x$left) + cumsum(df_model_x$right)
  pred = df_model_x$split^2 - R2 / d
  coef = sum(df_model_x$f * pred) / sum(pred^2)
  df_model_x$pred = pred * coef
  ggplot(df_model_x, aes(x=split, y=f)) +
    geom_line() + geom_point() +
    geom_line(aes(y=pred, color="pred")) +
    labs(x=paste("x", i, sep=''), y="") +
    theme(legend.position="none")
})

grid.arrange(grobs=g_list, nrow=3, ncol=4)

gtb_x.png

おわりに

  • AdaBoostは、弱学習器の予測結果を合算することで高精度のモデルを構築する。
  • Gradient Tree Boostingは、損失関数を弱学習器で最小化することにより高精度のモデルを構築する。
  • AdaBoostが使用している損失関数に適用することも可能。オリジナルよりも速く収束する。

参考情報

1
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?