半導体ウェハー生産計画の最適化

#はじめに

• CPLEX CP Optimizerの資料で説明されている半導体ウエハー生産計画の最適化を再現してみた。
• https://www.slideshare.net/PhilippeLaborie/introduction-to-cp-optimizer-for-scheduling
• https://ibmdecisionoptimization.github.io/docplex-doc/cp/index.html

#生産計画の仕様

• ロットは、ウエハーの数(n)、優先度(priority)、生産開始可能日(release_date)、納期(due_date)を持つ。
• ロット毎に、生産ステップのシーケンスが与えられる。
• ロットを構成するステップの間隔(lag)が長くなるとコストが発生する。
• 各ステップはファミリー(f)を持つ。
• ファミリーに対して、生産可能なマシンと生産時間(process_time)が与えられる。
• ファミリーが同じステップは同時に生産することができる。開始と終了は同じとなる。
• 生産するステップのファミリーを切替えるには一定の時間が掛かる。
• マシンはキャパシティ(capacity)を持つ。同時に生産できるウエハー数の上限値。
• 最小化する指標は、ステップ間隔コスト$V_1$と納期遅れコスト$V_2$の二つ。

\begin{align*}
V_1&=\sum_{\mathrm{Step}} \min(c,c\max(0,\mathrm{lag}-a)^2/(b-a)^2)\\
V_2&=\sum_{\mathrm{Lot}} p\max(0,\mathrm{EndOfLot}-\mathrm{DueDate})
\end{align*}

• ロット数: 1000
• ステップ数: 5000
• マシン数: 150
• 各ステップが生産可能なマシン数: 10
• 生産計画の期間は48時間で分単位

#CP Optimizerによる実装

• プログラミング言語はOPL。CPLEX Optimization Studioで実行。
• 50行でExcellent Performanceが得られるとのこと。
• 変数名を長めに変更。

using CP;
tuple Lot { key int id; int n; float priority; int release_date; int due_date; }
tuple LotStep { key Lot lot; key int pos; int f; }
tuple Lag { Lot lot; int pos1; int pos2; int a; int b; float c; }
tuple Machine { key int id; int capacity; }
tuple MachineFamily { Machine machine; int f; int process_time; }
tuple MachineStep { Machine machine; LotStep lot_step; int process_time; }
tuple Setup { int f1; int f2; int duration; }

{Lot} Lots = ...;
{LotStep} LotSteps = ...;
{Lag} Lags = ...;
{Machine} Machines = ...;
{MachineFamily} MachineFamilies = ...;
{Setup} MachineSetups[machine in Machines] = ...;

{MachineStep} MachineSteps = {<machine_family.machine,lot_step,machine_family.process_time>
  | lot_step in LotSteps, machine_family in MachineFamilies: machine_family.f==lot_step.f};

dvar interval d_lot[lot in Lots] in lot.release_date .. 48*60;
dvar interval d_lot_step[lot_step in LotSteps];
dvar interval d_machine_step[ms in MachineSteps] optional size ms.process_time;

dvar int d_lag[Lags];

stateFunction batch[machine in Machines] with MachineSetups[machine];
cumulFunction load [machine in Machines] = 
  sum(ms in MachineSteps: ms.machine==machine) pulse(d_machine_step[ms], ms.lot_step.lot.n);

minimize staticLex(
  sum(lag in Lags) minl(lag.c, lag.c * maxl(0, d_lag[lag]-lag.a)^2 / (lag.b-lag.a)^2),
  sum(lot in Lots) lot.priority * maxl(0, endOf(d_lot[lot]) - lot.due_date));
subject to {
  forall(lot in Lots)
    span(d_lot[lot], all(lot_step in LotSteps: lot_step.lot==lot) d_lot_step[lot_step]);
  forall(lot_step in LotSteps) {
    alternative(d_lot_step[lot_step], all(ms in MachineSteps: ms.lot_step==lot_step) d_machine_step[ms]);
    if (lot_step.pos > 1)
      endBeforeStart(d_lot_step[<lot_step.lot,lot_step.pos-1>],d_lot_step[lot_step]);
  }
  forall(ms in MachineSteps)
    alwaysEqual(batch[ms.machine], d_machine_step[ms], ms.lot_step.f, true, true);
  forall(machine in Machines)
    load[machine] <= machine.capacity;
  forall(lag in Lags)
    endAtStart(d_lot_step[<lag.lot,lag.pos1>], d_lot_step[<lag.lot,lag.pos2>], d_lag[lag]);
}

#サンプルデータの作成

乱数を使用してサンプルデータを作成。
alphaは生産開可能なマシンの比率。

from dataclasses import dataclass, field
import docplex.cp.model as cp
from docplex.cp.expression import CpoIntervalVar
import random
import pandas as pd
import numpy as np

@dataclass
class lot_type:
    id: int
    n: int
    priority: float
    release_date: int
    due_date: int
    step_list: list

@dataclass
class step_type:
    id: int
    family: int
    a: float
    b: float
    c: float
    start: int = field(init=False, default=0)
    end: int = field(init=False, default=0)
    machine_id: int = field(init=False, default=0)

@dataclass
class machine_type:
    id: int
    capacity: int
    setup_list: list
    proc_time: dict = field(init=False, default_factory=dict)
    job_list: list = field(init=False, default_factory=list)

@dataclass
class setup_type:
    family1: int
    family2: int
    duration: int

@dataclass
class job_type:
    n: int
    family: int
    interval_var: CpoIntervalVar
    start: int = field(init=False, default=0)
    end: int = field(init=False, default=0)

random.seed(5)

n_lot, n_step, n_family, n_machine = 4, 5, 3, 4
lot_n = (5, 15)
capa = (20, 60)
proc_time = (20, 30)
takt, LT = 30, 100
a, b, c = 10, 20, 5
alpha = 0.5
duration = 20

lot_list = []
for l in range(n_lot):
    n = random.randint(lot_n[0], lot_n[1])
    p = random.randint(1, 10) / 10
    step_list = [step_type(s, random.randint(0, n_family-1), a, b, c) for s in range(n_step)]
    lot = lot_type(l, n, p, takt*l, takt*l+LT, step_list)
    lot_list.append(lot)

machine_list = []
for m in range(n_machine):
    setup_list = []
    for j in range(n_family):
        for k in range(n_family):
            setup_list.append(setup_type(j, k, 0 if j == k else duration))
    c = random.randint(capa[0], capa[1])
    machine = machine_type(m, c, setup_list)
    machine_list.append(machine)

for f in range(n_family):
    cnt = 0
    for m in range(n_machine):
        if random.random() > alpha: continue
        machine_list[m].proc_time[f] = random.randint(proc_time[0], proc_time[1])
        cnt += 1
    if cnt == 0:
        m = random.randint(0, n_machine-1)
        machine_list[m].proc_time[f] = random.randint(proc_time[0], proc_time[1])

#CPLEX Optimization Studio用データの作成

path_file_name = 'sample.dat'
def mytuple(obj):
    if type(obj) == lot_type:
        return f'<{obj.id},{obj.n},{obj.priority},{obj.release_date},{obj.due_date}>'
    if type(obj) == machine_type:
        return f'<{obj.id},{obj.capacity}>'

with open(path_file_name, 'w') as o:
    o.write('Lots = {\n')
    for lot in lot_list:
        o.write(f'  {mytuple(lot)}\n')
    o.write('};\n')
    o.write('LotSteps = {\n')
    for lot in lot_list:
        for s, step in enumerate(lot.step_list):
            o.write(f'  <{mytuple(lot)},{s+1},{step.family}>\n')
    o.write('};\n')
    o.write('Lags = {\n')
    for lot in lot_list:
        for l in range(len(lot.step_list)-1):
            step = step_list[s]
            o.write(f'  <{mytuple(lot)},{l+1},{l+2},{step.a},{step.b},{step.c}>\n')
    o.write('};\n')
    o.write('Machines = {\n')
    for machine in machine_list:
        o.write(f'  {mytuple(machine)}\n')
    o.write('};\n')
    o.write('MachineFamilies = {\n')
    for machine in machine_list:
        for f, proc_time in machine.proc_time.items():
            o.write(f'  <{mytuple(machine)},{f},{proc_time}>\n')
    o.write('};\n')
    o.write('MachineSetups = #[\n')
    for machine in machine_list:
        o.write(f'  <{machine.id}>:{{')
        for setup in machine.setup_list:
            o.write(f'<{setup.family1},{setup.family2},{setup.duration}>')
        o.write('}\n')
    o.write(']#;\n')

#Python Libraryによる実装

サンプルデータの作成で使用したオブジェクトをそのまま流用。
モデルの作成と最適化、結果出力。

model = cp.CpoModel()
interval_name_to_step = {}
for lot in lot_list:
    lot.interval_var = cp.interval_var(start=[lot.release_date,48*60], end=[lot.release_date,48*60], name=f'I{lot.id}')
    for s, step in enumerate(lot.step_list):
        step.interval_var = cp.interval_var(name=f'I{lot.id}_{s}')
        interval_list = []
        for machine in machine_list:
            if step.family not in machine.proc_time: continue
            name = f'I{lot.id}_{s}_{machine.id}'
            interval_var = cp.interval_var(length=machine.proc_time[step.family], optional=True, name=name)
            interval_list.append(interval_var)
            machine.job_list.append(job_type(lot.n, step.family, interval_var))
            interval_name_to_step[interval_var.name] = step
        model.add(cp.alternative(step.interval_var, interval_list))
    model.add(cp.span(lot.interval_var, [step.interval_var for step in lot.step_list]))
    for s in range(len(lot.step_list)-1):
        lot.step_list[s].int_var = cp.integer_var(min=0, max=48*60, name=f'A{lot.id}_{s}')
        model.add(cp.end_at_start(lot.step_list[s].interval_var, lot.step_list[s+1].interval_var, lot.step_list[s].int_var))

for machine in machine_list:
    tmat = cp.transition_matrix(n_family)
    for setup in machine.setup_list:
        tmat.set_value(setup.family1, setup.family2, setup.duration)
    state = cp.state_function(tmat, name=f'S{machine.id}')
    pulse_list = []
    for job in machine.job_list:
        model.add(cp.always_equal(state, job.interval_var, job.family, True, True))
        pulse_list.append(cp.pulse(job.interval_var, job.n))
    model.add(cp.sum(pulse_list) <= machine.capacity)

lag_list = []
for lot in lot_list:
    for s in range(len(lot.step_list)-1):
        step = lot.step_list[s]
        lag_list.append(cp.min(step.c, step.c * cp.square(cp.max(0, step.int_var - step.a)) / (step.b - step.a)**2))
obj_lag = cp.sum(lag_list)
obj_lot = cp.sum([lot.priority * cp.max(0, cp.end_of(lot.interval_var) - lot.due_date) for lot in lot_list])
model.add(cp.minimize_static_lex([obj_lag, obj_lot]))

msol = model.solve(LogVerbosity='Terse', Workers=2, NoOverlapInferenceLevel='Medium', RandomSeed=1)
print(msol.get_search_status(), msol.get_objective_values())

#最適化結果の出力

for machine in machine_list:
    for job in machine.job_list:
        x = msol.get_value(job.interval_var)
        if(len(x) == 0):
            job.n = 0
            continue
        job.start = x[0]
        job.end = x[1]
        step = interval_name_to_step[job.interval_var.name]
        step.start = job.start
        step.end = job.end
        step.machine_id = machine.id

result = []
for lot in lot_list:
    for step in lot.step_list:
        result.append([lot.id, lot.n, lot.priority, lot.release_date, lot.due_date,
                       step.id, step.family, step.start, step.end, (step.end-step.start),
                       step.machine_id, machine_list[step.machine_id].capacity])
result = pd.DataFrame(result, columns=['lot', 'n', 'priority', 'release_date', 'due_date',
                                       'step', 'family', 'start', 'end', 'size',
                                       'machine', 'capacity'])
result.sort_values(['lot', 'start'], inplace=True, ignore_index=True)
result.to_csv('semi_cplex.csv', index=False)

#実行結果

最適解が得られた。計算時間は0.1秒程度。
CP OptimizerでもPythonでも同一の結果となった。

l	n	priority	release_date	due_date	pos	f	start	end	length	m	capacity
0	14	0.5	0	100	0	2	0	23	23	1	44
0	14	0.5	0	100	1	1	30	53	23	2	30
0	14	0.5	0	100	2	2	53	76	23	1	44
0	14	0.5	0	100	3	2	76	99	23	1	44
0	14	0.5	0	100	4	2	99	122	23	1	44
1	13	0.1	30	130	0	1	30	53	23	2	30
1	13	0.1	30	130	1	0	53	76	23	3	24
1	13	0.1	30	130	2	2	76	99	23	1	44
1	13	0.1	30	130	3	0	99	128	29	0	31
1	13	0.1	30	130	4	0	128	151	23	3	24
2	6	0.6	60	160	0	1	60	83	23	2	30
2	6	0.6	60	160	1	0	83	106	23	3	24
2	6	0.6	60	160	2	1	106	129	23	2	30
2	6	0.6	60	160	3	2	129	152	23	1	44
2	6	0.6	60	160	4	0	152	172	20	2	30
3	14	0.4	90	190	0	0	99	128	29	0	31
3	14	0.4	90	190	1	2	129	152	23	1	44
3	14	0.4	90	190	2	0	152	172	20	2	30
3	14	0.4	90	190	3	1	172	194	22	1	44
3	14	0.4	90	190	4	1	194	216	22	1	44

#ガントチャートの出力

import matplotlib
import matplotlib.pyplot as plt
from matplotlib import gridspec

area_w = max([step.end for lot in lot_list for step in lot.step_list])
lot_h = np.array([lot.n for lot in lot_list])
area_lot_h = sum(lot_h)
machine_h = np.array([machine.capacity for machine in machine_list])
area_machine_h = sum(machine_h)

for machine in machine_list:
    machine.job_list.sort(key=lambda job: job.start)
    i = 0
    j = 1
    while i < len(machine.job_list) and j < len(machine.job_list):
        job_i = machine.job_list[i]
        job_j = machine.job_list[j]
        if job_i.n == 0 or job_i.start < job_j.start:
            i = j
            j = j+1
            continue
        if job_j.n == 0:
            j = j+1
            continue
        job_i.n += job_j.n
        job_j.n = 0
        j = j+1

lot_y = np.cumsum(lot_h) - lot_h
def lot_generator():
    for lot in lot_list:
        for step in lot.step_list:
            yield (step.start, lot_y[lot.id], (step.end-step.start), lot.n, step.family, f'{step.machine_id}-{step.family}')

machine_y = np.cumsum(machine_h) - machine_h
def machine_generator():
    for machine in machine_list:
        for job in machine.job_list:
            if job.n == 0: continue
            yield (job.start, machine_y[machine.id], (job.end-job.start), job.n, job.family, f'{machine.id}-{job.family}')

my_rect = matplotlib.patches.Rectangle
cmap = plt.cm.get_cmap('hsv', n_family+1)
fig = plt.figure(figsize=(12, 8))
spec = gridspec.GridSpec(ncols=1, nrows=2, height_ratios=[area_lot_h, area_machine_h])

def draw_box(ax, box_generator):
    for (x,y,w,h,f,lab) in box_generator():
        rectangle = my_rect((x, y), w, h, fill=False, color=cmap(f), hatch='/')
        ax.add_patch(rectangle)
        rx, ry = rectangle.get_xy()
        cx = rx + rectangle.get_width()/2
        cy = ry + rectangle.get_height()/2
        ax.annotate(lab, (cx, cy), ha='center', va='center')

ax = fig.add_subplot(spec[0], yticks=[], ylabel='Lot')
ax.set_xlim(0, area_w)
ax.set_ylim(0, area_lot_h)
draw_box(ax, lot_generator)

ax = fig.add_subplot(spec[1], yticks=[], ylabel='Machine')
ax.set_xlim(0, area_w)
ax.set_ylim(0, area_machine_h)
draw_box(ax, machine_generator)

plt.show()

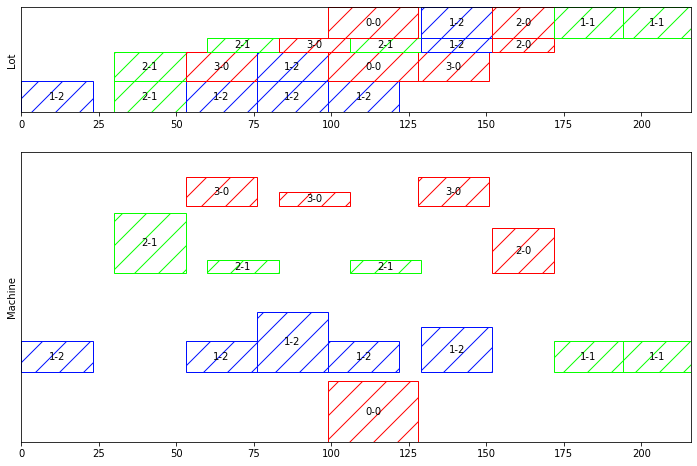
ボックスの色はファミリーを表している。中のラベルはマシン番号とファミリー番号。
ファミリーの切り替えロスを避けるために、同じファミリーをなるべく連続して生産している。
同じファミリーであれば、マシンのキャパシティの範囲で、まとめ生産が可能。

#おわりに

• 少し複雑な問題でも手軽に最適解が得られることは驚異的。
• Interval変数とOptional属性を使用すると生産計画モデルを簡単に表現することができる。
• ロット数1000でも解が得られるかどうかは未検証。Community Editionでは変数が多すぎる。