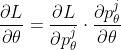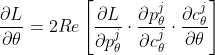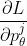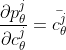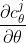この記事は量子コンピューター Advent Calendar 2022の19日目の記事です。
自己紹介
大阪大学で量子コンピュータの研究開発をやっておりますエンジニアの森と申します。
今年の5月から大阪大学のQIQBという組織に参加しまして、量子機械学習をやっているのですが、Qulacs や scikit-qulacs の中の人もやっています。
(※実際の実装は大阪大学を始めとした情報学科系の競プロをやっている、つよつよエンジニア達が開発しているんですけどね!)
Qulacsについては、量子コンピューター Advent Calendar 2022 の 5日目に新機能の紹介をさせて頂きました。
今日は、量子機械学習のライブラリである scikit-qulacsの紹介をさせて頂こうと思います。
scikit-qulacs とは
量子回路シミュレータ Qulacs をバックエンドとした量子機械学習アルゴリズムのシミュレータです。 scikit-learn の名前をもじっています。
コンセプト
未だ黎明期にある量子機械学習アルゴリズムを評価するために今一番必要とされているのは、「きれいな」環境での評価です。
そこで scikit-qulacs は、量子機械学習アルゴリズムをノイズの無いシミュレータで簡単に評価するために実装しています。
量子機械学習 とは
量子機械学習とは、簡単に言ってしまうと、量子コンピュータを使って機械学習を行うことです。
詳しい説明は、scikit-qulacsのチュートリアルを見て頂ければと思います。
また丁度、別のAdvent Calendarで、量子機械学習と古典の量子機械学習を組み合わせて自然言語処理を行うという面白い取り組みをされている記事がありました。
この記事のQCL(量子回路学習)とはを参照頂ければと思います。
この記事では、量子機械学習の中身の実装に少し触れたいと思います。
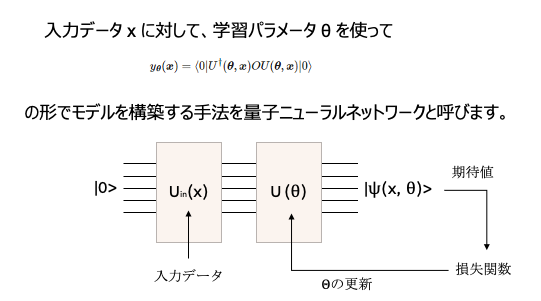
学習の流れ
量子機械学習では、Uinの回路にデータを埋め込み、U(θ)のパラメータ回路(変分回路ansatz)のθを調整することにより学習します。
U(θ)は回転ゲートで構築され、三角関数の組み合わせで関数が近似されるイメージとなります。
学習データの埋め込み
scikit-qulacsのv0.4.1の定義済み回路からデータ埋め込みの所を見て見ましょう。
circuit = LearningCircuit(n_qubit)
for i in range(n_qubit):
# Capture copy of i by `i=i`.
# Without this, i in lambda is a reference to the i, so the lambda always
# recognize i as n_qubit - 1.
circuit.add_input_RY_gate(i, lambda x, i=i: np.arcsin(preprocess_x(x, i)))
circuit.add_input_RZ_gate(
i, lambda x, i=i: np.arccos(preprocess_x(x, i) * preprocess_x(x, i))
)
add_input_RY_gate()とadd_input_RZ_gateでRyとRzの回転ゲートを使ってデータを埋め込んでいます。
preprocess_x()は、以下のように回転ゲートとなるため、-1から1の範囲で埋め込んでいます。
def preprocess_x(x: NDArray[np.float_], index: int) -> float:
xa = x[index % len(x)]
return min(1, max(-1, xa))
add_input_RY_gate()の第二引数にlambda x, i=i: np.arcsin(preprocess_x(x, i))のように関数の形で指定しています。
学習時や推論時に指定されたデータが埋め込まれます。
埋め込み時に更にarcsin()やarccos()で変換して埋め込みます。これは回路やデータによって、調整する必要があります。
このようにscikit-qulacsでは、様々な論文の量子回路を定義済み回路として実装しています。
にjupyter notebook形式で定義済み回路の説明を用意しております。
データは各量子ビットに対して、1個の同じデータが埋め込まれます。そのデータがU(θ)によって変換され出力されます。
量子コンピュータでは、出力は0か1になります。量子機械学習ではサンプリングすることにより、期待値を求めて学習や推論に使用します。
scikit-qulacs は、量子回路シミュレータを使用しており、内部に量子状態を保持しているため、期待値が簡単に取り出せることができます。そのため効率よく量子機械学習を試すことが可能です。
学習
scikit-qulacs は、回帰(regressor)と分類(classifier)を実装しています。
(他にもカーネル法や生成等も実装していますが。)
回帰/分類を様々なパラメータやOptimizerを使用して学習できるように統一したインターフェイスを用意しています。
それが Solver です。
最適化手法として、Nelder-Mead/BFGSを実装しており、これらは SciPy の minimize() により実行されます。
また、 Adam を使用した誤差逆伝播法も実装しています。
以下に学習部分のコード例を載せます。
from skqulacs.qnn import QNNRegressor
n_qubit = 4
depth = 6
time_step = 0.5
solver = Bfgs()
maxiter= 30
circuit = create_qcl_ansatz(n_qubit, depth, time_step, 0)
qnn = QNNRegressor(circuit, solver)
opt_loss, opt_params = qnn.fit(x_train, y_train, maxiter)
print("trained parameters", opt_params)
print("loss", opt_loss)
scikit-qulacsのチュートリアル からの抜粋ですが、create_qcl_ansatz()で定義済み回路を作成して、QNNRegressor()に回路とSolverを指定します。
そして、fit()を呼び出せば学習が実行されます。
パラメータシフト法
学習には、勾配計算が必要になります。量子コンピュータの勾配計算手法として、パラメータシフト法があります。
このパラメータシフト法やQCL(量子回路学習)は、大阪大学の以下の論文で発案されたものです。
[1803.00745] Quantum Circuit Learning
パラメータシフト法はパラメータθの目的関数Lの勾配を以下の計算式で求めることができます。
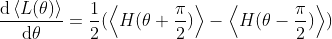
差分法に似ていますが、パラメータを大きくシフトさせて差分を取るため誤差に強いというメリットがあります。
Qulacsの実装
Qulacsには、パラメータシフト法による勾配計算の関数が実装されています。
#define _USE_MATH_DEFINES
#include "GradCalculator.hpp"
#include <math.h>
#include "causalcone_simulator.hpp"
std::vector<std::complex<double>> GradCalculator::calculate_grad(
ParametricQuantumCircuit& circuit, Observable& obs,
std::vector<double> theta) {
ParametricQuantumCircuit* circuit_copy = circuit.copy();
UINT parameter_count = circuit_copy->get_parameter_count();
std::vector<std::complex<double>> grad(parameter_count);
for (UINT target_gate_itr = 0; target_gate_itr < parameter_count;
target_gate_itr++) {
std::complex<double> plus_delta, minus_delta;
{
for (UINT q = 0; q < parameter_count; ++q) {
if (target_gate_itr == q) {
circuit_copy->set_parameter(q, theta[q] + M_PI_2);
} else {
circuit_copy->set_parameter(q, theta[q]);
}
}
CausalConeSimulator tmp(*circuit_copy, obs);
plus_delta = tmp.get_expectation_value();
}
{
for (UINT q = 0; q < parameter_count; ++q) {
if (target_gate_itr == q) {
circuit_copy->set_parameter(q, theta[q] - M_PI_2);
} else {
circuit_copy->set_parameter(q, theta[q]);
}
}
CausalConeSimulator tmp(*circuit_copy, obs);
minus_delta = tmp.get_expectation_value();
}
grad[target_gate_itr] = (plus_delta - minus_delta) / 2.0;
}
delete circuit_copy;
return grad;
};
std::vector<std::complex<double>> GradCalculator::calculate_grad(
ParametricQuantumCircuit& x, Observable& obs) {
std::vector<double> initial_parameter;
for (UINT i = 0; i < x.get_parameter_count(); ++i) {
initial_parameter.push_back(x.get_parameter(i));
}
return calculate_grad(x, obs, initial_parameter);
};
calculate_grad()に対して、Observableで表現される目的関数Lを指定します。
以下のようにCausalConeSimulatorを使用して、期待値を求め勾配計算を行います。
for (UINT q = 0; q < parameter_count; ++q) {
if (target_gate_itr == q) {
circuit_copy->set_parameter(q, theta[q] + M_PI_2);
} else {
circuit_copy->set_parameter(q, theta[q]);
}
}
CausalConeSimulator tmp(*circuit_copy, obs);
plus_delta = tmp.get_expectation_value();
誤差逆伝播法(backpropagation)
パラメータシフト法は、2×パラメータ数×forward propagation のオーダの計算が必要となります。
シミュレータを使う場合、このforward propagationの計算に時間がかかるため、効率が悪くなってしまいます。
そこで、scikit-qulacs では、ディープニューラルネットワークで使わている誤差逆伝播法を実装しています。
量子機械学習の誤差逆伝播法を扱った論文には、以下があります。
図にすると以下のようになります。
まず一度forward propagationを最後まで実行します。
その状態に対して、Observableで表現される目的関数Lを適用します。
その値を微分して、backprop_inner_product()に渡し各レイヤの勾配計算を行います。
std::vector<double> ParametricQuantumCircuit::backprop(
GeneralQuantumOperator* obs) {
//オブザーバブルから、最終段階での微分値を求めて、backprop_from_stateに流す関数
//上側から来た変動量 * 下側の対応する微分値 =
//最終的な変動量になるようにする。
int n = this->qubit_count;
QuantumState* state = new QuantumState(n);
state->set_zero_state();
this->update_quantum_state(state); //一度最後までする
QuantumState* bistate = new QuantumState(n);
QuantumState* Astate = new QuantumState(n); //一時的なやつ
obs->apply_to_state(Astate, *state, bistate);
bistate->multiply_coef(2);
/*一度stateを最後まで求めてから、さらにapply_to_state している。
なぜなら、量子のオブザーバブルは普通の機械学習と違って、二乗した値の絶対値が観測値になる。
二乗の絶対値を微分したやつと、値の複素共役*2は等しい
オブザーバブルよくわからないけど、テストしたらできてた
*/
//ニューラルネットワークのbackpropにおける、後ろからの微分値的な役目を果たす
auto ans = backprop_inner_product(bistate);
delete bistate;
delete state;
delete Astate;
return ans;
}
std::vector<double> ParametricQuantumCircuit::backprop_inner_product(
QuantumState* bistate) {
// circuitを実行した状態とbistateの、inner_productを取った結果を「値」として、それを逆誤差伝搬します
// bistateはノルムが1のやつでなくてもよい
int n = this->qubit_count;
QuantumState* state = new QuantumState(n);
//これは、ゲートを前から適用したときの状態を示す
state->set_zero_state();
this->update_quantum_state(state); //一度最後までする
int num_gates = this->gate_list.size();
std::vector<int> inverse_parametric_gate_position(num_gates, -1);
for (UINT i = 0; i < this->get_parameter_count(); i++) {
inverse_parametric_gate_position[this->_parametric_gate_position[i]] =
i;
}
std::vector<double> ans(this->get_parameter_count());
/*
現在、2番のゲートを見ているとする
ゲート 0 1 2 3 4 5
state | bistate
前から2番までのゲートを適用した状態がstate
最後の微分値から逆算して3番までgateの逆行列を掛けたのがbistate
1番まで掛けて、YのΘ微分した行列を掛けたやつと、bistateの内積の実数部分をとれば答えが出ることが知られている(知られてないかも)
ParametricR? の微分値を計算した行列は、Θに180°を足した行列/2 と等しい
だから、2番まで掛けて、 R?(π) を掛けたやつと、bistateの内積を取る
さらに、見るゲートは逆順である。
だから、最初にstateを最後までやって、ゲートを進めるたびにstateに逆行列を掛けている
さらに、bistateが複素共役になっていることを忘れると、bistateに転置行列を掛ける必要がある。
しかしこのプログラムではbistateはずっと複素共役なので、転置して共役な行列を掛ける必要がある。
ユニタリ性より、転置して共役な行列 = 逆行列
なので、両社にadjoint_gateを掛けている
*/
QuantumState* Astate = new QuantumState(n); //一時的なやつ
for (int i = num_gates - 1; i >= 0; i--) {
QuantumGateBase* gate_now = this->gate_list[i]; // sono gate
if (inverse_parametric_gate_position[i] != -1) {
Astate->load(state);
QuantumGateBase* RcPI;
if (gate_now->get_name() == "ParametricRX") {
RcPI = gate::RX(gate_now->get_target_index_list()[0], M_PI);
} else if (gate_now->get_name() == "ParametricRY") {
RcPI = gate::RY(gate_now->get_target_index_list()[0], M_PI);
} else if (gate_now->get_name() == "ParametricRZ") {
RcPI = gate::RZ(gate_now->get_target_index_list()[0],
M_PI); // 本当はここで2で割りたいけど、行列を割るのは実装が面倒
} else if (gate_now->get_name() == "ParametricPauliRotation") {
ClsParametricPauliRotationGate* pauli_gate_now =
(ClsParametricPauliRotationGate*)gate_now;
RcPI =
gate::PauliRotation(pauli_gate_now->get_target_index_list(),
pauli_gate_now->get_pauli()->get_pauli_id_list(), M_PI);
} else {
std::stringstream error_message_stream;
error_message_stream
<< "Error: " << gate_now->get_name()
<< " does not support backprop in parametric";
throw NotImplementedException(error_message_stream.str());
}
RcPI->update_quantum_state(Astate);
ans[inverse_parametric_gate_position[i]] =
state::inner_product(bistate, Astate).real() /
2.0; //だからここで2で割る
delete RcPI;
}
auto Agate = gate_now->get_inverse();
Agate->update_quantum_state(bistate);
Agate->update_quantum_state(state);
delete Agate;
}
delete Astate;
delete state;
return ans;
}
backprop()から渡された微分値(bistate)を使って、レイヤの後ろからたどっていきながら(get_inverse()を実行する)勾配計算を行います。
勾配計算は、以下の式の右辺の通りに、そのレイヤの状態に対して、回転ゲートの微分値を適用し、
微分値(bistate)との内積を計算し求めます。
まとめ
scikit-qulacs の概要、チュートリアルと内部実装を簡単ですが紹介させて頂きましたがいかがでしたでしょうか?
scikit-qulacs では、様々な論文の回路を定義済み回路として用意しており、簡単に試すことができますので、是非使ってみてください!!
おまけ
まだきちんと読めていないのですが、[2212.02521] Deep quantum neural networks equipped with backpropagation on a superconducting processor は、実機の量子コンピュータで誤差逆伝播法を行っているそうです。