O(N^3)より高速なアルゴリズムを使って、行列行列積を早くしよう part1

目的

以前の記事に書いたように、行列行列積は$O\left(N^3\right)$より少ない計算量で計算できます.

以前の結果では行列行列積を$O\left(N^3\right)$より少ない計算量で計算するアルゴリズムの一つであるStrassenの方法が通常の方法に勝つのはかなり大きなNになるだろうと結論づけましたが、「実装が悪い」（意訳）と言われてしまったので、頑張って高速化しました。

Strassenのアルゴリズムは、行列の分解を再帰的に行うことで、計算量を$O\left(N^{log_27}\right)$で行うアルゴリズムでしたが、この記事では行列の分解を再帰的には行わず、1回だけ用いて計算することにします。
計算量は$O\left(\frac{7}{8}N^3\right)$となるので（この書き方は正しくはありませんが）、十分大きな$N$において$\frac{7}{8}$倍の計算時間で計算できるはずです。

Strassenのアルゴリズムについては以前の記事を参照してください。

ソースコード

実行コードをそのまま貼り付けます。
行列サイズがKになっていたりしていて汚いですが、ご容赦ください。

#include<cstdlib>
#include<cstdio>
#include<vector>
#include<string>
#include<cassert>
#include<ctime>
#include<cmath>
#include<chrono>

void ordinary(
    const std::vector<std::vector<double>>& A, const std::vector<std::vector<double>>& B, std::vector<std::vector<double>>& C,
    const size_t N_begin, const size_t N_end, const size_t M_begin, const size_t M_end, const size_t L_begin, const size_t L_end){
  for(size_t i=N_begin; i<N_end; ++i){
    for(size_t j=M_begin; j<M_end; ++j){
      for(size_t k=L_begin; k<L_end; ++k){
        C[i][k] += A[i][j]*B[j][k];
      }
    }
  }
  return;
}

void Strassen(
    const std::vector<std::vector<double>>& A, const std::vector<std::vector<double>>& B, std::vector<std::vector<double>>& C,
    const size_t N_begin, const size_t N_end, const size_t M_begin, const size_t M_end, const size_t L_begin, const size_t L_end){

  const size_t N_mid = (N_begin + N_end)/2;
  const size_t M_mid = (M_begin + M_end)/2;
  const size_t L_mid = (L_begin + L_end)/2;

  assert(N_end-N_mid == N_mid-N_begin);
  assert(M_end-M_mid == M_mid-M_begin);
  assert(L_end-L_mid == L_mid-L_begin);

  const size_t N_shift = N_mid-N_begin;
  const size_t M_shift = M_mid-M_begin;
  const size_t L_shift = L_mid-L_begin;

  std::vector<std::vector<double>> B11(M_mid, std::vector<double>(L_mid));
  std::vector<std::vector<double>> B13(M_mid, std::vector<double>(L_mid));
  std::vector<std::vector<double>> B14(M_mid, std::vector<double>(L_mid));
  std::vector<std::vector<double>> B16(M_mid, std::vector<double>(L_mid));
  std::vector<std::vector<double>> B17(M_mid, std::vector<double>(L_mid));

  for(size_t j=M_begin; j<M_mid; ++j){
    const double* B1 = B[j].data();
    const double* B2 = B[j].data()+L_shift;
    const double* B3 = B[j+M_shift].data();
    const double* B4 = B[j+M_shift].data()+L_shift;
    for(size_t k=L_begin; k<L_mid; ++k){
      B11[j][k] = B1[k]+B4[k];
      B13[j][k] = B2[k]-B4[k];
      B14[j][k] = B3[k]-B1[k];
      B16[j][k] = B1[k]+B2[k];
      B17[j][k] = B3[k]+B4[k];
    }
  }

  std::vector<double> tmp11(L_mid);
  std::vector<double> tmp12(L_mid);
  std::vector<double> tmp13(L_mid);
  std::vector<double> tmp14(L_mid);
  std::vector<double> tmp15(L_mid);
  std::vector<double> tmp16(L_mid);
  std::vector<double> tmp17(L_mid);

  for(size_t i=N_begin; i<N_mid; ++i){
    for(size_t k=0; k<L_mid; ++k){
      tmp11[k] = 0.0;
      tmp12[k] = 0.0;
      tmp13[k] = 0.0;
      tmp14[k] = 0.0;
      tmp15[k] = 0.0;
      tmp16[k] = 0.0;
      tmp17[k] = 0.0;
    }
    for(size_t j=M_begin; j<M_mid; ++j){
      const double A11 = A[i][j]+A[i+N_shift][j+M_shift];
      const double* B21 = B11[j].data();
      for(size_t k=L_begin; k<L_mid; ++k){
        tmp11[k] += A11*B21[k];
      }
    }
    for(size_t j=M_begin; j<M_mid; ++j){
      const double A12 = A[i+N_shift][j]+A[i+N_shift][j+M_shift];
      const double* B1 = B[j].data();
      for(size_t k=L_begin; k<L_mid; ++k){
        tmp12[k] += A12*B1[k];
      }
    }
    for(size_t j=M_begin; j<M_mid; ++j){
      const double A1 = A[i][j];
      const double* B23 = B13[j].data();
      for(size_t k=L_begin; k<L_mid; ++k){
        tmp13[k] += A1*B23[k];
      }
    }
    for(size_t j=M_begin; j<M_mid; ++j){
      const double A4 = A[i+N_shift][j+M_shift];
      const double* B24 = B14[j].data();
      for(size_t k=L_begin; k<L_mid; ++k){
        tmp14[k] += A4*B24[k];
      }
    }
    for(size_t j=M_begin; j<M_mid; ++j){
      const double A15 = A[i][j]+A[i][j+M_shift];
      const double* B4 = B[j+M_shift].data()+L_shift;
      for(size_t k=L_begin; k<L_mid; ++k){
        tmp15[k] += A15*B4[k];
      }
    }
    for(size_t j=M_begin; j<M_mid; ++j){
      const double A16 = A[i+N_shift][j]-A[i][j];
      const double* B26 = B16[j].data();
      for(size_t k=L_begin; k<L_mid; ++k){
        tmp16[k] += A16*B26[k];
      }
    }
    for(size_t j=M_begin; j<M_mid; ++j){
      const double A17 = A[i][j+M_shift]-A[i+N_shift][j+M_shift];
      const double* B27 = B17[j].data();
      for(size_t k=L_begin; k<L_mid; ++k){
        tmp17[k] += A17*B27[k];
      }
    }

    double* C1 = C[i].data();
    double* C2 = C[i].data()+L_shift;
    double* C3 = C[i+N_shift].data();
    double* C4 = C[i+N_shift].data()+L_shift;
    for(size_t k=L_begin; k<L_mid; ++k){
      C1[k] = tmp11[k]+tmp14[k]-tmp15[k]+tmp17[k];
      C2[k] = tmp13[k]+tmp15[k];
      C3[k] = tmp12[k]+tmp14[k];
      C4[k] = tmp11[k]-tmp12[k]+tmp13[k]+tmp16[k];
    }
  }

  return;
}

void analyze_data(const std::vector<double>& values, double& ave, double& err){
  ave = 0.0;
  for(double value : values){
    ave += value;
  }
  ave /= values.size();
  double var = 0.0;
  for(double value : values){
    var += (value-ave)*(value-ave);
  }

  var /= values.size()-1;
  err = sqrt(var/values.size());
  return;
}

int main(void){
  size_t P = 16;
  srand(0);

  FILE *fp;
  std::string filename = "result.dat";
  fp = fopen(filename.c_str(), "w");
  fprintf(fp, "#K ordinary-time[ms] err[ms] Present-time[ms] err[ms] ratio\n");
  fclose(fp);

  std::chrono::system_clock::time_point start, end;

  for(size_t K=128; K<=1024*4; K*=2){
    std::vector<double> time1(P), time2(P);
    for(size_t p=0; p<P; ++p){
      std::vector<std::vector<double>> A(K, std::vector<double>(K));
      std::vector<std::vector<double>> B(K, std::vector<double>(K));
      std::vector<std::vector<double>> C1(K, std::vector<double>(K));
      std::vector<std::vector<double>> C2(K, std::vector<double>(K));

      for(size_t i=0; i<K; ++i){
        for(size_t j=0; j<K; ++j){
          A[i][j] = ((double)rand())/RAND_MAX;
          B[i][j] = ((double)rand())/RAND_MAX;
        }
      }

      start = std::chrono::system_clock::now();
      ordinary(A, B, C1, 0, K, 0, K, 0, K);
      end = std::chrono::system_clock::now();
      double time1_tmp = std::chrono::duration_cast<std::chrono::milliseconds>(end-start).count();
      start = std::chrono::system_clock::now();
      Strassen(A, B, C2, 0, K, 0, K, 0, K);
      end = std::chrono::system_clock::now();
      double time2_tmp = std::chrono::duration_cast<std::chrono::milliseconds>(end-start).count();

      time1[p] = time1_tmp;
      time2[p] = time2_tmp;
    }

    double time1_ave, time1_err;
    double time2_ave, time2_err;

    analyze_data(time1, time1_ave, time1_err);
    analyze_data(time2, time2_ave, time2_err);

    fp = fopen(filename.c_str(), "a");
    fprintf(fp, "%zu %lf %lf %lf %lf %lf\n", K, time1_ave, time1_err, time2_ave, time2_err, time2_ave/time1_ave);
    fclose(fp);
  }

  return 0;
}

ordinaryが通常の行列行列積を計算するコード、Strassenが今回の方法による行列行列積の計算コードになります。
Strassen内の3重ループが7つあるところが重要で、それぞれのループ内の計算が$\left(N/2\right)^2$回かかるので、全体で$\frac{7}{8}N^3 + O\left(N^2\right)$回の計算コストとなり、通常の方法の計算コスト$N^3$に十分大きなNで勝つだろう、ということを期待しています。

実行環境

・CPU: Intel Core i5
・Memory: 4GB
・コンパイラ: g++ version 4.9.3
・最適化オプション: -O3

結果

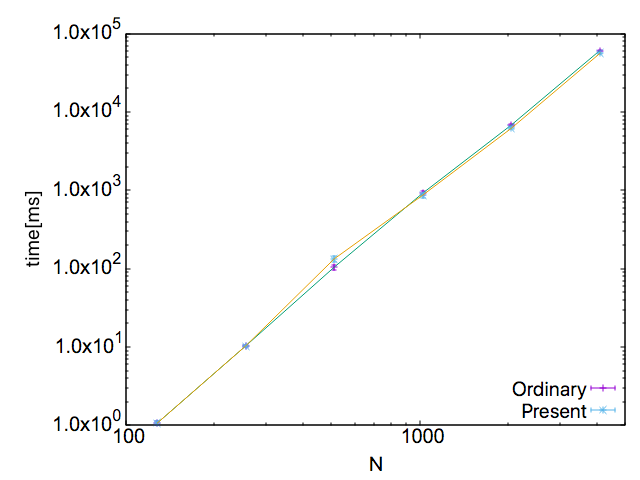
横軸行列サイズ、縦軸実行時間[ms]のグラフがこちらです。
どちらの方法も計算コストは$O\left(N^3\right)$であるため、両対数グラフで傾きが3（横方向に値を10倍したら、縦方向に1000倍になる）の直線の結果となっていて綺麗ですね。

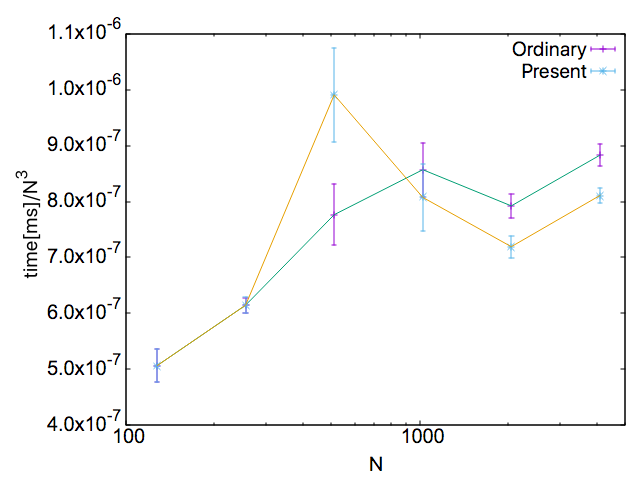
通常の結果(Ordinary)と今回の方法の結果(Present)の違いが見えにくいので、縦軸を規格化します。
計算コストが$O\left(N^3\right)$なので、縦軸の値を実行時間/(行列サイズ)^3にします。

行列サイズが小さい範囲では今回の方法による計算時間は通常の方法よりも遅いですが、行列サイズが大きい範囲では逆に今回の方法による計算時間が通常の方法よりも早くなっていることが分かります。

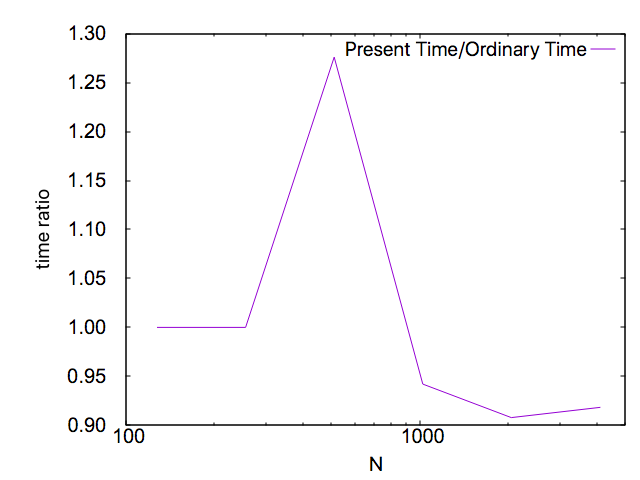
次に、計算時間の平均値の比を見てみます。

行列サイズが大きい所では、今回の方法による計算時間が通常の方法より1割弱短いことが分かります。目標とした値である$\frac{7}{8}=0.875$よりも大きいのは、$O\left(N^2\right)$の計算時間がかかる処理が無視できないためであると考えられます。