対象
この記事は
- 量子スピン系のハミルトニアンの対角化方法が分からない人
- 量子スピン系の小さいモデルでちょっと遊んでみたいけど,いちいち専用ライブラリを使うのはめんどくさい人
向けの記事です.
初学者向けなので,最適化とかは真面目にはやりません.
基本的にpythonで解説しています.最後にちょっとjuliaのコードもあります.
環境は,pythonでnumpyとscipyが動けば大丈夫です.
juliaの場合はArpack, SparseArraysが必要です.
はじめに
プログラムと整合性を取りやすい様に,添字は0から始めます.
簡単のため,スピンは$\pm 1$のみをとるとします.
この記事では
I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} ~ , ~
S^x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} ~ , ~
S^y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} ~ , ~
S^z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
とします.
いくら初学者向けとは言ってもスピン数が少なすぎると悲しいので,(N=16ぐらいの)そこそこのスピン数の基底状態計算がノートPCでもちょっと待てば動く様なコードを目指します.
(でもN=16って2次元正方格子だとL=4だし,4次元超立方格子だとL=2しかないので悲しい.)
それと,私は対角化の人ではないので,間違ったこと書いてるかもしれません.先に謝っておきます.ごめんなさい.
ハミルトニアンと行列
スピン模型のハミルトニアンは
\mathcal{H} = \sum_{\langle i, j \rangle} J_x S^x_i S^x_j + J_y S^y_i S^y_j + J_z S^z_i S^z_j
のような形で書かれることが多いですが,ハミルトニアンの行列表示において,$S^x_i S^x_j$などの積はテンソル積を意味します.
テンソル積は,行列A, Bに対して
A \otimes B = \left( a_{ij} B \right) =
\begin{pmatrix}
a_{11} B & a_{12} B & \cdots \\
a_{21} B & a_{22} B & \cdots \\
\vdots & \vdots & \ddots
\end{pmatrix}
と表される演算です (Wikidepdiaより)
更に,$i, j$で指定されていないindexには全て単位行列$I$がかかります.
つまり先ほどのハミルトニアンの$i=0, j=1$の時の$\sum$の中身は,
J_x S^x \otimes S^x \otimes I \otimes I \otimes \dots + \\
J_y S^y \otimes S^y \otimes I \otimes I \otimes \dots + \\
J_z S^z \otimes S^z \otimes I \otimes I \otimes \dots \ \
と計算できます.よって,先ほどのハミルトニアンを行列表示できちんと書くと
\mathcal{H} = \sum_{\langle i, j \rangle}
J_x \ I \otimes \cdots \otimes I \otimes
\underset{\underset{i}{\wedge}}{S^x} \otimes I \otimes \cdots \otimes I \otimes \underset{\underset{j}{\wedge}}{S^x} \otimes I \otimes \cdots + \\
J_y \ I \otimes \cdots \otimes I \otimes
\underset{\underset{i}{\wedge}}{S^y} \otimes I \otimes \cdots \otimes I \otimes \underset{\underset{j}{\wedge}}{S^y} \otimes I \otimes \cdots + \\
J_z \ I \otimes \cdots \otimes I \otimes
\underset{\underset{i}{\wedge}}{S^z} \otimes I \otimes \cdots \otimes I \otimes \underset{\underset{j}{\wedge}}{S^z} \otimes I \otimes \cdots
となります.これを定義に従って計算するのは大変ですが,実際はほとんどが0となります.
実際に0以外の値が入るindexは,まず$(x, y) = (0, 0)$として,テンソル積を構成する行列を後ろから見て,
- (x, y) を 2倍にする
- (x, y) に 行列の成分が非零となるindexを加える
(例. $I$,$S^z$だったら$(0, 0)$ or $(1, 1)$, $S^x$,$S^y$だったら$(0, 1)$ or $(1, 0)$) - 一つ前の行列に移動する
というステップを繰り返すことで,最終的に成分が入るindexを計算することができます.値も同様に計算できます.
ここで,1ステップ目の"2倍"の2という数字は,$SやI$の行列サイズが2だからです.異なる行列サイズの場合はここを変えてください.
この方法から分かるように,このハミルトニアンを表す行列の非零成分は,2ステップ目のindexを加える過程で毎回2倍に増えるので,近接相互作用のみの場合,$O(結合数 \times 2^N) \approx O(N 2^N)$となります.行列自体は$2^N$行$2^N$列なので,効率よく行列を生成することができます.
簡単な実装
簡単な実装のための準備をします.
def set_Hamiltonian_tmp(O1, index1, O2, index2, x, y, itr, val, matrix):
if(val==0):
return
if(itr>=0):
if(itr==index1):
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x, 2*y, itr-1, val*O1[0][0], matrix)
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x+1, 2*y, itr-1, val*O1[1][0], matrix)
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x, 2*y+1, itr-1, val*O1[0][1], matrix)
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x+1, 2*y+1, itr-1, val*O1[1][1], matrix)
elif(itr==index2):
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x, 2*y, itr-1, val*O2[0][0], matrix)
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x+1, 2*y, itr-1, val*O2[1][0], matrix)
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x, 2*y+1, itr-1, val*O2[0][1], matrix)
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x+1, 2*y+1, itr-1, val*O2[1][1], matrix)
else:
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x, 2*y, itr-1, val, matrix)
set_Hamiltonian_tmp(O1, index1, O2, index2, 2*x+1, 2*y+1, itr-1, val, matrix)
else:
matrix[x,y] += val
return
def set_Hamiltonian(O1, index1, O2, index2, J, matrix, N):
set_Hamiltonian_tmp(O1, index1, O2, index2, 0, 0, N-1, J, matrix)
return
set_Hamiltonian_tmpを再帰的に呼んで,非零行列要素の場所と値を計算しています.
このset_Hamiltonian_tmpが先ほどのアルゴリズムを表しています.
このような準備をしておくと,Nスピンの1次元ハイゼンベルグ模型のハミルトニアン
\mathcal{H} = \sum_{i} J_x S^x_i S^x_{i+1} + J_y S^y_i S^y_{i+1} + J_z S^z_i S^z_{i+1}
($J_x = J_y = J_z = 1$)が(周期境界条件で)次のようにして求まります.
import numpy as np
Sx = np.array(([0, 1], [1, 0]), dtype=np.complex128)
Sy = np.array(([0, -1j], [1j, 0]), dtype=np.complex128)
Sz = np.array(([1, 0], [0, -1]), dtype=np.complex128)
N = 12
Jx = 1.0
Jy = 1.0
Jz = 1.0
hamiltonian = np.zeros((2**N, 2**N), dtype=np.complex128)
for i in range(N-1):
set_Hamiltonian(Sx, i, Sx, i+1, Jx, hamiltonian, N)
set_Hamiltonian(Sy, i, Sy, i+1, Jy, hamiltonian, N)
set_Hamiltonian(Sz, i, Sz, i+1, Jz, hamiltonian, N)
set_Hamiltonian(Sx, N-1, Sx, 0, Jx, hamiltonian, N)
set_Hamiltonian(Sy, N-1, Sy, 0, Jy, hamiltonian, N)
set_Hamiltonian(Sz, N-1, Sz, 0, Jz, hamiltonian, N)
このハミルトニアンを対角化したい場合は,
from numpy.linalg import eigh
eigs, eigvals = eigh(hamiltonian)
とすれば求まるはずです.
高速化する
先ほどの実装は遅すぎます.
密行列の固有値と固有ベクトルを全て求めると当然時間がかかります.
必要がないならやめましょう.
疎行列
ハミルトニアンに$I$が多いので,ハミルトニアンを表す行列成分に0が多くなります.
なので,実際に0以外の成分が入るとこをのみを計算するようにしましょう.
pythonのscipy.sparse.lil_matrixを用いると,numpyの配列のように疎行列を扱うことができます.
hamiltonian = lil_matrix((2**N, 2**N), dtype=np.complex128)
と変更するだけで大丈夫です.
小さい固有値と対応する固有ベクトル
ハミルトニアンの固有値/固有ベクトルは$2^N$個ありますが,全部必要になることはあまりありません.
エルミート行列の小さい固有値と対応する固有ベクトルのみだけを計算する場合は,scipy.sparse.linalgのeigshを使いましょう.
また,lil_matrixは計算には向かないので,scr_matrix等の形式に変更しましょう.
次の例では,ハミルトニアンの固有値/固有ベクトルを小さい方から6個とってきてます.
from scipy.sparse import csr_matrix
from scipy.sparse.linalg import eigsh
hamiltonian = csr_matrix(hamiltonian)
eigs, eigvecs = eigsh(hamiltonian, which='SA', k=6)
詳しくは,scipyのeigshのページを参照してください.
もうちょっと高速化する
先ほどのコードでも動きますが,まだ計算できるNが小さいです.
N=16程度を高速で計算しようと思ったら,もう少し手間を加える必要があります.
eigshの仕様
Find k eigenvalues and eigenvectors of the real symmetric square matrix or complex hermitian matrix A.
と書いてありますが,eigshのソースコードを読むと
complex hermitian matrices should be solved with eigs
と書いてあります.(実際,複素数成分の行列をeigshに投げると内部でeigsが実行されます)
- エルミート性を仮定するアルゴリズムは,仮定しないアルゴリズムより遅い
- エルミート性を仮定しないアルゴリズム場合,固有ベクトルが直交するとは限らない
という問題があるので,できるだけエルミート性を仮定したアルゴリズムにした方が良いです.
先に挙げたハミルトニアンの場合,実対称行列となっています.なので,
hamiltonian = hamiltonian.astype(np.float64)
のようにして実対称行列に変換してからeigshに投げましょう.
$S^x S^y$のような項があって実対象とはならない場合は,(実際に実行されているのはeigsなので)諦めてeigsを実行後に固有ベクトルを直交化しましょう.
(一応,N行N列エルミート行列を実部と虚部に分解して2N行2N列の対称行列にして実行するテクニックも存在します.)
pythonの疎行列の仕様
はむかずさんのページにあるように,lil_matrixは挿入操作ですら遅いので,最初からcsr_matrixで持っていた方が良いです.
ハミルトニアンの非零成分が
(x_1, y_1, val_1), (x_2, y_2, val_2), (x_3, y_3, val_3), \cdots
の様に表される場合,
x_array = [x_1, x_2, ...]
y_array = [y_1, y_2, ...]
val_array = [val_1, val_2, ...]
hamiltonian = csr_matrix((val_array, (x_array, y_array)), shape=(2**N, 2**N))
とすることで,lil_matrixを経由することなくcsr_matrixが生成できます.
(詳しくはcsr_matrixの仕様を参照してください)
ここで,ハミルトニアンの非零成分についてもう少し詳しく見てみます.
対角成分
対角成分は$S^zS^z$のように,$S^z$のみの項から来ます.この項はどの添字によるものかに関わらず,x_arrayとy_arrayが共通します.なので,
val_arrayのみを計算して足し上げることで,対角成分由来のx_array,y_array,val_arrayの配列の長さを圧縮できます.
def set_Hamiltonian_diag(O1, index1, O2, index2, J, N):
val_array = [J]
for i in range(N-1, -1, -1):
val_array_new = [None]*(len(val_array)*2)
if(i==index1):
val_array_new[::2] = [val*O1[0][0] for val in val_array]
val_array_new[1::2] = [val*O1[1][1] for val in val_array]
elif(i==index2):
val_array_new[::2] = [val*O2[0][0] for val in val_array]
val_array_new[1::2] = [val*O2[1][1] for val in val_array]
else:
val_array_new[::2] = val_array
val_array_new[1::2] = val_array
val_array = val_array_new
return np.array(val_array)
このような関数を実装しておくと,先ほどのハミルトニアンの対角成分は
hamiltonian_diag = np.zeros((2**N), dtype=np.complex128)
for i in range(N-1):
hamiltonian_diag += set_Hamiltonian_diag(Sz, i, Sz, i+1, Jz, N)
hamiltonian_diag += set_Hamiltonian_diag(Sz, N-1, Sz, 0, Jz, N)
のようにして実装できます.(この実装の場合,x_arrayとy_arrayは共に $[0, 1, \cdots, 2^N-1]$ =range(2**N)なので,覚えていません)
非対角成分
非対角成分の場合,異なるindexからくる項は異なる行列成分に属するため,x_array, y_array, val_arrayを全て覚えておく必要があります.
def set_Hamiltonian_offdiag(O1, index1, O2, index2, J, N):
x_array = [0]
y_array = [0]
val_array = [J]
for i in range(N-1, -1, -1):
x_array_new = [None]*(len(x_array)*2)
y_array_new = [None]*(len(y_array)*2)
val_array_new = [None]*(len(val_array)*2)
if(i==index1):
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y+1 for y in y_array]
val_array_new[::2] = [val*O1[0][1] for val in val_array]
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y for y in y_array]
val_array_new[1::2] = [val*O1[1][0] for val in val_array]
elif(i==index2):
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y+1 for y in y_array]
val_array_new[::2] = [val*O2[0][1] for val in val_array]
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y for y in y_array]
val_array_new[1::2] = [val*O2[1][0] for val in val_array]
else:
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y for y in y_array]
val_array_new[::2] = val_array
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y+1 for y in y_array]
val_array_new[1::2] = val_array
x_array = x_array_new
y_array = y_array_new
val_array = val_array_new
return x_array, y_array, val_array
このような関数を実装しておくと,先ほどのハミルトニアンの非対角成分は
x_array = []
y_array = []
val_array = []
for i in range(N-1):
x_array_new, y_array_new, val_array_new = set_Hamiltonian_offdiag(Sx, i, Sx, i+1, Jx, N)
x_array.extend(x_array_new)
y_array.extend(y_array_new)
val_array.extend(val_array_new)
x_array_new, y_array_new, val_array_new = set_Hamiltonian_offdiag(Sy, i, Sy, i+1, Jy, N)
x_array.extend(x_array_new)
y_array.extend(y_array_new)
val_array.extend(val_array_new)
x_array_new, y_array_new, val_array_new = set_Hamiltonian_offdiag(Sx, N-1, Sx, 0, Jx, N)
x_array.extend(x_array_new)
y_array.extend(y_array_new)
val_array.extend(val_array_new)
x_array_new, y_array_new, val_array_new = set_Hamiltonian_offdiag(Sy, N-1, Sy, 0, Jy, N)
x_array.extend(x_array_new)
y_array.extend(y_array_new)
val_array.extend(val_array_new)
の様になります.(この実装の場合もx_arrayは$[0, 1, \cdots, 2^N-1]$ =range(2**N)となりますが,y_arrayだけ書くのは教育的ではない気がしたので書いておきます.)
ただ,非対角成分は項が多いため,出来るだけ数を減らしたいです.
ここで注目するのは,$S^x_i S^x_j$と$S^y_i S^y_j$(と,$S^x_i S^y_j$や$S^y_i S^x_j$)が指す非零成分の場所は全く同じということです.(同様に,$S^z_i S^x_j$と$S^z_i S^y_j$も非零成分の場所が同じになります.非零成分を求めるアルゴリズムを見ると自明です.)なので,まとめてしまいましょう.
def set_Hamiltonian_offdiag(O1_1, O2_1, index1, O1_2, O2_2, index2, J1, J2, N):
x_array = [0]
y_array = [0]
val1_array = [J1]
val2_array = [J2]
for i in range(N-1, -1, -1):
x_array_new = [None]*(len(x_array)*2)
y_array_new = [None]*(len(y_array)*2)
val1_array_new = [None]*(len(val1_array)*2)
val2_array_new = [None]*(len(val2_array)*2)
if(i==index1):
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y+1 for y in y_array]
val1_array_new[::2] = [val*O1_1[0][1] for val in val1_array]
val2_array_new[::2] = [val*O2_1[0][1] for val in val2_array]
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y for y in y_array]
val1_array_new[1::2] = [val*O1_1[1][0] for val in val1_array]
val2_array_new[1::2] = [val*O2_1[1][0] for val in val2_array]
elif(i==index2):
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y+1 for y in y_array]
val1_array_new[::2] = [val*O1_2[0][1] for val in val1_array]
val2_array_new[::2] = [val*O2_2[0][1] for val in val2_array]
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y for y in y_array]
val1_array_new[1::2] = [val*O1_2[1][0] for val in val1_array]
val2_array_new[1::2] = [val*O2_2[1][0] for val in val2_array]
else:
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y for y in y_array]
val1_array_new[::2] = val1_array
val2_array_new[::2] = val2_array
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y+1 for y in y_array]
val1_array_new[1::2] = val1_array
val2_array_new[1::2] = val2_array
x_array = x_array_new
y_array = y_array_new
val1_array = val1_array_new
val2_array = val2_array_new
return x_array, y_array, np.array(val1_array) + np.array(val2_array)
このように,先ほどの$S^xS^x$と$S^yS^y$に関するset_Hamiltonian_offdiag関数を一つにまとめると,先ほどのハミルトニアンの非対角成分は
x_array = []
y_array = []
val_array = []
for i in range(N-1):
x_array_new, y_array_new, val_array_new = set_Hamiltonian_offdiag(Sx, Sy, i, Sx, Sy, i+1, Jx, Jy, N)
x_array.extend(x_array_new)
y_array.extend(y_array_new)
val_array.extend(val_array_new)
x_array_new, y_array_new, val_array_new = set_Hamiltonian_offdiag(Sx, Sy, N-1, Sx, Sy, 0, Jx, Jy, N)
x_array.extend(x_array_new)
y_array.extend(y_array_new)
val_array.extend(val_array_new)
の様になります.
このようにして非対角成分を求めると,先ほどよりも必要な配列サイズが半分になります.
最終的なpythonコード
先ほどまでの事例をまとめると,次の様なコードになります.
import numpy as np
from scipy.sparse import csr_matrix
from scipy.sparse.linalg import eigsh
Sx = np.array(([0, 1], [1, 0]), dtype=np.complex128)
Sy = np.array(([0, -1j], [1j, 0]), dtype=np.complex128)
Sz = np.array(([1, 0], [0, -1]), dtype=np.complex128)
def set_Hamiltonian_diag(O1, index1, O2, index2, J, N):
val_array = [J]
for i in range(N-1, -1, -1):
val_array_new = [None]*(len(val_array)*2)
if(i==index1):
val_array_new[::2] = [val*O1[0][0] for val in val_array]
val_array_new[1::2] = [val*O1[1][1] for val in val_array]
elif(i==index2):
val_array_new[::2] = [val*O2[0][0] for val in val_array]
val_array_new[1::2] = [val*O2[1][1] for val in val_array]
else:
val_array_new[::2] = val_array
val_array_new[1::2] = val_array
val_array = val_array_new
return np.array(val_array)
def set_Hamiltonian_offdiag(O1_1, O2_1, index1, O1_2, O2_2, index2, J1, J2, N):
x_array = [0]
y_array = [0]
val1_array = [J1]
val2_array = [J2]
for i in range(N-1, -1, -1):
x_array_new = [None]*(len(x_array)*2)
y_array_new = [None]*(len(y_array)*2)
val1_array_new = [None]*(len(val1_array)*2)
val2_array_new = [None]*(len(val2_array)*2)
if(i==index1):
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y+1 for y in y_array]
val1_array_new[::2] = [val*O1_1[0][1] for val in val1_array]
val2_array_new[::2] = [val*O2_1[0][1] for val in val2_array]
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y for y in y_array]
val1_array_new[1::2] = [val*O1_1[1][0] for val in val1_array]
val2_array_new[1::2] = [val*O2_1[1][0] for val in val2_array]
elif(i==index2):
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y+1 for y in y_array]
val1_array_new[::2] = [val*O1_2[0][1] for val in val1_array]
val2_array_new[::2] = [val*O2_2[0][1] for val in val2_array]
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y for y in y_array]
val1_array_new[1::2] = [val*O1_2[1][0] for val in val1_array]
val2_array_new[1::2] = [val*O2_2[1][0] for val in val2_array]
else:
x_array_new[::2] = [2*x for x in x_array]
y_array_new[::2] = [2*y for y in y_array]
val1_array_new[::2] = val1_array
val2_array_new[::2] = val2_array
x_array_new[1::2] = [2*x+1 for x in x_array]
y_array_new[1::2] = [2*y+1 for y in y_array]
val1_array_new[1::2] = val1_array
val2_array_new[1::2] = val2_array
x_array = x_array_new
y_array = y_array_new
val1_array = val1_array_new
val2_array = val2_array_new
return x_array, y_array, np.array(val1_array) + np.array(val2_array)
if __name__ == "__main__":
N = 16
Jx = 1.0
Jy = 1.0
Jz = 1.0
hamiltonian_diag = np.zeros((2**N), dtype=np.complex128)
x_array = []
y_array = []
val_array = []
for i in range(N-1):
x_array_new, y_array_new, val_array_new = set_Hamiltonian_offdiag(Sx, Sy, i, Sx, Sy, i+1, Jx, Jy, N)
x_array.extend(x_array_new)
y_array.extend(y_array_new)
val_array.extend(val_array_new)
hamiltonian_diag += set_Hamiltonian_diag(Sz, i, Sz, i+1, Jz, N)
x_array_new, y_array_new, val_array_new = set_Hamiltonian_offdiag(Sx, Sy, N-1, Sx, Sy, 0, Jx, Jy, N)
x_array.extend(x_array_new)
y_array.extend(y_array_new)
val_array.extend(val_array_new)
hamiltonian_diag += set_Hamiltonian_diag(Sz, N-1, Sz, 0, Jz, N)
x_array.extend(range(2**N))
y_array.extend(range(2**N))
val_array.extend(hamiltonian_diag)
hamiltonian = csr_matrix((val_array, (x_array, y_array)), shape=(2**N, 2**N))
hamiltonian = hamiltonian.astype(np.float64)
eigs, eigvecs = eigsh(hamiltonian, which='SA')
print(min(eigs)/N)
(最後に1スピン当たりの基底エネルギーを出力しています)
N=16の1次元ハイゼンベルグ模型の基底状態計算が手元のノートPCで5~6秒ほどで実行できます.
N=20にすると2~3分ぐらいでした.
このくらいなら「ちょっと遊ぶ」のに十分ではないでしょうか.
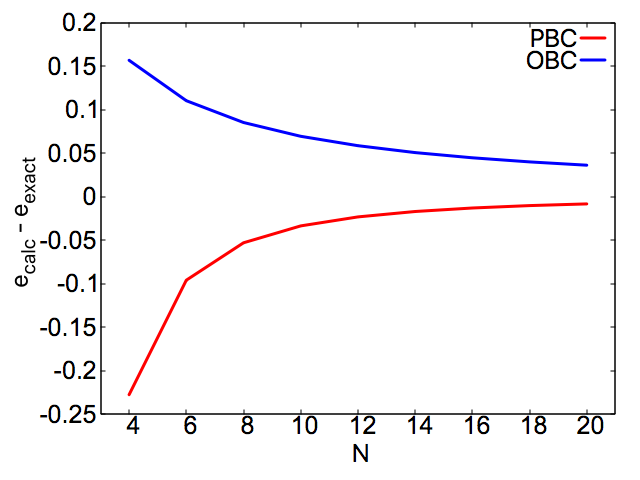
周期境界条件(PBC)と開放境界条件(OBC)で計算した基底エネルギー$e_{calc}$をN無限大極限での厳密解($e_{exact} = 1-4\log2 = -1.772589...$)(このサイトなどを参照)と比較した結果が次です.
| N | $e_calc$ (PBC) | $e_calc$ (OBC) |
|---|---|---|
| 4 | -2.000000 | -1.616025 |
| 6 | -1.868517 | -1.662385 |
| 8 | -1.825547 | -1.687466 |
| 10 | -1.806179 | -1.703214 |
| 12 | -1.795797 | -1.714030 |
| 14 | -1.789586 | -1.721921 |
| 16 | -1.785574 | -1.727934 |
| 18 | -1.782833 | -1.732669 |
| 20 | -1.780877 | -1.736495 |
PBCの結果が先ほどのサイトの結果と一致しているのでアルゴリズムは多分大丈夫ですけど,OBCの結果がちょっと不安ですね......
フェルミオン系やボゾン系の場合
フェルミオン系やボゾン系は全くの専門外なので,コメントだけにしておきます.
フェルミオン系の場合
スピン系は各サイトにつきスピンが上向き,スピンが下向きの2状態でしたが,フェルミオン系の場合は各サイトにつき(上向きスピンの粒子数,下向きスピンの粒子数)= (0, 0), (0, 1), (1, 0), (1, 1) の4通りとなります.
もしくは,(サイトindex, スピンの上下)を((サイト+スピンindex), 粒子の有無)にとして計算することもできます.(やってることは同じです)
なので,それ用にコードを書き換えるだけです.
特に,後者の場合は生成消滅演算子$c^{\dagger}, c$が
c^{\dagger} = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} ~ , ~
c = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}
と書けるので,ある程度先ほどのコードを使い回せます.
また,全粒子数と同時対角化可能(可換)な場合は,ターゲットとする全粒子数に関連する成分のみ取り出すことで,行列サイズを小さくすることができます.
(上向きスピンの粒子数,下向きスピンの粒子数それぞれと可換,というケースもよくあります.)
何か可換な物理量がある場合に行列サイズを小さくして対角化する手法はスピン系でも使えます.
ボゾン系の場合
全粒子数が保存する場合は,サイトとスピンindexを固定すると粒子数は0以上全粒子数以下の全粒子数+1通りなので,頑張れば計算できます.
全粒子数が保存しない場合は,サイトとスピンindexを固定した時の粒子数の最大値を決めて計算し,その最大値を徐々に大きくして外挿する,という方法があるみたいです.(全粒子数が保存する場合も使えます)
juliaのコード
最後のpythonコードのjulia版です.
versionは1.5.2です.
using Arpack
using SparseArrays
function set_Hamiltonian_diag(O1, index1, O2, index2, J, N)
val_array = [J]
for i=1:N
val_array_new = zeros(Complex, length(val_array)*2)
if N+1-i==index1
val_array_new[1:2:length(val_array_new)] = [val*O1[1][1] for val in val_array]
val_array_new[2:2:length(val_array_new)] = [val*O1[2][2] for val in val_array]
elseif N+1-i==index2
val_array_new[1:2:length(val_array_new)] = [val*O2[1][1] for val in val_array]
val_array_new[2:2:length(val_array_new)] = [val*O2[2][2] for val in val_array]
else
val_array_new[1:2:length(val_array_new)] = val_array
val_array_new[2:2:length(val_array_new)] = val_array
end
val_array = val_array_new
end
return val_array
end
function set_Hamiltonian_offdiag(O1_1, O2_1, index1, O1_2, O2_2, index2, J1, J2, N)
x_array = [1]
y_array = [1]
val1_array = [complex(J1)]
val2_array = [complex(J2)]
for i=1:N
x_array_new = zeros(length(x_array)*2)
y_array_new = zeros(length(y_array)*2)
val1_array_new = zeros(Complex, length(val1_array)*2)
val2_array_new = zeros(Complex, length(val2_array)*2)
if N+1-i==index1
x_array_new[1:2:length(x_array_new)] = [2*x-1 for x in x_array]
y_array_new[1:2:length(y_array_new)] = [2*y for y in y_array]
val1_array_new[1:2:length(val1_array_new)] = [val*O1_1[1][2] for val in val1_array]
val2_array_new[1:2:length(val2_array_new)] = [val*O2_1[1][2] for val in val2_array]
x_array_new[2:2:length(x_array_new)] = [2*x for x in x_array]
y_array_new[2:2:length(y_array_new)] = [2*y-1 for y in y_array]
val1_array_new[2:2:length(val1_array_new)] = [val*O1_1[2][1] for val in val1_array]
val2_array_new[2:2:length(val2_array_new)] = [val*O2_1[2][1] for val in val2_array]
elseif N+1-i==index2
x_array_new[1:2:length(x_array_new)] = [2*x-1 for x in x_array]
y_array_new[1:2:length(y_array_new)] = [2*y for y in y_array]
val1_array_new[1:2:length(val1_array_new)] = [val*O1_2[1][2] for val in val1_array]
val2_array_new[1:2:length(val2_array_new)] = [val*O2_2[1][2] for val in val2_array]
x_array_new[2:2:length(x_array_new)] = [2*x for x in x_array]
y_array_new[2:2:length(y_array_new)] = [2*y-1 for y in y_array]
val1_array_new[2:2:length(val1_array_new)] = [val*O1_2[2][1] for val in val1_array]
val2_array_new[2:2:length(val2_array_new)] = [val*O2_2[2][1] for val in val2_array]
else
x_array_new[1:2:length(x_array_new)] = [2*x-1 for x in x_array]
y_array_new[1:2:length(y_array_new)] = [2*y-1 for y in y_array]
val1_array_new[1:2:length(val1_array_new)] = val1_array
val2_array_new[1:2:length(val2_array_new)] = val2_array
x_array_new[2:2:length(x_array_new)] = [2*x for x in x_array]
y_array_new[2:2:length(y_array_new)] = [2*y for y in y_array]
val1_array_new[2:2:length(val1_array_new)] = val1_array
val2_array_new[2:2:length(val2_array_new)] = val2_array
end
x_array = x_array_new
y_array = y_array_new
val1_array = val1_array_new
val2_array = val2_array_new
end
return x_array, y_array, val1_array+val2_array
end
function main()
Sx = [[0, 1], [1, 0]]
Sy = [[0, complex(0, -1)], [complex(0, 1), 0]]
Sz = [[1, 0], [0, -1]]
N = 16
Jx = complex(1.0, 0.0)
Jy = complex(1.0, 0.0)
Jz = complex(1.0, 0.0)
hamiltonian_diag = zeros(Complex, (2^N))
arrays = [zeros(Int, 0), zeros(Int, 0), zeros(Complex, 0)]
for i=1:N-1
arrays_new = set_Hamiltonian_offdiag(Sx, Sy, i, Sx, Sy, i+1, Jx, Jy, N)
append!(arrays[1], arrays_new[1])
append!(arrays[2], arrays_new[2])
append!(arrays[3], arrays_new[3])
hamiltonian_diag += set_Hamiltonian_diag(Sz, i, Sz, i+1, Jz, N)
end
arrays_new = set_Hamiltonian_offdiag(Sx, Sy, N, Sx, Sy, 1, Jx, Jy, N)
append!(arrays[1], arrays_new[1])
append!(arrays[2], arrays_new[2])
append!(arrays[3], arrays_new[3])
hamiltonian_diag += set_Hamiltonian_diag(Sz, N, Sz, 1, Jz, N)
append!(arrays[1], [n for n in 1:2^N])
append!(arrays[2], [n for n in 1:2^N])
append!(arrays[3], hamiltonian_diag)
arrays[3] = real(arrays[3])
hamiltonian = sparse(arrays[1], arrays[2], arrays[3])
eigvals = eigs(hamiltonian, which=:SR)[1]
println(minimum(eigvals)/N)
end
main()
juliaの場合はpythonの時とは異なりeigsを使って固有値を求めていますが,juliaのArpackのeigsはLinearAlgebraのissymmetric(hamiltonian)がtrueの場合は勝手にeigsh相当のアルゴリズムになります.(そもそもeigshが実装されていないです)
配列の添字が1始まりなことと,配列のslicingの方法に注意しましょう.