ABC390の振り返りです。直前でNW繋がらなくなって間に合わなかったのでUnratedです。
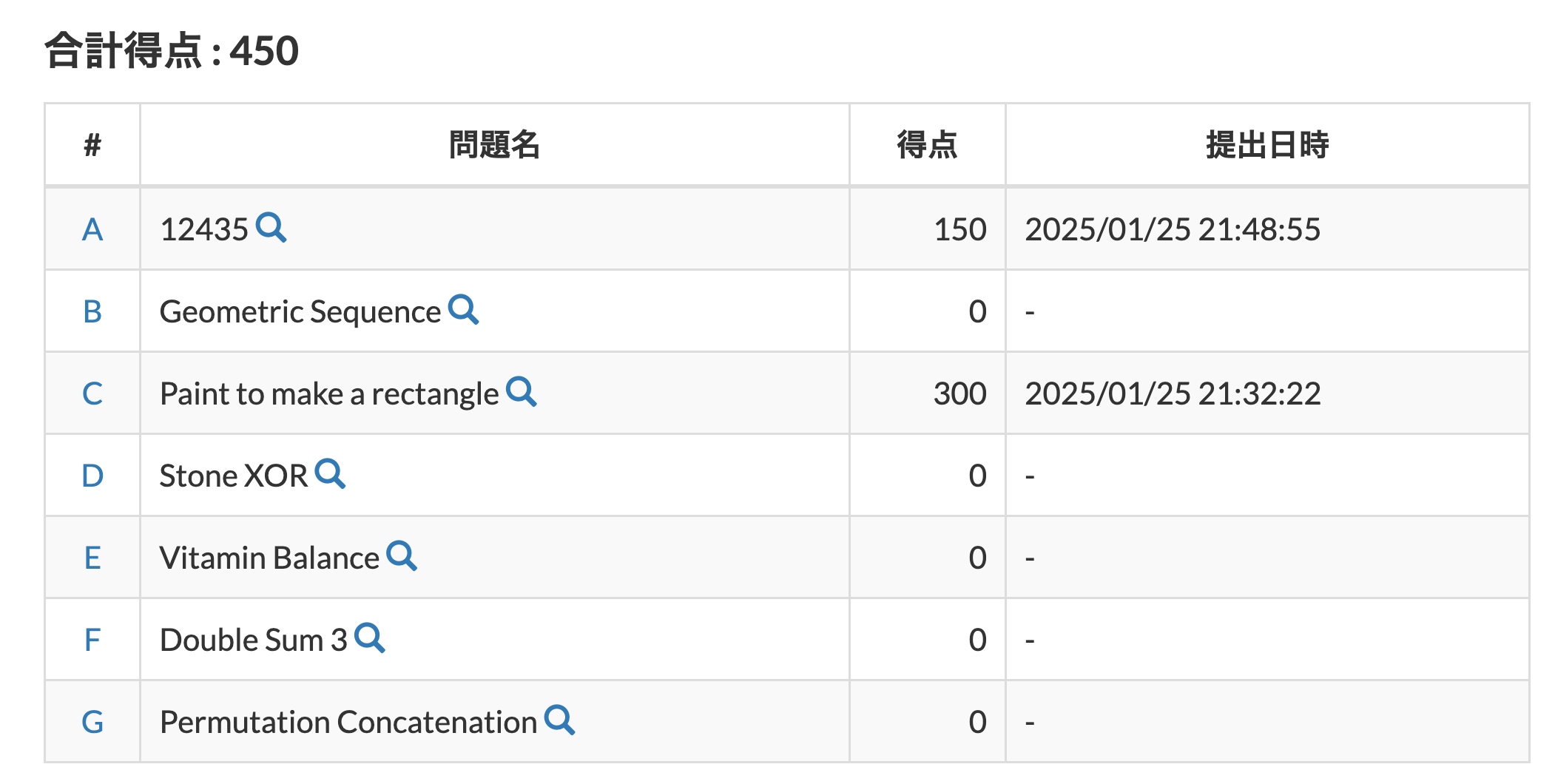
結果
ACの2完でした。rateの変動はなしです。
ふりかえり
A問題
- 問題
- 回答
現在の要素と次の要素を比較して、降順になっていたらカウントを1増やします。カウントが1以上の時に降順になっていたらFalseです。
main :: IO ()
main = do
as <- getInts
printYN $ f as
f = go 0
where
go cnt (a1 : a2 : t)
| cnt >= 1 && a1 > a2 = False
| a1 <= a2 = go cnt (a2 : t)
| a1 > a2 = go (cnt + 1) (a1 : t)
| otherwise = error "invalid pattern"
go 1 [a] = True
go 1 [] = True
go _ _ = False
B問題
- 問題
- 回答
まず、数字の配列が等比級数であること判定するために、今の値と次の値の間で商を取った配列を作りました。
zipWith (/) (tail as) as
この商をnubOrdで重複排除し、これが1つだけなら"Yes", そうでないなら"No"としました。
main :: IO ()
main = do
_ <- readLn @Int
as <- getDouble
let lst = nubOrd $ zipWith (/) (tail as) as
printYN $ length lst == 1
ですが、これだと除算で小数点以下の誤差が出てしまうので1ペナになってしまいます。
結局これが解決できずに解けなかったのですが、後で他の方のTLを見ていたところ2つ解法があることを知りました。
- 除算を避ける。等比級数なら現在の値、次の値、その次の値の比が同じなので、これを利用する
- Ratio型を利用する
1 については、A1, A2, A3, ..., Anが等比級数ならば、i番目の値をAiとすると、
Ai / Ai+1 = Ai+1 / Ai+2
となります。これはつまり、
Ai * Ai+2 = Ai+1 ^ 2
となります。これを再帰的に解いていけば、等比級数であることが判定できます。
Haskellで書くとこのような感じです。
isGeometric (x : y : z : ts) = x * z == y * y && isGeometric (y : z : ts)
isGeometric _ = True
2つ目の方法として、Ratio型を使う方法があります。
Ratio型は、内部的には以下の様に表現されていて、:%の左側が分子(numerator), 右側が分母(denominator)になります。
data Ratio a = !a :% !a deriving Eq
これを使うと、小数を使わず分数の形で数を扱うことができます。
実際に使ってみると、以下のような感じになります。
ghci> import Data.Ratio
ghci> 1 % 3
1 % 3
ghci> 3 % 1
3 % 1
約分も自動でやってくれます。
ghci> 2 % 4
1 % 2
ghci> 8 % 2
4 % 1
分母が0だともちろんエラーになります。
ghci> 1 % 0
*** Exception: Ratio has zero denominator
これを使用すると、Aの配列が全て自然数であることから、除算で小数点以下の計算をする必要がなくなるので誤差の心配をしなくてよくなります。
これでHaskellのコードを書くと、以下のような感じでACできました。
main :: IO ()
main = do
_ <- readLn @Int
as <- getInts
let len = length $ nubOrd $ zipWith (%) (tail as) as
printYN $ len == 1
C問題
- 問題
- 回答
まず、黒いマスが長方形であるための条件を考えます。
これは、最初のマス目に配置されている黒マスのうち
-
iの最小値、最大値を(minh, maxh) -
jの最小値、最大値を(minw, maxw)
とすると、
\begin{align}
minh \leq i \leq maxh \\
minw \leq j \leq maxh
\end{align}
となる(i, j)にある文字が全て# もしくは ?であれば良いことになります。
以上から、解法としては
-
'#'となる(i, j)を求める - 1で求めた
i,jのうち、最小、最大値をそれぞれ求める - 2で求めた
i, jの範囲の文字全てが'#'もしくは'?'であるかどうかを判定する
で解けることがわかります。
これをHaskellのコードに起こすと、以下の様になります。
main :: IO ()
main = do
[h, w] <- getInts
ss <- replicateM h getLine
let a = listArray @UArray ((1, 1), (h, w)) $ concat ss
idx = findArrayIndices (== '#') a
hs = sort $ map fst idx
ws = sort $ map snd idx
(minh, maxh) = (head hs, last hs)
(minw, maxw) = (head ws, last ws)
ans =
[v == '#' || v == '?' | i <- [minh .. maxh], j <- [minw .. maxw], let v = a ! (i, j)]
putStrLn $ if and ans then "Yes" else "No"
全体を振り返って
B問題は勉強になりました。大きい値で除算すると浮動小数点の誤差が無視できなくなるので、できるだけ除算しないようにするか、 Ratio型のような代替案を使うべきなのですね。
次回以降も今回学んだことを忘れない様にしっかり活かしたいとおもいます!