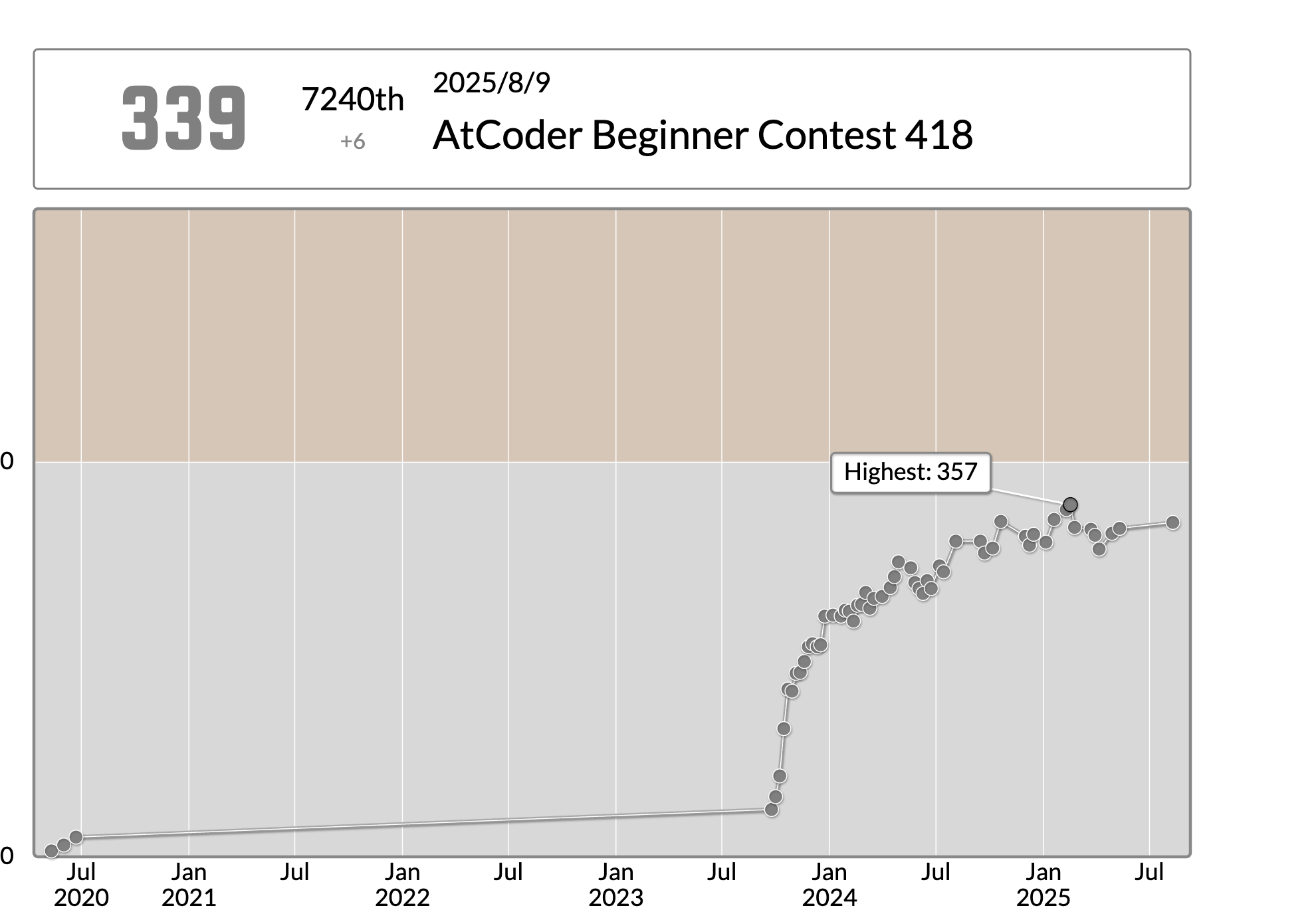
久しぶりのAtCoder Rated参加です
結果
今回はABの2完でした。
ふりかえり
A問題
- 問題
- 回答
末尾から3文字取って比較します
main :: IO ()
main = do
_ <- readLn @Int
s <- takeEnd 3 <$> getLine
printYn $ s == "tea"
B問題
- 問題
- 回答
部分文字列をすべて抽出して、先頭と末尾が両方tで長さが3以上のものを抽出します。
その後に充填率を計算して最大値を取ればよいです。
部分文字列をすべて抽出する関数を持っていなかったのでその場で作りました。
main :: IO ()
main = do
s <- getLine
let subs = substrings s
ans =
[ (x - 2) / (t - 2)
| s' <- subs,
let t = fromIntegral $ length s',
t >= 3.0,
head s' == 't' && last s' == 't',
let x = fromIntegral $ countBy (== 't') s'
]
print $ bool (maximum ans) 0.0 (null ans)
{-- lib --}
substring :: Int -> Int -> String -> String
substring start len str = take len (drop start str)
substringK :: Int -> String -> [String]
substringK k s = [substring i k s | i <- [0 .. length s - k]]
substrings :: String -> [String]
substrings s = concat [substringK i s | i <- [1 .. length s]]
C問題
- 問題
- 回答
プレイヤーが必ず勝つxを求める前に、ディーラーが勝つための最善の戦略を考えます。
ディーラーはできるだけ少ない個数を均等に配ろうとするので、可能な限り(b-1)個づつ配るのがディーラーが勝つための最善戦略になります。
よって、プレイヤー側が勝つためには、xに
可能な限り(b-1)個づつ配った場合の個数 + 1
を指定すれば良いことになります。
当然フレーバーの種類によってはAi < b-1となることもあるので、そのような場合はAi個配ることになります。
なので、ディーラーの配る最善策の個数は
Σmin(Ai, b-1)ということになります。
もう少し噛み砕くと
Ai < b - 1のとき ΣAi
Ai >= b - 1のとき Σ(b-1)
ということになります。つまり、答えは
(Ai < b - 1 となるAiのすべての個数) + (Ai > b - 1となるフレーバーの個数 x (b - 1)) + 1
になります。
(Ai < b - 1 となるAiのすべての個数)は毎回計算すると計算量が大きくなりTLEとなるため、事前に累積和を計算しておきましょう。
そうすると、さきほどの解は
(Ai < b - 1 となる最大のAiでの累積和) + (Ai > b - 1となるフレーバーの個数 x (b - 1)) + 1
となりますから、Ai < b - 1 となる最大のAiを二分探索で解いて計算すれば答えが得られます。自分はめんどうだったのでIntMapを作ってlookupLEで計算しました。
main :: IO ()
main = do
[n, q] <- getInts
ai <- sort <$> getInts
bs <- replicateM q $ readLn @Int
let sn = VU.fromList $ scanl' (+) 0 ai
im = IM.fromList $ zip ai [1 ..]
maxA = maximum ai
forM_ bs \b -> do
if b <= maxA
then do
let idx = snd $ fromMaybe 0 $ IM.lookupLE (b - 1) im
m = sn VU.! idx
l = (b - 1) * (n - idx)
print $ m + l + 1
else print (-1)
全体を振り返って
またぼちぼち頑張りますー